

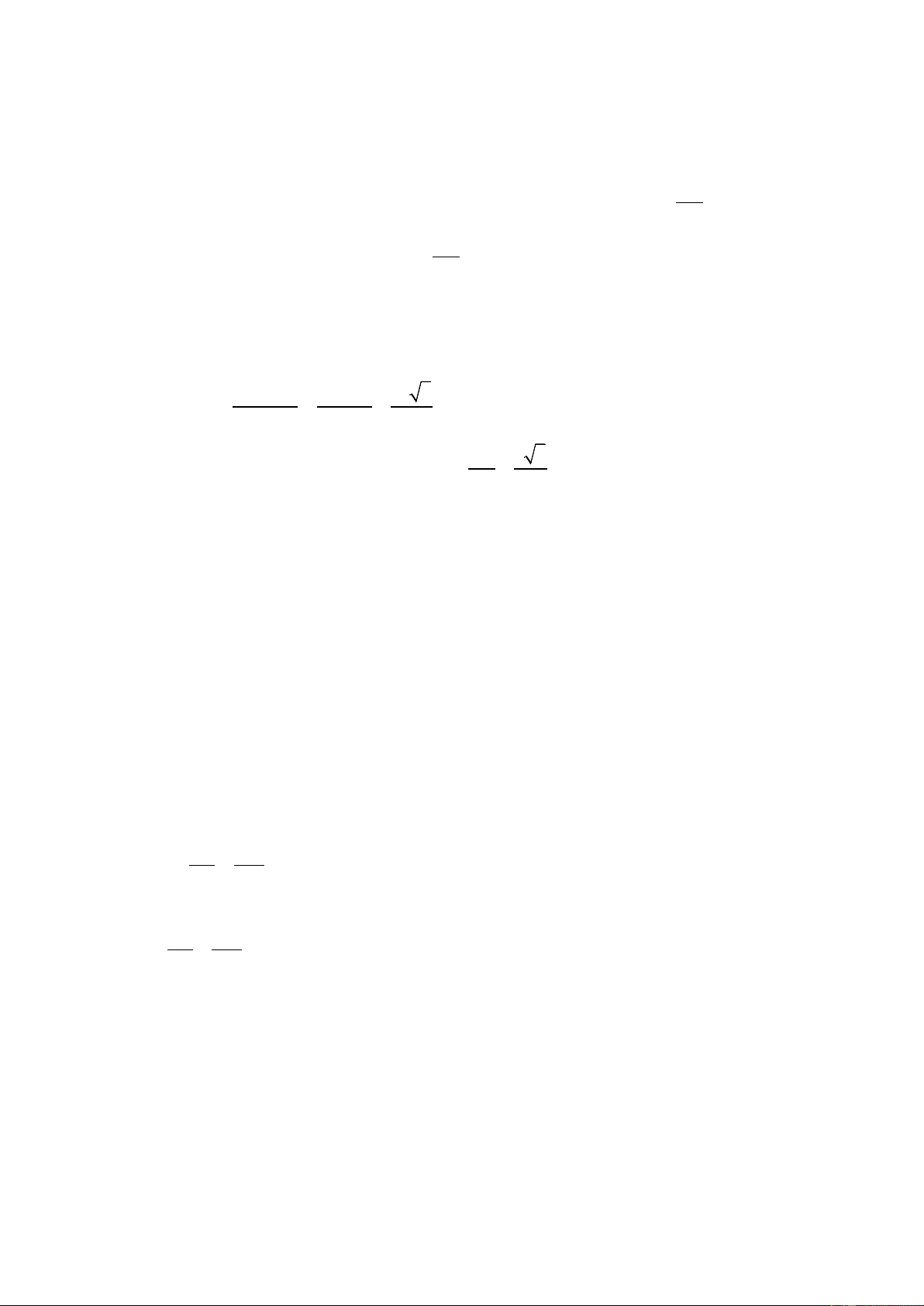


Preview text:
PHÒNG GD VÀ ĐT QUẬN CẦU GIẤY
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 THCS ARCHIMEDES ACADEMY NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề) 3 x −14 x + 3 2 x −1 Bài 1:
(2,5 điểm) Cho biểu thức A = − −
(với x ≥ 0 ; x ≠ 4 ; x ≠ 9 x − 5 x + 6 x − 2 3 − x ) x +1 a) Chứng minh A = x − 2
b) Tính A khi x = 7 − 4 3
c) Tìm x để A > 1 . 3 − 6 15 − 5 Bài 2:
(1,5 điểm) a) Tính: B = + . ( 5 + 3) 2 −1 3 −1
b) Giải phương trình sau: x − 4 x − 4 = 1. Bài 3:
(2,0 điểm) Cho hàm số y = (m + )
1 x + m + 2 (với tham số m ≠ 1
− ) có đồ thị là đường thẳng (d )
a) Tìm m để đồ thị hàm số đi qua điểm M ( 2; − − ) 1
b) Vẽ đồ thị hàm số ứng với giá trị m tìm được ở câu a trên hệ trục tọa độ Oxy và gọi
A , B lần lượt là giao điểm của đồ thị hàm số này với các trục Ox , Oy . Tính độ dài
đoạn AB và diện tích A ∆ . OB Bài 4:
(3,5 điểm) Cho đường tròn tâm O đường kính AB . Trên đoạn OB lấy điểm H sao cho
HB ≥ HO . Qua H kẻ dây CD vuông góc với AB . a) Nếu cho biết thêm
CAB = 30° và AC = 8 cm . Tính độ dài bán kính đường tròn (O) và
độ dài dây CD (giả thiết thêm này chỉ dùng riêng cho câu a không dùng để làm những câu còn lại).
b) Lấy điểm I nằm trong tam giác ACH sao cho BI = BC . Chứng minh 2
BI = BH.BA và BIH = BAI .
c) Gọi giao điểm của AI và CH là K . Qua I kẻ đường thẳng vuông góc với AK ,
đường thẳng này cắt đường thẳng CD tại P . Giả sử BK song song với IH . Khi đó: 1) Chứng minh: 2
KB = KI.KA = KH.KP và KBP = 90°
2) Chứng minh: OI = OH Bài 5:
(0,5 điểm) Cho các số thực a, ,
b c ≥ 1 thỏa mãn ab + bc + ca = 4 . Tìm giá trị lớn nhất
của biểu thức P = 5a + 4b + c . HẾT
HƯỚNG DẪN GIẢI CHI TIẾT x +1 Bài 1: a) Chứng minh A = x − 2 Ta có: 3 x −14 x + 3 2 x −1 A = − − x − 5 x + 6 x − 2 3 − x 3 x −14 x + 3 2 x −1 = ( − +
x − 2)( x − 3) x − 2 x − 3
3 x −14 − ( x + 3)( x − 3) + (2 x − ) 1 ( x − 2) =
( x −2)( x −3)
3 x −14 − ( x − 9) + (2x − 5 x + 2) =
( x −2)( x −3)
3 x −14 − x + 9 + 2x − 5 x + 2 =
( x −2)( x −3) x − 2 x − 3
= ( x −2)( x −3)
( x + )1( x −3)
= ( x −2)( x −3) x +1 = x −2 x +1 Vậy A =
với x ≥ 0 ; x ≠ 4 ; x ≠ 9 . x − 2
b) Với x = 7 − 4 3 (thỏa mãn điều kiện) Ta có x = ( − )2 2 3 ⇒ x = 2 − 3
Thay vào biểu thức A ta được: 2 − 3 +1 3 − 3 A = = = 1− 3 2 − 3 − 2 − 3
Vậy với x = 7 − 4 3 thì A = 1− 3 c) Ta có A > 1 x +1 ⇒ >1 x − 2 x +1 ⇒ −1 > 0 x − 2 x +1− x + 2 ⇒ > 0 x − 2 3 ⇒ > 0 x − 2 Vì 3 > 0 ⇒ x − 2 > 0 ⇒ x > 4
Kết hợp với điều kiện xác định x ≥ 0 ; x ≠ 4 ; x ≠ 9 .
⇒ x > 4 , x ≠ 9 thì A > 1 3 − 6 15 − 5 Bài 2: a) B = + . ( 5 + 3) 2 −1 3 −1 3(1− 2) 5( 3 − )1 = + .( 5 + 3) 2 −1 3 −1 = (− 3 + 5)( 5 + 3) = ( 5 − 3)( 5 + 3) = 5 − 3 = 2
b) x − 4 x − 4 = 1 (Điều kiện x ≥ 4 )
⇔ (x − 4) − 4 x − 4 + 4 =1 ⇔ ( x − − )2 4 2 = 1 ⇔ x − 4 − 2 = 1 x − 4 − 2 =1 ( )1 ⇔
x − 4 − 2 = 1 − (2) Giải ( ) 1 ⇒ x − 4 = 3
⇔ x = 13 (Thỏa mãn điều kiện)
Giải (2) ⇒ x − 4 = 1
⇔ x = 5 (Thỏa mãn điều kiện)
Vậy tập hợp nghiệm của phương trình là S = {13; } 5 . Bài 3:
a) Để đồ thị hàm số đi qua điểm M ( 2; − − ) 1 ⇔ M ( 2; − − ) 1 ∈ (d ) nên 1 − = (m + ) 1 .( 2
− ) + m + 2 ⇔ −m = 1
− ⇔ m = 1 (thỏa mãn điều kiện)
Vậy đồ thị hàm số đi qua điểm M ( 2; − − )
1 khi và chỉ khi m = 1
b) Với m = 1 ta được hàm số y = 2x + 3 .
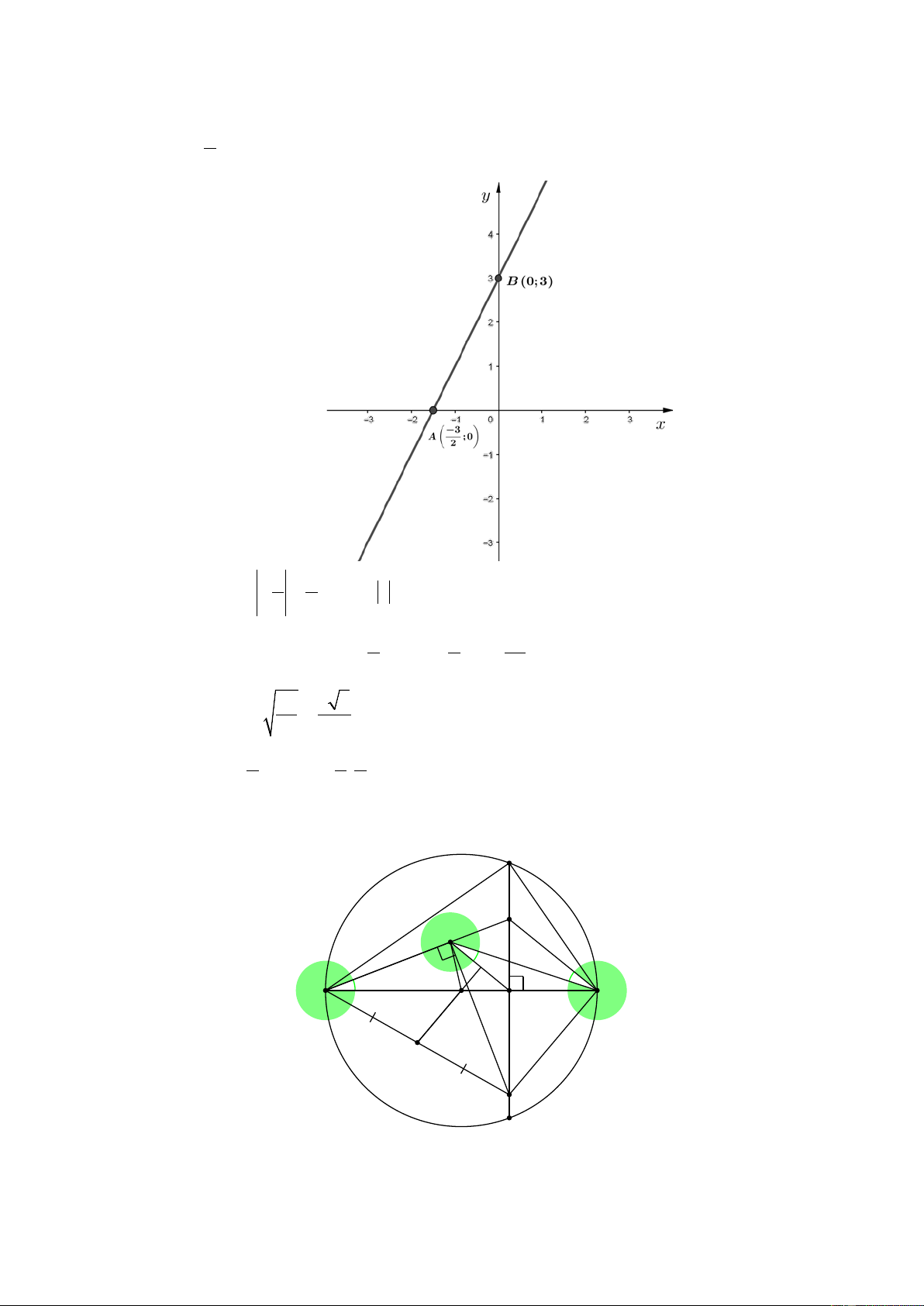
Đồ thị hàm số y = 2x + 3, cắt trục tung Oy tại B(0;3) và cắt trục hoành Ox tại 3 A − ; 0
. Do đó, hàm số có đồ thị là đường thẳng đi qua hai điểm A và B . 2 3 3 Ta có OA = −
= ; OB = 3 = 3. Xét A
∆ BO vuông tại O nên áp dụng định lý Pytago 2 2 2 3 9 45 ta có 2 2 2 2
AB = OA + OB = + 3 = + 9 = 2 4 4 45 3 5 Suy ra AB = = (đơn vị độ dài). 4 2 1 1 3 Và S = . . OA OB =
. .3 = 2, 25 (đơn vị diện tích). ABO 2 2 2 Bài 4: C K I A B O H M P D a) Nếu cho biết thêm
CAB = 30° và AC = 8 cm . Tính độ dài bán kính đường tròn (O) và
độ dài dây CD (giả thiết thêm này chỉ dùng riêng cho câu a không dùng để làm những câu còn lại). AB
Vì C thuộc đường tròn tâm O đường kính AB ⇒ OA = OB = OC = = R 2 AB Xét A
∆ CB ta có: OA = OB = OC = = R 2 ⇒ A
∆ CB vuông tại C Xét A
∆ CB vuông tại C , ta có: AC = A . B cos CAB AC 8 16 3 ⇒ AB = = = (cm) cos CAB cos 30° 3 ⇒ Độ AB 8 3
dài bán kính đường tròn (O) là: = (cm) 2 3 Xét A
∆ CH vuông tại H , ta có:
CH = AC.sin CAH = AC.sin CAB = 8.sin 30° = 4 (cm)
Xét (O) có: AB là đường kính, CD là dây cung, AB ⊥ CD tại H (giả thiết) ⇒ H là
trung điểm của CD (quan hệ giữa đường kính và dây cung) ⇒ CD = 2CH = 2.4 = 8(cm) .
b) Lấy điểm I nằm trong tam giác ACH sao cho BI = BC . Chứng minh 2
BI = BH.BA và BIH = BAI . +) Xét A
∆ CB vuông tại C , đường cao CH ta có: 2
BC = BH.BA (quan hệ giữa cạnh và đường cao tam giác vuông)
Mà BI = BC (giả thiết) Do đó, suy ra 2
BI = BH.BA (điều phải chứng minh). BI BH ⇒ = BA BI Xét B ∆ IH và B ∆ AI , ta có: BI
BH (chöùng minh treân) = BA BI ⇒ B ∆ IH ∽ B
∆ AI (c – g – c) ABI chung
⇒ BIH = BAI (điều phải chứng minh) ( ) 1
c) Gọi giao điểm của AI và CH là K . Qua I kẻ đường thẳng vuông góc với AK ,
đường thẳng này cắt đường thẳng CD tại P . Giả sử BK song song với IH . Khi đó: 1) Chứng minh: 2
KB = KI.KA = KH.KP và KBP = 90°
Vì BK // IH (giả thiết)
⇒ BIH = IBK (hai góc so le trong) (2) Từ ( ) 1 và (2)
⇒ BAI = IBK hay BAK = IBK Xét K ∆ BI và K ∆ AB , ta có:
BAK = IBK (chöùng minh treân)⇒ K ∆ BI ∽ K ∆ AB (g – g) AKB chung KB KI 2 ⇒ =
⇒ KB = KI.KA (3) KA KB Xét K ∆ IP và K ∆ HA , ta có:
KIP = KHA(= 90°)⇒ KI ∆ P ∽ KH ∆ A (g – g) K chung KI KP ⇒ =
⇒ KI.KA = KH.KP (4) KH KA Từ (3) và (4) 2
⇒ KB = KI.KA = KH.KP (điều phải chứng minh). KB KP ⇒ = KH KB Xét K ∆ BH và K ∆ PB , ta có: KB
KP (chöùng minh treân) = KH KB ⇒ K ∆ BH ∽ K
∆ PB (c – g – c) PKB chung
⇒ KHB = KBP ; mà KHB = 90°
⇒ KBP = 90° (điều phải chứng minh).
2) Chứng minh: OI = OH
Gọi M là trung điểm của AP Xét A ∆ PB , ta có: AM = MP
⇒ OM là đường trung bình của A ∆ PB .
OA = OB = R ⇒ OM // BP
Mà BP ⊥ BK (vì KBP = 90° )
⇒ OM ⊥ BK (từ vuông góc đến song song)
Hay OM ⊥ IH (vì IH // BK ) (*) Xét A
∆ HP vuông tại H , ta có: AP
MH = AM = MP =
(tính chất trung tuyến và cạnh huyền tam giác vuông) (5) 2 Xét A
∆ IP vuông tại I , ta có: AP
MI = AM = MP =
(tính chất trung tuyến và cạnh huyền tam giác vuông) (6) 2
Từ (5) và (6) ⇒ MH = MI
⇒ M thuộc trung trực của IH (tính chất đường trung trực của đoạn thẳng) (**)
Từ (*) và (**) ⇒ MO là đường trung trực của IH .
⇒ OI = OH (điều phải chứng minh). 1 − a ≤ 0 (
1− a)(1− b) ≥ 0 1
+ ab ≥ a + b Bài 5:
Do a, b, c ≥ 1 ⇒ 1 − b ≤ 0 ⇒ (
1− b)(1− c) ≥ 0 ⇒ 1
+ bc ≥ b + c 1− c ≤ 0 (1− a )(1−c) ≥ 0
1+ ca ≥ c + a
⇒ 3 + ab + bc + ca ≥ 2(a + b + 7
c) ⇒ a + b + c ≤ . 2
Dấu “=” xảy ra khi 2 số bằng 1. Do ,
b c ≥ 1 ⇒ b + 4c ≥ 5 ⇒ − (b + 4c) ≤ 5 −
Ta có: P = 5a + 4b + c = 5.(a + b + c) − (b + 4c)
Suy ra P ≤ (a + b + c) 7 25 5 − 5 = 5. − 5 = . 2 2 b = c = 1 25 Vậy P = khi . max 3 2 a = 2 HẾT




