PHÒNG GD VÀ ĐT THANH OAI
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
TRƯỜNG THCS CAO DƯƠNG NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề) Câu 1:
(2điểm) Thực hiện các phép tính.
a) 7 5 + 3 20 − 125 − 2 45 . b) 144 − 25. 4 . 2 2 c) ( − )2 3 1 2 − 64 − 2 . d) + . 5 + 2 5 − 2 Câu 2:
(2 điểm)Giải các phương trình sau. a) 2x +1 = 5 b) x − 2 = 2x − 7
c) x + 3 x − 4 = 0 d) 2 x − 2x +1 = 3 Câu 3:
(2 điểm)Cho hai biểu thức x +1 x 3 4 − 6 x A = và B = + +
với x ≥ 0 ; x ≠ 1 x + 5 x −1 x +1 x −1
a) Tính giá trị của biểu thức A khi x = 16
b) Rút gọn biểu thức B
c) Tìm giá trị nhỏ nhất của biểu thức S = . A B Câu 4:
(3 điểm)Cho tam giác ABC vuông tại A .
a) Giả sử khi AB = 9cm ; AC = 12cm . Tính cạnh BC và các góc còn lại của tam giác
ABC (làm tròn đến độ).
b) Gọi H là hình chiếu của A trên BC ; E , F lần lượt là hình chiếu của H trên AB , AC . Tính EF .
c) Chứng minh rằng: AE.AB = AF.AC .
d) Gọi K là trung điểm của BC , biết AK cắt EF tại I . Chứng tỏ rằng AK vuông góc với EF . Câu 5: (0,5 điểm).
Giải phương trình sau: 1 x − 2000 + y − 2001 + z − 2002 =
(x + y + z)−3000 . 2 HẾT
PHÒNG GD VÀ ĐT THANH OAI
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
TRƯỜNG THCS CAO DƯƠNG NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: a) 7 5 + 3 20 − 125 − 2 45 b) 144 − 25. 4 = 7 5 + 6 5 − 5 5 − 6 5 = 12 − 5.2 = = 2 5 . 2 . 2 2 c) ( − )2 3 1 2 − 64 − 2 d) + 5 + 2 5 − 2 = 2 −1− 4 − 2 2 ( 5 − 2) 2 ( 5 + 2) = 5 − . = ( +
5 + 2)( 5 − 2) ( 5 + 2)( 5 − 2) 2 5 − 4 + 2 5 + 4 = 1 = 4 5 . − Câu 2: a) 2x +1 = 5 . ĐK 1 x ≥ 2 ⇔ 2x +1 = 25 ⇔ x = 12(TM ) Vậy S = { } 12 b) x − 2 = 2x − 7 . ĐK 7 x ≥ 2
⇔ x − 2 = 2x − 7 ⇔ x = 5(TM ) Vậy S = { } 5
c) x + 3 x − 4 = 0 , x ≥ 0
⇔ x + 4 x − x − 4 = 0
⇔ ( x + 4)( x −1) = 0 ⇔ ( x − ) 1 = 0
⇔ x = 0 ⇔ x = 1(TM ) Vậy S = { } 1 d) 2 x − 2x +1 = 3 2 ⇔ (x −1) = 3 ⇔ x −1 = 3 x −1 = 3 x = 4 ⇔ ⇔   x −1 = 3 − x = 2 − Vậy S = {4; − } 2 Câu 3:
a) Thay x = 16 vào biểu thức A 16 +1 5 A = = 16 + 5 9 x 3 4 − 6 x b) B = + + x −1 x +1 x −1 x ( x + ) 1 x ( x − ) 1 4 − 6 = x B ( x ) + + −1 ( x + ) 1
( x − )1( x + )1 ( x − )1( x + )1 x +
x + 3 x − 3 + 4 − 6 = x B
( x − )1( x + )1 x − 2 x +1
B = ( x − )1( x + )1 ( x − )2 1 x −1 B = ( x − ) = 1 ( x + ) 1 x +1 x +1 x −1 x −1 6 − c) S = . A B = . = = 1+ x + 5 x +1 x + 5 x + 5 Có x ≥ 0 ⇔ x ≥ 0 ⇔ x + 5 ≥ 5 6 − 6 − ⇔ ≥ x + 5 5 6 − 6 − ⇔ 1+ ≥ 1+ x + 5 5 1 − ⇒ S ≥ 5
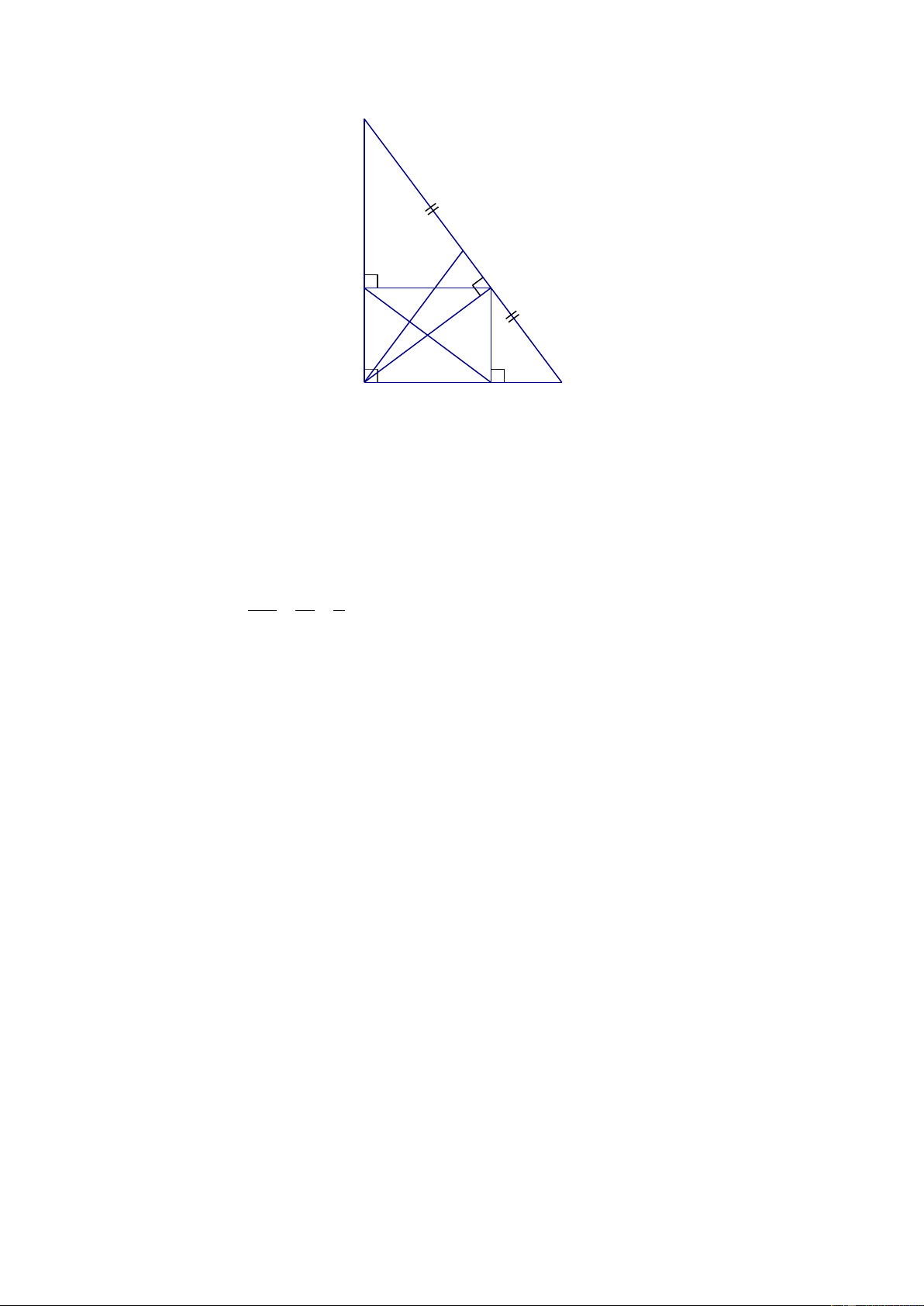
Xảy ra dấu bằng khi x = 0 . 1 − Vậy GTNN S = khi x = 0 . 5 Câu 4: C K H F 1 I 1 1 A E B a) Xét A
∆ BC vuông tại A có: 2 2 2
AB + AC = BC (Định lí Pytago) 2 2 2 ⇔ 9 +12 = BC 2 ⇔ BC = 225 ⇔ BC = 15cm .  AC 12 4 sin ABC = = = BC 15 5 ⇒  ABC ≈ 53° Mà  ABC + 
ACB = 90° (Định lí) ⇒ 
ACB ≈ 90° − 53° ≈ 37°
b) Xét tứ giác AEHF có:  AEH =  EAF =  AFH = 90°
⇒ Tứ giác AEHF là hình chữ nhật.
⇒ AH = EF (tính chất) Xét A
∆ BC vuông tại A , đường cao AH có:
AH .BC = A .
B AC (hệ thức lượng) ⇔ AH.15 = 9.12 ⇔ AH = 7,2cm ⇒ EF = 7,2cm c) Xét A
∆ BH vuông tại H , đường cao HE có: 2
AE.AB = AH (hệ thức lượng) ( )1 Xét A
∆ CH vuông tại H , đường cao HF có: 2
AF.AC = AH (hệ thức lượng) (2) Từ ( )
1 và (2) ta có AE.AB = AF.AC (đpcm)
d) Ta có: AE.AB = AF.AC (cmt) AE AC ⇒ = AF AB Xét A ∆ EF và A ∆ CB có:  EAF chung AE AC = (cmt) AF AB
⇒ ∆ AEF” ∆ACB (c.g.c) ⇒  =  F
B (2 góc tương ứng) 1 Xét A
∆ BC vuông tại A có AK là đường trung tuyến
⇒ AK = KC (tính chất) ⇒ A
∆ KC cân tại K ⇒  =  A C (tính chất) 1 Mà  B +  C = 90° (định lí) ⇒  A +  F = 90° 1 1 Xét A ∆ IF có:  A +  F + 
I = 90° (định lí tổng 3 góc trong một tam giác) 1 1 1 ⇒ I = 90° 1 ⇒ AK ⊥ EF 1 Câu 5: x − 2000 + y − 2001 + z − 2002 =
(x + y + z)−3000 (*) . (Điều kiện: x ≥ 2000 , 2
y ≥ 2001 , z ≥ 2002 ). x − 2000 ≥ 0 
Do x ≥ 2000 , y ≥ 2001 , z ≥ 2002 nên suy ra:  y − 2001 ≥ 0 . z − 2002 ≥ 0 
Áp dụng bất đẳng thức Cô – si cho hai số không âm ta được:
(x − 2000)+1≥ 2 (x − 2000).1 ⇔ x −1999 ≥ 2 x − 2000 ( )1 . ( y − ) 2001 +1 ≥ 2 ( y − )
2001 .1 ⇔ y − 2000 ≥ 2 y − 2001 (2) .
(z − 2002)+1≥ 2 (z − 2002).1 ⇔ z − 2001≥ 2 z − 2002 (3).
Cộng vế với vế của ( ) 1 , (2) , (3) ta được:
x + y + z − 6000 ≥ 2 x − 2000 + 2 y − 2001 + 2 z − 2002 1
⇔ (x + y + z) −3000 ≥ x − 2000 + y − 2001 + z − 2002 (4) . 2 
x = 2001 (TM ) x − 2000 = 1  
Dấu " = " xảy ra khi và chỉ khi  y − 2001 = 1 ⇔  y = 2002 (TM ) (**) .   z − 2002 = 1  z = 2003  (TM )
x = 2001 (TM ) 
Từ (*) , (4) và (**) suy ra (*) ⇔  y = 2002 (TM ) . z = 2003  (TM )
Vậy phương trình (*) có nghiệm là: ( x; y ; z) = (2001; 2002; 2003) .
__________ THCS.TOANMATH.com __________