Đề thi giữa kì 1 Toán 9 năm 2020 – 2021 trường THCS Cầu Giấy – Hà Nội

Đề thi giữa kì 1 Toán 9 năm 2020 – 2021 trường THCS Cầu Giấy – Hà Nội được biên soạn theo hình thức đề thi tự luận, đề gồm 05 câu, thời gian làm bài 90 phút, đề thi có đáp án và lời giải chi tiết. Mời bạn đón xem.

33 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 9

Môn: Toán 9

Thông tin:

6 trang 9 tháng trước

Tác giả:

Profile Hà Việt Anh
Bài 1: (2 điểm) Tính giá trị biểu thức
( )
26 43 52.36= −+A
23 23
23 23
−+
= +
+−
B
48 10 7 4 3 2 3= − + ++C
Bài 2: (1,5 điểm) Giải các phương trình sau
a)
3 40− −=xx
b)
2 1 15−+ −=xx
c)
( )
( )
22
2 7 3 1. 3+ += + +xx x x
Bài 3: (2,5 điểm) Cho biểu thức:
7
1
x
A
x
+
=
−
và
13 8
21 2
x
B
x xx x
+
= ++
+ − +−
với
,
1x ≠
a) Tính giá trị của
A
biết
9 42x = +
b) Rút gọn
B
c) Tìm các giá trị nguyên của
x
để biểu thức
.P AB=
có giá trị nguyên
Bài 4: (3,5 điểm)
1. Một cột đèn có bóng trên mặt đất dài
8,5m
. Các tia nắng mặt trời tạo với mặt đất một góc
xấp xỉ
38°
. Tính chiều cao của cột đèn ? (Kết quả làm tròn đến 1 chữ số thập phân)
2. Cho
ABC∆
nhọn có
60ABC = °
, đường cao
AH
. Đường thẳng qua
C
vuông góc với
AC
cắt đường thẳng
AH
tại
D
. Gọi
E
và
F
lần lượt là hình chiếu của
H
trên
AC
và
CD
.
a) Nếu
3cmAH =
,
5cmAC =
. Tính độ dài các đoạn thẳng
HC
,
HD
,
CD
?
b) Chứng minh rằng
..CF CD CE CA=
.
c) Biết
8cmAB BC+=
, tìm giá trị lớn nhất của diện tích tam giác
ABC
.
Bài 5: (0,5 điểm) Cho
,,abc
là các số thực dương thỏa mãn:
ab bc ca abc++=
. Tìm giá trị lớn nhất
của biểu thức:
( ) ( ) ( )
111
abc
P
bc a ca b ab c
=++
+++
.
HẾT
PHÒNG GD&ĐT QUẬN CẦU GIẤY
T
RƯỜNG THCS CẦU GIẤY
----------
THCS.TOANMATH.com
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
NĂM HỌC 2020 - 2021
MÔN TOÁN - LỚP 9
Th
ời gian làm bài: 90 phút (không kể thời gian phát đề)
HƯỚNG DẪN GIẢI CHI TIẾT
Bài 1:
( )
26 43 52.36= −+A
2 6.3 6 4 3.3 6 5 2.3 6=−+A
36 12 18 15 12=−+A
22
36 12 3 .2 15 2 .3=−+A
36 12.3 2 15.2 3 36 36 2 30 3=− + =−+A
23 23
23 23
−+
= +
+−
B
( )
( )
( )
( )
( )
( )
22
23 23
2 3.2 3 2 3.2 3
−+
= +
+− −+
B
( ) ( )
22
23 23=− ++B
2 32 3=− ++B
2 32 34=− ++ =B
48 10 7 4 3 2 3= − + ++C
( )
2
48 10 2 3 2 3= − + ++C
48 10. 2 3 2 3= − + ++C
48 20 10 3 2 3= − − ++C
28 10 3 2 3= − ++C
( )
2
53 23= − ++C
532353237= − ++ =− ++ =C
Bài 2:
a)
3 40− −=xx
(điều kiện:
0≥x
)
⇔
4 40+ − −=xx x
⇔
( )
( )
4 40+ − +=xx x
⇔
( )
( )
. 14 10+− +=xx x
⇔
( ) ( )
4. 1 0− +=xx
⇔
40−=x
(do
10+>x
với mọi
0x ≥
)
⇔
4=x
⇔
16=x
(thỏa mãn điều kiện)
Vậy phương trình có nghiệm
16=x
b)
2 1 15−+ −=xx
(điều kiện:
1≥x
)
⇔
( )
2
2
21 1 5−+ − =xx
⇔
( ) ( )
2 1 1 2. 2 1 . 1 25−+ −+ − − =xx x x
⇔
2
3 2 2. 2 3 1 25−+ − +=x xx
⇔
2
2. 2 3 1 27 3− += −xx x
(điều kiện:
9≤x
)
⇔
22
8 12 4 9 162 729− += − +xx x x
⇔
2
150 725 0− +=xx
⇔
2
5 145 725 0−− + =xx x
⇔
( ) ( )
5 . 145 0− −=xx
⇔
50−=x
(do đk
9x ≤
nên
145 0−<x
)
⇔
5=x
(thỏa mãn điều kiện
19≤≤x
)
Vậy phương trình có nghiệm
5=x
c)
( )
( )
22
2 7 3 1. 3+ += + +xx x x
(điều kiện:
3≥−x
)
⇔
( )
( )
( )
( )
22
2 3 3 1. 3 01 + +− ++ +=x x xx
⇔
( ) ( )
( )
( )
( )
( )
22 2
1. 3 2 3 1. 3 01 −++ ++ + − + +=x xx x xx
⇔
(
)
(
)
22 2
2 3 3 10113+++ +− + +− + =xx x xx x
⇔
(
)
(
)
22
23 01 .13+ +− +−+ =x xxx
Trường hợp 1:
2
2 301 − +=+xx
2
12 3
xx⇔ += +
2
1 4 12xx⇔ += +
2
4 11 0xx⇔ − −=
Ta có
2
4 11 0xx⇔ − −=
2
4 11xx⇔−=
( )
2
2
4 4 15 2 15xx x⇔ − += ⇔ − =
⇔
2 15= ±x
(thỏa mãn điều kiện)
Trường hợp 2:
2
301 − +=+xx
⇔
2
13+= +xx
⇔
2
13+= +xx
⇔
2
20−−=xx
⇔
( ) ( )
2. 1 0− +=xx
⇔
1= −x
hoặc
2=x
(thỏa mãn điều kiện)
Kết hợp với điều kiện ta được phương trình có tập nghiệm
{ }
2 15; 1;2;2 15=−−+S
.
Bài 3:
a) Ta có:
( )
2
9 4 2 8 2.2 2.1 1 2 2 1x =+ =+ += +
(thoả mãn điều kiện)
( )
2
22 1 22 1x⇒= += +
, thay vào biểu thức
A
, ta có:
( )
22.22 1
22 17 22 8
22 1
22 11 22 22
A
+
++ +
= = = = +
+−
Vậy
9 42x = +
, thì
22 1A = +
b) Với
0x ≥
,
1x ≠
ta có:
13 8
21 2
x
B
x xx x
+
= ++
+ − +−
( )
( )
8
21
13
21x
x
x
x
x +
=
−
+
−
+
−
+
( )
( )
( )
( )
( )
( )
( )
2
21
3
18
1 21 2xx x
x
x
x
x
xx
+
=
+− +−
−+
−+
+−
( )
( )
( )
21
13 2 8
xx
x xx−− + +
+
+
−
=
( )
( )
21
13 6 8
xx
x xx−− − +
+
+
−
=
( )
( )
1
21
2
x
x
x
x
=
+
+
−
−
( )
( )
( )
2
21
1
x
x
x
−
+−
=
2
1x
x
−
=
+
c) Ta có:
71 7 5
.. 1
12 2 2
xx x
P AB
xx x x
+− +
= = = = +
−+ + +
Ta có:
, để
P∈
5
2x
⇒∈
+
52x⇒+
( ) { }
2 5 2 1; 5Öxx⇒ +∈ ⇒ +∈±±
Mà
22x +≥
với
0x ≥
,
1x ≠
Do đó:
25 3xx+=⇒ =
9x⇒=
(thoả mãn)
Vậy
9x =
thì
.P AB=
có giá trị nguyên.
Bài 4:
a) Nếu
3cmAH =
,
5cmAC =
. Tính độ dài các đoạn thẳng
HC
,
HD
,
CD
?
+) Xét
AHC∆
vuông tại
H
, đường cao
HE
ta có:
222
AH HC AC+=
(định lý Py-ta-go)
22222
5 3 25 9 16HC AC AH⇒=−=−=−=
4HC⇒=
(cm)
2
.HC CE AC=
(quan hệ giữa cạnh và đường cao tam giác vuông)
22
4 16
3, 2
55
HC
CE
AC
⇒= ===
(cm)
+) Xét tứ giác
HECF
có:
90HEC ECF HFC= = = °
⇒
tứ giác
HECF
là hình chữ nhật (dấu hiệu nhận biết)
3, 2HF CE⇒==
(cm)
+) Xét
CHD∆
vuông tại
H
, đường cao
HF
ta có:
2 22
111
HF HC HD
= +
(quan hệ giữa cạnh và đường cao tam giác vuông)
2 22
111
HD HF HC
⇒=−
( )
( )
2
2
22
2
2
22
2
4 . 3, 2
. 256
9
4 3, 2
HC HF
HD
HC HF
⇒= = =
−
−
256 16
5,3
93
HD⇒= =≈
(cm)
Có:
..HF CD HC HD=
(quan hệ giữa cạnh và đường cao tam giác vuông)
16
4.
. 20
3
6,7
16
3
5
HC HD
CD
HF
⇒= = =≈
(cm)
b) Chứng minh rằng
..CF CD CE CA=
.
60
°
F
E
D
H
B
C
A
+) Xét
AHC∆
vuông tại
H
, đường cao
HE
ta có:
2
.HC CE AC=
(quan hệ giữa cạnh và đường cao tam giác vuông)
( )
1
+) Xét
CHD∆
vuông tại
H
, đường cao
HF
ta có:
2
.HC CF CD=
(quan hệ giữa cạnh và đường cao tam giác vuông)
( )
2
Từ
( )
1
và
( )
2
..CF CD CE CA⇒=
(điều phải chứng minh)
c) Biết
8cmAB BC+=
, tìm giá trị lớn nhất của diện tích tam giác
ABC
.
Ta có:
1
.
2
ABC
S AH BC=
Vì
ABH∆
vuông tại
H
nên ta có
.sinAH AB B=
Do đó:
1 1 13 3
. .sin . .sin60 . . . .
2 2 22 4
ABC
S AB BC B AB BC AB BC AB BC= = °= =
Mặt khác
22
8
. 16
22
AB BC
AB BC
+

≤==


Dấu “=” xảy ra khi
4cmAB BC= =
Do đó:
( )
2
3
.16 4 3
4
cm
ABC
S
∆
≤=
Vậy
2
max 4 3 cm
ABC
S
∆
=
khi
ABC∆
cân tại
B
.
Bài 5: Ta có:
( ) ( ) ( ) ( )
( )
1
14
a a a a aa
bc a abc bc ab bc ca bc b a c c a b b a c c a b

== = ≤+


+ + +++ ++ + + +

Tương tự ta chứng minh được:
( )
( )
( )
1
4
b bb
acba abc cab

≤+


+ ++

( ) ( ) ( )
1
14
c cc
abc ba c ab c

≤+


+ ++

Do đó
( ) ( ) ( )
( ) ( ) ( )
1
1 1 14
a b c ac bc ab
P
bca cab abc ba c ab c ca b

+++
= + + ≤ ++


+ + + +++

11 1 1 1 1
.
44 4
ab bc ca
P
a b c abc
++

⇔ ≤ ++ = =


1
max
4
P⇒=
Dấu bằng xảy ra khi
( ) ( ) ( )
b a c c a b a b c ab bc ac bc ab ac+= += +⇔ +=+= +
abc ac abc ab abc bc⇔ −= −= −
.
ab bc ca⇔==
mà
3ab bc ca abc a b c+ + = ⇔===
HẾT
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

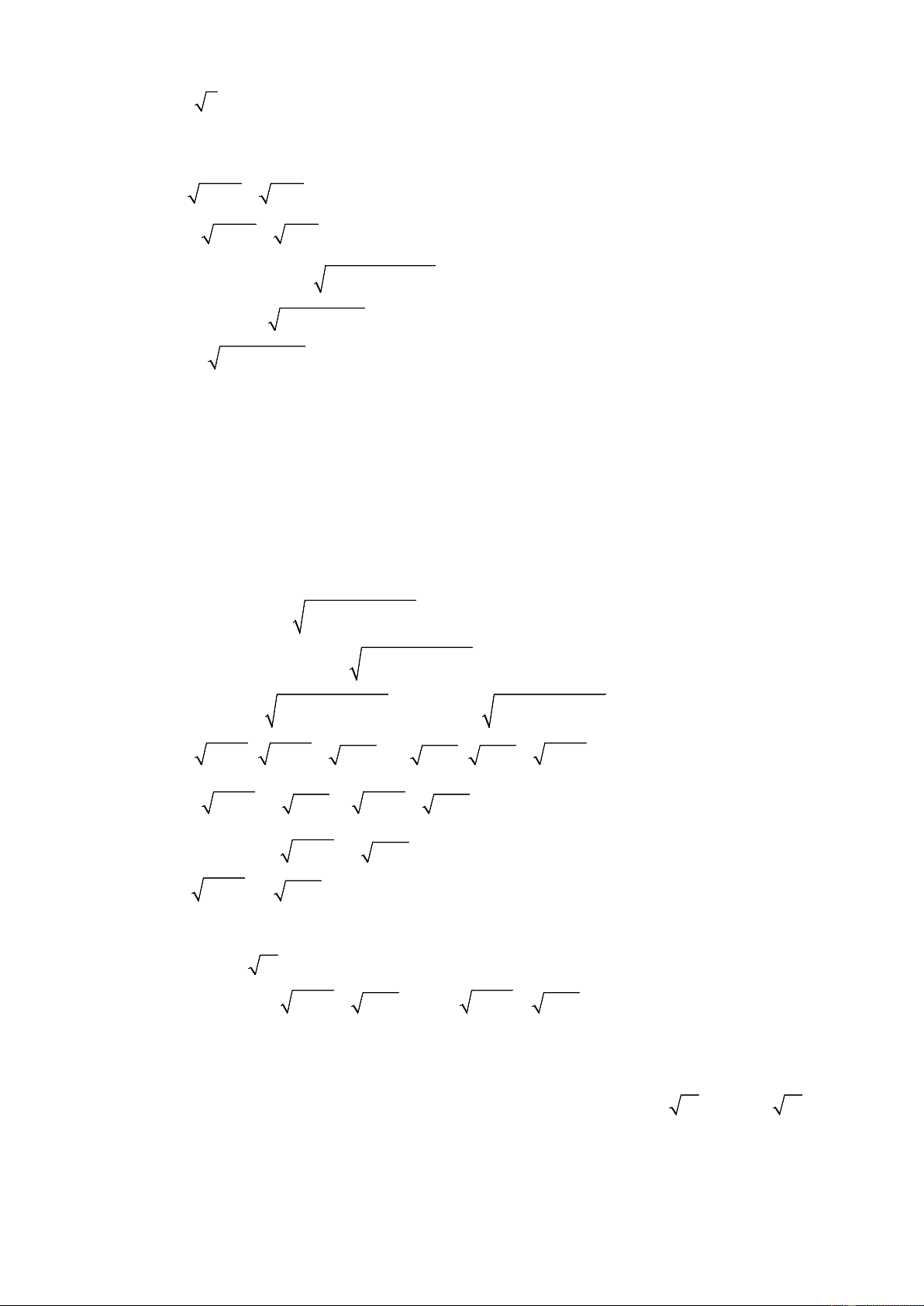
Preview text:

PHÒNG GD&ĐT QUẬN CẦU GIẤY
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
TRƯỜNG THCS CẦU GIẤY NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Bài 1: (2 điểm) Tính giá trị biểu thức 2 − 3 2 + 3
A = (2 6 − 4 3 + 5 2 ).3 6 B = + 2 + 3 2 − 3
C = 48 −10 7 + 4 3 + 2 + 3 Bài 2:
(1,5 điểm) Giải các phương trình sau
a) x − 3 x − 4 = 0 b) 2x −1 + x −1 = 5 c) 2 x + x + = ( 2 2 7 3 x + ) 1 .( x + 3) x + 7 1 3 x + 8 Bài 3:
(2,5 điểm) Cho biểu thức: A = và B = + +
với x ≥ 0 , x ≠ 1 x −1 x + 2 1− x x + x − 2
a) Tính giá trị của A biết x = 9 + 4 2 b) Rút gọn B
c) Tìm các giá trị nguyên của x để biểu thức P = .
A B có giá trị nguyên Bài 4: (3,5 điểm)
1. Một cột đèn có bóng trên mặt đất dài 8,5 m . Các tia nắng mặt trời tạo với mặt đất một góc
xấp xỉ 38° . Tính chiều cao của cột đèn ? (Kết quả làm tròn đến 1 chữ số thập phân) 2. Cho A ∆ BC nhọn có 
ABC = 60° , đường cao AH . Đường thẳng qua C vuông góc với AC
cắt đường thẳng AH tại D . Gọi E và F lần lượt là hình chiếu của H trên AC và CD .
a) Nếu AH = 3cm , AC = 5 cm . Tính độ dài các đoạn thẳng HC , HD , CD ?
b) Chứng minh rằng CF.CD = CE.CA .
c) Biết AB + BC = 8 cm , tìm giá trị lớn nhất của diện tích tam giác ABC . Bài 5:
(0,5 điểm) Cho a,b,c là các số thực dương thỏa mãn: ab + bc + ca = abc . Tìm giá trị lớn nhất a b c
của biểu thức: P = + + . bc (a + ) 1 ca (b + ) 1 ab (c + ) 1  HẾT
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1:
A = (2 6 − 4 3 + 5 2 ).3 6
A = 2 6.3 6 − 4 3.3 6 + 5 2.3 6 A = 36 −12 18 +15 12 2 2
A = 36 −12 3 .2 +15 2 .3
A = 36 −12.3 2 +15.2 3 = 36 − 36 2 + 30 3 2 − 3 2 + 3 B = + 2 + 3 2 − 3 ( − )2 ( + )2 2 3 2 3 B = ( + 2 + 3 ).(2 − 3) (2− 3).(2+ 3) B = ( − )2 + ( + )2 2 3 2 3 B = 2 − 3 + 2 + 3
B = 2 − 3 + 2 + 3 = 4
C = 48 −10 7 + 4 3 + 2 + 3 C = − ( + )2 48 10 2 3 + 2 + 3 C = 48 −10. 2 + 3 + 2 + 3 C = 48 − 20 −10 3 + 2 + 3 C = 28 −10 3 + 2 + 3 C = ( − )2 5 3 + 2 + 3
C = 5 − 3 + 2 + 3 = 5 − 3 + 2 + 3 = 7 Bài 2:
a) x − 3 x − 4 = 0 (điều kiện: x ≥ 0 )
⇔ x + x − 4 x − 4 = 0
⇔ (x + x )−(4 x + 4) = 0 ⇔ x.( x + ) 1 − 4 ( x + ) 1 = 0
⇔ ( x − 4).( x + ) 1 = 0
⇔ x − 4 = 0 (do x +1 > 0 với mọi x ≥ 0 ) ⇔ x = 4
⇔ x = 16 (thỏa mãn điều kiện)
Vậy phương trình có nghiệm x = 16 b) 2x −1 + x −1 = 5
(điều kiện: x ≥1)
⇔ ( x − + x − )2 2 2 1 1 = 5
⇔ 2x −1+ x −1+ 2. (2x − ) 1 .( x − ) 1 = 25 ⇔ 2
3x − 2 + 2. 2x − 3x +1 = 25 ⇔ 2
2. 2x − 3x +1 = 27 − 3x
(điều kiện: x ≤ 9) ⇔ 2 2
8x −12x + 4 = 9x −162x + 729 ⇔ 2
x −150x + 725 = 0 ⇔ 2
x − 5x −145x + 725 = 0
⇔ (x − 5).(x −145) = 0 ⇔ x − 5 = 0
(do đk x ≤ 9 nên x −145 < 0 )
⇔ x = 5 (thỏa mãn điều kiện 1≤ x ≤ 9 )
Vậy phương trình có nghiệm x = 5 c) 2 x + x + = ( 2 2 7 3 x + )
1 .( x + 3) (điều kiện: x ≥ 3 − ) ⇔ ( 2 x + ) 1 + ( x + ) − ( 2 2 3 3 x + ) 1 .( x + 3) = 0 ⇔ ( 2 x + ) 1 − ( 2
x + ) ( x + ) + ( x + ) − ( 2 1 . 3 2 3 x + ) 1 .( x + 3) = 0 ⇔ 2 x +1 ( 2 x +1 − x + 3 ) + x + ( 2 2 3 x + 3 − x +1) = 0
⇔ ( 2x +1− x + ).( 2 2 3 x +1 − x + 3 ) = 0 Trường hợp 1: 2
x +1 − 2 x + 3 = 0 2
⇔ x +1 = 2 x + 3 2
⇔ x +1 = 4x +12 2
⇔ x − 4x −11 = 0 Ta có 2
⇔ x − 4x −11 = 0 2
⇔ x − 4x = 11 ⇔ x − x + = ⇔ (x − )2 2 4 4 15 2 = 15
⇔ x = 2 ± 15 (thỏa mãn điều kiện) Trường hợp 2: 2
x +1 − x + 3 = 0 ⇔ 2 x +1 = x + 3 ⇔ 2 x +1 = x + 3 ⇔ 2
x − x − 2 = 0
⇔ (x − 2).(x + ) 1 = 0 ⇔ x = 1 − hoặc x = 2 (thỏa mãn điều kiện)
Kết hợp với điều kiện ta được phương trình có tập nghiệm S = {2 − 15; 1 − ;2;2 + 15} . Bài 3: a) Ta có: x = + = + + = ( + )2 9 4 2 8 2.2 2.1 1
2 2 1 (thoả mãn điều kiện) ⇒ x = ( + )2 2 2 1
= 2 2 +1, thay vào biểu thức A , ta có: 2 2.(2 2 + + + + )1 2 2 1 7 2 2 8 A = = = = 2 2 +1 2 2 +1−1 2 2 2 2
Vậy x = 9 + 4 2 , thì A = 2 2 +1
b) Với x ≥ 0 , x ≠ 1 ta có: 1 3 x + 8 B = + + x + 2 1− x x + x − 2 1 3 x + 8 = − + x + 2 x −1
( x +2)( x − )1 3 + x −1 ( x 2) x + 8 = ( − + x + 2)( x − ) 1
( x +2)( x − )1 ( x +2)( x − )1
x −1− 3( x + 2) + x + 8 =
( x +2)( x − )1
x −1− 3 x − 6 + x + 8 − + = x 2 x 1 ( = x + 2)( x − ) 1
( x +2)( x − )1 ( x − )2 1 − = x 1 ( = x + 2)( x − ) 1 x + 2 x + 7 x −1 x + 7 5 c) Ta có: P = . A B = . = =1+ x −1 x + 2 x + 2 x + 2 5
Ta có: x ∈, để P ∈ ⇒
∈ ⇒ 5 x + 2 ⇒ x + 2∈Ö (5) ⇒ x + 2∈{ 1 ± ;± } 5 x + 2
Mà x + 2 ≥ 2 với x ≥ 0 , x ≠ 1
Do đó: x + 2 = 5 ⇒ x = 3 ⇒ x = 9 (thoả mãn)
Vậy x = 9 thì P = .
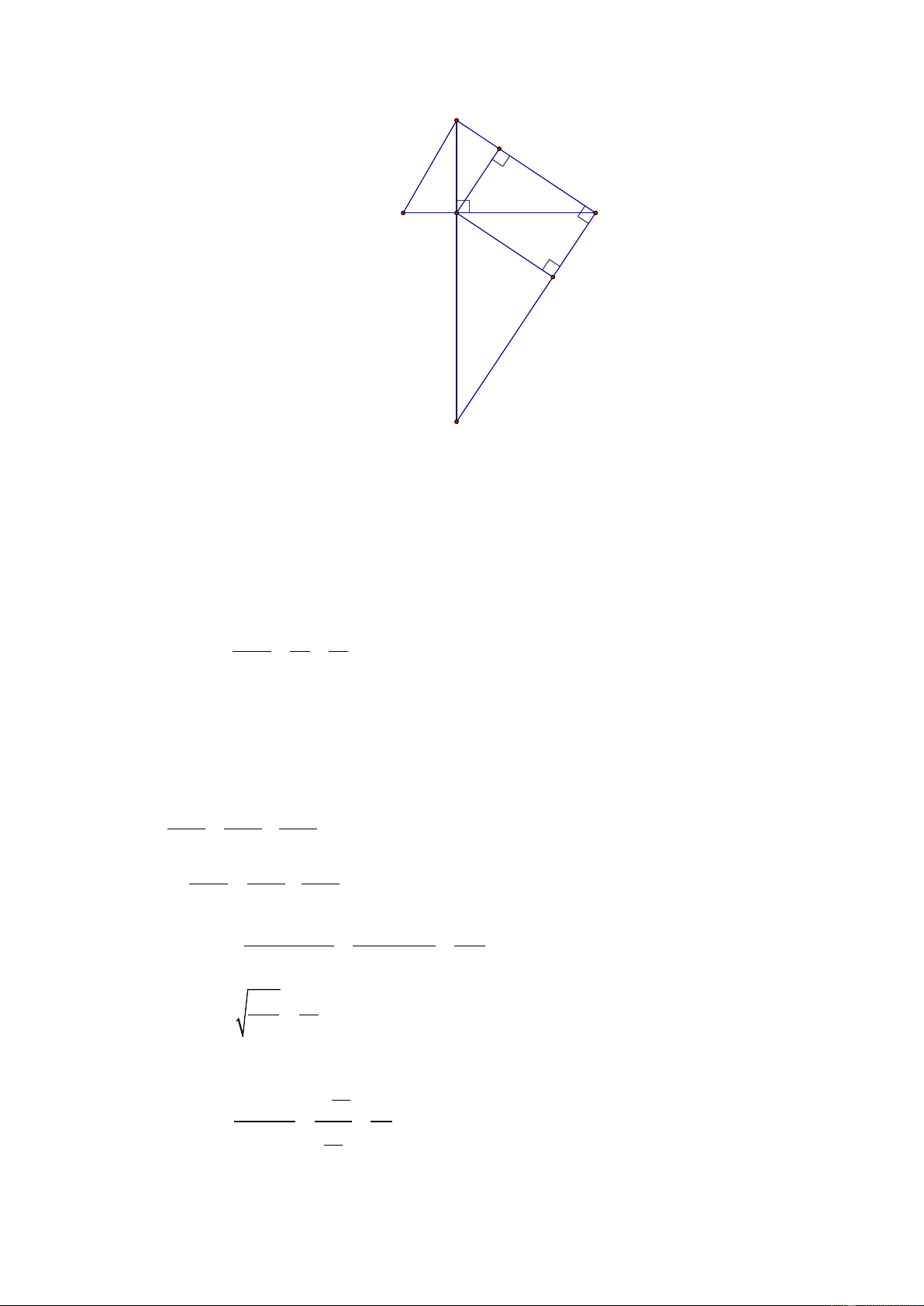
A B có giá trị nguyên. Bài 4: A E 60° B H C F D
a) Nếu AH = 3cm , AC = 5 cm . Tính độ dài các đoạn thẳng HC , HD , CD ? +) Xét A
∆ HC vuông tại H , đường cao HE ta có: 2 2 2
AH + HC = AC (định lý Py-ta-go) 2 2 2 2 2
⇒ HC = AC − AH = 5 − 3 = 25 − 9 =16 ⇒ HC = 4 (cm) 2
HC = CE.AC (quan hệ giữa cạnh và đường cao tam giác vuông) 2 2 HC 4 16 ⇒ CE = = = = 3, 2 (cm) AC 5 5
+) Xét tứ giác HECF có:   
HEC = ECF = HFC = 90°
⇒ tứ giác HECF là hình chữ nhật (dấu hiệu nhận biết)
⇒ HF = CE = 3, 2 (cm) +) Xét C
∆ HD vuông tại H , đường cao HF ta có: 1 1 1 = +
(quan hệ giữa cạnh và đường cao tam giác vuông) 2 2 2 HF HC HD 1 1 1 ⇒ = − 2 2 2 HD HF HC 2 2 HC .HF 4 . 3, 2 256 2 ( )2 2 ⇒ HD = = = 2 2 2 HC − HF 4 − (3, 2)2 9 256 16 ⇒ HD = = ≈ 5,3 (cm) 9 3
Có: HF.CD = HC.HD (quan hệ giữa cạnh và đường cao tam giác vuông) 16 4. HC.HD 20 3 ⇒ CD = = = ≈ 6,7 (cm) HF 16 3 5
b) Chứng minh rằng CF.CD = CE.CA . +) Xét A
∆ HC vuông tại H , đường cao HE ta có: 2
HC = CE.AC (quan hệ giữa cạnh và đường cao tam giác vuông) ( ) 1 +) Xét C
∆ HD vuông tại H , đường cao HF ta có: 2
HC = CF.CD (quan hệ giữa cạnh và đường cao tam giác vuông) (2) Từ ( )
1 và (2) ⇒ CF.CD = CE.CA (điều phải chứng minh)
c) Biết AB + BC = 8 cm , tìm giá trị lớn nhất của diện tích tam giác ABC . 1 Ta có: S = AH.BC ABC 2 Vì A
∆ BH vuông tại H nên ta có AH = A . B sin B Do đó: 1 1 1 3 3 S = A . B BC.sin B = A . B BC.sin 60° = . .A . B BC = A . B BC ABC 2 2 2 2 4 2 2  AB + BC   8  Mặt khác A . B BC ≤ = = 16      2   2 
Dấu “=” xảy ra khi AB = BC = 4 cm Do đó: 3 S ≤ .16 = 4 3 ∆ ( 2 cm ABC ) 4 Vậy 2 max S = 4 3 cm khi A
∆ BC cân tại B . ABC ∆ Bài 5: Ta có: a a a a 1  a a  = = = ≤  +  bc (a ) 1 abc bc ab bc ca bc
b (a c) c (a b) 4  b (a c) c (a b)  + + + + + + + + + +  
Tương tự ta chứng minh được: b 1  b b  ≤  +  ac (b a) 4  a (b c) c (a b)  + + +   c 1  c c  ≤  +  ab (c ) 1 4  b (a c) a (b c)  + + +    + + +  Do đó a b c 1 a c b c a b P = + + ≤  + +  bc (a ) 1 ca (b ) 1 ab (c ) 1 4  b (a c) a (b c) c (a b)  + + + + + +   1  1 1 1 
1 ab + bc + ca 1 ⇔ P ≤ + + = . =   4  a b c  4 abc 4 1 ⇒ max P = 4
Dấu bằng xảy ra khi b (a + c) = c (a + b) = a (b + c) ⇔ ab + bc = ac + bc = ab + ac
⇔ abc − ac = abc − ab = abc − bc .
⇔ ab = bc = ca mà ab + bc + ca = abc ⇔ a = b = c = 3  HẾT