Đề thi giữa kì 1 Toán 9 năm 2020 – 2021 trường THCS Giảng Võ – Hà Nội
Đề thi giữa kì 1 Toán 9 năm 2020 – 2021 trường THCS Giảng Võ – Hà Nội được biên soạn theo hình thức đề thi tự luận, đề gồm 05 câu, thời gian làm bài 90 phút, đề thi có đáp án và lời giải chi tiết. Mời bạn đọc đón xem.
Preview text:
TRƯỜNG THCS GIẢNG VÕ
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 ---------- NĂM HỌC 2020 - 2021 THCS.TOANMATH.com MÔN TOÁN - LỚP 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề) Bài 6:
(2 điểm) Thực hiện phép tính a) A = + ( − )2 3 125 2 5 + b) B = ( + ) 20 5 2 7 11− 4 7 − 5 + 2 0 cot 32 c) 2 0 2 0 0 0
C = sin 25 + sin 65 − tan 35 + cot 55 − 0 tan 58 Bài 7: (1,5 điểm).
Giải các phương trình sau:
a) 9x − 27 − x − 3 = 6 . b) 2
x + 2x +1 − x +1 = 0 Bài 8: (2,5 điểm) x − 2 2 x 5 x − 2 x +1
Cho hai biểu thức A = và B = − −
với x > 0; x ≠ 4 x + x +1 x − 2 x − 2 x x
1) Tính giá trị biểu thức A khi x = 9 .
2) Rút gọn biểu thức B .
3) Tìm các giá trị của x để 1 B ≤ − . 2 6 A
4) Tìm giá trị lớn nhất của biểu thức M = B Bài 9: (3,5 điểm)
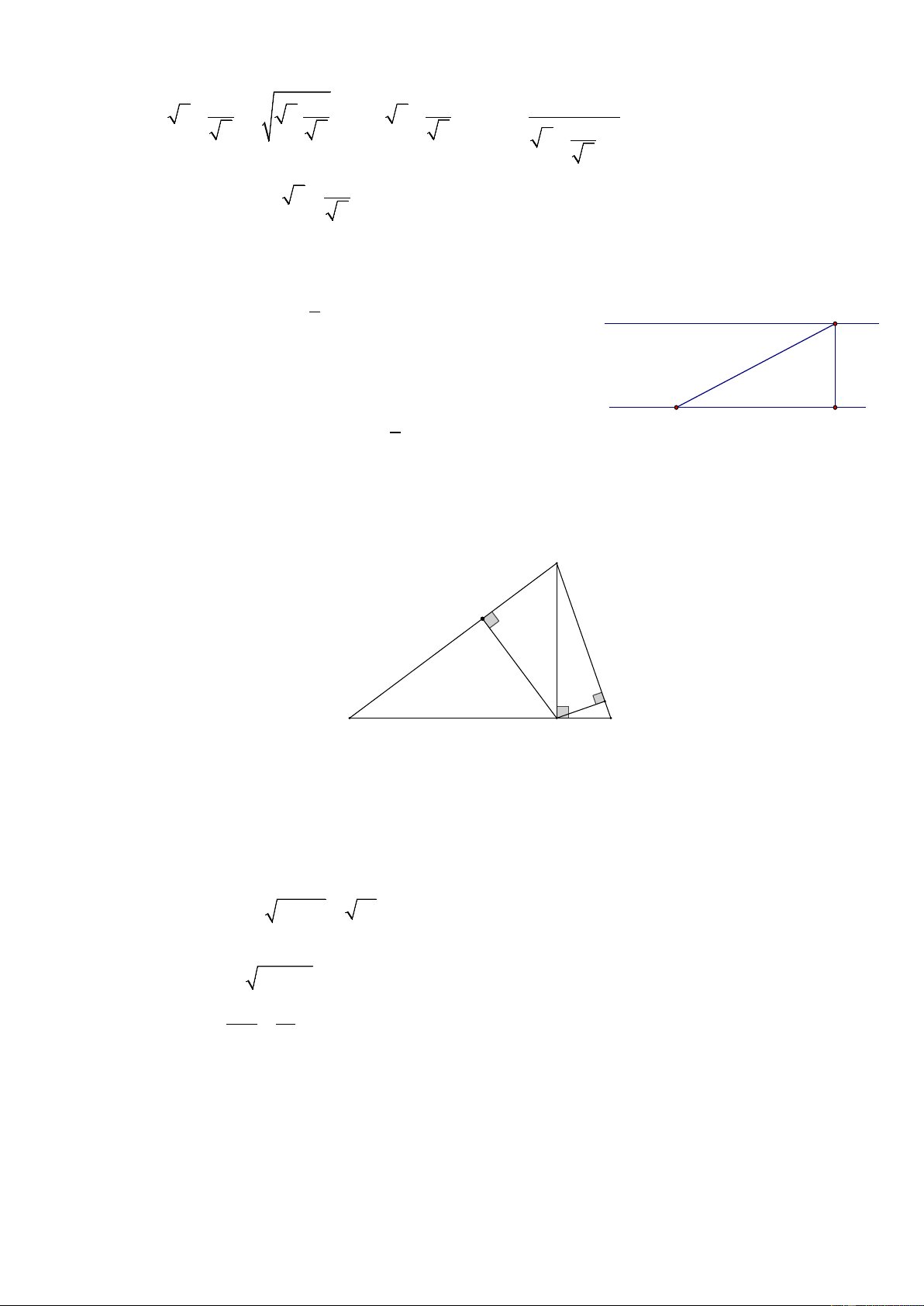
1) Một con thuyền đi qua một khúc sông theo hướng từ C
B đến C (như hình vẽ) với vận tốc 3,5km / h trong 12
phút. Biết rằng đường đi của thuyền tạo với bờ sông
một góc 25° . Hãy tính chiều rộng của khúc sông ? (Kết 25°
quả tính theo đơn vị km ,làm tròn kết quả đến chữ số B H thập phân thứ hai).
2) Cho tam giác ABC nhọn có đường cao AH . Gọi E
là hình chiếu của H trên AB .
a. Biết AE = 3, 6cm ; BE = 6, 4cm . Tính AH , EH và góc .
B (Số đo góc làm tròn đến độ)
b. Kẻ HF vuông góc với AC tại F. Chứng minh A .
B AE = AC.AF.
c. Đường thẳng qua A và vuông góc với EF cắt BC tại D ; EF cắt AH tại . O S Chứng minh rằng AOE S = ADC 2 2 sin . B sin C
Bài 10: (0,5 điểm) Giải phương trình 3
2 2x −1 = 8 − x + 3 . HẾT
TRƯỜNG THCS GIẢNG VÕ
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 ---------- NĂM HỌC 2020 - 2021 THCS.TOANMATH.com MÔN TOÁN - LỚP 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề) 2 Câu 1.
A = 3 125 + (2 − 5) =15 5 + 2 − 5 =15 5 + 5 − 2 = 2(8 5 − ) 1 a) + B = ( + ) 20 5 2 7 11− 4 7 − 5 + 2 2 ( + = 2 + 7 ) (2− 7)2 2 5 ( 5) − ( 5+2) ( + = 2 + 7 ) 5 (2 5 ) 2 − 7 − ( 5+2) = (2+ 7)( 7 − 2)− 5 = 7 − 4 − 5 = 3 − 5 0 cot 32 b) 2 0 2 0 0 0
C = sin 25 + sin 65 − tan 35 + cot 55 − 0 tan 58 0 cot 32 2 0 2 0 0 0
C = sin 25 + cos 25 − tan 35 + tan 35 − = 1+ 0 −1 = 0 . 0 cot 32 Câu 2.
a) 9x − 27 − x − 3 = 6 (ĐKXĐ: x ≥ 3 )
⇔ 3 x − 3 − x − 3 = 6 ⇔ 2 x − 3 = 6 ⇔ x − 3 = 3 ⇔ x − 3 = 9
⇔ x =12 (thỏa mãn ĐKXĐ) Kết luận: x ∈{ } 12 b) 2
x + 2x +1 − x +1 = 0 (ĐKXĐ: x ≥ 1 − ) ⇔ (x + )2 1 − x +1 = 0
⇔ x +1( x +1− ) 1 = 0 x +1 = 0 x +1 = 0 x = 1 − (TM ) ⇔ ⇔ ⇔ + − = x +1 = 1 x = 0 (TM ) x 1 1 0 Kết luận: x ∈{ 1 − ; } 0 Câu 3. 1) Khi x = 9 ⇒
x = 3 thỏa mãn điều kiện.Thay vào biểu thức A ta được: 3 − 2 1 1 A = =
.Vậy khi x = 9 thì A = 9 + 3 +1 13 13 2 x 5 x − 2 x +1
2) Với x > 0; x ≠ 4 ta có: B = − − x − 2 x − 2 x x 2 x 5 x − 2 x +1 = − − x − 2 x ( x − 2) x + − x x x − ( x )1( x 2 2 . 5 2 ) = − − x ( x − 2) x ( x − 2) x ( x − 2)
2x − (5 x − 2) − ( x + ) 1 ( x − 2) = x ( x − 2)
2x − 5 x + 2 − x + x + 2 = x ( x − 2) − + ( x − x x )2 2 4 4 x − 2 = = = x ( x − 2) x ( x − 2) x x − 2 Vậy B =
với x > 0; x ≠ 4 x x − x − x − + x
3) Với x > 0; x ≠ 4 để 1 2 1 2 1 2 4 B ≤ − ⇔ ≤ − ⇔ + ≤ 0 ⇔ ≤ 0 2 x 2 x 2 2 x 3 x − 4 ⇔ ≤ 4 16
0 mà 2 x > 0 nên 3 x − 4 ≤ 0 ⇔ 3 x ≤ 4 ⇔ x ≤ ⇔ x ≤ 2 x 3 9 16 1
Kết hợp với điều kiện ta được 0 < x ≤ thì B ≤ − 9 2 6 − − A ( x 2) 6 x − ( x 2 6 2 ) x 6 x d) Ta có: M = = : = . = B x + x +1 x x + x +1 x − 2 x + x +1 6 ⇒ 1 M = do x > 0 ⇒ x > 0;
> 0 . Áp dụng bất đẳng thức Cô si với 2 số 1 x + +1 x x dương ta được: 1 1 1 6 x + ≥ 2 x. = 2 ⇒ x + +1 ≥ 3 ⇔ ≤ 2 hay M ≤ 2 1 x x x x + +1 x 1 Dấu "=: xảy ra x =
⇒ x = 1( thỏa mãn đk) x
Vậy Max M = 2 ⇔ x = 1 Câu 4. (3,5 điểm) 1 C 1) Đổi: 12 phút = giờ 5
Gọi chiều rộng của khúc sông là CH . Đường đi của ⊥ con thuyền là BK suy ra 0 CH BK , CBH = 25 25° 1 B H
Quãng đường BC dài là: 3,5. = 0,7 (km) 5 Xét B
∆ HC vuông tại H có: 0 0
CH = sin 25 . BC = sin 25 .0, 7 ≈ 0, 29 (km)
Vậy chiều rộng khúc sông khoảng 0,29 (km). A 3,6 E 6,4 F B C H 2)
a. Biết AE = 3, 6cm ; BE = 6, 4cm . Tính AH , EH và góc .
B (Số đo làm tròn đến độ)
Ta có: AB = AE + EB = 3, 6 + 6, 4 = 10cm
Áp dụng hệ thức lượng trong tam giác vuông AHB có AHB = 90 ; ° HE ⊥ AB Ta có: 2
AH = AE.AB
⇒ AH = 3, 6.10 = 36 = 6cm Và: 2
EH = AE.EB
⇒ EH = 3, 6.6, 4 = 4,8cm AH 6 Sin B = = = 0,6 AB 10 ⇒ B ≈ 36 52 ° ' b. Chứng minh A .
B AE = AC.AF Xét A ∆ BH có : AHB = 90 ; ° HE ⊥ AB
Áp dụng hệ thức lượng trong tam giác vuông ta có: 2 A . B AE = AH (1)
Áp dụng hệ thức lượng trong tam giác vuông AHC có: AHC = 90 ; ° HF ⊥ AC 2
⇒ AF.AC = AH (2)
Từ (1) và (2) ⇒ A .
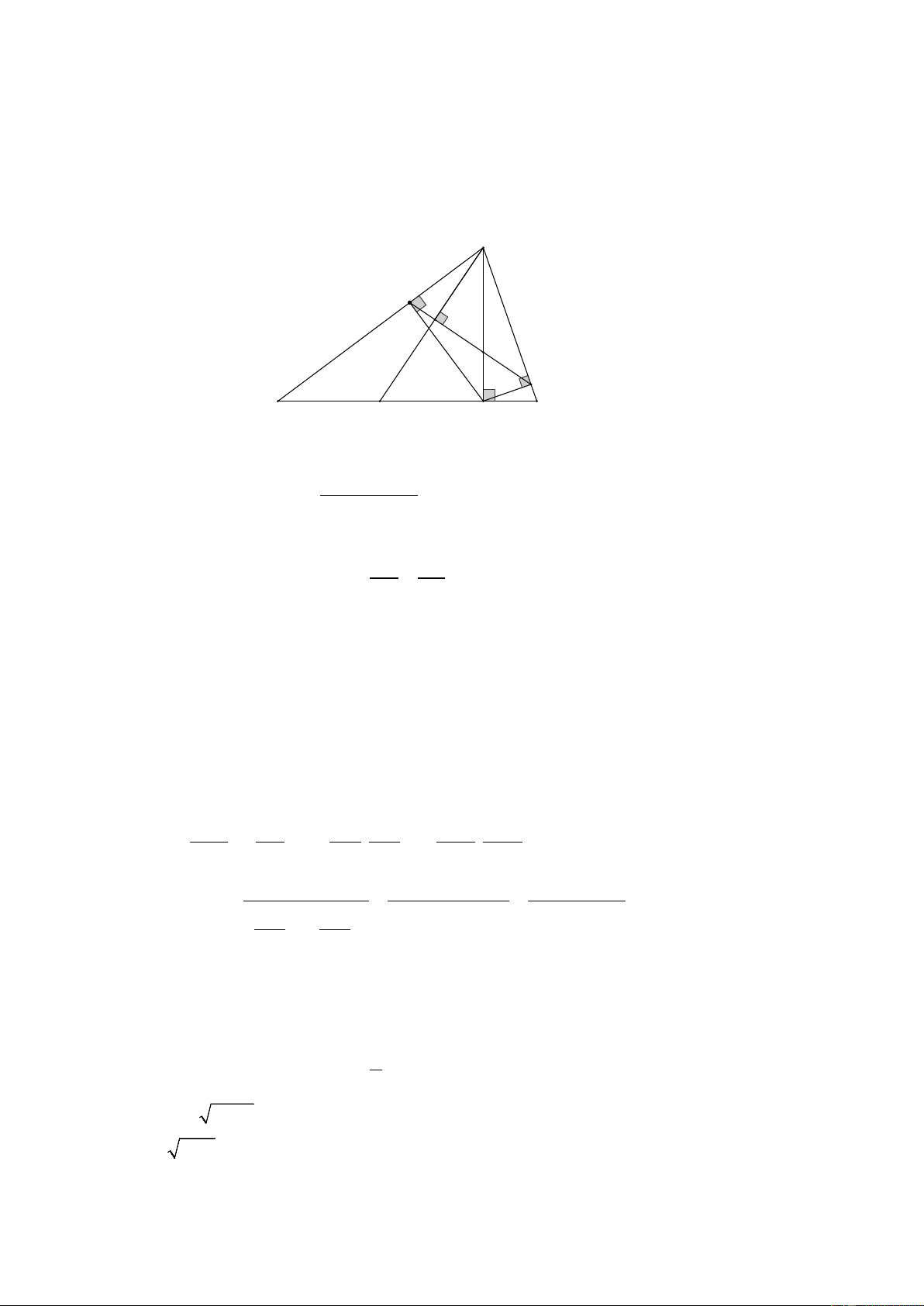
B AE = AC.AF (dpcm). c) A 3,6 E I 6,4 O F B C D H S Chứng minh: AOE S = ADC 2 2 sin . B sin C
Gọi I là giao điểm của AD và EF AE AF
Ta có: AE.AB = AF.AC ⇒ = AC AB
Dễ dàng chứng minh được ∆ E A F ∽ A ∆ CB ( . c g.c) ⇒ = = AFI ABH ;ACD AEO (1) Mà + 0 CAD AFI = 90 + 0 EAO ABH = 90 ⇒ = EAO CAD (2) Từ (1);(2) ⇒ A
∆ DC ∽ A
∆ OE (g.g) 2 2 2 2 S AC AC AH AC AH ADC ⇒ = = . = . 2 2 S AE AH AE AH AE AOE S S S AOE AOE AOE ⇒ S = = = ADC 2 2 2 2 2 2
AH AE sin C. os c EAO sin C.sin B .
AC AH (đpcm) Câu 5. Điề 1
u kiện 2x −1 ≥ 0 ⇔ x ≥ . 2 Đặt 2
2x −1 = u ⇒ u = 2x −1. 3 3 3
x + 3 = v ⇒ v = x + 3 ⇔ 2v = 2x + 6 . 3 2
⇒ 2v − u = 2x + 6 − (2x − ) 1 = 7 3 2
⇔ 2v − u − 7 = 0 8 − v Mà 3
2 2x −1 = 8 − x + 3 ⇔ 2u = 8 − v ⇔ u = . 2 2 8 − v 3 ⇒ 2v − − 7 = 0 2 2 64 −16v + v 3 ⇔ 2v − − 7 = 0 4 3 2
⇔ 8v − 64 +16v − v − 28 = 0 3 2
⇔ 8v − v +16v − 92 = 0 ⇔ (v − )( 2
2 8v +15v + 46) = 0 ⇔ v = 2 ⇔ x + 3 = 8
⇔ x = 5 (thỏa mãn điều kiện). Vậy x = 5 . HẾT