Đề thi giữa kì 1 Toán 9 năm 2020 – 2021 trường THCS Phú Diễn – Hà Nội
Nhằm kiểm tra đánh giá chất lượng dạy và học môn Toán lớp 9 định kỳ, ngày … tháng 11 năm 2020, trường THCS Phú Diễn, Bắc Từ Liêm, thành phố Hà Nội tổ chức kỳ thi kiểm tra chất lượng giữa học kỳ 1 môn Toán 9 năm học 2020 – 2021. Mời bạn đọc đón xem.
Preview text:
TRƯỜNG THCS PHÚ DIỄN
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 ---------- NĂM HỌC 2020 - 2021 THCS.TOANMATH.com MÔN TOÁN - LỚP 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Câu 1. Tính giá trị biểu thức . 1 1)5 20 − 3 12 + 5 − 2 27 + + − 5 2) 125 2 6 2 5 9 5 2 − 5 3) + 10 − 1 5 cot16° 2 2
4) sin 32° + 3cos 23° − cos 58° + 3cos 67° − tan74° Bài 6: Giải các phương trình.
a) 4x + 20 − 2 x + 5 + 9x + 45 = 6 . b) 2
9x − 6x +1 = 9 .
c) 2x −1 − 2 x +1 = 0 . x + 3 4 − 1 Bài 7:
Cho hai biểu thức A = B = +
(với x ≥ 0 ; x ≠ 4 ). x − và 4 x − 4 x − 2
a) Tính giá trị của A khi x = 9 .
b) Rút gọn biểu thức B . A c) So sánh P =
với 1 khi x > 4 . B Câu 4.
1) Tính chiều cao cột cờ, biết bóng của cột cờ được chiếu bởi ánh sáng của Mặt Trời
xuống đất dài 10,5m và góc tạo bởi tia sáng với mặt đất là 35 45 ° ′
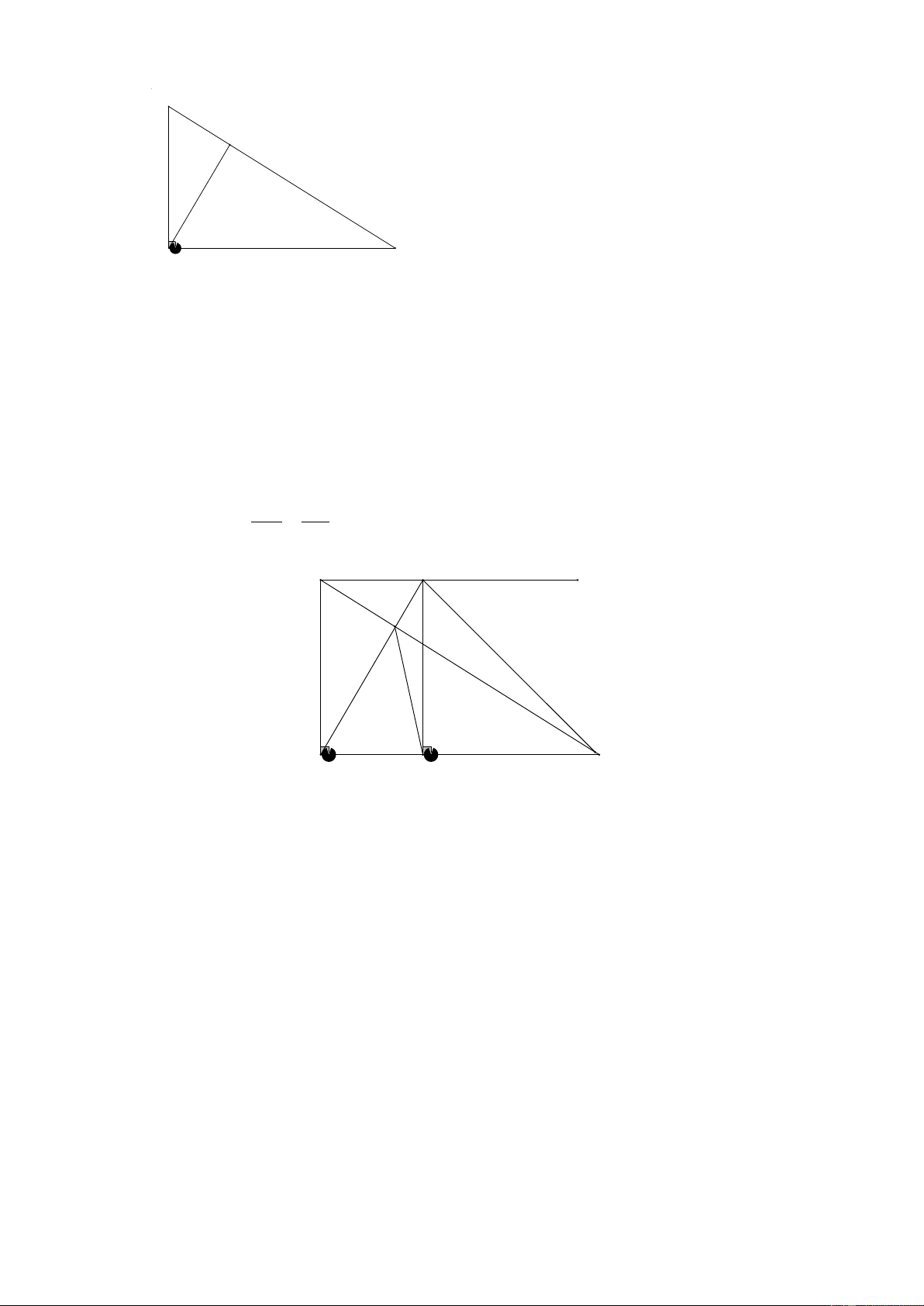
2) Cho tam giác ABC vuông tại ,
A AH là đường cao .
a) Biết BH = 3,6c ,
m CH = 6, 4cm Tính AH , AC, AB và HAC
b) Qua B kẻ tia Bx / / AC , Tia Bx cắt AH tại K , Chứng minh: AH.AK = BH.BC 3
c) Kẻ KE ⊥ AC tại E . Chứng minh: HE =
KC với số đo đã cho ở câu a 5
d) Gọi I giao điểm câc đường phân giác các góc trong của tam giác ABC . Gọi r là r 1
khoảng cách từ I đến cạnh BC . Chứng minh: ≥ AH 3
Câu 5. Cho x, y là hai số thực dương thỏa mãn x + y ≥ 3 . 28 1
Tìm giá trị nhỏ nhất của biểu thức 2 2
P = 2x + y + + x y
__________ THCS.TOANMATH.com __________
TRƯỜNG THCS PHÚ DIỄN
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 ---------- NĂM HỌC 2020 - 2021 THCS.TOANMATH.com MÔN TOÁN - LỚP 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1. 1 1) 5 20 − 3 12 + 5 − 2 27 5 25 = 10 5 − 6 3 +
− 6 3 = 10 5 + 5 −12 3 = 11 5 −12 3 5 2) 125 + 2 + 6 − 2 5 = + + ( − )2 5 5 2 5 1 = 5 5 + 2 + 5 −1 = 6 5 +1 9 5 2 − 5 3) + 10 −1 5 9 ( 10 + ) 1 5 ( 10 − ) 1 = + 10 −1 5 = 10 +1+ 10 −1 = 2 10 cot16° 4) 2 2
sin 32° + 3cos 23° − cos 58° + 3cos 67° − tan74° tan 74° 2 2
= cos58° + 3cos 23° − cos58° + 3sin 23° − tan74° = ( 2 2
3 cos 23° + sin 23°) −1 = 3 −1 = 2 Câu 2.
a) 4x + 20 − 2 x + 5 + 9x + 45 = 6 ĐK: x ≥ 5 −
⇔ 2 x + 5 − 2 x + 5 + 3 x + 5 = 6 ⇔ 3 x + 5 = 6 ⇔ x + 5 = 2 ⇔ x + 5 = 4 ⇔ x = 1 − (Thỏa mãn) Vậy x = 1 − . b) 2 9x − 6x +1 = 9 ⇔ ( x − )2 3 1 = 9 ⇔ 3x −1 = 9 TH1: 3x −1 = 9 TH2: 3x −1 = 9 − ⇔ 3x =10 ⇔ 3x = 8 − 10 ⇔ = − ⇔ 3x 8 x = (Thỏa mãn) 3 8 − ⇔ x = (Thỏa mãn) 3 10 8 Vậy x ∈ ; − . 3 3
c) 2x −1 − 2 x +1 = 0 ĐK: 1 x ≥ 2
⇔ 2x −1 = 2 x −1 2 x −1≥ 0 ⇔ 2x−1= (2 x − )2 1 1 x ≥ ⇔ 4
2x−1= 4x−4 x +1 1 x ≥ ⇔ 4
2x−4 x + 2 = 0 1 x ≥ ⇔ 4
x−2 x +1= 0 1 x ≥ 4 ⇔ ( x− )2 1 = 0 1 x ≥ ⇔ 4 x =1 (TM ) Vậy x = 1 . Câu 3.
a) Với x = 9 (thỏa mãn) ⇒ x = 3.
Thay x = 9 và x = 3 vào A ta được x + 3 3 + 3 6 A = = = x − 4 9 − 4 5 6
Vậy với x = 9 thì A = . 5 4 − 1 b) B = + x − 4 x − 2 4 − 1 = ( + x − 2)( x + 2) x − 2 4 − x + 2 = ( +
x − 2)( x + 2) ( x − 2)( x + 2) x − 2
= ( x −2)( x +2) 1 = . x + 2 A x + 3 1 x + 3 x + 3 c) Ta có: P = = : = x + = B x − 4 x + 2
( x +2)( x −2).( 2) x − 2 x + 3 x + 3 x − 2 5 Xét hiệu P −1 = −1 = − = x − 2 x − 2 x − 2 x − 2 Ta có: x > 4 ⇔ x > 2 ⇔ x − 2 > 0 5 ⇒ > 0 x − 2 ⇒ P −1 > 0 ⇒ P > 1 Vậy P > 1 Câu 4. 1) B 35°45' A C 10,5m
Gọi AB là chiều cao cột cờ. AC là bóng của cột cờ trên mặt đất
Xét tam giác ABC vuông tại A
AB = AC.tan C ⇒ AB = 10,5.tan 35 45 ° ′ ≈ 6,75(m)
Vậy cột cờ cao xấp xỉ 6,75(m) 2) B H A C
Tam giác ABC vuông tại ; A AH ⊥ BC
BC = BH + HC = 3, 6 + 6, 4 = 10(cm) 2
AH = BH .CH = 3,6.6, 4 ⇒ AH = 4,8(cm) 2
AB = BH .BC = 3, 6.10 = 36 ⇒ AB = 6(cm) 2
AC = CH .BC = 6, 4.10 = 64 ⇒ AC = 8(cm)
Tam giác AHC vuông tại H nên: HC 6,4 sin HAC = = ⇒ HAC ≈ 53 8 ° ′ AC 8 K x B H A C E b) Ta có: BK / / AC
⇒ AB ⊥ BK AB ⊥ AC
+)Tam giác ABC vuông tại ; A AH ⊥ BC 2
⇒ AB = BH.BC
+)Tam giác ABK vuông tại B;B H ⊥ AK 2 ⇒ AB = AH.AK
Suy ra AH.AK = BH.BC
c) Xét tam giác AHC và tam giác AEK có = 0 AHC AEK = 90 CAK chung Vậy tam giác A ∆ HC ∼ A
∆ EK (g − g) AH AC ⇒ = AH AE ⇒ = AE AK AC AK
Xét tam giác AHE và tam giác ACK có AH AE = (cmt) AC AK CAK chung Vậy tam giác A ∆ HE A
∆ CK (c − g − c) HE AH 4,8 3 ⇒ = = = CK AC 8 5 3 ⇒ HE = KC 5 B K x H D r r N I r A C M E
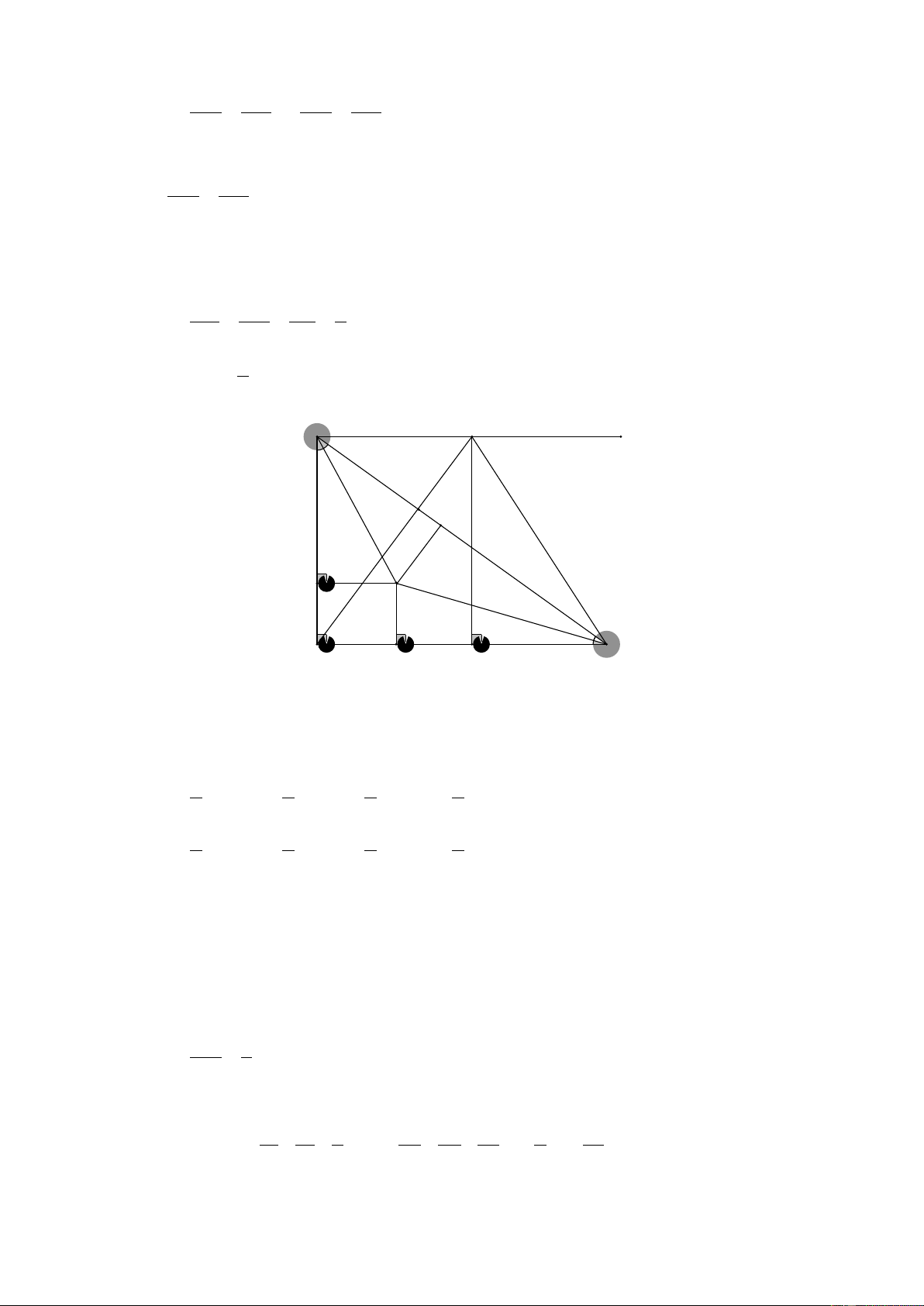
d) Kẻ ID ⊥ BC IM ⊥ AC , IN ⊥ AB ⇒ IM = IN = ID = r S = S + S + S ABC IAB IAC IBC 1 1 1 1
⇒ AH.BC = I . D BC + IM .AC + IN.AB 2 2 2 2 1 1 1 1
⇒ AH.BC = I . D BC + IM .AC + IN.AB 2 2 2 2
⇒ AH.BC = r.BC + r.AC + r.A B
⇒ AH.BC = r(BC + AC + AB)
Mà AB < BC; AC < BC (Vì tam giác ABC vuông tại A )
⇒ AH.BC = r (BC + AC + AB) < r (BC + BC + BC) = 3r.BC
⇒ AH < 3r r 1 ⇒ > AH 3 Câu 5. 2 2 14 14 7 1 1 y 1 y Ta có: 2 2 P = + + x + + + + x + x x 4
2y 2y 2 4 2 2 14 14 7 1 1 y 1 1 3 2 P = + + x + + + + ( 2 x + 4) + ( 2 y + ) 1 − x x 4
2y 2y 2 4 2 2
Áp dụng bất đẳng thức Cô-si ta có: 14 14 7 +) 2 3 +
+ x ≥ 3 49.7 . Dấu " = " xảy ra ⇔ x = 2 x x 4 14 14 7 2 ⇒ + + x ≥ 21 x x 4 2 1 1 y 1 +) 3 + + ≥ 3
. Dấu " = " xảy ra ⇔ y = 1 2 y 2 y 2 8 2 1 1 y 3 ⇒ + + ≥ 2 y 2 y 2 2 +) 2
x + 4 ≥ 4x . Dấu " = " xảy ra ⇔ x = 2 +) 2
y +1 ≥ 2 y . Dấu " = " xảy ra ⇔ y = 1 2 14 14 7 1 1 y 1 1 3 3 3 2 ⇒ P = + + x + + + + ( 2 x + 4) + ( 2 y + ) 1 −
≥ 21+ + x + y − x x 4
2y 2y 2 4 2 2 2 2 3 3 ⇒ P ≥ 21+ + 3 − 2 2
⇒ P ≥ 24 . Dấu " = " xảy ra ⇔ x = 2; y =1 Vậy P
= 24 ⇔ x = 2; y =1 min
__________ THCS.TOANMATH.com __________