Đề thi giữa kì 1 Toán 9 năm 2020 – 2021 trường THCS Sơn Đông – Hà Nội

Nhằm kiểm tra đánh giá chất lượng dạy và học môn Toán lớp 9 định kỳ, ngày … tháng 11 năm 2020, trường THCS Sơn Đông, Sơn Tây, thành phố Hà Nội tổ chức kỳ thi kiểm tra chất lượng giữa học kỳ 1 môn Toán 9 năm học 2020 – 2021. Mời bạn đọc đón xem.

28 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 9

Môn: Toán 9

Thông tin:

6 trang 7 tháng trước

Tác giả:

Profile Hà Việt Anh
PHÒNG GD VÀ ĐT THỊ XÃ SƠN TÂY
T
RƯỜNG THCS SƠN ĐÔNG
----------
THCS.TOANMATH.com
ĐỀ KIỂ
M TRA GIỮA HỌC KÌ I
NĂM HỌC 2019 - 2020
MÔN TOÁN - LỚP 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
ĐỀ 1
Bài 1. ( 2 điểm) Tính
a)
5 12 4 27 6 48+−
b)
( )
300 2 675 5 75 : 3−+
c)
11
5353
−
−+
d)
22
4 23 4 23
+
−+
Bài 2. (2,0 điểm).Giải phương trình :
a)
2 35x +=
; b)
5 9 9 2 4 4 1 36x xx+− ++ +=
.
Bài 3. (2,0 điểm).Cho hai biểu thức
2
1
x
A
x
+
=
−
và
( )
2 3 6 22
0, 1
3 2 56
x x xx
B xx
x x xx
− − −−
= + − ≥≠
+ + ++
.
a) Tính giá trị của biểu thức
tại
25x =
.
b) Chứng minh
3
2
x
B
x
+
=
+
.
c) Tìm tất cả các giá trị nguyên của
x
để
.P AB=
có giá trị nguyên.
Bài 4. (3,5 điểm)
1) Một cột đèn có bóng trên mặt đất dài 6m. Các tia nắng mặt trời tạo với mặt đất một
góc xấp xỉ bằng
0
40
. Tính chiều cao của cột đèn (làm tròn đến mét).
2) Cho tam giác
ABC
vuông tại
A
, đường cao
AH
. Biết
3, 4AB cm AC cm= =
.
a) Tính
AH
b) Gọi
,DE
lần lượt là hình chiếu của
H
trên
AB
và
AC
. Chứng minh tam giác
AED
và tam giác
ABC
đồng dạng.
c) Kẻ trung tuyến
AM
, gọi
N
là giao điểm của
AM
và
DE
. Tính tỉ số diện tích của tam
giác
AND
và tam giác
ABC
Bài 5. (0,5 điểm). Tìm các số
,,xyz
thỏa mãn đẳng thức:
82 14 26 3xyz x y z+ ++= −+ − + −
HẾT
ĐỀ 1
HƯỚNG DẪN GIẢI CHI TIẾT
Bài 1.
a)
5 12 4 27 6 48+−
222
5 2 .3 4 3 .3 6 4 .3=+−
5.2 3 4.3 3 6.4 3=+−
10 3 12 3 24 3=+−
=
23−
b)
( )
300 2 675 5 75 : 3−+
(
)
2 22
10 .3 2 15 .3 5 5 .3 : 3=−+
( )
10 3 2.15 3 5.5 3 : 3=−+
( )
10 30 25 3 : 3= −+
5 3: 3=
5=
c)
11
5353
−
−+
( ) ( )
( )( )
53 53
5353
+−−
=
+−
5353
53
+−+
=
−
23
3
2
= =
d)
22
4 23 4 23
+
−+
( ) ( )
( )( )
24 2 3 24 2 3
4 23 4 23
+ +−
=
−+
( )
2
2
8 43 8 43
4 23
+ +−
=
−
16
16 12
=
−
16
4
=
4=
Bài 2.
PHÒNG GD VÀ ĐT THỊ XÃ SƠN TÂY
TRƯỜNG
THCS SƠN ĐÔNG
----------
THCS.TOANMATH.com
ĐỀ KIỂ
M TRA GIỮA HỌC KÌ I
NĂM HỌC 2019 - 2020
MÔN TOÁN - LỚP 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
a) Điều kiện:
3
2
x
−
≥
2 3 5 2 3 25 11xxx+=⇔ += ⇔ =
(nhận)
Vậy nghiệm của phương trình là:
11x =
b) Điều kiện:
1x ≥−
5 9 9 2 4 4 1 36 15 1 4 1 1 36x x x x xx+ − + + += ⇔ +− ++ +=
12 1 36 1 3 1 9 8x xxx⇔ += ⇔ +=⇔ +=⇔ =
(nhận)
Vậy nghiệm của phương trình
8x =
Bài 3.
a) Tại
25x =
, ta được:
25 2 7
4
25 1
A
+
= =
−
.
2 3 6 22
3 2 56
x x xx
B
x x xx
− − −−
=+−
+ + ++
( )
0, 1xx≥≠
( )( ) ( )( )
( )
( )( )
2
3
4 9 6 22 6 9 3
2
32 32 32
x
x x xx xx x
x
xx xx xx
+
−+−−++ ++ +
= = = =
+
++ ++ ++
.
b)
23 3 4
.. 1
12 1 1
xx x
P AB
xx x x
++ +
= = = = +
−+ − −
Để
.P AB=
có giá trị nguyên thì
4
1x −
nguyên
( ) ( )
( ) { }
4 1 1 4 4, 2, 1,1,2,4x xU⇒ − ⇒ −∈ =−−−
Khi đó:
14 3xx−=−⇒ =−
(loại)
12 1xx−=−⇒ =−
(loại)
11 0xx−=−⇒ =
(thỏa mãn)
11 2 4x xx−=⇒ = ⇒ =
(thỏa mãn)
12 3 9x xx−= ⇒ = ⇒ =
(thỏa mãn)
1 4 5 25x xx−= ⇒ = ⇒ =
(thỏa mãn)
Vậy
{ }
0,4,9,25x∈
.
Bài 4.
1) Gọi
AB
là chiều cao cột đèn.
AC
là độ dài bóng của cột đèn
Góc
là góc tạo bởi tia nắng mặt trời với mặt
đất.
6m
40
°
C
B
A
Xét
ABC∆
vuông tại
:
.tanAB AC C=
( hệ thức cạnh và góc trong tam giác vuông)
0
6.tan 40 5AB = ≈
m
Vậy, chiều cao cột đèn xấp xỉ
5
m.
2)
a) Xét
ABC∆
vuông tại
, đường cao
AH
:
222
1 11
AH AB AC
= +
( hệ thức lượng trong tam giác vuông )
222
1 1 1 25
3 4 144AH
=+=
2
144
25
AH =
12
5
AH =
(cm)
b) Xét
ABH∆
vuông tại
H
, đường cao
HE
:
2
.AH AD AB=
( hệ thức lượng trong tam giác vuông)
Xét
AHC∆
vuông tại
H
, đường cao
HD
2
.AH AE AC=
( hệ thức lượng trong tam giác vuông)
..AD AB AE AC⇒=
AD AE
AC AB
⇒=
Xét
ADE∆
và
ACB∆
:
AD AE
AC AB
=
(chứng minh trên)
BAC
chung
ADE ACB⇒∆ ∆”
(c-g-c)
c) Xét
ABC∆
vuông tại
, đường trung tuyến
AM
AM MB MC⇒==
MA MC=
AMC⇒∆
cân tại
M
MAE MCA⇒=
O
N
M
E
D
H
C
B
A
MA MB=
AMB⇒∆
cân tại
M
NAD ABC⇒=
Có :
OAE OEA=
Mà
OAE ABH=
( cùng phụ
OAD
)
ABH OEA⇒=
Có :
90ABH ACB+=°
90NAE NEA⇒+=°
90ANE⇒=°
Xét
AND∆
và
BAC∆
:
90AND BAC= = °
NAD ABC=
AND BAC⇒∆ ∆”
(g-g)
2
AND
BAC
S
AD
S BC

⇒=


Có
AHB∆
vuông tại
H
, đường cao
HD
:
2
.AH AD AB=
22
2,4
1, 92
3
AH
AD
AB
⇒= = =
(cm)
22
1, 92
0,4096
3
AND
BAC
S
AD
S BC

⇒= = =


Bài 5. (0,5 điểm). Tìm các số
,,xyz
thỏa mãn đẳng thức:
82 14 26 3xyz x y z+ ++= −+ − + −
Lời giải
Điều kiện :
1x ≥
;
2y ≥
;
3z ≥
82 14 26 3xyz x y z+ ++= −+ − + −
12 11 24 2 4 36 39 0xxy y zz⇔−− −++−− −++−− −+=
.
Vì
1x ≥
;
2y ≥
;
3z ≥
nên ta có
( )
( )
( )
2 22
11 2 2 33 0xy z−−+ −−+ −−=
Suy ra
( )
2
11 0x −− =
và
( )
2
22 0y −− =
và
( )
2
33 0z −− =
Suy ra
11x −=
và
22y −=
và
33z −=
Suy ra
11x −=
và
24y −=
và
39z −=
Suy ra
2x =
và
6y =
và
12z =
(thỏa mãn điều kiện )
Vậy
2x =
và
6y =
và
12z =
.
__________ THCS.TOANMATH.com __________
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÒNG GD VÀ ĐT THỊ XÃ SƠN TÂY
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
TRƯỜNG THCS SƠN ĐÔNG NĂM HỌC 2019 - 2020 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề) ĐỀ 1 Bài 1. ( 2 điểm) Tính a) 5 12 + 4 27 − 6 48 b) ( 300 − 2 675 + 5 75) : 3 1 1 2 2 c) − d) + 5 − 3 5 + 3 4 − 2 3 4 + 2 3 Bài 2.
(2,0 điểm).Giải phương trình : a) 2x + 3 = 5 ;
b) 5 9x + 9 − 2 4x + 4 + x +1 = 36 . x + 2 Bài 3.
(2,0 điểm).Cho hai biểu thức A = và x −1 x − 2 x − 3 x − 6 x − 22 B = + −
(x ≥ 0, x ≠ )1. x + 3 x + 2 x + 5 x + 6
a) Tính giá trị của biểu thức A tại x = 25 . x + 3 b) Chứng minh B = . x + 2
c) Tìm tất cả các giá trị nguyên của x để P = .
A B có giá trị nguyên. Bài 4. (3,5 điểm)
1) Một cột đèn có bóng trên mặt đất dài 6m. Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 0
40 . Tính chiều cao của cột đèn (làm tròn đến mét).
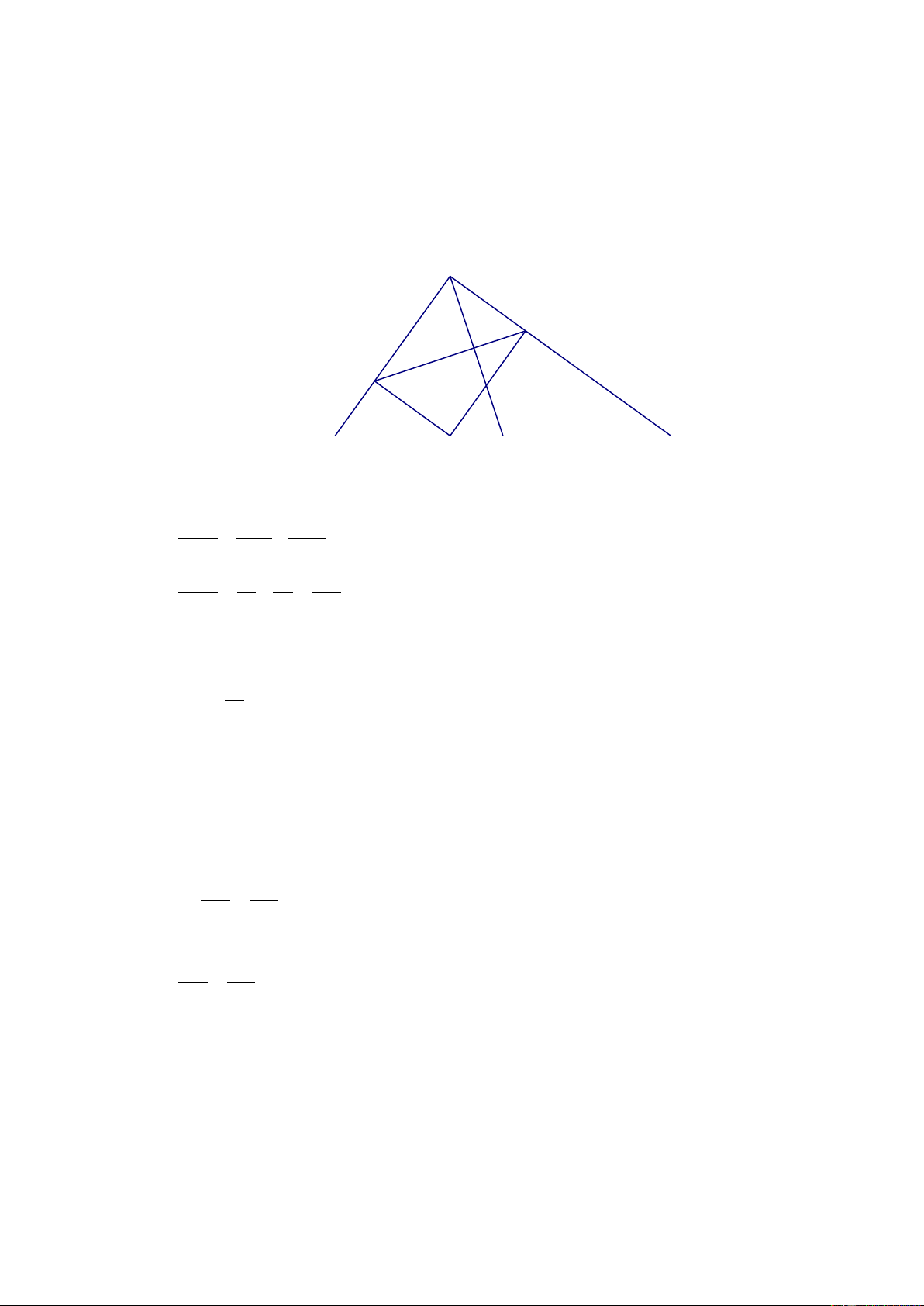
2) Cho tam giác ABC vuông tại A , đường cao AH . Biết AB = 3c , m AC = 4cm . a) Tính AH
b) Gọi D, E lần lượt là hình chiếu của H trên AB và AC . Chứng minh tam giác AED
và tam giác ABC đồng dạng.
c) Kẻ trung tuyến AM , gọi N là giao điểm của AM và DE . Tính tỉ số diện tích của tam
giác AND và tam giác ABC Bài 5.
(0,5 điểm). Tìm các số x, y , z thỏa mãn đẳng thức:
x + y + z + 8 = 2 x −1 + 4 y − 2 + 6 z − 3 HẾT
PHÒNG GD VÀ ĐT THỊ XÃ SƠN TÂY
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
TRƯỜNG THCS SƠN ĐÔNG NĂM HỌC 2019 - 2020 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề) ĐỀ 1
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1. a) 5 12 + 4 27 − 6 48 2 2 2 = 5 2 .3 + 4 3 .3 − 6 4 .3 = 5.2 3 + 4.3 3 − 6.4 3 =10 3 +12 3 − 24 3 = 2 − 3 b) ( 300 − 2 675 + 5 75) : 3 = ( 2 2 2
10 .3 − 2 15 .3 + 5 5 .3 ) : 3 = (10 3 − 2.15 3 +5.5 3): 3 = (10 −30 + 25) 3 : 3 = 5 3 : 3 = 5 1 1 c) − 5 − 3 5 + 3 ( 5+ 3)−( 5− 3) = ( 5+ 3)( 5− 3) 5 + 3 − 5 + 3 = 2 3 = = 3 5 − 3 2 2 2 d) + 4 − 2 3 4 + 2 3 2 (4 + 2 3) + 2(4 − 2 3) = (4−2 3)(4+2 3) 8 + 4 3 + 8 − 4 3 = 4 − (2 3)2 2 16 = 16 = = 4 16 −12 4 Bài 2. a) Điề 3 − u kiện: x ≥ 2
2x + 3 = 5 ⇔ 2x + 3 = 25 ⇔ x = 11 (nhận)
Vậy nghiệm của phương trình là: x = 11
b) Điều kiện: x ≥ 1 −
5 9x + 9 − 2 4x + 4 +
x +1 = 36 ⇔ 15 x +1 − 4 x +1 + x +1 = 36
⇔ 12 x +1 = 36 ⇔ x +1 = 3 ⇔ x +1 = 9 ⇔ x = 8 (nhận)
Vậy nghiệm của phương trình x = 8 Bài 3. 25 + 2 7
a) Tại x = 25 , ta được: A = = . 25 −1 4 x − 2 x − 3 x − 6 x − 22 B = + −
( x ≥ 0, x ≠ ) 1 x + 3 x + 2 x + 5 x + 6 − + − − + + + + ( x + x x x x x x )2 3 4 9 6 22 6 9 x + 3 = ( = = = . x + 3)( x + 2)
( x +3)( x +2) ( x +3)( x +2) x +2 x + 2 x + 3 x + 3 4 b) P = . A B = . = =1+ x −1 x + 2 x −1 x −1 Để 4 P = .
A B có giá trị nguyên thì nguyên x −1 ⇒ 4( x − ) 1 ⇒ ( x − ) 1 ∈U (4) = { 4, − 2, − 1 − ,1, 2, } 4 Khi đó: x −1 = 4 − ⇒ x = 3 − (loại) x −1 = 2 − ⇒ x = 1 − (loại) x −1 = 1
− ⇒ x = 0 (thỏa mãn) x −1 = 1 ⇒
x = 2 ⇒ x = 4 (thỏa mãn) x −1 = 2 ⇒
x = 3 ⇒ x = 9 (thỏa mãn) x −1 = 4 ⇒
x = 5 ⇒ x = 25 (thỏa mãn) Vậy x ∈{0, 4,9, 2 } 5 . B Bài 4. 1) Gọi
AB là chiều cao cột đèn.
AC là độ dài bóng của cột đèn
Góc C là góc tạo bởi tia nắng mặt trời với mặt 40° đất. A 6m C Xét A
∆ BC vuông tại A :
AB = AC. tan C ( hệ thức cạnh và góc trong tam giác vuông) 0 AB = 6. tan 40 ≈ 5 m
Vậy, chiều cao cột đèn xấp xỉ 5 m. 2) A E N O D B H M C a) Xét A
∆ BC vuông tại A , đường cao AH : 1 1 1 = +
( hệ thức lượng trong tam giác vuông ) 2 2 2 AH AB AC 1 1 1 25 = + = 2 2 2 AH 3 4 144 144 2 AH = 25 12 AH = (cm) 5 b) Xét A
∆ BH vuông tại H , đường cao HE : 2 AH = A .
D AB ( hệ thức lượng trong tam giác vuông) Xét A
∆ HC vuông tại H , đường cao HD 2
AH = AE.AC ( hệ thức lượng trong tam giác vuông) ⇒ A .
D AB = AE.AC AD AE ⇒ = AC AB Xét A ∆ DE và A ∆ CB : AD AE = (chứng minh trên) AC ABBAC chung ⇒ A ∆ DE ” A ∆ CB (c-g-c) c) Xét A
∆ BC vuông tại A , đường trung tuyến AM
⇒ AM = MB = MC
MA = MC ⇒ A
∆ MC cân tại M ⇒  =  MAE MCA MA = MB ⇒ A
∆ MB cân tại M ⇒  =  NAD ABC Có :  =  OAE OEA Mà  =  OAE ABH ( cùng phụ  OAD ) ⇒  =  ABH OEA Có :  +  ABH ACB = 90° ⇒  +  NAE NEA = 90° ⇒  ANE = 90° Xét A ∆ ND và B ∆ AC :  =  AND BAC = 90°  =  NAD ABC ⇒ A ∆ ND ” B ∆ AC (g-g) 2 SAD AND ⇒ =   SBC BAC Có A
∆ HB vuông tại H , đường cao HD : 2 AH = A . D AB 2 2 AH 2, 4 ⇒ AD = = = 1,92 (cm) AB 3 2 2 SAD  1,92  AND ⇒ = = = 0, 4096     SBC   3  BAC Bài 5.
(0,5 điểm). Tìm các số x, y , z thỏa mãn đẳng thức:
x + y + z + 8 = 2 x −1 + 4 y − 2 + 6 z − 3 Lời giải
Điều kiện : x ≥1 ; y ≥ 2 ; z ≥ 3
x + y + z + 8 = 2 x −1 + 4 y − 2 + 6 z − 3
⇔ x −1− 2 x −1 +1+ y − 2 − 4 y − 2 + 4 + z − 3 − 6 z − 3 + 9 = 0 .
Vì x ≥ 1; y ≥ 2 ; z ≥ 3 nên ta có
( x− − )2 +( y− − )2 +( z− − )2 1 1 2 2 3 3 = 0 Suy ra ( x − − )2 1 1 = 0 và ( y − − )2 2 2 = 0 và ( z − − )2 3 3 = 0 Suy ra x −1 = 1 và y − 2 = 2 và z − 3 = 3
Suy ra x −1 = 1 và y − 2 = 4 và z − 3 = 9
Suy ra x = 2 và y = 6 và z = 12 (thỏa mãn điều kiện )
Vậy x = 2 và y = 6 và z = 12 .
__________ THCS.TOANMATH.com __________