Đề thi giữa kì 1 Toán 9 năm 2020 – 2021 trường THCS Thăng Long – Hà Nội

Nhằm kiểm tra đánh giá chất lượng dạy và học môn Toán lớp 9 định kỳ, ngày … tháng 11 năm 2020, trường THCS Thăng Long, quận Ba Đình, thành phố Hà Nội tổ chức kỳ thi kiểm tra chất lượng giữa học kỳ 1 môn Toán 9 năm học 2020 – 2021. Mời bạn đọc đón xem.

39 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 9

Môn: Toán 9

Thông tin:

6 trang 9 tháng trước

Tác giả:

Profile Hà Việt Anh
PHÒNG GD VÀ ĐT QUẬN BA ĐÌNH
TRƯỜNG THCS THĂNG LONG
-
---------
THCS.TOANMATH.com
Bài 1: Rút gọn các biểu thức sau:
a)
1
2 18 50 32
5
A
b)
2 3 3 23 3 1
23
31 3
B


c)
sin54 cot54 sin36C 
Bài 2: Giải các phương trình sau:
a)
5 5 9 45 4 20 12 0xx x
b)
2
6 946xx 
c)
2
1 10xx
Bài 3: Với
0x
và
4x
cho hai biểu thức:
và
34
4
22
xx
B
x
xx


a) tính giá trị của biểu thức
A
khi
25x
.
b) Rút gọn biểu thức
B
.
c) Tìm
x
để
.1AB
.
Bài 4: Cho tam giác
ABC
vuông tại
A
có
30C 
a) Biết
10BC
cm. Giải tam giác vuông
ABC
b) Trên tia
BA
lấy điểm
I
sao cho
2BI BC
. Chứng minh rằng tam giác
BAC
đồng
dạng với
BIC
. Từ đó chứng minh rằng
2 22
1 11
CA CB CI

.
c) Lấy
M
là trung điểm của
BI
. Chứng minh
2. .CACM CB CI
Bài 5: Một người đứng trên một đỉnh tháp cao 300 m
nhìn xuống hai đầu cầu A và B với góc tạo với
phương ngang lần lượt là
28
và
20
. Hãy tính:
a) Khoảng cách từ chân cầu A đến chân tháp ?
b) Chiều dài cây cầu AB? ( Làm tròn các kết
quả đến chữ số thập phân thứ hai )
Bài 6: Cho
23x
. Tìm giá trị nhỏ nhất của biểu
thức:

22
11 1
23
23
M
xx
xx



HẾT
x
28
°
20
°
300m
C
H
B
A
ĐỀ
KIỂM TRA GIỮA HỌC KỲ 1
NĂM HỌC 2020 - 2021
MÔN TOÁN - LỚP 9
Thời gian làm bài: 90 phút (không kể th
ời gian giao đề)
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. a)
1
2 18 50 32
5
A
1
2 9.2 25.2 16.2
5
A
1
2.3 2 .5 2 4 2
5
A
62 2 42A 
92A
b)
2 3 3 23 3 1
23
31 3
B


2 3 3 23 3
3 1 3 23
B


2 3. 2 3 2 3 1 . 3 2 3 3. 3 1
23.31 2 31.3 23.31
B



2.333623
43 6 33
3
6 23 6 23 6 23
B




43 6 63 6 12 43 33 3
6 23
B
 
33
6 23
B

3 36 23
6 23 6 23
B


2
63 18 6 63
36 2 3
B

12
36 12
B
1
2
B
c)
sin54 cot54 sin36C 
PHÒNG GD VÀ ĐT QUẬN BA ĐÌNH
TRƯỜNG THCS THĂNG LONG
-
---------
THCS.TOANMATH.com
ĐỀ
KIỂM TRA GIỮA HỌC KỲ 1
NĂM HỌC 2020 - 2021
MÔN TOÁN - LỚP 9
Thời gian làm bài: 90 phút (không kể th
ời gian giao đề)
cos54
sin54 . sin36
sin54
C

cos54 sin36C 
sin36 sin36C 
0C
Câu 2. a)
5 5 9 45 4 20 12 0xx x
5x 
5 53 52 512xxx 
4 5 12x 
53x 
59x
4x
(nhận)
Vậy
4S
b)
2
6 946xx 
2
32x 
32x
32
32
x
x


5
1
x
x
Vậy
1; 5S
c)
2
1 10xx
1x
2
11xx 
2
11xx 
2
0xx 
10xx 
1x
(nhận) hoặc
0x
(loại)
Vậy
1S
Câu 3. a) Với
25x
, ta được:
25 2 7
8
25 3
A

.
b)
34
4
22
xx
B
x
xx


Với
0x
và
4x
, ta được:
34
4
22
xx
B
x
xx


2 32
4
22 22 22
xx x
x
xx xx xx


  

52
5
2
22
x
x
xx


.
c) Vì
.1AB
nên
25 5 2
. 1 10 0
32 3 3
xx
xx x x



20
30 0
2
4
20
30
x
xx
x
x
x
x
x voli






Kết hợp điều kiện
0x
và
4x
, ta có
04x
.
Câu 4.
a) Tam giác
ABC
vuông tại
A
có :
90BC
90BC 
90 30 
60
Áp dụng hệ thức giữa cạnh và góc ta có :
sinAB BC C
10sin30
1
10.
2
5
(cm)
sinAC BC B
10sin60
3
10.
2
53
(cm)
Vậy tam giác
ABC
có
90A
;
30C 
;
60B 
;
5AB
cm ;
53AC
cm ;
10BC
cm
b) Xét
BAC
và
BIC
có :
ABC IBC
1
2
AB BC
BC BI

M
I
B
A
C
Do đó
ABC CBI#
( c – g – c )
Suy ra
ICB CAB
90
Xét
CBI
vuông tại
C
có
CA
là đường cao. Áp dụng hệ thức giữa cạnh và đường cao
ta có
2 22
1 11
CA CB CI

c) Xét
CBI
vuông tại
C
có
CA
là đường cao. Áp dụng hệ thức giữa cạnh và đường
cao ta có
..CI BC CA BI
1
Mặt khác
CBI
vuông tại
C
có
CM
là đường trung tuyến ứng với cạnh huyền
BI
nên
2BI CM
2
Từ
1
và
2
ta có
. .2CI BC CA CM
hay
2. .CACM CI BC
Câu 5.
a) Ta có :
Cx HB//
28xCA HAC 
Xét
CHA
vuông tại
H
:
tan
CH
HAC
HA
0
300
546,22
tan 28
tan
CH
HA
HAC

m
Vậy, khoảng cách từ chân cầu A đến chân tháp xấp xỉ
546,22
m
b) Xét
CHB
vuông tại
H
:
tan
CH
HBC
HB
300
824,24
tan 20
tan
CH
HB
HBC

m
824,24 546,22 278,02AB HB HA
m
Vậy, chiều dài cây cầu AB xấp xỉ
278,02
m
Câu 6. Với
23x
ta có:
( ) ( )
( )( )
22
11 1
23
23
M
xx
xx
=++
−−
−−
x
28
°
20
°
300m
C
H
B
A
( )( ) ( )( )
21
23 23xxxx
≥+
−− −−
( )( )
3
23xx
=
−−
Mà

2
2
11
2 3 5
6 2,5
44
x x xx x 
Nên
33
12
1
23
4
xx


Dấu “=” xảy ra khi :
11
23
2,5 0
xx
x


23
2,5
xx
x

2,5x
(nhận)
Khi đó
min
12M
.
Vậy giá trị nhỏ nhất của M bằng 12 khi
2,5x
__________ THCS.TOANMATH.com __________
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

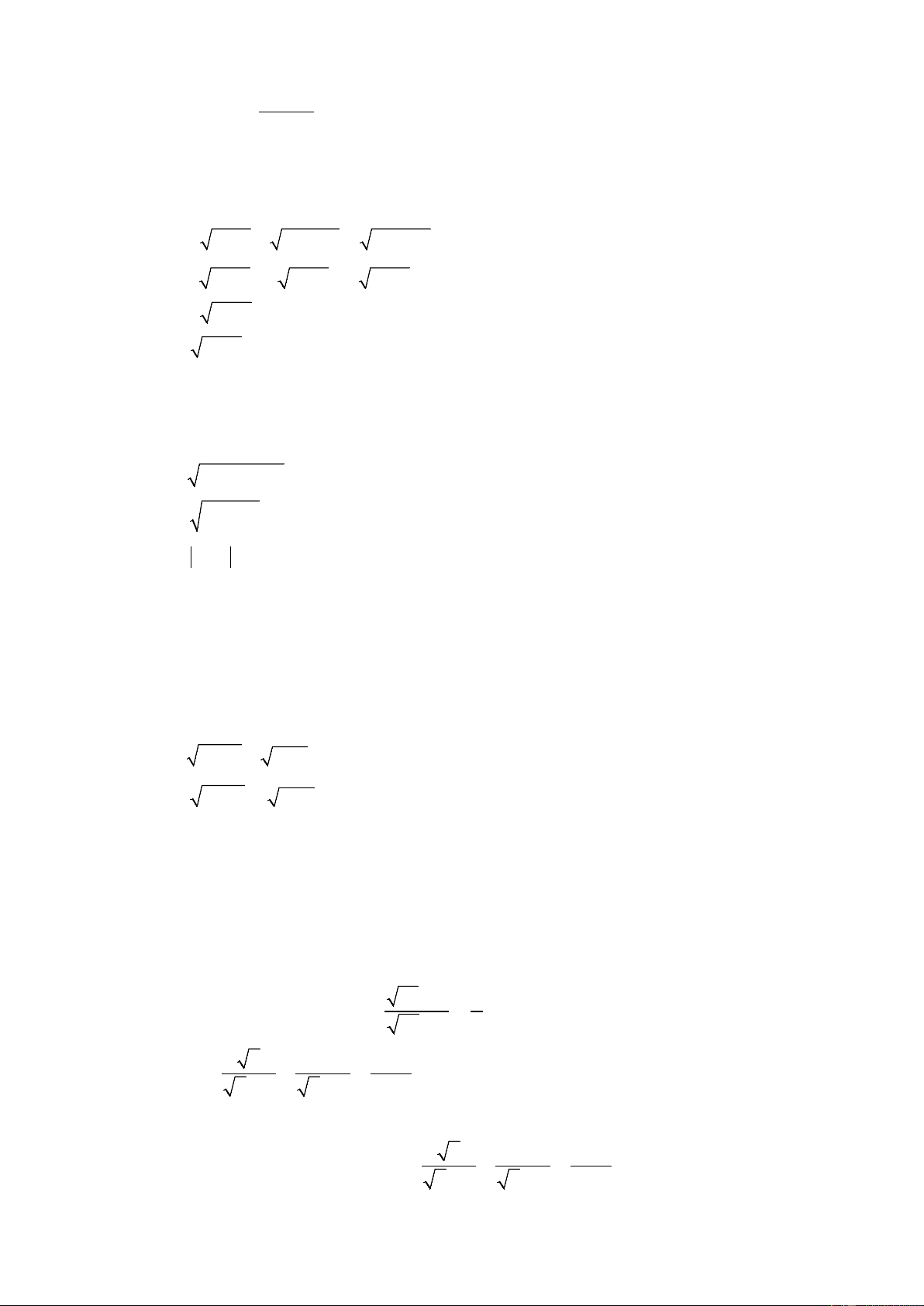
Preview text:

PHÒNG GD VÀ ĐT QUẬN BA ĐÌNH
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
TRƯỜNG THCS THĂNG LONG NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
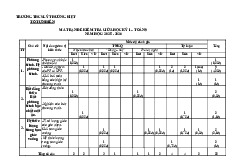
Thời gian làm bài: 90 phút (không kể thời gian giao đề) Bài 1:
Rút gọn các biểu thức sau: 1 a) A  2 18  50  32 5 2  3 3  2 3 3 1 b) B    3 1 3 2 3
c) C  sin 54 cot 54sin 36 Bài 2:
Giải các phương trình sau:
a) 5 x  5  9x  45  4x  20 12  0 b) 2
x  6x  9  4  6 c) 2
x 1  x 1  0 Bài 3:
Với x  0 và x  4 cho hai biểu thức: x  2 x 3 x  4 A  và B    x  3 x  2 x  2 4  x
a) tính giá trị của biểu thức A khi x  25 .
b) Rút gọn biểu thức B . c) Tìm x để . A B 1. Bài 4:
Cho tam giác ABC vuông tại A có  C  30
a) Biết BC 10 cm. Giải tam giác vuông ABC
b) Trên tia BA lấy điểm I sao cho BI  2BC . Chứng minh rằng tam giác BAC đồng 1 1 1 dạng với B
IC . Từ đó chứng minh rằng   . 2 2 2 CA CB CI
c) Lấy M là trung điểm của BI . Chứng minh 2 . CA CM  . CB CI Bài 5:
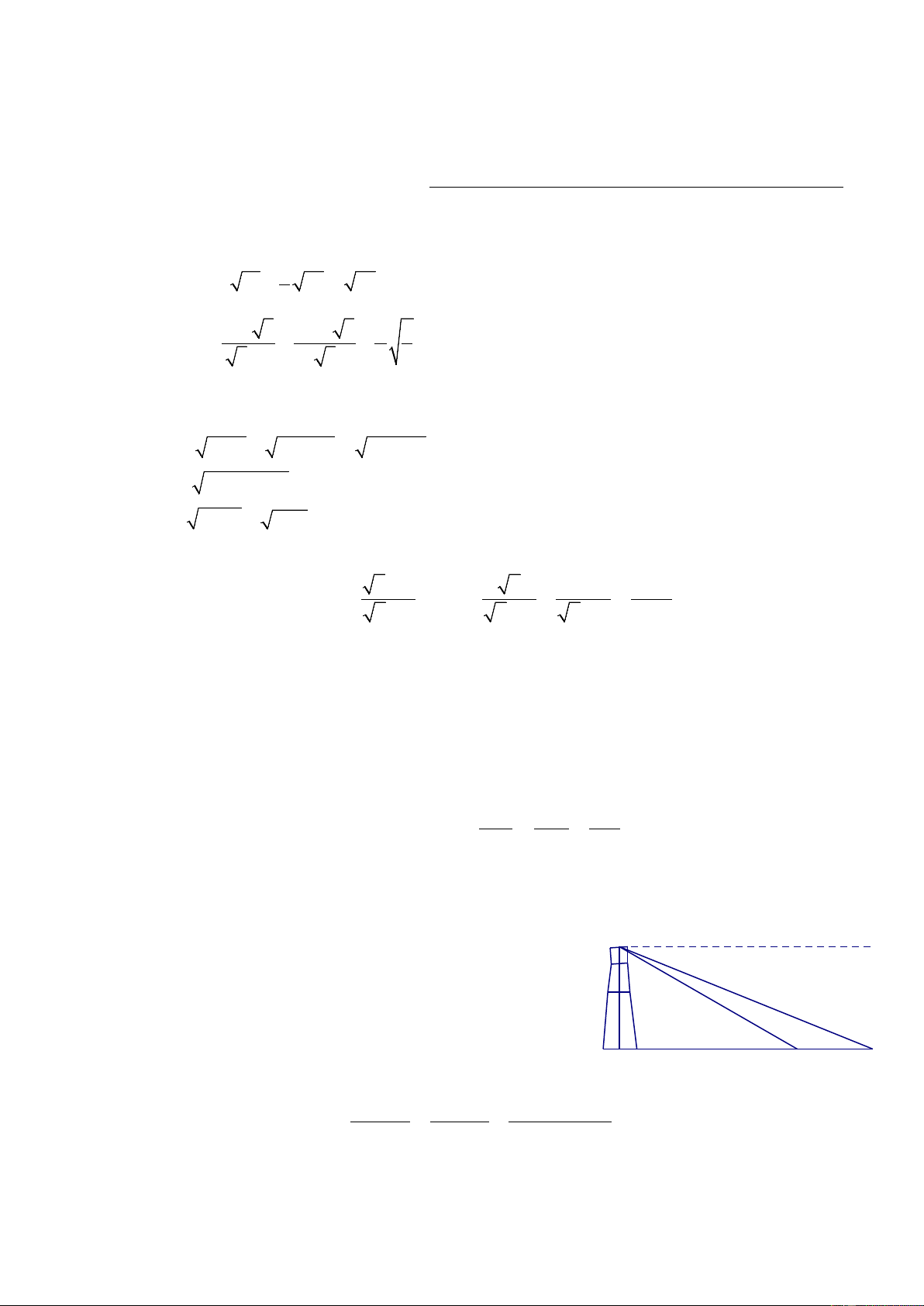
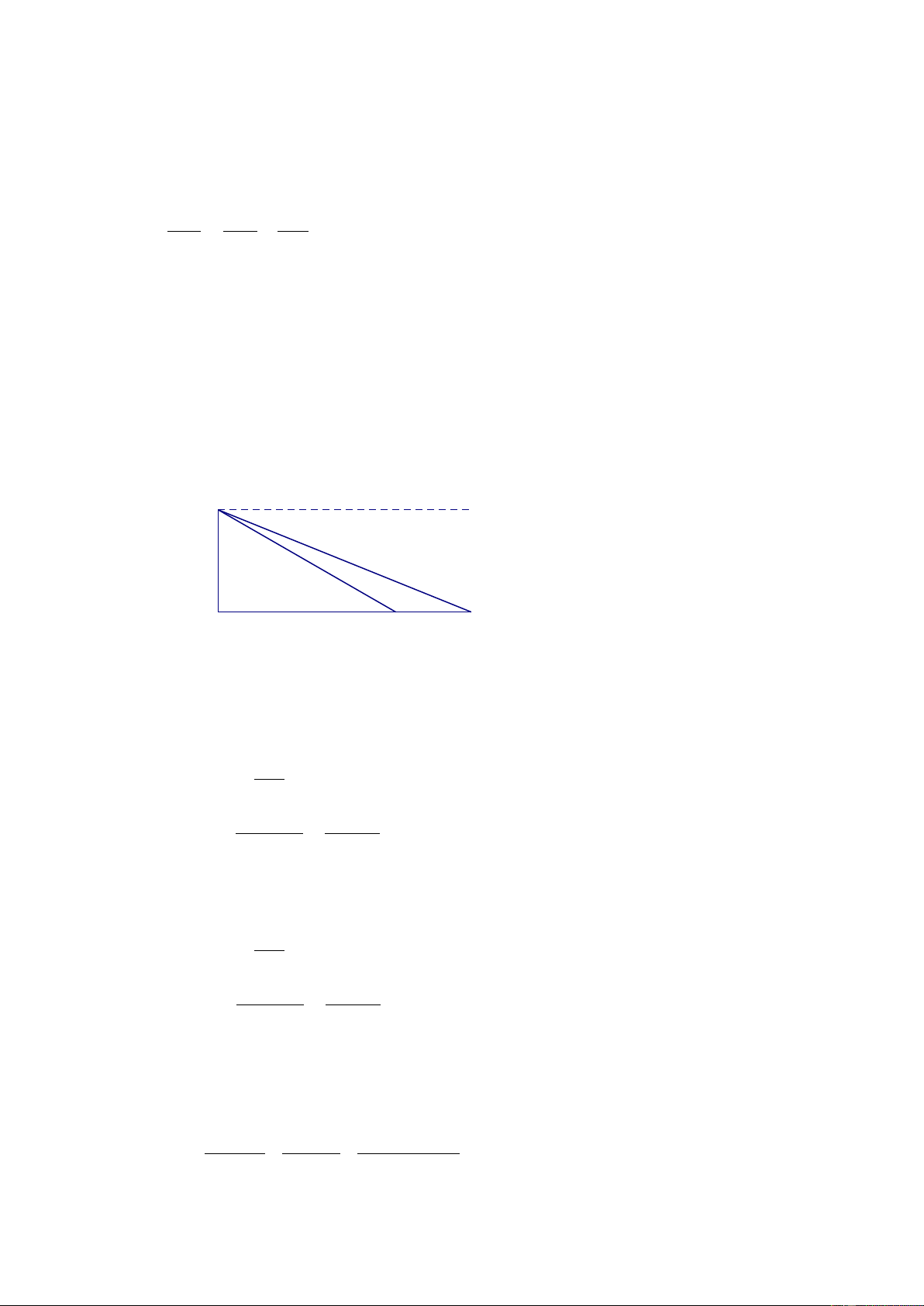
Một người đứng trên một đỉnh tháp cao 300 m
nhìn xuống hai đầu cầu A và B với góc tạo với
phương ngang lần lượt là C x 28 và 20 . Hãy tính: 20°
a) Khoảng cách từ chân cầu A đến chân tháp ? 28°
b) Chiều dài cây cầu AB? ( Làm tròn các kết 300m
quả đến chữ số thập phân thứ hai ) Bài 6:
Cho 2  x  3 . Tìm giá trị nhỏ nhất của biểu H B A thức: 1 1 1 M   
x22 3 x2 x23 x HẾT
PHÒNG GD VÀ ĐT QUẬN BA ĐÌNH
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
TRƯỜNG THCS THĂNG LONG NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
HƯỚNG DẪN GIẢI CHI TIẾT 1 Câu 1. a) A  2 18  50  32 5 1 A  2 9.2  25.2  16.2 5 1
A  2.3 2  .5 2  4 2 5 A  6 2  2  4 2 A  9 2 2  3 3  2 3 3 1 b) B    3 1 3 2 3 2  3 3  2 3 3 B    3 1 3 2 3 2  3. 2  3 2 3   1  . 3  2 3 3. 3   1 B    2 3  . 3   1 2 3   1 . 3 2 3  . 3   1 2  .3 3362 3 4 3 6  3 33 B    6  2 3 6  2 3 6  2 3
4 3  6 6 3  612  4 3 3 3  3 B  6  2 3  3 3 B  62 3  3 362 3
B  62 362 3 6 3 186  6 3 B  36 2 32 12 B  3612 1 B  2
c) C  sin 54 cot 54sin 36 cos 54 C  sin 54. sin 36 sin 54
C  cos 54sin 36
C  sin 36sin 36 C  0 Câu 2.
a) 5 x  5  9x  45  4x  20 12  0 x   5
 5 x 5 3 x 5  2 x 5 12  4 x 5 12  x 5  3  x 5  9  x  4 (nhận) Vậy S    4 b) 2
x  6x  9  4  6  x 2 3  2  x 3  2 x3  2  x32  x  5  x 1  Vậy S  1;  5 c) 2
x 1  x 1  0 x   1 2
x 1  x 1 2
x 1 x1 2
x x  0  xx  1  0
x 1 (nhận) hoặc x  0 (loại) Vậy S    1 25  2 7 Câu 3.
a) Với x  25 , ta được: A   . 25  3 8 x 3 x  4 b) B    x  2 x  2 4  x
Với x  0 và x  4 , ta được: x 3 x  4 B    x  2 x  2 4  x x x   2 3 x   2 x  4     x   2  x   2
x  2 x  2  x  2 x  2 5 x   2 5    . x   2  x   2 x  2 c) Vì . A B 1 nên x  2 5 5 2  x . 1  1 0   0 x  3 x  2 x  3 x  3 2 x  0 
 x30x0   x  2      x  4   2 0 x x     
 x 30voli  
Kết hợp điều kiện x  0 và x  4 , ta có 0  x  4 . Câu 4. C I M A B
a) Tam giác ABC vuông tại A có :  
B C  90  
B  90C  9030  60
Áp dụng hệ thức giữa cạnh và góc ta có : 1
AB BC sin C  10 sin 30  10.  5 (cm) 2 3
AC BC sin B  10 sin 60 10.  5 3 (cm) 2
Vậy tam giác ABC có  A  90 ;  C  30 ; 
B  60 ; AB  5 cm ; AC  5 3 cm ; BC  10 cm b) Xét BAC và BIC có :   ABC IBC AB BC 1   BC BI 2 Do đó ABC # C
BI ( c – g – c ) Suy ra  
ICB CAB  90 Xét C
BI vuông tại C có CA là đường cao. Áp dụng hệ thức giữa cạnh và đường cao ta có 1 1 1   2 2 2 CA CB CI c) Xét C
BI vuông tại C có CA là đường cao. Áp dụng hệ thức giữa cạnh và đường cao ta có
CI.BC C . A BI   1 Mặt khác C
BI vuông tại C có CM là đường trung tuyến ứng với cạnh huyền BI nên
BI  2CM 2 Từ  
1 và 2 ta có CI.BC  .2 CA CM hay 2 .
CA CM CI.BC Câu 5. C x 20°28° 300m H B A
a) Ta có : Cx // HB  
xCA HAC  28 Xét C
HA vuông tại H :  CH tan HAC HA CH 300  HA     546, 22 m 0 tan HAC tan 28
Vậy, khoảng cách từ chân cầu A đến chân tháp xấp xỉ 546,22 m b) Xét C
HB vuông tại H :  CH tan HBC HB CH 300  HB     824, 24 m tan HBC tan 20
AB HB HA  824, 24546, 22  278,02 m
Vậy, chiều dài cây cầu AB xấp xỉ 278,02 m Câu 6.
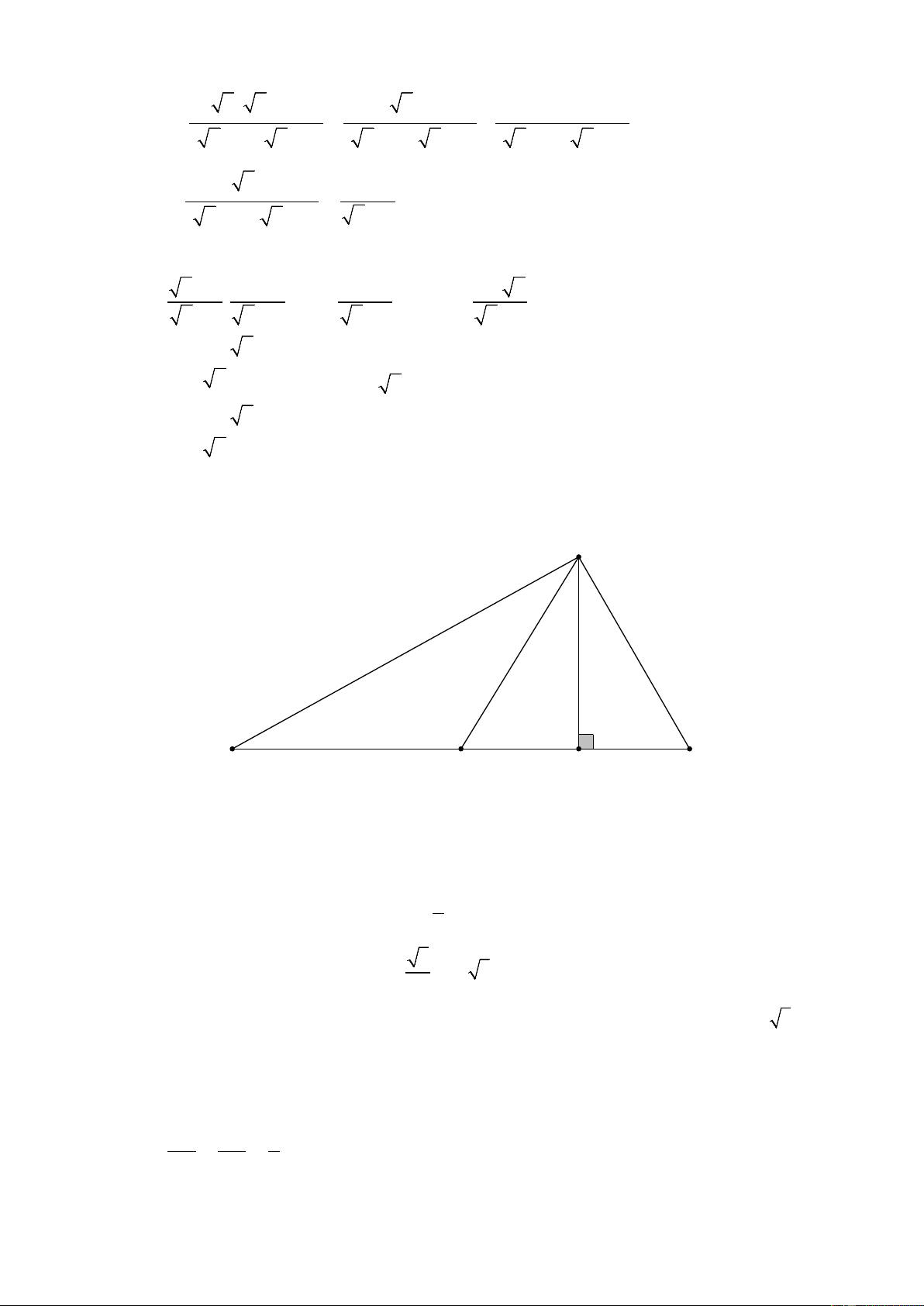
Với 2  x  3 ta có: 1 1 1 M = + +
(x − 2)2 (3− x)2 (x − 2)(3− x) 2 1 ≥ ( +
x − 2)(3 − x) ( x − 2)(3 − x) 3
= (x−2)(3− x) 1 1
Mà x  23 x  x  5x 6  x  2, 2 2 5  4 4 3 3 Nên   
x  23 x 12 1 4 Dấu “=” xảy ra khi :  1 1  
x2 3x
x2, 50 
x2  3 x   x2,5   x  2,5 (nhận) Khi đó M 12 . min
Vậy giá trị nhỏ nhất của M bằng 12 khi x  2,5
__________ THCS.TOANMATH.com __________