

Preview text:
TRƯỜNG THCS THÀNH CÔNG
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 ---------- NĂM HỌC 2020 - 2021 THCS.TOANMATH.com MÔN TOÁN - LỚP 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề) Bài 1:
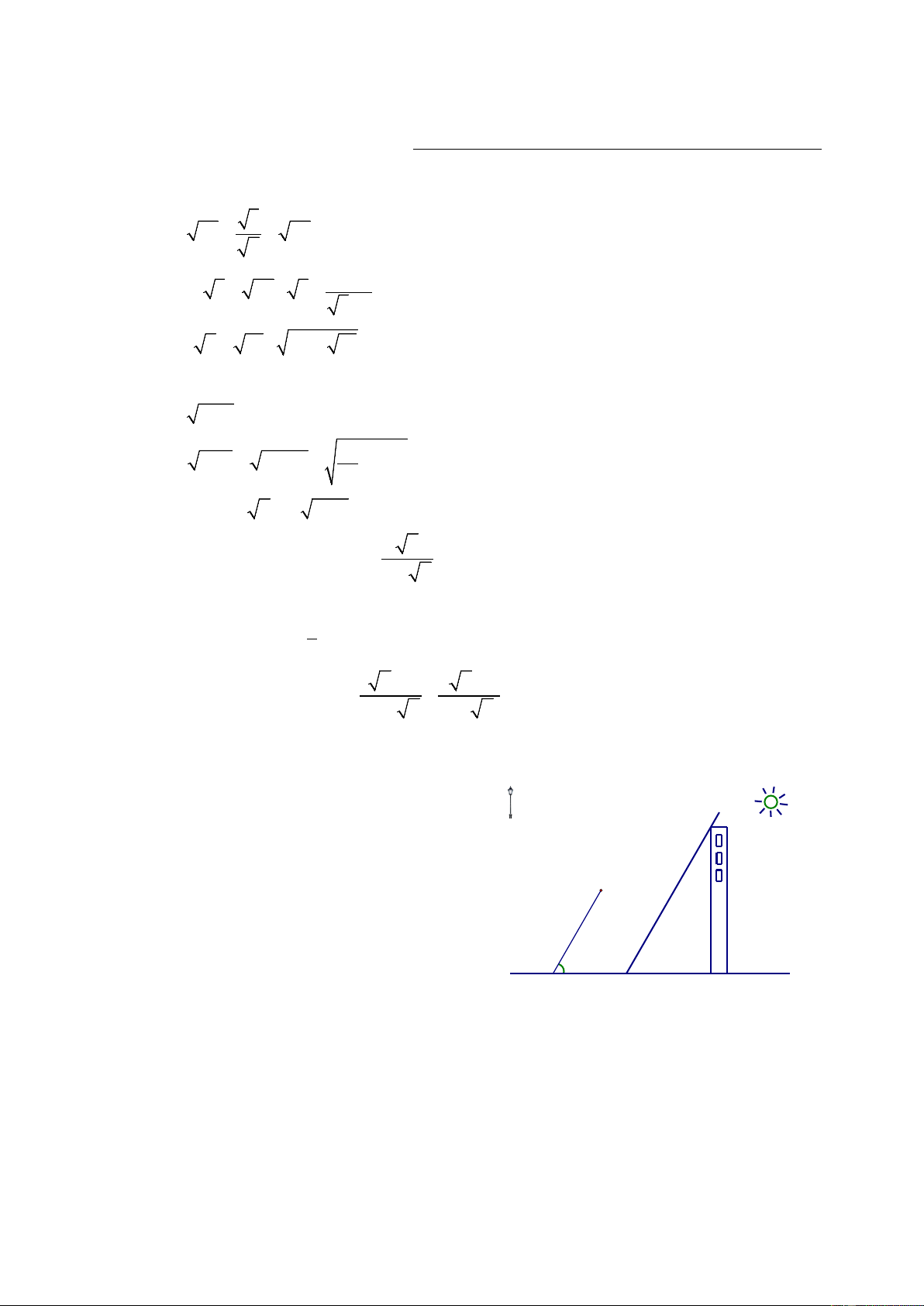
(2 điểm) Thực hiện phép tính: 8 a) 3 25 + + 27 2 b) ( − ) 2 5 3 27 . 3 + 3 −1 c) ( 6 + 10 ). 8 − 2. 15 Bài 2:
(2 điểm) Giải phương trình: a) x − 3 = 2 9
b) x −1 + 4x − 4 − (x − )1 = 3 25
c) 9 + x − 6 x = − x − 9 x Bài 3:
(2 điểm) Cho biểu thức A =
với x ≥ 0 và x ≠ 4 . 2 − x
a) Tính giá trị của A khi x = 9 . 1
b) Tìm x biết A = . 3 x −1 2 x + 2
c) Cho biểu thức B = A : −
. Tìm m để phương trình B = m có x − 2 x x + x nghiệm. Bài 4:
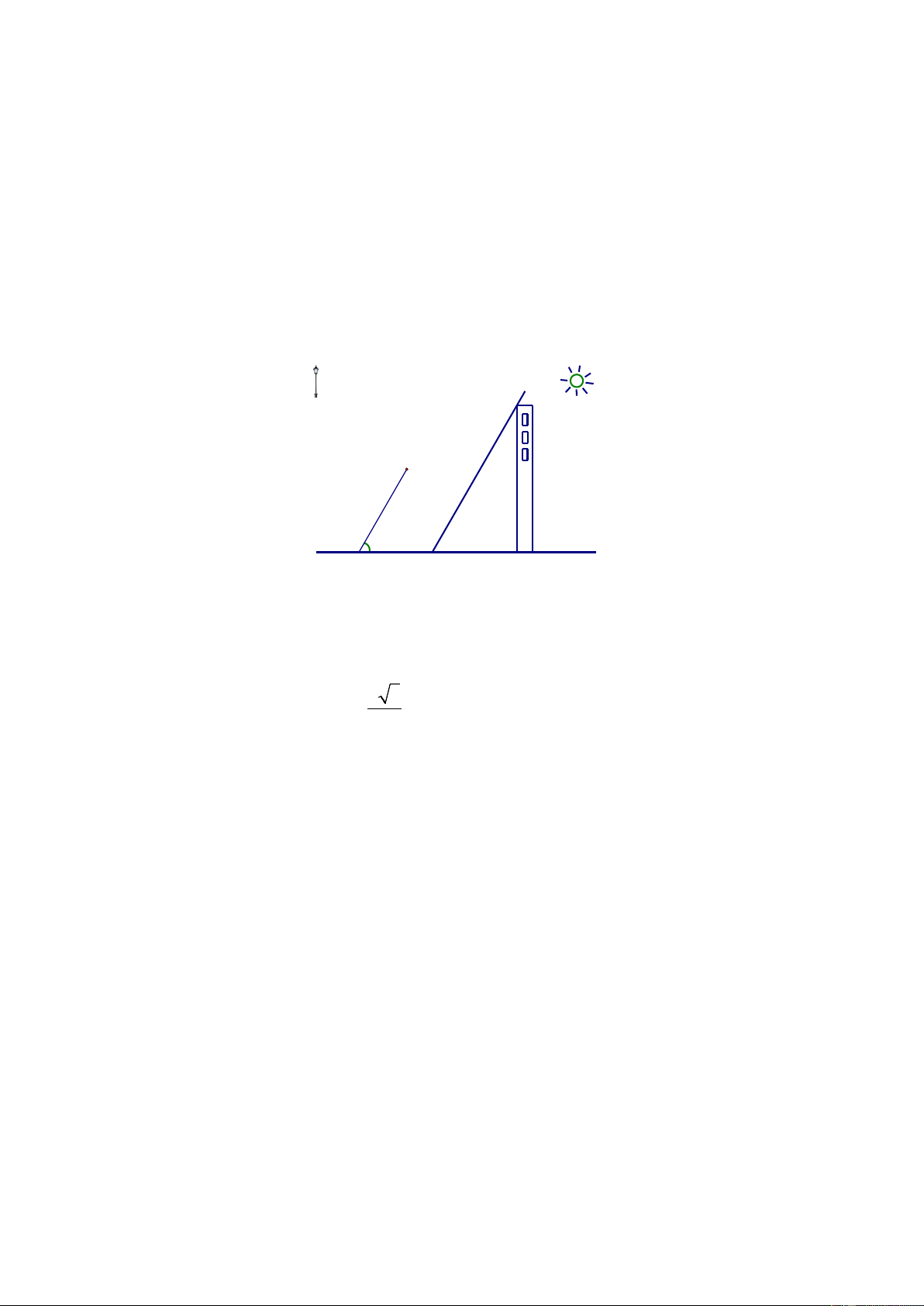
(1,5 điểm) Các tia nắng mặt trời tạo với mặt đất một góc bằng 60°.
a) Tính độ dài bóng của một cột đèn trên
mặt đất (Làm tròn đến mét ), biết cột đèn cao 7 m.
b) Tại thời điểm đó, gần cột đèn có một tòa
nhà cao tầng có bóng trên mặt đất bằng
86, 7 m. Tính số tầng của tòa nhà, biết mỗi 7m
tầng cao khoảng 3 m. (Coi như các tia sáng 60° 86,7m
mặt trời là các đường thẳng song song). Bài 5: (2,5 điểm) Cho A
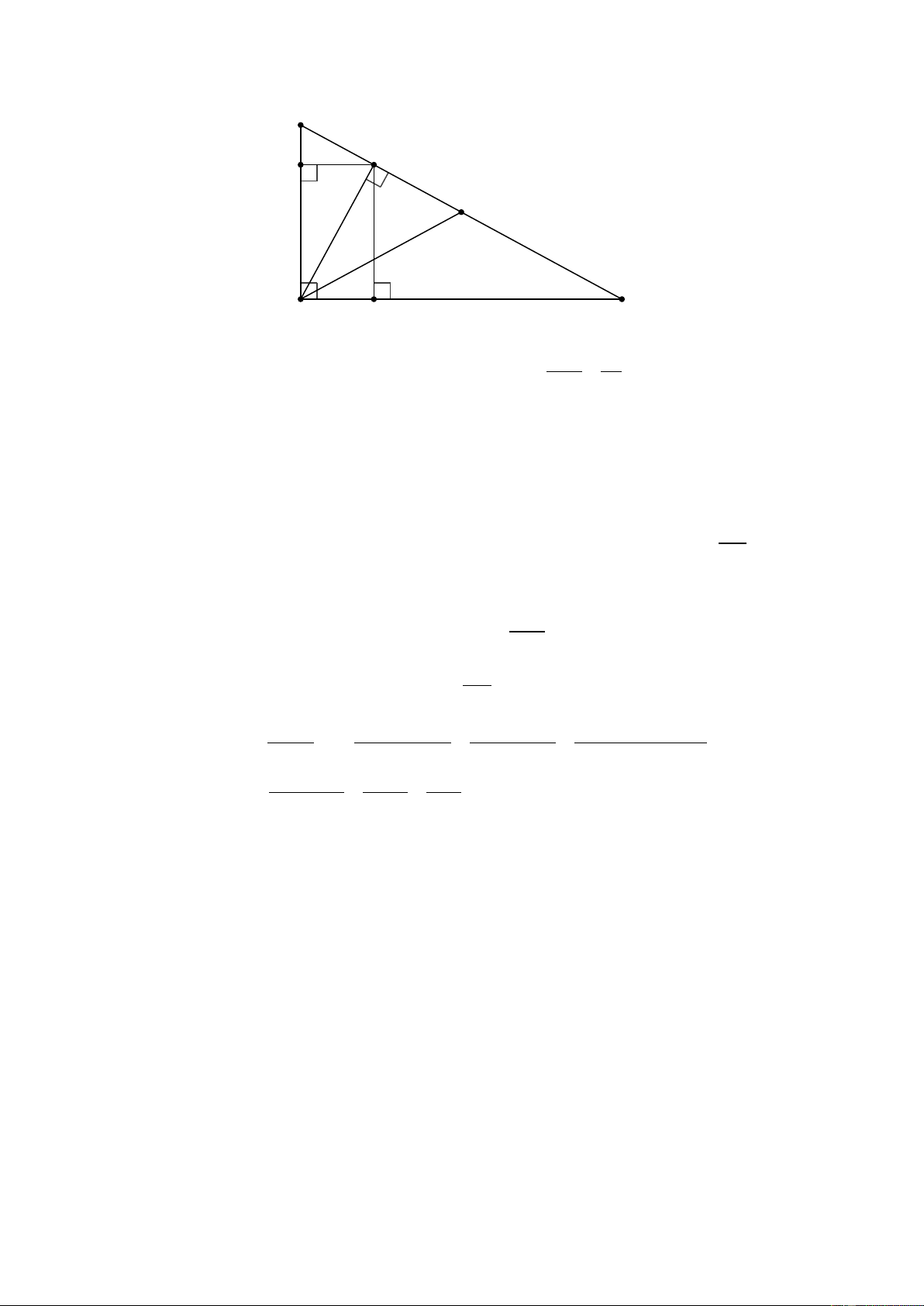
∆ BC vuông tại A có AB < AC , đường cao AH .
a) Cho AB = 5cm , BC = 13cm . Tính BH (làm tròn đến chữ số thập phân thứ ba).
b) Kẻ HD ⊥ AB , HE ⊥ AC . Chứng minh: A .
D AB = AE.AC . c) Nếu ACB < 45° và
ACB = α . Chứng minh: 2 2 cos α −1 = cos 2α .
__________ THCS.TOANMATH.com __________
HƯỚNG DẪN GIẢI CHI TIẾT 8 Bài 1: a) 3 25 + + 27 2 = 5 + 2 + 3 = 10 b) ( − ) 2 5 3 27 . 3 + 3 −1 = ( − ) 2.( 3 + ) 1 5 3 3 3 . 3 + = (15 − 9) + 3 +1 = 7 + 3 3 −1 c) ( 6 + 10 ). 8 − 2. 15 = ( + ) ( − )2 2 3 5 . 5 3 = 2 ( 3 + 5)( 5 − 3) = 2.(5 − 3) = 2 2 Bài 2:
a) x − 3 = 2 (điều kiện x 3 ) ⇔ x − 3 = 4
⇔ x = 7 thỏa mãn điều kiện
Vậy phương trình đã cho có nghiệm: x = 7 9
b) x −1 + 4x − 4 −
(x − )1 = 3 (điều kiện: x ≥1) 25 ⇔ 3
x −1 + 2 x −1 − x −1 = 3 5 ⇔ 12 x −1 = 3 5 ⇔ 5 x −1 = 4 ⇔ 25 x −1 = 16 ⇔ 41 x = (thỏa mãn điều kiện) 16 41
Vậy phương trình đã cho có nghiệm: x = . 16
c) 9 + x − 6 x = − x − 9 (điều kiện: x ≥ 9 ) ⇔ ( x − )2 3 + x − 9 = 0 − = ⇔ x 3 0 x − 9 = 0
⇔ x = 9 (thỏa mãn điều kiện)
Vậy phương trình đã cho có nghiệm: x = 9 . Bài 3:
a) Thay x = 9 (thỏa mãn điều kiện) vào A ta được. 9 3 A = = = 3 − 2 − 9 2 − 3 1 x x 1 3 x − 2 + x b) Ta có A = 1 ⇔ = ⇔ − = 0 ⇔ = 0 3 2 − x 3 2 − x 3 3(2 − x ) 4 x − 2 1 1 ⇔ = ⇒ x − =
⇔ x = ⇔ x = (thỏa mãn điều kiện) 3(2 − x ) 0 4 2 0 2 4 1 1 Vậy x = thì A = 4 3 2 − ( x + x x ) x −1 2 x + 2 1 1
c) Ta có B = A : − = − : x − 2 x x + x
2 − x x ( x − 2) x ( x + )1 x −1− 2 − x ( x 2) x x −1 2 = : − = : 2 − x x 2 − x x ( x − 2)
( x −2) x x (2 − x x ) x 3 − x = x : = . =
, với x ≥ 0 và x ≠ 4 , x ≠ 9 . 2 − x
x ( x − 2) 2 − x ( x −3) x − 3 x Ta có
= m ⇔ x − m x + 3m = 0 (1) x − 3
Đặt x = t (t ≥ 0), ta có phương trình ( ) 1 trở thành: 2
t − mt + 3m = 0 (2) Có 2
∆ = m −12m = m(m −12)
Để phương trình (1) có nghiệm thì phương trình (2) có nghiệm t ≥ 0 , t ≠ 2 , t ≠ 3
Khi đó, ta có các trường hợp sau:
*TH1: Phương trình có nghiệm là 0 , ta có 2 0 − .0
m + 3m = 0 ⇔ m = 0
*TH2: Phương trình có nghiệm bằng 2 và một nghiệm không âm khác 3.
Phương trình (2) có nghiệm bằng 2 ⇔ 4 − .2
m + 3m = 0 ⇔ m = 4 −
Khi đó phương trình (2) có nghiệm thứ 2 là: t = 6
− (không thỏa mãn điều kiện) ⇒ m = 4 − (loại)
*TH3: Phương trình có một nghiệm bằng 3 và một nghiệm không âm khác 2.
Phương trình (2) có nghiệm bằng 3 ⇔ 9 − .3
m + 3m = 0 ⇔ 9 = 0 (vô lý)
⇒ không có giá trị của m thỏa mãn.
*TH4: Phương trình có hai nghiệm trái dấu khác 2; 3, ta có 1.3 m < 0 m < 0 4 − .2
m + 3m ≠ 0 ⇔ m ≠ 4 − 9 − .3 m + 3m ≠ 0
*TH5: Phương trình có hai nghiệm dương khác 2; 3, ta có ∆ ≥ 0 m ≥12 m > 0 m ≤ 0 3 m > 0
⇔ m > 0 ⇔ m ≥12 4 − .2 m + 3m ≠ 0 m ≠ 4 − 9 − .3 m + 3m ≠ 0 m ≤ 0
Vậy m ≥ 12 thì phương trình B = m có nghiệm. m ≠ 4 − Bài 4: 7m 60° 86,7m
Gọi các điểm như hình vẽ:
a) Từ hình vẽ ta thấy bóng cột đèn là đoạn AC . Xét A
∆ BC vuông tại A có: AC = A .
B cot C (Hệ thức lượng trong tam giác vuông) 7 3
Thay số: AC = 7.cot 60° = ≈ 4 (m) 3
Vậy độ dài bóng của một cột đèn trên mặt đất là 4 (m)
b) Do các tia sáng song song với nhau nên EF // BC ⇒ = C
F = 60° (2 góc ở vị trí đồng vị)
Chiều cao của tòa nhà là: ED = F . D tan F
Thay số: ED = 86, 7.tan 60° ED ≈ 150 (m)
Tòa nhà có số tầng là: 150 : 3 = 50 (tầng)
Vậy, tòa nhà đó có 50 tầng. Bài 5: B H D M A C E 2 AB 25 a) A
∆ BC vuông tại A có 2
AB = BH .BC ⇒ BH = = ≈1,923(cm) BC 13 b) A
∆ HB vuông tại H có HD ⊥ AB ⇒ 2 AH = A . D AE A
∆ HC vuông tại H có HE ⊥ AC ⇒ 2
AH = AE.AC ⇒ A .
D AB = AE.AC
c) Lấy M là trung điểm của BC . BC A
∆ BC vuông tại A có AM là đường trung tuyến ⇒ AM = MB = MC = 2 ⇒ MA ∆
C cân tại M ⇒ = AMH 2 ACB = 2α HM A
∆ HM vuông tại H ⇒
cos AMH = cos 2α = AM AC A
∆ BC vuông tại A ⇒ cosC = cosα = BC 2 2 2 2 2 2 AC 2 AC − BC AC − AB
CH .BC − BH .BC 2 2 cos α −1 = −1 = = = 2 2 2 2 BC BC BC BC CH − BH 2HM HM = = = = cos 2α BC 2 AM AM ⇒ 2
2 cos α −1 = cos 2α (đpcm) HẾT




