


Preview text:
TRƯỜNG THCS THANH LIỆT
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 ---------- NĂM HỌC 2020 - 2021 THCS.TOANMATH.com MÔN TOÁN - LỚP 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề) ĐỀ 1 Bài 1:
(2điểm) Tính giá trị của biểu thức:
a) A = 3 8 − 2 18 + 20 3 − 3 2 − 2 b) B = − 3 −1 1− 2 Bài 2:
(1,5 điểm) Giải các phương trình a) 2x −1 = 4 b) 2
4x − 4x +1 = 3 −1 x − 2 x +1 x − 4 x − 9 x + 5 Bài 3:
(2 điểm) Cho các biểu thức P = + + ; Q = với x ≥ 0 , x − 3 x + 3 9 − x 3 − x x ≠ 9 .
a) Tìm giá trị của Q biết x = 1 . x
b) Chứng minh rằng: P = . x − 3
c) Đặt M = P :Q . Tìm giá trị của x để 1 M > . 2 Bài 4:
(1 điểm) Một cây tre bị gẫy ngang thân, ngọn tre vừa chạm đất và tạo với mặt đất một
góc 30° biết khoảng cách từ vị trí ngọn tre chạm đất tới gốc cây là 4,5m . Tính chiều cao
ban đầu của cây tre (làm tròn đến cm). Bài 5:
(3 điểm) Cho tam giác ABC vuông tại A ( AB < AC) . Đường cao AH (H ∈ BC) . Gọi
M và N lần lượt là hình chiếu của H trên AB và AC .
a) Gỉa sử HB = 3, 6 cm , HC = 6, 4 cm . Tính độ dài HA , AC và góc B , góc C .
b) Chứng minh: AM .AB = AN.AC và .
HB HC = AM .MB + AN.NC .
c) Qua A kẻ đường thẳng vuông góc với MN cắt BC tại K . Chứng minh rằng: K là
trung điểm của đoạn thẳng BC . Bài 6:
(0,5 điểm) Giải phương trình sau 4 1 5
+ x − = x + 2x − x x x HẾT
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1:
a) A = 3 8 − 2 18 + 20
A = 3.2 2 − 2.3 2 + 2 5 A = 6 2 − 6 2 + 2 5 A = 2 5 . 3 − 3 2 − 2 b) B = − 3 −1 1− 2 3 ( 3 − ) 1 2 ( 2 − ) 1 B = + 3 −1 2 −1 B = 3 + 2 Bài 2: a) 2x −1 = 4 Điề 1
u kiện: 2x −1 ≥ 0 ⇔ x ≥ . 2 2x −1 = 4 ⇔ 2x −1 =16 ⇔ 2x =16 +1 ⇔ 2x =17 17 ⇔ x = (thoả mãn) 2 17 Vậy x = . 2 b) 2
4x − 4x +1 = 3 −1 ⇔ ( x − )2 2 1 = 3 −1 ⇔ 2x −1 = 3 −1 3 − = − = 2 1 3 1 x x 2x = 3 ⇔ ⇔ ⇔ x − = − ( − ) 2 2 1 3 1
2x −1 = − 3 +1 − 3 + 2 x = 2 3 − 3 + 2 Vậy x ∈ ; 2 2 1 + 5 6 Bài 3:
a) Khi x = 1 (thoả mãn điều kiện) ta có Q = = = 3. 3 − 1 2
b) Với x ≥ 0 , x ≠ 9 ta có: x − 2 x +1 x − 4 x − 9 P = + + x − 3 x + 3 9 − x
( x −2)( x +3) ( x + )1( x −3) x−4 x −9 = ( + −
x − 3)( x + 3) ( x − 3)( x + 3) x − 9 x + x − 6 x − 2 x − 3 x − 4 x − 9 = ( + −
x − 3)( x + 3) ( x − 3)( x + 3) ( x − 3)( x + 3) x +
x − 6 + x − 2 x − 3 − x + 4 x + 9 = ( x −3)( x +3) x + 3 x
= ( x −3)( x +3) x ( x + 3) x = ( = . x − 3)( x + 3) x − 3 x Vậy P = . x − 3 x x + x 3 − x − x c) Ta có M = 5 P : Q = : = . = . x − 3 3 − x x − 3 x + 5 x + 5 − x Vì x ≥ 0 x
∀ ≥ 0 , x ≠ 9 ; x + 5 > 0 x
∀ ≥ 0 , x ≠ 9 nên M = ≤ 0 x ∀ ≥ 0 , x ≠ 9 x + 5 x ⇒ M = . x + 5 1 x 1 ⇒ M > ⇔ > 2 x + 5 2 x 1 ⇔ − > 0 x + 5 2 2 x − x − 5 ⇔ ( > x + ) 0 2 5
⇔ x − 5 > 0 (vì 2( x +5) > 0 x ∀ ≥ 0 , x ≠ 9 )
⇔ x > 5 ⇔ x > 25 (thỏa mãn). 1
Vậy x > 25 thì M > . 2 Bài 4: B 30° C 4,5 m A
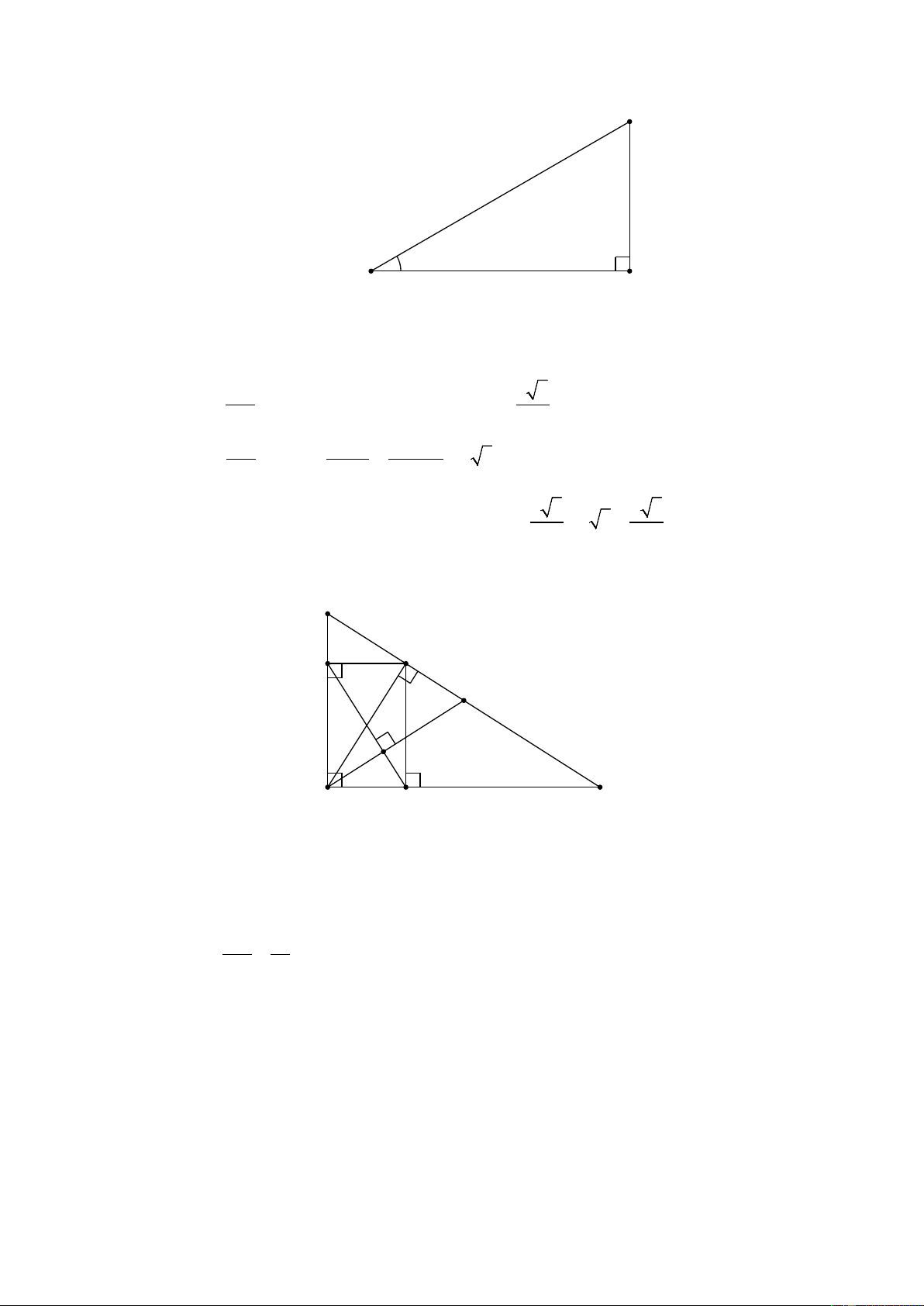
Gọi các điểm như trên hình vẽ, khi đó ta có chiều cao ban đầu của cây tre là AB + BC .
Trong tam giác vuông ABC có: AB 3 3 tan C =
⇒ AB = AC.tan C = 4,5.tan 30° = m . AC 2 AC AC 4, 5 cos C = ⇒ BC = = = 3 3m . BC cos C cos 30° 3 3 9 3
Vậy chiều cao ban đầu của cây tre là AB + BC = + 3 3 =
≈ 7,79m = 779cm . 2 2 Bài 5: B H M K E A C N
a) Xét tam giác ABC vuông tại A có: AH là đường cao 2 HA = .
HB HC = 3, 6.6, 4 ⇒ HA = 4,8 (cm). 2
AC = HC.BC = 6, 4.(3, 6 + 6, 4) ⇒ HC = 8 (cm) AC 8 sin B = = ⇒ B ≈ 53,13° . BC 10
C ≈ 90° − 53,13° ≈ 36,87° .
b) Xét tam giác AHB vuông tại H , HM là đường cao ⇒ 2
HA = AM .AB ( ) 1
Xét tam giác AHC vuông tại H , HN là đường cao ⇒ 2
HA = AN.AC (2) Từ ( )
1 và (2) suy ra AM .AB = AN.AC
Xét tứ giác ANHM có:
A = M = N = 90°
⇒ ANHM là hình chữ nhật. ⇒ MN = AH 2 ⇒ MN = . HB HC (3)
Xét tam giác AHB vuông tại H , HM là đường cao ta có: 2
HM = AM .BM
Xét tam giác AHC vuông tại H , HN là đường cao ta có: 2
HN = AN.CN
Xét tam giác MHN vuông tại H có: 2 2 2
MN = HM + HN = AM .MB + AN.NC (4) Từ (3) và (4) suy ra .
HB HC = AM .MB + AN.NC .
c) Theo câu a) ta có AM .AB = AM AN AN.AC ⇒ = . AC AB
Xét tam giác AMN và tam giác ACB có: AM AN = AMN = ACB AC AB ⇒ A ∆ BC ∽ A ∆ NM ⇒ = A chung ANM ABC Mà
KAC = AMN (cùng phụ với góc ANM ) ⇒ KAC = ACB ⇒ A
∆ KC cân tại K ⇒ KA = KC (5).
Chứng minh tương tự ta có ⇒ A
∆ KB cân tại K ⇒ KA = KB (6) .
Từ (5) và (6) suy ra KB = KC . 4 1 5 Bài 6: Cách 1:
+ x − = x + 2x − x x x x ≠ 0 Điề 1
u kiện: x − ≥ 0 x 5 2x − ≥ 0 x 4 1 5
+ x − = x + 2x − x x x 4 5 1
⇔ − x = 2x − − x − x x x 4 5 1 5 1 5 1 ⇔ − x .
2x − + x − = 2x − + x − . 2x − − x − x x x x x x x 4 5 1 5 1 ⇔ − x .
2x − + x − = 2x − − x + x x x x x 4 5 1 4 ⇔ − x .
2x − + x − = x − x x x x 4 5 1 4 ⇔ − x .
2x − + x − + − x = 0 x x x x 4 5 1 ⇔ − x .
2x − + x − +1 = 0 x x x 5 1 Mà 2x − + x − +1 > 0 x x 4 ⇔ − x = 0 x 2 ⇔ x = 4 ⇔ x = 2 ±
Thử lại điều kiện xác định x = 2 Vậy x = 2 4 1 5 Cách 2:
+ x − = x + 2x − ( )1 x x x Đặ 1 5 t a = x −
(a ≥ 0), b = 2x − (b ≥ 0) x x 1 5 4 Ta có: 2 2
a − b = x − − 2x + = − x x x x Do đó ( ) 1 2 2
⇔ a − b + a − b = 0 ⇔ (a − b).(a + b) + (a − b) = 0 ⇔ (a − b).(a + b + ) 1 = 0
a ≥ 0 , b ≥ 0 ⇒ a + b +1 > 0 ⇒ a − b = 0 ⇒ a = b 1 5
⇒ x − = 2x − 1 5 4
⇔ x − = 2x − ⇔ x − = 0 x x x x x x = 2 thoaû maõn 2 ( )
⇔ x − 4 = 0 ⇔ x = 2 − (loaïi)
Vậy phương trình có nghiệm x = 2 . HẾT




