Đề thi giữa kì môn Giải tích 1 năm 2014 | Đại học Bách Khoa Hà Nội

Đề thi giữa kì môn Giải tích 1 năm 2014 | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!

44 22 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Giải tích 1

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

24 trang 6 tháng trước

Tác giả:

Profile Thùy Dương
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 –Học kì 20141 1
Khóa 59 - Thời gian làm bài: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký
xác nhận số đề vào bài thi
Câu 1 (1 điểm). Tìm giới hạn lim
→



.
Câu 2 ( ).
1 điểm Khi , các VCB và → 0
(
)
= − ln(1 + )
() =
có tương đương không?
Câu 3 ( ). 1 điểm Điểm là điểm gián đoạn loại gì của hàm số sau = 0
=
1
arctan
2
+ 1
.
Câu 4 ( ). 1 điểm Tính đạo hàm cấp 100 của hàm số sau
=
(
+ 1
)
sin .
Câu 5 ( ).
1 điểm Sử dụng vi phân, tính gần đúng giá trị . =
.
Câu 6 ( ). 1 điểm Tìm cực trị của hàm số sau
=
2
+ 3
.
Câu 7 (2 điểm). Tính các tích phân sau
a)
∫

. b)
∫
( + 1) cos
.
Câu 8 ( ). 1 điểm Cho là hàm số khả vi tại 1 và biết rằng ()
lim
→
(
1 + 7
)
−
(
1 + 2
)
= 2.
Tìm .
(1)
Câu 9 ( ). 1 điểm Tìm sao cho , ∈
ĐỀ ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 – Học kì 20141 2
Khóa 59 - Thời gian làm bài: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký
xác nhận số đề vào bài thi
Câu 1 (1 điểm). Tìm giới hạn lim
→

()
.
Câu 2 ( ).
1 điểm Khi , các VCB và → 0
(
)
= − arctan
() =
có tương đương không?
Câu 3 ( ). 1 điểm Điểm là điểm gián đoạn loại gì của hàm số sau = 0
=
1
arcsin
3
+ 1
.
Câu 4 ( ). 1 điểm Tính đạo hàm cấp 100 của hàm số sau
=
(
+ 1
)
cos .
Câu 5 ( ).
1 điểm Sử dụng vi phân, tính gần đúng giá trị . =
.
Câu 6 ( ). 1 điểm Tìm cực trị của hàm số sau
=
3
+ 2
.
Câu 7 (2 điểm). Tính các tích phân sau
a)
∫

. b)
∫
( + 2) sin
.
Câu 8 ( ). 1 điểm Cho là hàm số khả vi tại 1 và biết rằng ()
lim
→
(
1 + 5
)
− (1 + 3)
= 1.
Tìm .
(1)
Câu 9 ( ). 1 điểm Tìm sao cho , ∈
lim
→

− 1 +  +
= 0.
lim
→
ln(1 + 3) +  +
= 0.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 –Học kì 20141 3
Khóa 59 - Thời gian làm bài: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký
xác nhận số đề vào bài thi
Câu 1 (2 điểm). Tìm các giới hạn sau
a) lim
→


. b) lim
→
(
1 + 2
)

.
Câu 2 ( ). 1 điểm Tìm và phân loại điểm gián đoạn của hàm số sau
=
arctan
+
.
Câu 3 ( ).
1 điểm Cho hàm số
(
)
=

. Tính

(0).
Câu 4 ( ). 1 điểm Sử dụng vi phân, tính gần đúng giá trị =
√
1.02
.
Câu 5 ( ). 1 điểm Tìm cực trị của hàm số sau
=
+ 3
2
.
Câu 6 (2 điểm). Tính các tích phân sau
a)
∫
(
+ 1
)

. b)
∫


.
Câu 7 ( ). 1 điểm Cho
lim
→
(
)
− 5
− 1
= 2.
Tìm lim
→
().
Câu 8 ( ). 1 điểm Tìm các tiệm cận của hàm số sau
=
sin
2
.
ĐỀ ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 – Học kì 20141 4
Khóa 59 - Thời gian làm bài: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký
xác nhận số đề vào bài thi
Câu 1 (2 điểm). Tìm các giới hạn sau
a) lim
→


. b) lim
→
(
1 − 3
)

.
Câu 2 ( ). 1 điểm Tìm và phân loại điểm gián đoạn của hàm số sau
=
sin
−
.
Câu 3 ( ).
1 điểm Cho hàm số
(
)
=

. Tính

(0).
Câu 4 ( ). 1 điểm Sử dụng vi phân, tính gần đúng giá trị =
√
1.01
.
Câu 5 ( ). 1 điểm Tìm cực trị của hàm số sau
=
+ 2
3
.
Câu 6 (2 điểm). Tính các tích phân sau
a)
∫
(
+ 3
)

. b)
∫


.
Câu 7 ( ). 1 điểm Cho
lim
→
(
)
+ 3
− 2
= 1.
Tìm lim
→
().
Câu 8 ( ). 1 điểm Tìm các tiệm cận của hàm số sau
=
sin
1
.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
VIÞN TOÁN þNG DþNG VÀ TIN HÞC VIÞN TOÁN þNG DþNG VÀ TIN HÞC
Þ 5 Þ THI GIþA Kþ MÔN GI¾I TÍCH 1 3 Hßc kì 20141
Khóa: K59 Thßi gian: 60 phút
Chú ý: Thí sinh không ±ÿc sÿ dÿng tài lißu và giám thß ph¿i ký
xác nh¿n sß ß vào bài thi
Câu 1. Tìm t¿p xác ßnh cÿa hàm sß
(
)
arcsin 2 1
y x
= +
.
Câu 2. Tìm
m
ß hàm sß
2
1 cos2
khi 0,
( )
khi 0
x
x
f x
x
m x
2ù
b
ü
=
ú
ü
û
liên tÿc t¿i
0
x
=
.
Câu 3. Khi
0
x
+
³ c¿p vô cùng bé sau có t±¡ng ±¡ng không?
3 2
( )
x x x
³
= +
và
sin
( ) cos2
x
x e x
´
= 2 .
Câu 4. Tìm cÿc trß cÿa hàm sß
( ) ln( 2)
f x x x
= + 2
.
Câu 5. Tính tích phân
( 1)
( 2)( 3)
x dx
x x
+
+ +
+
.
Câu 6. Tính
'(3)
f vßi
(2 )(3 ) khi 3,
( )
3 khi 3.
x x x
f x
x x
2 2 f
ù
=
ú
2 >
û
Câu 7. Tính gißi h¿n
3
2 1
lim
3 ln( 2)
x
x
x x
³
û þ
2
2
ü ÿ
2 2
ý ø
.
Câu 8. Tính tích phân arcsin
xdx
+
.
Câu 9. Cho hàm sß
( )
f x
liên tÿc trên
[1, )
+>
và kh¿ vi trên
(1, )
+>
thßa mãn
lim ( ) (1)
x
f x f
³+>
=
. Chÿng minh r¿ng tßn t¿i
1
c
>
sao cho
'( ) 0
f c
=
.
Câu 10. Tìm t¿t c¿ hàm sß
( )
f x
kh¿ vi trên
=
thßa mãn
( ) ( ) sin( ) , , .
f a f b a b a b a b
2 f 2 2 " *
=
Thang ißm: Mßi câu 1 ißm.
Þ 6 Þ THI GIþA Kþ MÔN GI¾I TÍCH 13 Hßc kì 20141
Khóa: K59 Thßi gian: 60 phút
Chú ý: Thí sinh không ±ÿc sÿ dÿng tài lißu và giám thß ph¿i ký
xác nh¿n sß ß vào bài thi
Câu 1. Tìm t¿p xác ßnh cÿa hàm sß
(
)
arccos 1 2
y x
= 2 .
Câu 2. Tìm
m
ß hàm sß
2
1 cos4
khi 0,
( )
khi 0
x
x
f x
x
m x
2ù
b
ü
=
ú
ü
û
liên tÿc t¿i
0
x
=
.
Câu 3. Khi
0
x
³
c¿p vô cùng bé sau có t±¡ng ±¡ng không?
4 3
3
( )
x x x
³
= +
và
tan
( ) cos4
x
x e x
´
= 2 .
Câu 4. Tìm cÿc trß cÿa hàm sß
( ) ln( 3)
f x x x
= 2 +
.
Câu 5. Tính tích phân
( 2)
( 3)( 4)
x dx
x x
+
+ +
+
.
Câu 6. Tính
'(4)
f vßi
(3 )( 4) khi 4,
( )
4 khi 4.
x x x
f x
x x
2 2 f
ù
=
ú
2 >
û
Câu 7. Tính gißi h¿n
2
1 1
lim
2 ln( 1)
x
x
x x
³
û þ
2
2
ü ÿ
2 2
ý ø
.
Câu 8. Tính tích phân arccos
xdx
+
.
Câu 9. Cho hàm sß
( )
f x
liên tÿc trên
( ,1]
2>
và kh¿ vi trên
( ,1)
2 >
thßa mãn
lim ( ) (1)
x
f x f
³2>
=
. Chÿng minh r¿ng tßn t¿i
1
c
<
sao cho
'( ) 0
f c
=
.
Câu 10. Tìm t¿t c¿ hàm sß
( )
f x
kh¿ vi trên
=
thßa mãn
( )
( ) ( ) | || 1|, , .
a b
f a f b a b e a b
2
2 f 2 2 " *
=
Thang ißm: Mßi câu 1 ißm.
H¾T
H¾T
H¾T
CuuDuongThanCong.com https://fb.com/tailieudientucntt
VIÞN TOÁN þNG DþNG VÀ TIN HÞC VIÞN TOÁN þNG DþNG VÀ TIN HÞC
Þ 7 Þ THI GIþA Kþ MÔN GI¾I TÍCH 1 3 Hßc kì 20141
Khóa: K59 Thßi gian: 60 phút
Chú ý: Thí sinh không ±ÿc sÿ dÿng tài lißu và giám thß ph¿i ký
xác nh¿n sß ß vào bài thi
Câu 1. Tìm hàm sß ng±ÿc cÿa hàm sß
2 3
4 5
x
y
x
+
=
+
.
Câu 2. Phân lo¿i ißm gián o¿n
2
x
Ã
=
cÿa hàm sß
tan
1
( )
1 4
x
f x =
+
.
Câu 3. Cho hàm sß
3
( )
x
f x xe
=
. Tính ¿o hàm c¿p cao
(5)
( )
f x
.
Câu 4.
Chÿng minh r¿ng
2
2 arctan ln(1 ), 0.
x x x x
g + " g
Câu 5. Tính gißi h¿n
cot
0
lim(cos )
x
x
x
³
.
Câu 6. Tính tích phân
arctan(2 )
x dx
+
.
Câu 7. Tính gißi h¿n
2
0
sin
lim
x
x
e x x
x
³
2
.
Câu 8. Tính tích phân
2 2
( 2) ( 3)
dx
x x+ +
+
.
Câu 9. Tính ¿o hàm c¿p cao
(19)
(0)
y vßi
arcsin
y x
=
.
Câu 10. Cho hàm sß : (0, )f
+> ³
=
thßa mãn
( ) 1
f x
f
và
''( ) 0
f x
g
vßi mßi
0
x
>
. Chÿng minh r¿ng
'( ) 0
f x
f
vßi mßi
0
x
>
.
Thang ißm: Mßi câu 1 ißm.
H¾T
Þ 8 Þ THI GIþA Kþ MÔN GI¾I TÍCH 13 Hßc kì 20141
Khóa: K59 Thßi gian: 60 phút
Chú ý: Thí sinh không ±ÿc sÿ dÿng tài lißu và giám thß ph¿i ký
xác nh¿n sß ß vào bài thi
Câu 1. Tìm hàm sß ng±ÿc cÿa hàm sß
3 4
5 6
x
y
x
+
=
+
.
Câu 2. Phân lo¿i ißm gián o¿n
0
x
=
cÿa hàm sß
cot
1
( )
1 5
x
f x =
+
.
Câu 3. Cho hàm sß
2
( )
x
f x xe
= . Tính ¿o hàm c¿p cao
(6)
( )
f x
.
Câu 4. Chÿng minh r¿ng
ln( 1) , 0.
x x x
+ f " g
Câu 5. Tính gißi h¿n
tan
2
lim(sin )
x
x
x
Ã
³
.
Câu 6. Tính tích phân
arctan(3 )
x dx
+
.
Câu 7. Tính gißi h¿n
3
0
cos 1
lim
x
x
e x x
x
³
2 2
.
Câu 8 . Tính tích phân
2 2
( 3) ( 4)
dx
x x+ +
+
.
Câu 9. Tính ¿o hàm c¿p cao
(17)
(0)
y vßi
arccos
y x
=
.
Câu 10. Cho hàm sß : ( ,0)f
2> ³
=
thßa mãn
( ) 1
f x
f
và
''( ) 0
f x
g
vßi mßi
0
x
<
. Chÿng minh r¿ng
'( ) 0
f x
g
vßi mßi
0
x
<
.
Thang ißm: Mßi câu 1 ißm.
H¾T
CuuDuongThanCong.com https://fb.com/tailieudientucntt
ĐÁP ÁN ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 – ĐỀ 1
Câu 1.
lim
→



=
(0.5đ+0.5đ)
Câu 2.
L’Hospital lim
→
()
= lim
→


(0.5đ)
= lim
→

= 1. Hai VCB tương đương (0.5đ)
Câu 3. lim
→
arctan


= lim
→
×


= 2. (0.5đ) Điểm là điểm gián đoạn bỏ được. (0.5đ) = 0
Câu 4.
Áp dụng CT Leibnitz (0.5đ)
()
=
(
+ 1
)(
sin
)
()
+ 100 sin
(
+ 1
)
′
( )
()
()
=
(
+ 1
)
sin( + 50) + 100sin( +

) =
(
+ 1
)
sin − 100cos. (0.5đ)
Câu 5.
Xét ,
(
)
=
(
)
=
. (0.5đ) Ta có =
(
0.01 +
)
≈
(
0
)
(
0
)
× 0.01 =1.01 (0.5đ)
Câu 6.
TXĐ: R. Đạo hàm
=

( )
.
= 0: = −
√
3, =
√
3. (0.5đ)
= −
√
3 là điểm cực tiểu

= −
√
3 = −
√
. là điểm cực đại =
√
3
Đ
= 
√
3 =
√
. (0.5đ)
Câu 7.
a)
∫

 =
∫


 =
∫
(
+ + 1 +

) (0.5đ)
=
+
+ + ln| − 1| + . (0.5đ)
b)
∫
(
+ 1
)
(1 + cos2) =
∫
(
+ 1
)
 +
∫
(
+ 1
)
(
sin2
)
(0.5đ)
=
+
+
(
+ 1
)
sin2 −
∫ sin2  =
+
+
(
+ 1
)
sin2 +
cos2 + . (0.5đ)
Câu 8.
khả vi tại 1, nên
(
1
)
= lim
→
( )
 ()
. (0.5đ)
Ta có
2 = lim
→
( )
 ()
= lim
→
7
( ) ( )
 

− 2
( ) ( )
 

= 7
(
1
)
− 2
(
1
)
=
5 (1)
. Suy ra
(
1
)
=
. (0.5đ)
Câu 8.
Ta có 0 = lim
→
( ×


) = lim
→
(


+ + ) = 2 + . (0.5đ)
Suy ra .
= −2 = − lim
→


= −lim
→




= −2. (0.5đ)
Cách 2 Dùng khai triển hữu hạn.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
ĐÁP ÁN ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 – ĐỀ 2
Câu 1.
lim
→

()
=
(0.5đ+0.5đ)
Câu 2.
L’Hospital lim
→

= lim
→


(0.5đ)
= lim
→

= 1. Hai VCB tương đương (0.5đ)
Câu 3. lim
→
arctan


= lim
→
×


= 3. (0.5đ) Điểm là điểm gián đoạn bỏ được. (0.5đ) = 0
Câu 4.
Áp dụng CT Leibnitz
()
=
(
+ 1
)(
cos
)
()
+ 100 + 1 cos
( )
′
( )
()
(0.5đ)
()
=
(
+ 1
)
cos( + 50) + 100cos( +

) =
(
+ 1 cos + 100sin.
)
(0.5đ)
Câu 5.
Xét , . (0.5đ) Ta có
(
)
=
′
(
)
=
=
(
0.02 +
)
≈
(
0
)
(
0
)
× 0.02 =1.02 (0.5đ)
Câu 6.
TXĐ: R. Đạo hàm
=

( )
.
= 0: = −
√
2, =
√
2. (0.5đ)
= −
√
2 là điểm cực tiểu

= −
√
2 = −
√
. là điểm cực đại =
√
2
Đ
= 
√
2 =
√
. (0.5đ)
Câu 7.
a)
∫

 =
∫


 =
∫
(
− + 1 −

) (0.5đ)
=
−
+ − ln| + 1| + . (0.5đ)
b)
∫
(
+ 2
)
(1 − cos2) =
∫
(
+ 2
)
 −
∫
(
+ 2
)
(
sin2
)
(0.5đ)
=
+ −
(
+ 2
)
sin2 +
∫ sin2 =
+ −
(
+ 2
)
sin2 −
cos2 + . (0.5đ)
Câu 8.
khả vi tại 1, nên
(
1
)
= lim
→
( )
 ()
. (0.5đ)
Ta có
1 = lim
→
( )
 ()
= lim
→
5
( ) ( )
 

− 3
( ) ( )
 

= 5
(
1
)
− 3
(
1
)
=
2 (1)
. Suy ra
(
1
)
=
. (0.5đ)
Câu 8.
Ta có 0 = lim
→
( ×
()
) = lim
→
(
()
+ + ) = 3 + . (0.5đ)
Suy ra .
= −3 = − lim
→
()
= −lim
→



=
. (0.5đ)
Cách 2 Dùng khai triển hữu hạn.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
ĐÁP ÁN ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 – ĐỀ 3
Câu 1. a) lim
→


= lim
→

= 1 (0.5đ+0.5đ)
b) lim
→
(
1 + 2
)

=

→
 ()
(0.5đ) =

→
()

=
. (0.5đ)
Câu 2. Hàm số có 2 điểm gián đoạn và = 0 = −1
lim
→


= lim
→

= 1. Điểm là điểm gián đoạn bỏ được. (0.5đ) = 0
lim
→


= ∞. Điểm là điểm gián đoạn loại hai. (0.5đ) = −1
Câu 3.
Hàm
(
)
=

=
+ + 1 +

. Đạo hàm
()
(
)
=

()
=
!
(

)

. (0.5đ)

(
0
)
= = −10!
(

)
(
0
)( )


(

)

. (0.5đ)
Câu 4.
Xét hàm số
(
)
=
√
. Ta có (0.5đ)
=
(
1.02 +
)
≈
(
1
)
(
1
)
× 0.02 = 1 +
.
≈1.006667. (0.5đ)
Câu 5.
TXĐ: . Đạo hàm ≠ 0
=


.
= 0: = −
√
3, =
√
3. (0.5đ)
= −
√
3 là điểm cực đại
Đ
= −
√
3 = −
√
3. là điểm cực tiểu =
√
3

= 
√
3 =
√
3. (0.5đ)
Câu 6.
a)
∫
(
+ 1
)

 =
∫
(
+ 1
)
(

)
(0.5đ)
=
(
+ 1
)

−
∫

 =
(
+ 1
)

−

+ . (0.5đ)
b)
∫


 =
∫
(
−

) (0.5đ) = 2ln|| −
ln|
+ 1| + . (0.5đ)
Câu 7.
Ta có lim (
→
(
)
− 5) = lim
→
( − 1)
( )


= 0 × 2 = 0.(0.5đ) Suy ra lim
→
(
)
= 5.
(0.5đ)
Câu 8. lim
→
= 0: hàm số không có tiệm cận đứng.
lim sin
→
= lim
→
×
= ∞. lim
→
= lim
→
 sin
= 2, đặt =
(0.5đ)
lim
→
(
− 2
)
= lim
→
sin
2
− 2
= lim
→
1
sin2
− 2
= lim
→
sin2 − 2
= 0.
Tiệm cận xiên . (0.5đ) = 2
CuuDuongThanCong.com https://fb.com/tailieudientucntt
ĐÁP ÁN ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 – ĐỀ 4
Câu 1. a) lim
→


= lim
→


=
(0.5đ+0.5đ)
b) lim
→
(
1 − 3
)

=

→
 ()
(0.5đ) =

→
()

=

(0.5đ)
Câu 2. Hàm số có 2 điểm gián đoạn và = 0 = 1
lim
→


= lim
→


= −1. Điểm là điểm gián đoạn bỏ được. (0.5đ) = 0
lim
→


= ∞ = 1. Điểm là điểm gián đoạn loại hai. (0.5đ)
Câu 3.
Hàm
(
)
=

=
− + 1 −

. Đạo hàm
()
(
)
= −

()
=
!
(

)

. (0.5đ)

(
0
)
= = −10!
(

)
(
0
)( )


(

)

. (0.5đ)
Câu 4.
Xét hàm số
(
)
=
√
. Ta có (0.5đ)
=
(
1.01 +
)
≈
(
1
)
(
1
)
× 0.01 = 1 +
.
= 1.0025. (0.5đ)
Câu 5.
TXĐ: . Đạo hàm ≠ 0
=


.
= 0: = −
√
2, =
√
2. (0.5đ)
= −
√
2 là điểm cực đại
Đ
= −
√
2 = −
√
. là điểm cực tiểu =
√
2

= 
√
2 =
√
.(0.5đ)
Câu 6.
a)
∫
(
+ 3
)

 =
∫
(
+ 3
)
(

)
(0.5đ)
=
(
+ 3
)

−
∫

 =
(
+ 3
)

−

+ . (0.5đ)
b)
∫

)
∫

 =
∫
(

+
( )
) (0.5đ) =
ln|| +
ln(
+ 2) + . (0.5đ)
Câu 7.
Ta có lim (
→
(
)
+ 3) = lim
→
( − 2)
( )


= 0 × 1 = 0. (0.5đ) Suy ra lim
→
(
)
= −3.
(0.5đ)
Câu 8. lim
→
= 0: hàm số không có tiệm cận đứng.
lim sin
→
= lim
→
×
= ∞. lim
→
= lim
→
 sin
= 1, đặt =
(0.5đ)
lim
→
(
−
)
= lim
→
sin
1
− 1 = lim
→
1
sin
− 1 = lim
→
sin −
= 0.
Tiệm cận xiên . (0.5đ) =
CuuDuongThanCong.com https://fb.com/tailieudientucntt
ÁP ÁN Þ 5
Câu 1. +) ißu kißn xác ßnh:
1 2x 1 1
2 f + f
, +)
1 x 0
õ 2 f f
. T¿p xác ßnh
[ 1,0]
= 2
.
Câu 2. +)
2
0 0
1 cos2x
lim ( ) lim 2
³ ³
2
= =
. +) Hàm sß liên tÿc t¿i
0
=
0
(0) lim ( ) 2
³
õ = = =
.
Câu 3. Khi
0
+
³ :
3 2
) ( ) ~
³
+ = +
, +)
sinx
( ) ( 1) (1 cos2x)
´
= 2 + 2
,
sinx
1 ~ sinx ~
2 ,
2
1 cos2x ~ 2x
2
( ) ~
´
ó
. V¿y
( ) ~ ( )
³ ´
.
Câu 4. +)
1 1
2, '( ) 1 0
2 2
2 2
> 2 = 2 = =
+ +
1
õ = 2
.
+) Xét d¿u
'( )
ta có
( )
¿t cÿc ¿i
1
t¿i
1.
= 2
Câu 5. +)
( 1) x 1 2
x
( 2)( 3) 2 3
+ 2
þ ù
= = +
ÿ ú
+ + + +
ø û
+ +
,+)
ln | 2 | 2ln | 3 |
= 2 + + + +
.
Câu 6. +)
'
3
3
(3) lim 1.
3
+
+
³
2
= =
2
+)
'
3
(2 )(3 )
(3) lim 1.
3
2
2
³
2 2
= =
2
KL:
' ' '
(3) (3) (3) 1.
+ 2
= = =
Câu 7. +)
3 3
2
( 2)ln( 2) 3 ( 2)ln( 2) 3
lim lim ,
( 3)ln[1 ( 3)] ( 3)
³ ³
2 2 2 + 2 2 2 +
= =
2 + 2 2
+)
'
3
ln( 2) 1
lim
2( 3) 2
³
2
= =
2
Câu 8. +)
2
arcsin arcsin
1


= 2
2
+ +
,+)
2
arcsin 1 .
= + 2 +
Câu 9. +) Xét
1
( ) , (0,1]
û þ
= *
ü ÿ
ý ø
,
0
(0) : lim ( ) lim ( ) (1) (0) (1)
+
³+>
³
= = = ó =
.
+)
( )
thßa mãn ßnh lí Rolle trên
[0,1]
nên
0 0
(0,1) | '( ) 0,
# * =
¿t
0
1
=
ta có
'( ) 0
=
.
Câu10.+)
0
" *
=
,
0 0 0 0
( ) ( ) sin( ) ,
2 f 2 2 " b
0
0
0
0 0 0
0 0
( ) ( )
( ) ( )
sin( ) , '( ) lim 0
³
2
2
ó f 2 " b ó = =
2 2
.
+ )
' 0 ons
c ó =
(thßa mãn).
Thang ißm: mßi d¿u +) là 0,5 ißm
CuuDuongThanCong.com https://fb.com/tailieudientucntt
ÁP ÁN Þ 6
Câu 1. +) ißu kißn xác ßnh:
1 1 2x 1
2 f 2 f
, +)
0 x 1
õ f f
. T¿p xác ßnh
[0,1]
=
.
Câu 2. +)
2
0 0
1 cos4x
lim ( ) lim 8
³ ³
2
= =
. +) Hàm sß liên tÿc t¿i
0
=
0
(0) lim ( ) 8
³
õ = = =
.
Câu 3. Khi
0
³
:
4 33
) ( ) ~
³
+ = +
, +)
tanx
( ) ( 1) (1 cos4x)
´
= 2 + 2
,
tanx
1 ~ tan x ~
2 ,
2
1 cos4x ~ 8x
2
( ) ~
´
ó
. V¿y
( ) ~ ( )
³ ´
.
Câu 4.+)
1 2
3, '( ) 1 0 2
3 3
+
> 2 = 2 = = õ = 2
+ +
.
+) Xét d¿u
ta có
( )
¿t cÿc tißu
2
2
t¿i
2.
= 2
Câu 5. +)
( 2) x 1 2
x
( 3)( 4) 3 4
+ 2
þ ù
= = +
ÿ ú
+ + + +
ø û
+ +
,+)
ln | 3| 2ln | 4 |
= 2 + + + +
.
Câu 6. +)
'
4
4
(4) lim 1.
4
+
+
³
2
= = 2
2
+)
'
4
(3 )( 4)
(4) lim 1.
4
2
2
³
2 2
= = 2
2
KL:
' ' '
(4) (4) (4) 1.
+ 2
= = = 2
Câu 7. +)
2 2
2
( 1)ln( 1) 2 ( 1)ln( 1) 2
lim lim ,
( 2) ln[1 ( 2)] ( 2)
³ ³
2 2 2 + 2 2 2 +
= =
2 + 2 2
+)
'
2
ln( 1) 1
lim
2( 2) 2
³
2
= =
2
Câu 8. +)
2
arccos arccos
1


= +
2
+ +
,+)
2
arccos 1
= 2 2 +
.
Câu 9. +) Xét
1
( ) 2 , [ 1,0)
û þ
= + * 2
ü ÿ
ý ø
,
0
(0) : lim ( ) lim ( ) (1) (0) ( 1)
2
³2>
³
= = = ó = 2
.
+)
( )
thßa mãn ßnh lí Rolle trên
[ 1,0]
2
nên
0 0
( 1,0) | '( ) 0,
# * 2 =
ta có
0
1
'( 2) 0
+ =
.
Câu10.+)
0
" *
=
,
0
0 0 0
( ) ( ) 1 ,
2
2 f 2 2 " b
0
0
0
0
0 0
0 0
( ) ( )
( ) ( )
1 , '( ) lim 0
2
³
2
2
ó f 2 " b ó = =
2 2
.
+ )
' 0 ons
c ó =
(thßa mãn).
Thang ißm: mßi d¿u +) là 0,5 ißm
CuuDuongThanCong.com https://fb.com/tailieudientucntt
ÁP ÁN Þ 7
Câu 1. +)
5 2x 3 3 5 1
, ,
4 4x 5 4 2 2
+ 2
û þ
b 2 = õ = b
ü ÿ
+ 2
ý ø
.+) Hàm sß ng±ÿc c¿n tìm:
3 5 1
,
4 2 2
2
û þ
= b
ü ÿ
2
ý ø
.
Câu 2.
2 2
) lim ( ) 0, lim ( ) 1.
à Ã
2 +
³ ³
+ = =
+)
2 2
lim ( ) lim ( )
2
à Ã
Ã
+ 2
³ ³
b ó =
là ißm gián o¿n lo¿i 1.
Câu 3. +)
(
)
(5)
3x 3x (5) 1 3x (4)
5
( ) ( )'( )
 = + , +)
5 3x 4 3x
3 5.3

= + .
Câu 4.
+) Xét hàm sß
2
( ) 2 arctan ln(1 ), 0
= 2 + g
,
'( ) 2arctan 0, 0.
= > " >
+)
( )
ó
ßng bi¿n khi
0
g
( ) (0) 0, 0.
ó g = " g
Câu 5. +)
0
lim cot ln cos
cot cot ln cos
0 0
lim(cos ) lim .
³
³ ³
= = =
+)
'
2
ln cos tan
lim cot lncos lim lim 0, 1.
1
t anx
0 0 0
cos
2
= = = ó =
³ ³ ³
Câu 6. +)
2
2
2xdx 1
arctan(2 ) arctan(2 ) , ) arctan(2 ) ln(1 4x ) .
1 4x 4

= = 2 + = 2 + +
+
+ +
.
Câu 7. +)
' '
2
0 0 0
sin sin cos 1 2 cos
lim lim , ) lim 1.
2 2
³ ³ ³
2 + 2
= + = =
Câu 8. +)
2 2
x 1 2 1 2 1 1
+ , ) 2ln|x+2| +2ln|x+3|+C.
( 2) ( 3) (x+2)² x+2 (x+3)² x+3 2 3

û þ
= + + =
ü ÿ
+ + + +
ý ø
+ +
Câu 9. +)
2 2 2 2
2 2
1
' (1 ) ' 1 (1 ) '' 2 ' ' (1 ) '' ' 0.
1 1
  
2
= ó 2 = 2 ó 2 2 = = 2 ó 2 2 =
2 2
+)
(
)
( )
2 2 ( 2) ( 1) ( 1)
(1 ) '' ' 0 (1 ) .2x. ( 1) . 0
 
+ + +
ó 2 2 = ó 2 2 2 2 2 2 =
,
( ) ( )
2 2
( 2) 2 ( ) (19) 2 (17)
(0) (0) (0) 17 (0) 17!! '(0) 17!! .
+
ó = ó = = = =ï
Câu 10.
+) Ph¿n chÿng, gi¿ sÿ có
0
0
>
sao cho
0
'( ) 0
>
. Do
''( ) 0
g
nên
0 0
'( ) '( ),
g " >
.
+) Theo Lagrange:
0 0 0 0 0 0
( , ) | ( ) ( ) '( )( ) ( ) '( )( ) 1
³+>
# * = + 2 g + 2 ³ + > >
(trái gt).
Thang ißm: mßi d¿u +) là 0,5 ißm
CuuDuongThanCong.com https://fb.com/tailieudientucntt
ÁP ÁN Þ 8
Câu 1. +)
6 3x 4 4 6 3
, ,
5 5x 6 5 3 5
+ 2
û þ
b 2 = õ = b
ü ÿ
+ 2
ý ø
.+) Hàm sß ng±ÿc c¿n tìm:
4 6 3
,
5 3 5
2
û þ
= b
ü ÿ
2
ý ø
.
Câu 2.
0 0
) lim ( ) 0, lim ( ) 1.
+ 2
³ ³
+ = =
+)
0 0
lim ( ) lim ( ) 0
+ 2
³ ³
b ó =
là ißm gián o¿n lo¿i 1.
Câu 3. +)
(
)
(6 )
2x 2x (6) 1 2x (5)
6
( ) ( )'( )
 = + , +)
6 2x 5 2x
2 6.2

= + .
Câu 4. +) Xét hàm sß
ln( 1), 0.
2 + g
1
'( ) 1 0.
1 1
= 2 = g
+ +
+)
( )
ó
ßng bi¿n,
( ) (0) 0, 0
g = " g
.
Câu 5. +)
tan
2
lim(sin )
Ã
³
=
2
lim tan lnsin
tan lnsin
2
lim .
Ã
Ã
³
³
= =
+)
'
2
lnsin cot
lim tan lnsin lim lim 0, 1.
1
cotx
sin
2 2 2
à à Ã
= = = ó =
2
³ ³ ³
Câu 6. +)
2
2
3xdx 1
arctan(3 ) arctan(3 ) , ) arctan(3 ) ln(1 9x ) .
1 9x 6

= = 2 + = 2 + +
+
+ +
Câu 7. +)
' '
3 2
0 0 0
cos 1 1
lim lim , ) l
co
i
s sin 1 2
m
s
3 6
i
3
n
³ ³ ³
2 2 2
= + =
= 2
2 2
.
Câu 8. +)
2 2
x 1 2 1 2 1 1
+ , ) 2ln|x+3| +2ln|x+4|+C.
( 3) ( 4) (x+3)² x+3 (x+4)² x+4 3 4

û þ
= + + =
ü ÿ
+ + + +
ý ø
+ +
Câu 9. +)
2 2 2 2
2 2
1
' (1 ) ' 1 (1 ) '' 2 ' ' (1 ) '' ' 0.
1 1

2
= ó 2 = 2 2 ó 2 2 = = 2 ó 2 2 =
2 2
+)
(
)
( )
2 2 ( 2) ( 1) ( 1)
(1 ) '' ' 0 (1 ) .2x. ( 1) . 0
 
+ + +
ó 2 2 = ó 2 2 2 2 2 2 =
,
( ) ( )
2 2
( 2) 2 ( ) (17) 2 (15)
(0) (0) (0) 15 (0) 15!! '(0) 15!! .
+
ó = ó = = = = 2ï
Câu 10.
+) Ph¿n chÿng, gi¿ sÿ có
0
0
sao cho
0
'( ) 0
. Do
''( ) 0
nên
0 0
'( ) '( ),
.
+) Theo Lagrange:
0 0 0 0 0 0
( , ) | ( ) ( ) '( )( ) ( ) '( )( ) 1
³2>
# * = + 2 g + 2 ³ + > >
(trái gt).
Thang ißm: mßi d¿u +) là 0,5 ißm
CuuDuongThanCong.com https://fb.com/tailieudientucntt
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

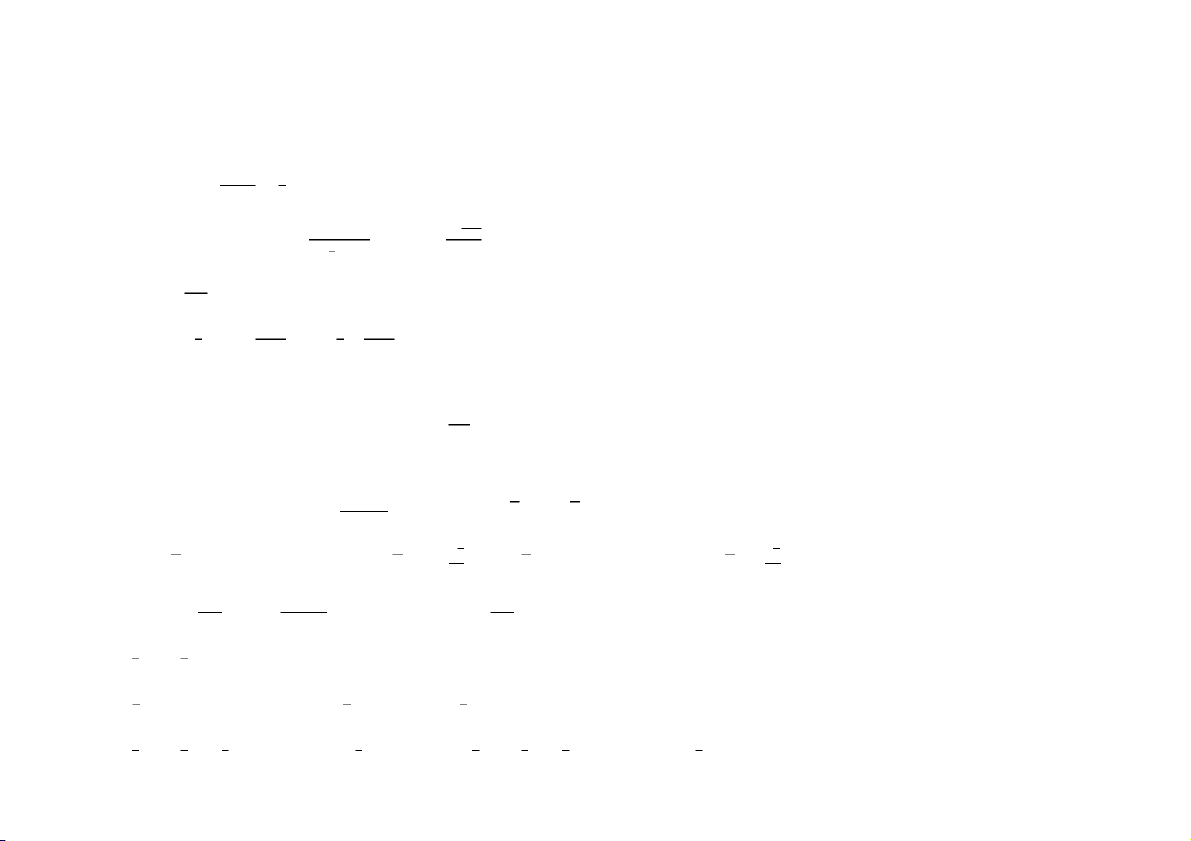
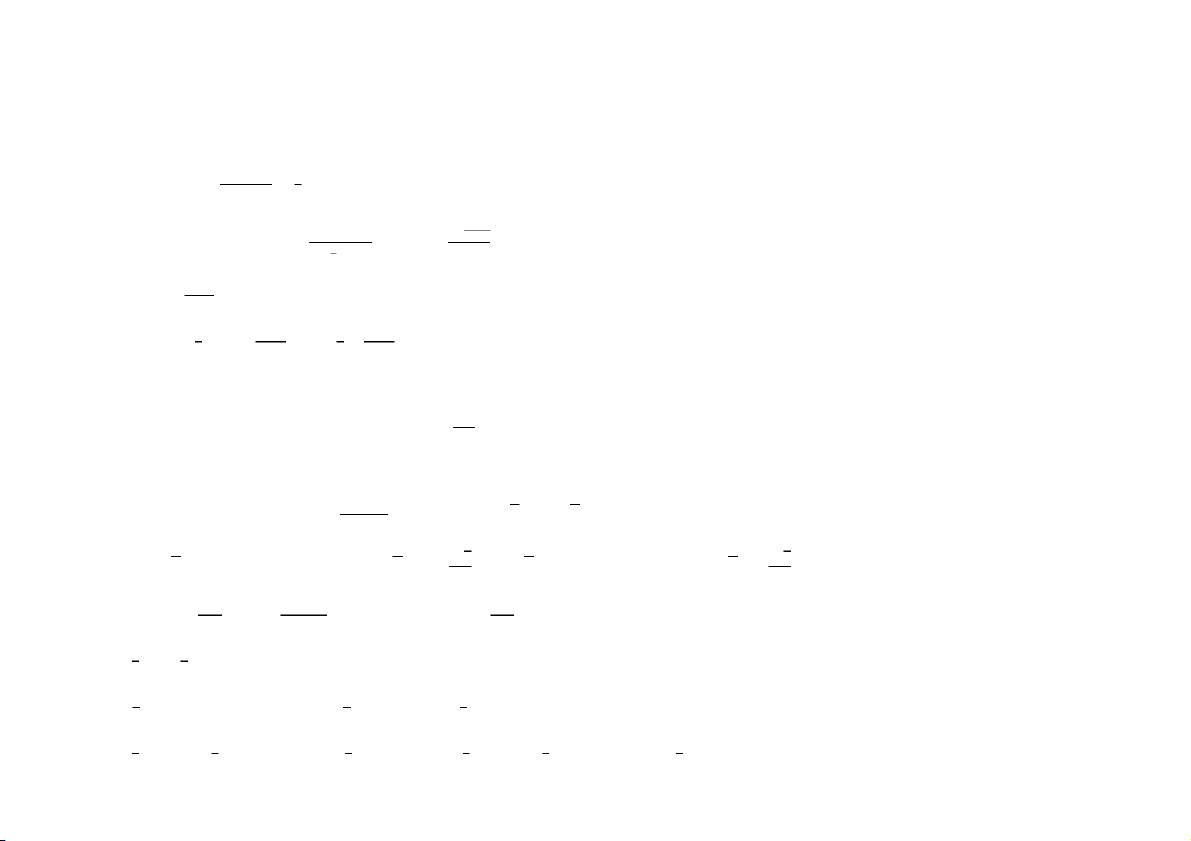
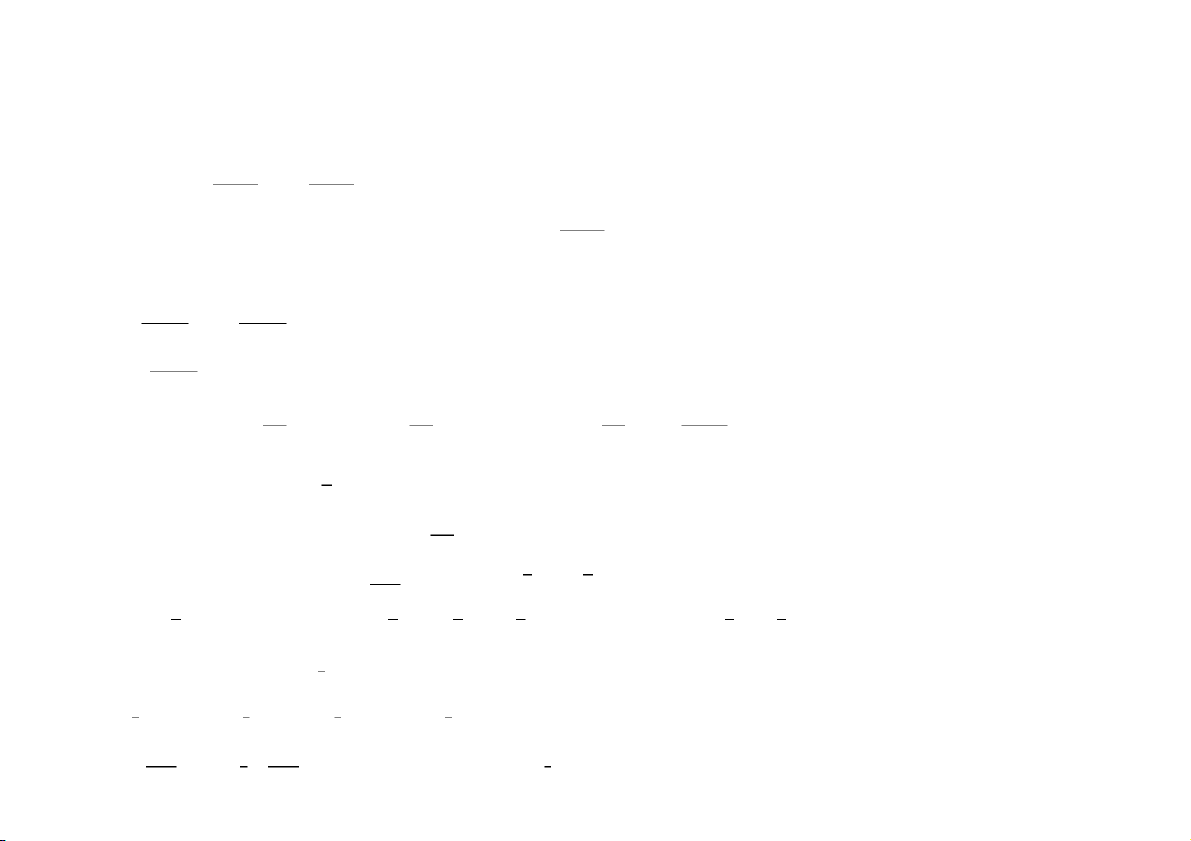
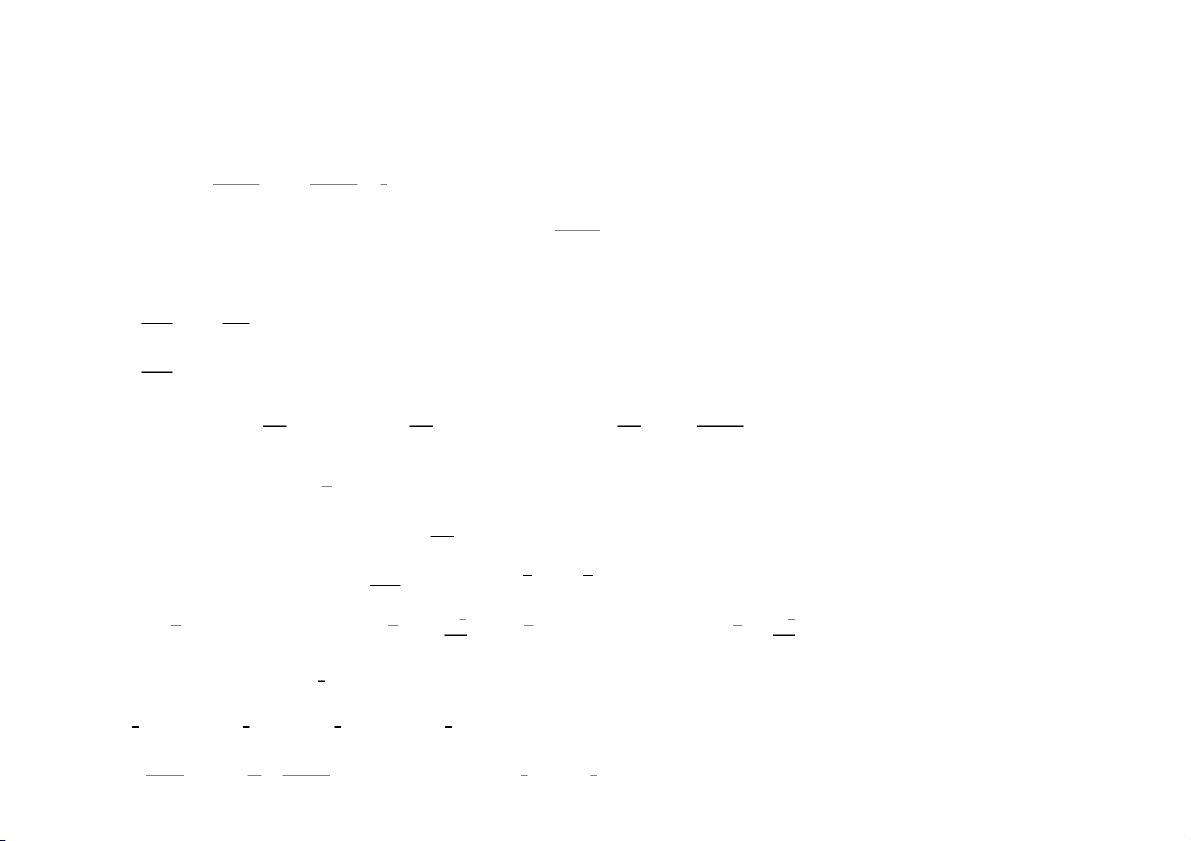
Preview text:

VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ 1 ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 –Học kì 20141
ĐỀ 2 ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 – Học kì 20141
Khóa 59 - Thời gian làm bài: 60 phút
Khóa 59 - Thời gian làm bài: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký
xác nhận số đề vào bài thi
xác nhận số đề vào bài thi  
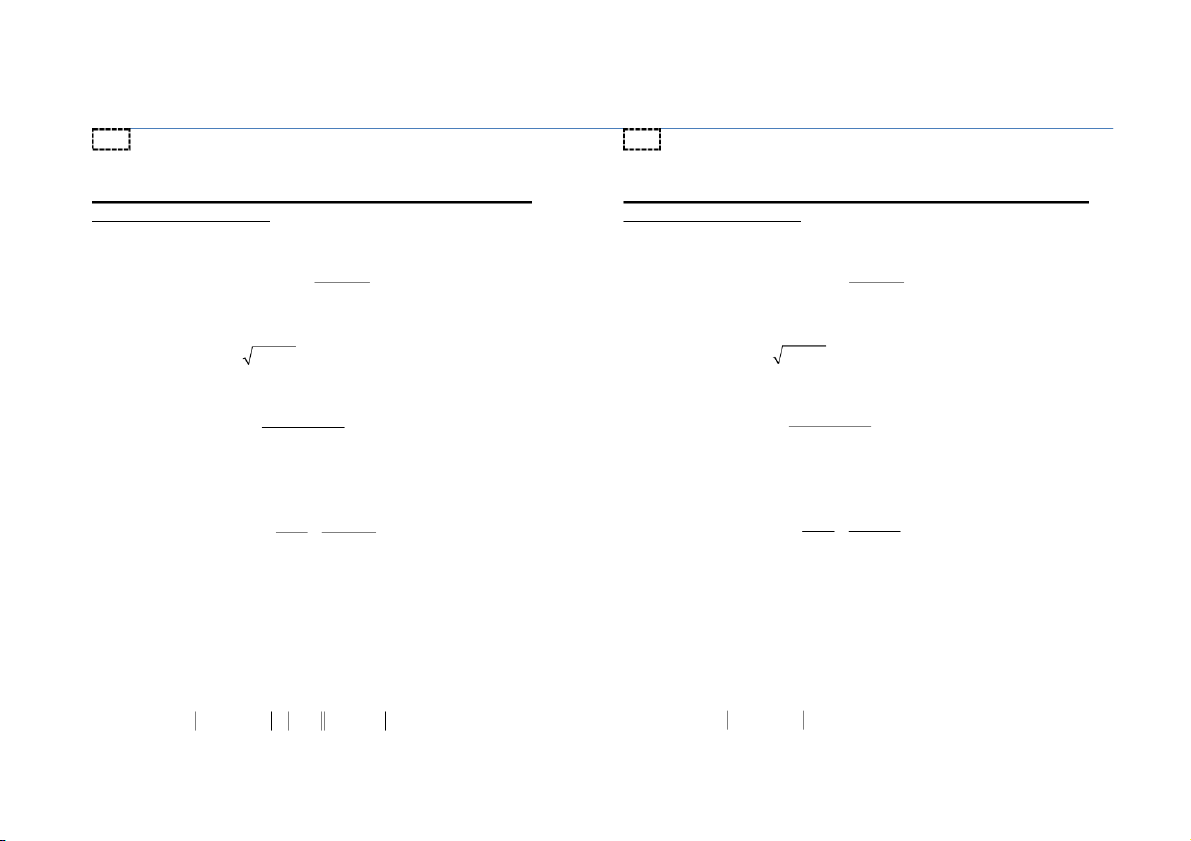
Câu 1 (1 điểm). Tìm giới hạn lim  .
Câu 1 (1 điểm). Tìm giới hạn lim . →  → ()
Câu 2 (1 điểm). Khi  → 0, các VCB () =  − ln(1 + ) và
Câu 2 (1 điểm). Khi  → 0, các VCB () =  − arctan  và
() =   có tương đương không?
() =  có tương đương không?  
Câu 3 (1 điểm). Điểm  = 0 là điểm gián đoạn loại gì của hàm số sau
Câu 3 (1 điểm). Điểm  = 0 là điểm gián đoạn loại gì của hàm số sau 1 2 1 3  = arctan .  = arcsin .   + 1   + 1
Câu 4 (1 điểm). Tính đạo hàm cấp 100 của hàm số sau
Câu 4 (1 điểm). Tính đạo hàm cấp 100 của hàm số sau  = ( + 1) sin .  = ( + 1) cos .
Câu 5 (1 điểm). Sử dụng vi phân, tính gần đúng giá trị  = ..
Câu 5 (1 điểm). Sử dụng vi phân, tính gần đúng giá trị  = ..
Câu 6 (1 điểm). Tìm cực trị của hàm số sau
Câu 6 (1 điểm). Tìm cực trị của hàm số sau 2 3  = .  = .  + 3  + 2
Câu 7 (2 điểm). Tính các tích phân sau
Câu 7 (2 điểm). Tính các tích phân sau a) ∫  .
b) ∫( + 1) cos  . a) ∫  .
b) ∫( + 2) sin  .  
Câu 8 (1 điểm). Cho () là hàm số khả vi tại 1 và biết rằng
Câu 8 (1 điểm). Cho () là hàm số khả vi tại 1 và biết rằng
(1 + 7) − (1 + 2)
(1 + 5) − (1 + 3) lim = 2. lim = 1. →  →  Tìm (1). Tìm (1).
Câu 9 (1 điểm). Tìm ,  ∈  sao cho
Câu 9 (1 điểm). Tìm ,  ∈  sao cho
li  − 1 +  + 
ln(1 + 3) +  +   m → = 0. lim → = 0.   CuuDuongThanCong.com
https://fb.com/tailieudientucntt
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ 3 ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 –Học kì 20141
ĐỀ 4 ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 – Học kì 20141
Khóa 59 - Thời gian làm bài: 60 phút
Khóa 59 - Thời gian làm bài: 60 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký
xác nhận số đề vào bài thi
xác nhận số đề vào bài thi
Câu 1 (2 điểm). Tìm các giới hạn sau
Câu 1 (2 điểm). Tìm các giới hạn sau     a) lim . b) lim(1 + 2). a) lim .
b) lim(1 − 3). →  → →  →
Câu 2 (1 điểm). Tìm và phân loại điểm gián đoạn của hàm số sau
Câu 2 (1 điểm). Tìm và phân loại điểm gián đoạn của hàm số sau arctan  sin   = .  = .  +   − 
Câu 3 (1 điểm). Cho hàm số () =  . Tính (0).
Câu 3 (1 điểm). Cho hàm số () =  . Tính (0).  
Câu 4 (1 điểm). Sử dụng vi phân, tính gần đúng giá trị  = √  1.02.
Câu 4 (1 điểm). Sử dụng vi phân, tính gần đúng giá trị  = √  1.01.
Câu 5 (1 điểm). Tìm cực trị của hàm số sau
Câu 5 (1 điểm). Tìm cực trị của hàm số sau  + 3  + 2  = .  = . 2 3
Câu 6 (2 điểm). Tính các tích phân sau
Câu 6 (2 điểm). Tính các tích phân sau
a) ∫( + 1). b) ∫  .
a) ∫( + 3). b) ∫  .   Câu 7 (1 điểm). Cho Câu 7 (1 điểm). Cho () − 5 () + 3 lim = 2. lim = 1. →  − 1 →  − 2 Tìm lim(). Tìm lim(). → →
Câu 8 (1 điểm). Tìm các tiệm cận của hàm số sau
Câu 8 (1 điểm). Tìm các tiệm cận của hàm số sau 2 1  =  sin .  =  sin .   CuuDuongThanCong.com
https://fb.com/tailieudientucntt
VIÞN TOÁN þNG DþNG VÀ TIN HÞC
VIÞN TOÁN þNG DþNG VÀ TIN HÞC
Þ 5 Þ THI GIþA Kþ MÔN GI¾I TÍCH 1 3 Hßc kì 20141
Þ 6 Þ THI GIþA Kþ MÔN GI¾I TÍCH 13 Hßc kì 20141
Khóa: K59 Thßi gian: 60 phút
Khóa: K59 Thßi gian: 60 phút
Chú ý: Thí sinh không ±ÿc sÿ dÿng tài lißu và giám thß ph¿i ký
Chú ý: Thí sinh không ±ÿc sÿ dÿng tài lißu và giám thß ph¿i ký
xác nh¿n sß ß vào bài thi
xác nh¿n sß ß vào bài thi
Câu 1. Tìm t¿p xác ßnh cÿa hàm sß y = arcsin (2x + ) 1 .
Câu 1. Tìm t¿p xác ßnh cÿa hàm sß y = arccos(12 2x ) . ù12 cos 2 x ù1 2 cos 4x
Câu 2. Tìm m ß hàm sß ü khi x b 0, ü khi x b 0, 2 f (x) = ú x
liên tÿc t¿i x = 0.
Câu 2. Tìm m ß hàm sß 2 f (x) = ú x liên tÿc t¿i x = 0. üm khi x û = 0 üm khi x û = 0 Câu 3. Khi x 0+ ³
c¿p vô cùng bé sau có t±¡ng ±¡ng không?
Câu 3. Khi x ³ 0 c¿p vô cùng bé sau có t±¡ng ±¡ng không? 3 2 ( ³ )
x = x + x và sin ´ ( ) x x = e 2 cos2 x . 3 4 3 (
³x) = x + x và tan ´( ) x x = e 2 cos4x .
Câu 4. Tìm cÿc trß cÿa hàm sß f (x) = ln(x + 2) 2 x .
Câu 4. Tìm cÿc trß cÿa hàm sß f( )
x = x 2ln( x + 3) . (x + 1)dx x + dx
Câu 5. Tính tích phân + .
Câu 5. Tính tích phân ( 2) + . (x + 2)(x + 3) (x + 3)(x + 4)
ù(22 x )(32 x) khi x f 3,
ù(32 x )(x 2 4) khi x f 4,
Câu 6. Tính f '(3) vßi f (x) = ú
Câu 6. Tính f '(4) vßi f (x) = ú x 2 3 khi x > 3. û 42 x khi x > 4. û û 2 þ û x 21 1 þ Câu 7. x 2 1 Tính gißi h¿n lim 2 ü ÿ.
Câu 7. Tính gißi h¿n lim 2 ü ÿ. x³3 x ý 2 3 ln( x2 2) ø x³2 x ý 2 2 ln(x 21) ø
Câu 8. Tính tích phân arcsin xdx + .
Câu 8. Tính tích phân arccosxdx + .
Câu 9. Cho hàm sß f (x) liên tÿc trên [1, +> ) và kh¿ vi trên (1, +> )
Câu 9. Cho hàm sß f (x) liên tÿc trên (2> ,1] và kh¿ vi trên ( 2 > ,1)
thßa mãn lim f (x) = f (1) . Chÿng minh r¿ng tßn t¿i c > 1 sao cho
thßa mãn lim f (x) = f (1) . Chÿng minh r¿ng tßn t¿i c < 1 sao cho x³+> x³2> f '(c) = 0 . f '(c) = 0.
Câu 10. Tìm t¿t c¿ hàm sß f( )
x kh¿ vi trên = thßa mãn
Câu 10. Tìm t¿t c¿ hàm sß f( )
x kh¿ vi trên = thßa mãn f ( )
a 2 f (b) f a 2 b sin(a 2 ) b , a " ,b * . 2 = (a b )
f (a) 2 f (b) f|a 2 b | e 2 1|, a " ,b *=.
Thang ißm: Mßi câu 1 ißm.
Thang ißm: Mßi câu 1 ißm.
H¾T H¾T
H¾T CuuDuongThanCong.com
https://fb.com/tailieudientucntt
VIÞN TOÁN þNG DþNG VÀ TIN HÞC
VIÞN TOÁN þNG DþNG VÀ TIN HÞC
Þ 8 Þ THI GIþA Kþ MÔN GI¾I TÍCH 13 Hßc kì 20141
Þ 7 Þ THI GIþA Kþ MÔN GI¾I TÍCH 1 3 Hßc kì 20141
Khóa: K59 Thßi gian: 60 phút
Khóa: K59 Thßi gian: 60 phút
Chú ý: Thí sinh không ±ÿc sÿ dÿng tài lißu và giám thß ph¿i ký
Chú ý: Thí sinh không ±ÿc sÿ dÿng tài lißu và giám thß ph¿i ký
xác nh¿n sß ß vào bài thi
xác nh¿n sß ß vào bài thi
Câu 1. Tìm hàm sß ng±ÿc cÿa hàm sß 3x + 4 y = . 2 x + 3
Câu 1. Tìm hàm sß ng±ÿc cÿa hàm sß y = . 5x + 6 4 x + 5 1
Câu 2. Phân lo¿i ißm gián o¿n Ã
x = 0 cÿa hàm sß f ( x) = . cot
Câu 2. Phân lo¿i ißm gián o¿n 1 x =
cÿa hàm sß f ( x) = . 1 + 5 x 2 tan 1+ 4 x
Câu 3. Cho hàm sß 2 ( ) x
f x = xe . Tính ¿o hàm c¿p cao (6) f (x) .
Câu 3. Cho hàm sß 3 ( ) x
f x = xe . Tính ¿o hàm c¿p cao (5) f (x) .
Câu 4. Chÿng minh r¿ng ln(x + 1) f x,"x g 0.
Câu 4. Chÿng minh r¿ng 2
2x arctan x g ln(1+ x ), x " g 0.
Câu 5. Tính gißi h¿n tan lim(sin x) x . Ã
Câu 5. Tính gißi h¿n cot lim(cos x) x . x³ 2 x ³0
Câu 6. Tính tích phân Câu 6. arctan(3x )dx
Tính tích phân arctan(2x)dx + . + . x
e cosx 2 12 x x
e sin x 2 x
Câu 7. Tính gißi h¿n lim .
Câu 7. Tính gißi h¿n lim . 3 x³0 x 2 x ³0 x dx dx
Câu 8 . Tính tích phân
Câu 8. Tính tích phân + . + . 2 2 (x + 3) (x + 4) 2 2 (x + 2) (x + 3)
Câu 9. Tính ¿o hàm c¿p cao (17) y
(0) vßi y = arccosx .
Câu 9. Tính ¿o hàm c¿p cao (19) y
(0) vßi y = arcsin x . f x f x Câu 10. Cho hàm sß
Câu 10. Cho hàm sß f : ( 2>,0) ³ f và ' ( ) g 0 f : (0, + ) > ³ = thßa mãn ( ) 1
= thßa mãn f ( x) f 1 và f ' (x ) g 0
vßi mßi x < 0. Chÿng minh r¿ng f '(x) g 0 vßi mßi x < 0 .
vßi mßi x > 0. Chÿng minh r¿ng f '(x) f 0 vßi mßi x > 0 .
Thang ißm: Mßi câu 1 ißm.
Thang ißm: Mßi câu 1 ißm.
H¾T
H¾T CuuDuongThanCong.com
https://fb.com/tailieudientucntt
ĐÁP ÁN ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 – ĐỀ 1 Câu 1. lim   → =  (0.5đ+0.5đ)     Câu 2. L’Hospital lim ()  →  = lim→ (0.5đ)   = lim  → = 1. Hai VCB tương đương (0.5đ) 
Câu 3. lim  arctan  = lim  ×  = 2. (0.5đ) Điểm  = 0 là điểm gián đoạn bỏ được. (0.5đ) →   →  
Câu 4. Áp dụng CT Leibnitz () = ( + 1)(sin )() + 100( + 1)′(sin )() (0.5đ)
() = ( + 1) sin( + 50) + 100 sin( + ) = ( + 1) sin  − 100 cos . (0.5đ) 
Câu 5. Xét () = , () = . (0.5đ) Ta có  = (0.01) ≈ (0) + (0) × 0.01 =1.01 (0.5đ)
Câu 6. TXĐ: R. Đạo hàm  = .  = 0:  = −√3,  = √3. (0.5đ) ()
 = −√3 là điểm cực tiểu  = −√3 = − √.  = √3 là điểm cực đại  . (0.5đ)  Đ = √3 = √ 
Câu 7. a) ∫   = ∫   = ∫( +  + 1 +  ) (0.5đ)   
=   +   +  + ln | − 1| + . (0.5đ)  
b)  ∫( + 1)(1 + cos 2) =  ∫( + 1) +  ∫( + 1)(sin 2) (0.5đ)   
=   +   + ( + 1) sin 2 −  ∫ sin 2  =  +   + ( + 1) sin 2 +  cos 2 + . (0.5đ)        
Câu 8.  khả vi tại 1, nên (1) = lim ()(). (0.5đ) →  Ta có 2 = lim
()() → = lim
   − 2 ()() = 7(1) − 2(1) =   → 7 ( ) ( )  
5 (1). Suy ra (1) = . (0.5đ) 
Câu 8. Ta có 0 = lim→( × ) = lim +  + ) = 2 + . (0.5đ)  →( 
Suy ra  = −2.  = − lim   → = − lim = −2. (0.5đ)  → 
Cách 2 Dùng khai triển hữu hạn. CuuDuongThanCong.com
https://fb.com/tailieudientucntt
ĐÁP ÁN ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 – ĐỀ 2 Câu 1. lim   → =  (0.5đ+0.5đ) ()    Câu 2. L’Hospital lim    →  = lim→ (0.5đ)   = lim  → = 1. Hai VCB tương đương (0.5đ) 
Câu 3. lim  arctan  = lim  ×  = 3. (0.5đ) Điểm  = 0 là điểm gián đoạn bỏ được. (0.5đ) →   →  
Câu 4. Áp dụng CT Leibnitz () = ( + 1)(cos )() + 100( + 1)′(cos )() (0.5đ)
() = ( + 1) cos( + 50) + 100 cos( + ) = ( + 1) cos  + 100 sin . (0.5đ) 
Câu 5. Xét () = , ′() = . (0.5đ) Ta có  = (0.02) ≈ (0) + (0) × 0.02 =1.02 (0.5đ)
Câu 6. TXĐ: R. Đạo hàm  = .  = 0:  = −√2,  = √2. (0.5đ) ()
 = −√2 là điểm cực tiểu  √
 = −√2 = − √ .  = √2 là điểm cực đại  . (0.5đ) 
Đ = √2 =   
Câu 7. a) ∫   = ∫   = ∫( −  + 1 −  ) (0.5đ)   
=   −   +  − ln | + 1| + . (0.5đ)  
b)  ∫( + 2)(1 − cos 2) =  ∫( + 2) −  ∫( + 2)(sin 2) (0.5đ)   
=   +  −  ( + 2) sin 2 +  ∫ sin 2  =  +  −  ( + 2) sin 2 −  cos 2 + . (0.5đ)      
Câu 8.  khả vi tại 1, nên (1) = lim ()(). (0.5đ) →  Ta có 1 = lim
()() → = lim
   − 3 ()() = 5(1) − 3(1) =  → 5 ( ) ( )  
2(1). Suy ra (1) = . (0.5đ) 
Câu 8. Ta có 0 = lim→( × ()) = lim +  + ) = 3 + . (0.5đ)  →(()  
Suy ra  = −3.  = − lim ()  → = − lim = . (0.5đ)  →  
Cách 2 Dùng khai triển hữu hạn. CuuDuongThanCong.com
https://fb.com/tailieudientucntt
ĐÁP ÁN ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 – ĐỀ 3
Câu 1. a) lim  = lim  = 1 (0.5đ+0.5đ) →  →  ()
b) lim(1 + 2) =   () → (0.5đ) =  →  = . (0.5đ) →
Câu 2. Hàm số có 2 điểm gián đoạn  = 0 và  = −1
lim  = lim = 1. Điểm  = 0 là điểm gián đoạn bỏ được. (0.5đ) →  → 
lim  = ∞. Điểm  = −1 là điểm gián đoạn loại hai. (0.5đ) →  ()
Câu 3. Hàm () =  =  +  + 1 +  . Đạo hàm ()() =    = ! . (0.5đ)    ()
(0) = ()(0)() = −10!(). (0.5đ)
Câu 4. Xét hàm số () = √. Ta có (0.5đ)
 = (1.02) ≈ (1) + (1) × 0.02 = 1 + . ≈1.006667. (0.5đ) 
Câu 5. TXĐ:  ≠ 0. Đạo hàm  = .  = 0:  = −√3,  = √3. (0.5đ) 
 = −√3 là điểm cực đại Đ = −√3 = −√3.  = √3 là điểm cực tiểu  = √3 = √3. (0.5đ)
Câu 6. a) ∫( + 1) =  ∫( + 1)() (0.5đ) 
=  ( + 1) −  ∫  =  ( + 1) −  + . (0.5đ)    
b) ∫   = ∫(−  ) (0.5đ)
= 2 ln || −  ln | + 1| + . (0.5đ)     Câu 7. Ta có lim  
→(() − 5) = lim→( − 1) ( )
= 0 × 2 = 0 .(0.5đ) Suy ra lim  () = 5 . (0.5đ) →
Câu 8. lim→  = 0: hàm số không có tiệm cận đứng. lim  
→  = lim→  ×  sin  = ∞. lim = lim  = 2, đặt  =  (0.5đ)  →  →  sin   sin 2 lim( − 2) = lim 2 1 sin 2 − 2   sin → →  − 2 = lim →    − 2 = lim →  = 0.
Tiệm cận xiên  = 2. (0.5đ) CuuDuongThanCong.com
https://fb.com/tailieudientucntt
ĐÁP ÁN ĐỀ THI GIỮA KỲ MÔN GIẢI TÍCH 1 – ĐỀ 4
Câu 1. a) lim  = lim  =  (0.5đ+0.5đ) →  →   ()
b) lim(1 − 3) =   () → (0.5đ) =  →  =  (0.5đ) →
Câu 2. Hàm số có 2 điểm gián đoạn  = 0 và  = 1
lim  = lim = −1. Điểm  = 0 là điểm gián đoạn bỏ được. (0.5đ) →  → 
lim  = ∞. Điểm  = 1 là điểm gián đoạn loại hai. (0.5đ) →  ()
Câu 3. Hàm () =  =  −  + 1 −  . Đạo hàm ()() = −    = ! . (0.5đ)    ()
(0) = ()(0)() = −10!(). (0.5đ)
Câu 4. Xét hàm số () = √. Ta có (0.5đ)
 = (1.01) ≈ (1) + (1) × 0.01 = 1 + . = 1.0025. (0.5đ) 
Câu 5. TXĐ:  ≠ 0. Đạo hàm  = .  = 0:  = −√2,  = √2. (0.5đ) 
 = −√2 là điểm cực đại  √ √
Đ = −√2 = −  .  = √2 là điểm cực tiểu  .(0.5đ) 
 = √2 =   
Câu 6. a) ∫( + 3) =  ∫( + 3)() (0.5đ) 
=  ( + 3) −  ∫  =  ( + 3) −  + . (0.5đ)     b) ∫  ) ∫
 = ∫(  +  ) (0.5đ)
=  ln || + ln( + 2) + . (0.5đ)   ()   Câu 7. Ta có lim  
→(() + 3) = lim→( − 2) ( )
= 0 × 1 = 0. (0.5đ) Suy ra lim  () = −3. (0.5đ) →
Câu 8. lim→  = 0: hàm số không có tiệm cận đứng. lim  
→  = lim→  ×  sin  = ∞. lim = lim  = 1, đặt  =  (0.5đ)  →  →  sin   1 1 sin  sin  − 
lim ( − ) = lim   sin → →  − 1 = lim
→    − 1 = lim →  = 0. Tiệm cận xiên  = . (0.5đ) CuuDuongThanCong.com
https://fb.com/tailieudientucntt ÁP ÁN Þ 5
Câu 1. +) ißu kißn xác ßnh: 21f 2x + 1f 1, +) õ 21f x f 0. T¿p xác ßnh = [ 21,0] . 1 2cos2x
Câu 2. +) lim () = lim
= 2. +) Hàm sß liên tÿc t¿i = 0 õ = (0) = lim () = 2 . 2 ³0 ³0 ³ 0 Câu 3. Khi 0+ ³ : 3 2 +) (
³ ) = + ~ , +) sinx ´ () = ( 21) + (12 cos2x) , sinx 21 ~ sinx ~ , 2
1 2cos2x ~ 2x ó ´ () ~ . V¿y ( ³ ) ~ ( ´ ) . 1 2 21
Câu 4. +) > 2 2 , '() = 21 = = 0 õ = 21. + 2 + 2
+) Xét d¿u '() ta có () ¿t cÿc ¿i 1 t¿i = 1 2 . (+1)x þ 1 2 2 Câu 5. +) ù = = + x + +
,+) = 2ln | + 2 | 2
+ ln | + 3 | + . (2)(3)
ÿø 2 3ú + + + + û 2 3
(2 2 )(32 ) Câu 6. +) ' (3) = lim =1. +) ' (3) = lim =1. KL: ' ' '
(3) = (3) = (3) = 1. + + 2 2 + 2 ³3 2 3 ³ 3 2 3
(2 2)ln(2 2) 2 + 3
(2 2)ln(2 2) 2 + 3 ' ln(2 2) 1
Câu 7. +) = lim = lim , +)= lim = ³3 ³3 2 ( ³
2 3)ln [1 + (2 3)] (2 3) 3 2( 23) 2 Câu 8. +) arcsin = arcsin   2 + + ,+) 2
= arcsin+ 12 +. 2 12 û 1 Câu 9. +) Xét þ
() = , * (0,1] ü ÿ
(0) := lim ( ) = lim () = (1) ó (0) = (1) ý . ø , + 0 ³ ³+> 1
+) () thßa mãn ßnh lí Rolle trên [0,1] nên
# * (0,1) | '() = 0, =   = 0 0 ¿t ta có '( ) 0. 0 Câu10.+)"*
() 2 () f 2 sin(2 ) , "b 0 = , 0 0 0 0
() 2 ()
() 2 () 0 0 ó
f sin( 2 ) , "b ó '( ) = lim =0 0 0 0 2 ³ 0 2 . 0 0 c ó = + ) ' 0 o
ns(thßa mãn).
Thang ißm: mßi d¿u +) là 0,5 ißm CuuDuongThanCong.com
https://fb.com/tailieudientucntt ÁP ÁN Þ 6
Câu 1. +) ißu kißn xác ßnh: 21f 12 2x f 1 , +) õ 0 f x f1. T¿p xác ßnh = [0,1]. 1 2cos4x
Câu 2. +) lim () = lim
= 8. +) Hàm sß liên tÿc t¿i = 0 õ = (0) = lim () = 8 . 2 ³0 ³0 ³ 0
Câu 3. Khi ³ 0: 3 4 3 +) (
³) = + ~ , +) tan x ´ ()= ( 2 1)+ (12 cos4x), tanx 1 2 ~ tan x ~ , 2
1 2cos4x ~ 8x ó ´ () ~ . V¿y ( ³ ) ~ ( ´ ) . 1 + 2
Câu 4.+) > 23, '() = 12 = = 0 õ = 22. + 3 + 3
+) Xét d¿u '() ta có () ¿t cÿc tißu 22 t¿i = 2 2 . (+2)x þ 1 2 2 Câu 5. +) ù = = + x + +
,+) = 2ln | + 3| +2ln | + 4 | +. (3)(4)
ÿø 3 4ú + + + + û 4 2
(3 2 )(24)
Câu 6. +) '(4) = lim = 1 2 . +) ' (4) = lim = 21. KL: ' ' '
(4) = (4) = (4) = 21. + + 2 2 + 2 ³4 2 4 4 ³ 2 4
( 21)ln( 2 1) 2 + 2
( 21)ln( 21) 2 + 2 ' ln( 21) 1
Câu 7. +) = lim = lim , +) =lim = ³2 ³2 2 ( 2 ³
2 2) ln [1+ (2 2)] (2 2) 2(2 2) 2 Câu 8. +) arccos = arccos   + + + ,+) 2
= arccos2 12 + 2 . 1 2 û 1 Câu 9. +) Xét þ
() = + 2 , * [2 1,0) ü ÿ
(0) := lim () = lim () = (1) ó (0) = (21) ý ø , . ³02 ³2> 1
+) () thßa mãn ßnh lí Rolle trên [ 21,0] nên #* (2 1,0) | '()= 0, '( + 2) = 0 0 0 ta có . 0 Câu10.+)" * ( ) 2 ( ) 2     f 2   2 1 , " b 0 = , 0 0 0 0
() 2 () 2
() 2 () 0   0 0 ó f 21 ,
" b ó '() = lim = 0 0 0 2 ³ 0 2 . 0 0 c ó = + ) ' 0 o
ns (thßa mãn).
Thang ißm: mßi d¿u +) là 0,5 ißm CuuDuongThanCong.com
https://fb.com/tailieudientucntt ÁP ÁN Þ 7 5 2x + 3 3 25û 1 3 25û 1 Câu 1. +) þ þ b 2 , = õ = , b
.+) Hàm sß ng±ÿc c¿n tìm: = , b . 4 4x 5 4 ü ÿ + ü ÿ 2 2 ý 2 ø 42 2 ý 2 ø Ã
Câu 2. +) lim () = 0, lim () = 1. +) lim ( ) b lim ( ) ó =
là ißm gián o¿n lo¿i 1. Ã 2 Ã + Ã + Ã2 ³ ³ 2 ³ ³ 2 2 2 2
Câu 3. +) (  )(5) 3x 3x (5) 1 3x (4)
= () + ()'() , +) 5 3x 4 3x
= 3  + 5.3 . 5
Câu 4. +) Xét hàm sß 2
() = 2arctan 2 ln(1 +), g 0 , '( ) = 2 arctan > 0, "> 0.
+) ó () ßng bi¿n khi g 0 ó ()g (0)= 0, " g 0. lim cotln cos Câu 5. +) cot cot ln cos 0
= lim(cos ) = lim = ³ . ³0 ³0 ' ln cos 2tan +) lim cot lncos = lim = lim
= 0, ó =1. t anx 1 ³ 0 ³ 0 ³ 0 2 cos 2xdx 1 Câu 6. +) 2
= arctan(2) = arctan(2) 2
, +) = arctan(2) 2 ln(1+ 4x ) + . + + . 2 1 +4x 4 ' '
sin 2
sin + cos 1 2 2 cos Câu 7. +) lim = lim , +) = lim = 1. 2 0 ³ 0 ³ 0 2 ³ 2 û þ Câu 8. +) x 1 2 1 2 1 1 =  + + , +) =  2ln|x+2| +2ln|x+3|+C. + + 2 2 ( ü ÿ
+ 2) ( +3) (x+2)² x+2 (x+3)² x+3 +2 +3 ý ø 1 2 Câu 9. +) 2 2 2 2 ' =
ó (12 )' = 12 ó (12 )'2 2 '=
= 2  'ó (12 )'2  '= 0. 2 2 1 2 1 2 +) ó ( 2 2 )() 2 2 (+2) ( 1 + ) ( 1 + ) (1 ) ' ' = 0 ó (1 2 ) 2 .2x. 2 ( 2 1) 2 .      2  = 0, + ó =   ó = = ï= ( )2 = ( )2 ( 2) 2 ( ) (19) 2 (17) (0) (0) (0) 17 (0) 17!! '(0) 17!! . Câu 10.
+) Ph¿n chÿng, gi¿ sÿ có > 0 sao cho '() > 0 . Do ' () g 0 nên '() g '(), " > . 0 0 0 0 ³+>
+) Theo Lagrange: # *( , ) | ( ) = ( ) + '( )( 2 ) g ( ) + '( )( 2 ) ³ + > > 1            (trái gt). 0 0 0 0 0 0
Thang ißm: mßi d¿u +) là 0,5 ißm CuuDuongThanCong.com
https://fb.com/tailieudientucntt ÁP ÁN Þ 8 6 3x + 4 42 6û 3 4 2 6û 3 Câu 1. +) þ þ b 2 , = õ = , b
.+) Hàm sß ng±ÿc c¿n tìm: = , b . 5 5x 6 5 ü ÿ + ü ÿ 2 3 ý 5 ø 5 23 ý 5 ø
Câu 2. +) lim () = 0, lim () = 1. +) lim ( )
b lim ( )
ó = 0 là ißm gián o¿n lo¿i 1. 0+ 02 ³ ³ 0 + 0 2 ³ ³
Câu 3. +) (  )(6) 2x 2x (6) 1 2x (5) = (   ) + ( ) '( ) , +) 6 2x 5 2x
= 2  + 6.2 . 6 1
Câu 4. +) Xét hàm sß
2 ln(+ 1),g 0. '() = 12 = g 0. + 1 + 1
+) ó () ßng bi¿n, ( )
g (0) = 0, " g 0 .
lim tan lnsin à Câu 5. +) tan tan lnsin ³
= lim(sin ) 2 = lim = . Ã Ã ³ ³ 2 2 +) ' ln sin cot
lim tan lnsin = lim = lim
= 0, ó =1. Ã Ã cotx 1 Ã ³ ³ ³ 2 2 sin 2 2 2 3xdx 1 Câu 6. +) 2
= arctan(3) = arctan(3) 2
, +) = arctan(3) 2 ln(1+ 9x ) + . + + 2 1+ 9x 6 ' ' 2 2 2 2 2 Câu 7. +)
cos 1 cos sin 1 2si n 1 lim =lim , ) + =lim = 2 . 3 2 ³ 0 ³ 0 ³ 0 3 6 3 û þ Câu 8. +) x 1 2 1 2 1 1 =  + + , +) =  2ln|x+3| +2ln|x+4|+C. + 2 2 + ( ü ÿ
+ 3) (+ 4) (x+3)² x+3 (x+4)² x+4 + 3 + 4 ý ø 1 Câu 9. +) 2 2 2 2 2 ' =
ó (12 )'= 2 12 ó (12 )'2 2 '=
= 2  'ó (12 )'2  '= 0. 2 2 1 2 1 2 +) ó ( 2 2 )( ) 2 2 ( 2 + ) ( 1 + ) ( 1 + ) (1 ) ' ' = 0ó (12 ) 2 .2x. 2 ( 2 1) 2 .      2  = 0, + ó =   ó = = ï = ( )2 = 2 ( )2 ( 2) 2 ( ) (17) 2 (15) (0) (0) (0) 15 (0) 15!! '(0) 15!! . Câu 10.
+) Ph¿n chÿng, gi¿ sÿ có
0 sao cho '() 0 . Do ' () 0 nên   0 0 '( ) '( ), . 0 0 ³2>
+) Theo Lagrange: #*( ,  ) | ( )
= ( ) + '( )
( 2 ) g ( ) + '( )( 2 ) ³ + > > 1(trái gt). 0 0 0 0 0 0
Thang ißm: mßi d¿u +) là 0,5 ißm CuuDuongThanCong.com
https://fb.com/tailieudientucntt