Đề thi giữa kỳ 2 Toán 12 năm 2020 – 2021 trường Đoàn Thượng – Hải Dương

SỞ GD VÀ ĐT HẢI DƯƠNG
ĐỀ KIỂM TRA GIỮA KÌ 2 NĂM HỌC 2020 – 2021
TRƯỜNG THPT ĐOÀN THƯỢNG Môn: TOÁN 12 Đề số 1
Thời gian làm bài: 90 phút
I). Phần trắc nghiệm (7 điểm). Câu 1.
Họ nguyên hàm của hàm số f  x 3  2x  9 là: 1 1 A. 4 x  9x  C . B. 4 4x  9x  C . C. 4 x  C . D. 3 4x  9x  C . 2 4 Câu 2.
Họ nguyên hàm của hàm số f  x 2  3x  cos x là A. 3 x  cos x  C . B. 3 x  sin x  C . C. 3 x  cos x  C . D. 3 3x  sin x  C . Câu 3. Nguyên hàm sin d x x  bằng: 1 A.  cos x  C . B. cos x  C . C. cos 2x  C . D.  cos 2x  C . 2 Câu 4.
Tất cả nguyên hàm của hàm số f  x 1  là 2x  3 1 1 1 A. ln 2x  3  C . B. ln 2x  3  C . C. ln 2x  3  C . D. ln 2x  3  C . 2 2 ln 2 Câu 5.
Họ nguyên hàm của hàm số   3x f x  e là: 1 1 A. 3 x e  C B. x e  C C. 3x e  C D. 3 3 x e  C 3 3 Câu 6. Hàm số F  x 1
 4x  là một nguyên hàm của hàm số nào sau đây? x 1 1 A. f  x  4   C . B. f  x  4  . 2 x 2 x 1 C. f  x  4  . D. f  x 2  2x  ln | x | C . 2 x
Câu 7: Tìm nguyên hàm của hàm số f  x  cos3x . 1 A. cos 3x dx  sin 3x  C  . B. cos3x dx  sin 3x  C  . 3 1 C. cos 3x dx  3sin 3x  C  .
D. cos 3x dx   sin 3x  C  . 3
Câu 8: Hàm số F  x  cos3x là nguyên hàm của hàm số: x A. f  x sin 3  . B. f  x  3
 sin 3x . C. f x  3sin 3x . D. f  x  sin 3x . 3
Câu 9. Cho hàm số f  x thỏa mãn f  x  3  5cos x và f 0  5 . Mệnh đề nào dưới đây đúng?
A. f  x  3x  5sin x  2 .
B. f x  3x  5sin x  5 .
C. f x  3x  5sin x  5 .
D. f x  3x  5sin x  5.
Câu 10. Tìm họ nguyên hàm của hàm số   5x f x  . A.   d  5x f x x  C . B.   d  5x f x x ln 5  C . x x 1 5  C. f  x 5 dx   C . D. f  xdx   C . ln 5 x 1
Câu 11. Họ nguyên hàm của hàm số f  x  x  sin 2x là 2 x 2 x 1 A.  cos 2x  C . B.  cos 2x  C . 2 2 2 2 x 1 C. 2 1 x  cos 2x  C . D.  cos 2x  C . 2 2 2
Câu 12. Cho biết F  x là một nguyên hàm của hàm số f  x . Tìm I  2 f  x1dx  .
A. I  2F  x 1 C .
B. I  2xF  x 1 C .
C. I  2xF  x  x  C .
D. I  2F  x  x  C . 2  1  Câu 13: Tích phân I   2 dx   bằng  x  1 A. I  ln 2  2 . B. I  ln 2  1 . C. I  ln 2 1. D. I  ln 2  3 . 2 2 Câu 14: Tích phân dx  bằng. 2x 1 0 1 A. 2ln 5 . B. ln 5 . C. ln 5 . D. 4ln 5 . 2  3 dx Câu 15: Tích phân I   bằng? 2  sin x 4         A. cot  cot . B. cot  cot . C.  cot  cot . D.  cot  cot . 3 4 3 4 3 4 3 4  3
Câu 16: Tích phân f  x  cos d x x  bằng 0 1 1 A. B. 3 C. 3  D.  2 2 2 2 10 6
Câu 17. Cho hàm số f  x liên tục trên 0;10 thỏa mãn f  xdx  7 , f  xdx  3. Tính 0 2 2 10 P  f  xdx  f  xdx . 0 6 A. P  4 . B. P  4 . C. P  5 . D. P  7 . 1
Câu 18: Cho hàm số y  f  x có đạo hàm liên tục trên đoạn  1  ;  1 thỏa mãn f   xdx  5 và 1  f   1  4. Tìm f   1 . A. f   1  1  . B. f   1 1. C. f   1  9 . D. f   1  9  .
Câu 19: Cho hàm số y  f  x liên tục trên đoạn a;b . Mệnh đề nào dưới đây sai? b b b a A. f  xdx  f  tdt . B. f  xdx   f  xdx. a a a b b b c b C. kdx  k 
a  b , k   . D. f  xdx  f  xdx  f  xdx. a a a c
Câu 20: Cho hàm số y  f  x thoả mãn điều kiện f  
1  12 , f  x liên tục trên  và 4 f 
 xdx 17 . Khi đó f 4 bằng 1 A. 5 B. 29 C. 19 D. 9 1 3 3
Câu 21. Cho hàm số f  x liên tục trên  và có f  xdx  2; f
 xdx  6. Tính I  f  xdx . 0 1 0 A. I  8 . B. I 12 . C. I  36 . D. I  4 . 1 2x  3 Câu 22: Biết tích phân dx  a ln 2  b 
( a , b   ), giá trị của a bằng: 2  x 0 A. 7 B. 2 C. 3 D. 1 5 3 Câu 23. Biết rằng
dx  a ln 5  b ln 2 a,b  Z 
. Mệnh đề nào sau đây đúng? 2   x  3x 1 A. a  2b  0 . B. 2a  b  0 . C. a  b  0 . D. a  b  0 . 9 5
Câu 24: Biết f  x là hàm số liên tục trên  và f
 xdx  9. Khi đó tính I  f  3x6dx. 0 2 A. I  27 . B. I  24 . C. I  3 . D. I  0 . π 2 u   x Câu 25: Tính tích phân 2 I  x cos 2 d x x  bằng cách đặt 
. Mệnh đề nào dưới đây đúng? dv  cos 2 d x x 0  π 1 π 1 A. 2 π I  x sin 2x  x sin 2 d x x 2 π I  x sin 2x  2 x sin 2 d x x 0  . B.  . 2 0 2 0 0 π 1 π 1 C. 2 π I  x sin 2x  2 x sin 2 d x x 2 π I  x sin 2x  x sin 2 d x x 0  . D.  . 2 0 2 0 0
Câu 26: Trong không gian với hệ trục tọa độ Oxyz , các véctơ đơn vị trên các trục Ox , Oy , Oz lần   
lượt là i , j , k , cho điểm M 2; 1  ; 
1 . Khẳng định nào sau đây là đúng?                 A. OM  k  j  2i .
B. OM  2k  j  i . C. OM  2i  j  k . D. OM  i  j  2k . 
Câu 27: Trong không gian Oxyz , cho hai điểm A1;2; 4   và B 3
 ;2;2. Toạ độ của AB là A.  2  ;4; 2   . B.  4  ;0;6 . C. 4;0; 6   . D.  1  ;2;  1 .  
Câu 28: Trong không gian Oxyz cho A 1
 ; 2; 3, B1; 0; 2. Tìm điểm M thỏa mãn AB  2.MA ?  7   7  A. M 2;3;   . B. M 2;3;7 . C. M  4  ;6;7 . D. M 2; 3;   .  2   2 
Câu 29: Trong không gian Oxyz , phương trình mặt cầu tâm I 1; 2; 3 và bán kính R  3 là: A. 2 2 2
x  y  z  2x  4y  6z  5  0 .
C.  x  2   y  2   z  2 1 2 3  9 .
B.  x  2   y  2   z  2 1 2 3  9 .
D.  x  2   y  2   z  2 1 2 3  3.
Câu 30: Trong không gian Oxyz mặt cầu S có tâm I 1; 3  ; 
2 và đi qua A5;1;4 có phương trình:
A. x 2 y  2 z 22 1 3  24 .
B. x  2 y 2 z  22 1 3  24 .
C. x  2 y 2 z  22 1 3  24 .
D. x 2 y  2 z 22 1 3  24 .
Câu 31. Trong không gian Oxyz cho mặt phẳng P : x  2y  3z  3  0. Trong các véctơ sau véc tơ
nào là véctơ pháp tuyến của P ?     A. n  1;2;3 . B. n  1;2; 3   . C. n  1;2;3 . D. n   1  ;2;3 .
Câu 32: Trong không gian Oxyz , mặt phẳng đi qua điểm A2;  3;  2 và có một vectơ pháp tuyến n  2; 5  ;  1 có phương trình là
A. 2x  5y  z 17  0
B. 2x  5y  z 17  0
C. 2x  5y  z 12  0
D. 2x  3y  2z 18  0
Câu 33: Trong không gian với hệ toạ độ Oxyz , cho mặt phẳng P : 2x  y  2z  4  0 và điểm
A(1; 2; 2) . Tính khoảng cách d từ A đến mặt phẳng  P . 4 8 2 5 A. d  . B. d  . C. d  . D. d  . 3 9 3 9
Câu 34: Trong không gian Oxyz , mặt phẳng đi qua điểm M 1;2;5 và vuông góc với hai mặt
phẳng x  2 y  3z 1  0 và 2x  3y  z 1  0 có phương trình là
A. x  y  z  2  0 .
B. 2x  y  z 1  0 . C. x  y  z  2  0 .
D. x  y  z  6  0 .
Câu 35: Trong không gian Oxyz , viết phương trình mặt phẳng đi qua ba điểm A1;1;4 , B2;7;9 , C 0;9;13 . A. 2x  y  z 1  0 B. x  y  z  4  0
C. 7x  2 y  z  9  0 D. 2x  y  z  2  0
II). Phần tự luận (3 điểm). 1  x 1 
Câu 1: (1 điểm) Tính tích phân 2 I  3x  e  dx   .  x 1 0
Chú ý: Không chấp nhận HS bấm máy tính để viết ngay kết quả.
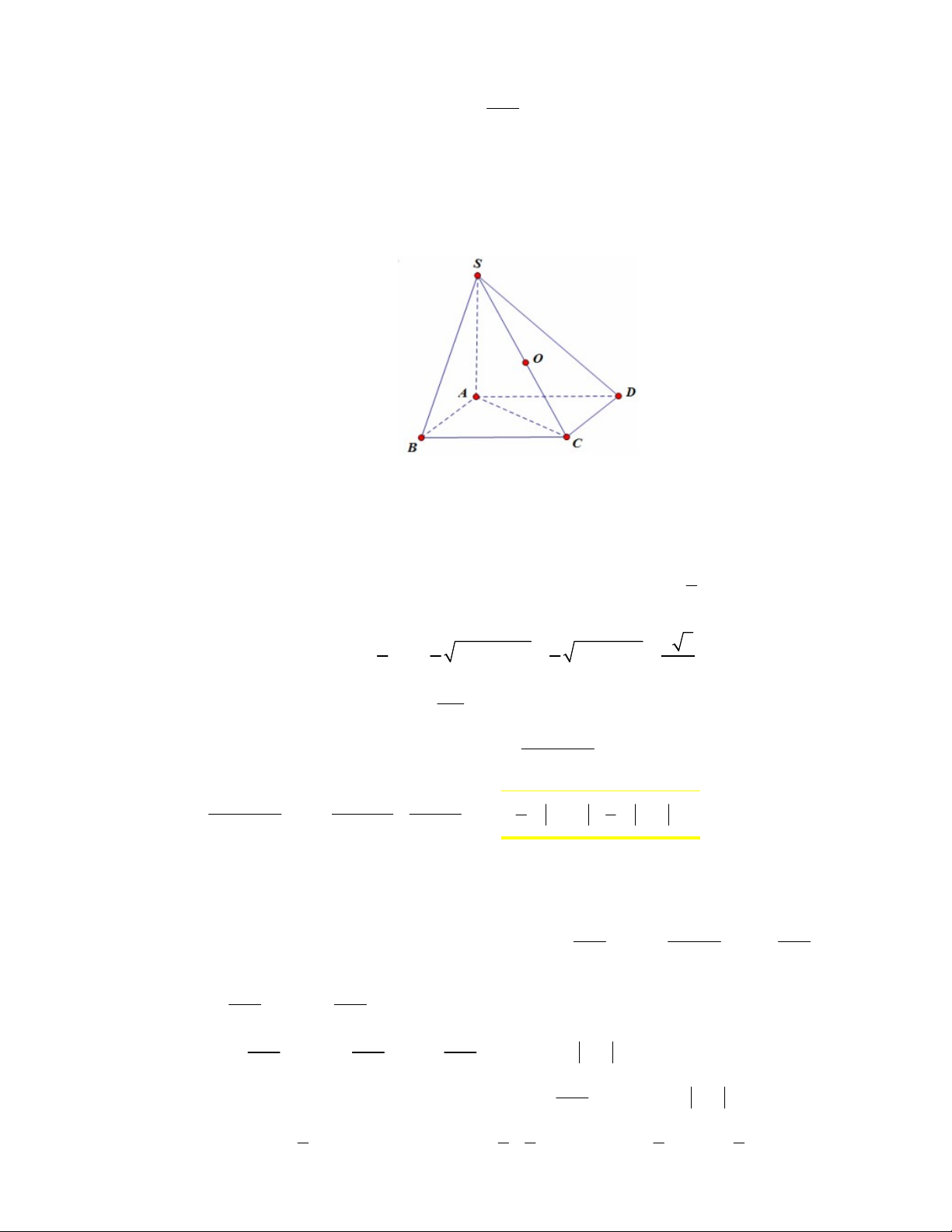
Câu 2: (1 điểm) Hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng
 ABCD và SA  2a . Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABCD . 2x  3
Câu 3: (0,5 điểm) Tìm họ nguyên hàm của hàm số dx  . 2 2x  x 1
Câu 4: (0,5 điểm) Cho hàm số y  f  x liên tục trên  \0;  
1 thỏa mãn điều kiện f   1  2ln 2
và x  x   f  x  f  x 2 1 .
 x  x . Giá trị f 2  a  bln 3 , với a,b . Tính 2 2 a  b . HƯỚNG DẪN GIẢI 1  x 1 
Câu 1: (1 điểm) Tính tích phân 2 I  3x  e  dx   .  x 1 0
Chú ý: Không chấp nhận HS bấm máy tính để viết ngay kết quả.
Câu 2: (1 điểm) Hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng
 ABCD và SA  2a . Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABCD . Lời giải Ta chứng minh được:
 BC  SAB  BC  SB  ΔSBC vuông tại B .
 CD  SAD  CD  SD  ΔSCD vuông tại D .
 SA   ABCD  SA  AC  ΔSAC vuông tại A . 1
Gọi O là trung điểm cạnh SC . Khi đó: OA  OC  OD  OB  OS  SC . 2
Do đó O là tâm mặt cầu ngoại tiếp khối chóp S.ABCD . 1 1 1 a 6 Bán kính mặt cầu là: 2 2 2 2 R  SC  SA  AC  4a  2a  . 2 2 2 2 2 3a Diện tích mặt cầu: 2 2 S  4πR  4π.  6πa . 2 2x  3
Câu 3: (0,5 điểm) Tìm họ nguyên hàm của hàm số dx  . 2 2x  x 1 Lời giải 2x  3 4  5 dx  (  )dx    2 5
 ln 2x 1  ln x 1  C 2 2x  x 1 3(2x 1) 3(x 1) 3 3
Câu 4: (0,5 điểm) Cho hàm số y  f  x liên tục trên  \0;  
1 thỏa mãn điều kiện f   1  2ln 2
và x  x   f  x  f  x 2 1 .
 x  x . Giá trị f 2  a  bln 3 , với a,b . Tính 2 2 a  b . Hướng dẫn giải x 1 x
Từ giả thiết, ta có x  x   f  x  f  x 2 1 .  x  x  . f  x  f x  2   x 1 x  1 x 1 x    x  . f x   , với x    \0;   1 .  x 1    x 1 x x x Suy ra . f  x  dx  hay
. f  x  x  ln x 1  C . x 1 x 1 x 1 x Mặt khác, ta có f  
1  2ln 2 nên C  1. Do đó
. f  x  x  ln x 1 1. x 1 2 3 3
Với x  2 thì . f 2 1 ln 3  f   3 3
2   ln 3 . Suy ra a  và b   . 3 2 2 2 2 9 Vậy 2 2 a  b  . 2