THE INTERNATIONAL UNIVERSITY (IU) Course: Engineering Probability and Statistics
Department of Industrial and Systems Engineering MIDTERM EXAMINATION
ENGINEERING PROBABILITY AND STATISTICS Duration: 120 minutes
Head of the Department of Lecturers: Student ID: Date: ISE November 5th, 2015 Dr. Ha Thi Xuan Chi Name:
Ass. Prof. Ho Thanh Phong Dr. Phan Nguyen Ky Phuc Ho Thanh Vu INSTRUCTIONS: 1.
This is a closed book examination. Only 2 A4 papers of note are allowed. 2.
Table of Normal Distribution is allowed. 3. Calculator is allowed. 4.
Laptop, mobile phone, discussion and materials transfer are strictly prohibited. 5.
There are partial credits, therefore show your work and logic when solving problems. Total
pages: 03 (including this page)
1. Coca 3 Cola Company wants to perform testing on Coke bottles volume. A sample of 10 bottles are
collected and volume of coke inside are measured. Specific data on coke volume are given as follow (in ml):
495; 502; 508; 483; 501; 497; 498; 497; 485; 501 a.
Find the value of 27th , and the 64th percentile
b. Find the upper and lower quartile and calculate the interquartile range
c. Find mean and variance of the data set
2. Quality Assurance Department of company Taone - a direct rival of the famous company Nokia, has
stated that 9% of their phones are defective.
a. If a customer randomly buy 10 of their phones, what is the probability that customer can find at least 8 working phone?
b. Assume that they ship phones in lots. If there are 10 lots in a shipment, what is the probability
at least 2 lots will have at most 7 working phones among 10 randomly selected phones.
c. The Quality Assurance Department now correct their own statement after a crisis in operation
system of their phones. Beside the 9% completely defective, now they also have 31% of their
phones are software broken but still repairable.
Given those conditions, what is the probability that exactly 4 phones are working among 10 randomly selected phones?
Engineering Probability and Statistics – Midterm Exam
THE INTERNATIONAL UNIVERSITY (IU) Course: Engineering Probability and Statistics
Department of Industrial and Systems Engineering
3. A 1st process creates shafts with defective rate 20%. For each defective item, we lost $2. The
company is considering the 2nd process. In this process, shafts can be machined twice. In the 1st
step, the diameter of the shaft in follows normal distribution with parameters N 100, 0.5. The
tolerance for the diameter of the shaft is100 0.5. Shafts satisfying the tolerance are not machined
again. Shafts which are reparable, i.e., at first their diameters are not lied within the tolerance but
they can be machined again to satisfy the tolerance, are turned the second time. This 2nd machining
costs 0.3 for each shaft. The rest is classified as irreparable.
a. Assume that company adopts the 1st process. Find the probability that in 20 shafts, we have at most 3 defectives.
b. Compare the expected costs between the 1st and 2nd process, when 1000 shafts are manufactured.
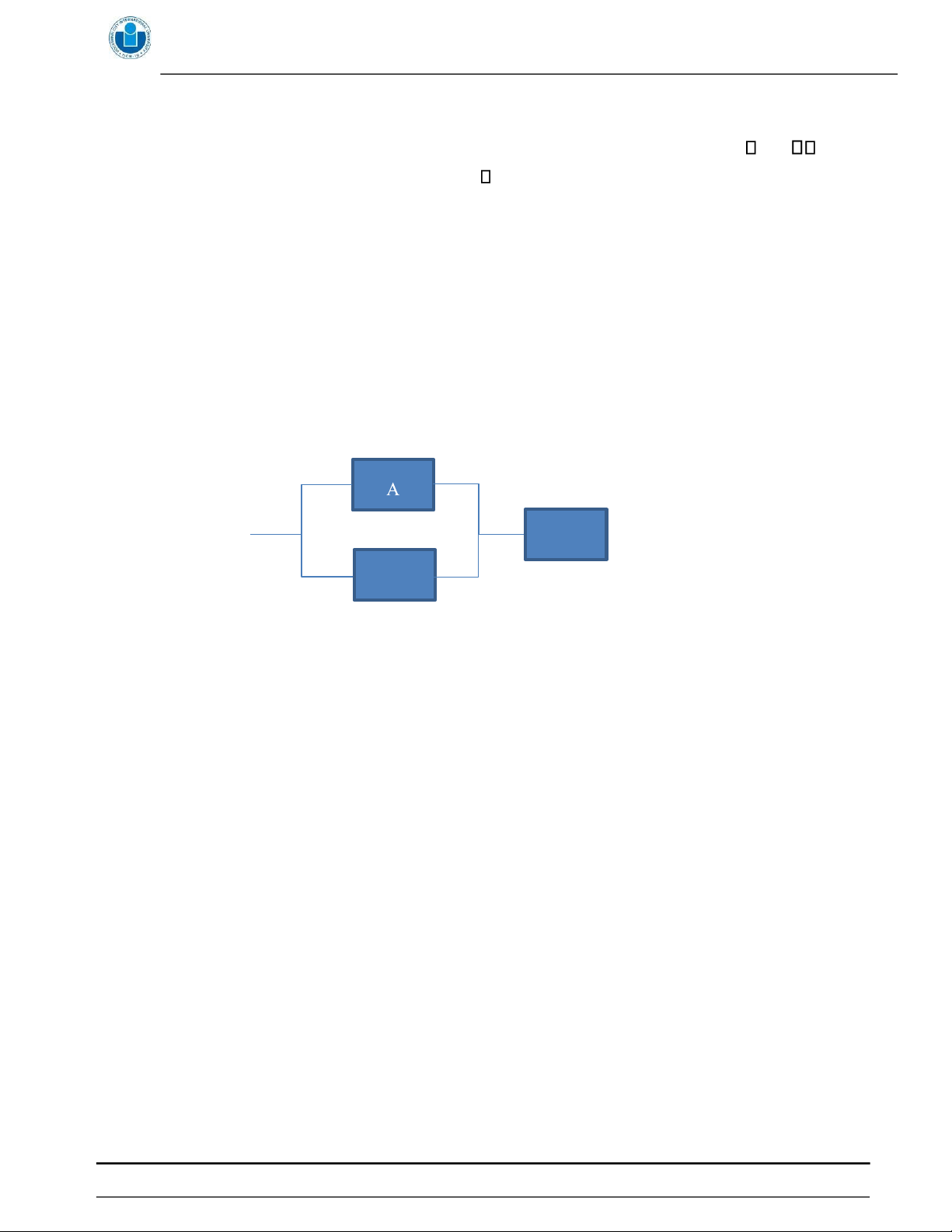
4. Given a system constructed as below: C B
These kind of system works in a logic like this:
- If they are put in series: for example X14X2, the system fails when any of its component fails
- If they are put in parallel: for example A and B in the above picture, the system fails only when both of the components fail
Component A’s working time before failure is known to follow exponential distribution with mean = 5 hours
Component B’s working time before failure is known to follow exponential distribution with mean = 8 hours
Component C’s working time before failure is known to follow exponential distribution with mean = 6 hours
a. What is the probability that the system will fail before 10 hours
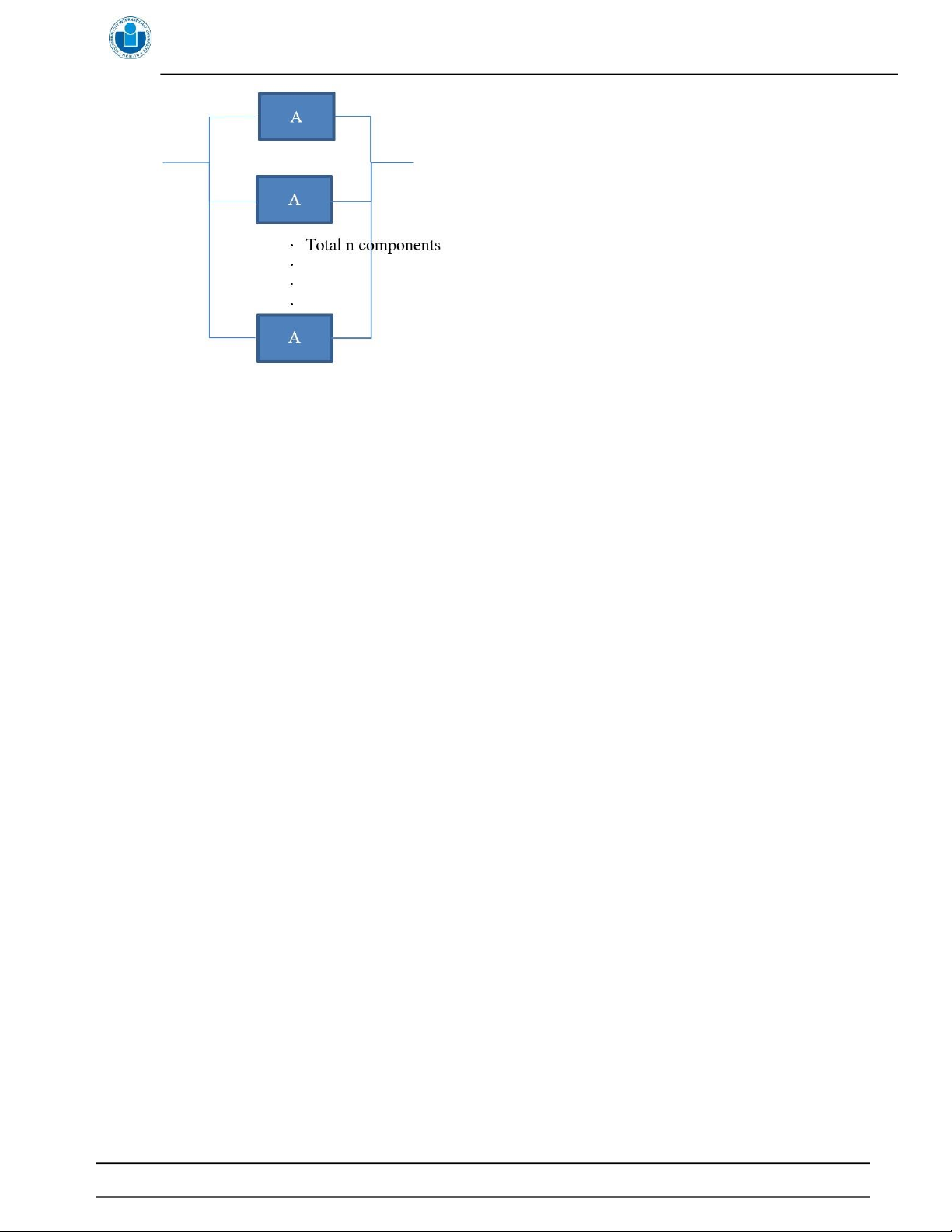
b. The engineers have change the system into k-out-of-n:
Engineering Probability and Statistics – Midterm Exam
THE INTERNATIONAL UNIVERSITY (IU) Course: Engineering Probability and Statistics
Department of Industrial and Systems Engineering
The system works in the sense that it needs at least k numbers of components to work in
order for the system to work normally. If n-k number of components fail then the system will fail.
Given that n = 10 and k = 3, each component’s working time before failure is known to
follow exponential distribution with mean = 5 hours. Find the probability that the system
operates normally after 8 hours of working.
5. A coin is tossed five times. For the 1st time that the head appears the player will be rewarded one.
For the 2nd time that the Head appears the total reward will be added 2. For the 3rd time that the
Head appears the total reward will be added 3. The same rule is applied for the 4th and 5th
appearance of the head. Given that the probability of Head appearance is 0.4
a. Find the expected reward that the player received.
b. Find the variance of this reward. 6.
Nicotine amount inside a cigarette is believed to follow Normal distribution with mean 12mg and variance 2mg.
a. What is the probability that nicotine amount in 1 cigarette is between 11.42mg and 14.75mg
b. A normal pack of cigarette has 20 cigarettes inside. What is the probability that nicotine
amount of a pack exceed 243mg?
c. A cigarette is classified as 1.89 standard deviation from the mean. Otherwise it will be If the cigarette company performs the quality test for 1200 cigarettes. How many cigarettes will be classified as
Engineering Probability and Statistics – Midterm Exam
THE INTERNATIONAL UNIVERSITY (IU) Course: Engineering Probability and Statistics
Department of Industrial and Systems Engineering
PLEASE SHOW YOUR WORK! GOOD LUCK
Engineering Probability and Statistics – Midterm Exam