
BE KIEM TRA CIlIA HQC K! II— NAM HQC 2020
— 2021
MON TOAN HOC
—
KilO! 12
ThOi gian lam bài
:
60 phñt
8 câu, 07 diem; môi culu 0,25 diem)
MADE 121
(
TRUUN
NANG
X1IEU,TDTT
Phãn I. TRACth.
Li
sO
GIAO DIJC VA DAO TO TP
HO
CHI MINI-I
TRU'O'NG THPT NANG KHIEU TDTT H.BC
E
CHINH THU'C
Câu 1:
Cho mt cAu (S) có phirang trInh (S): (x —
3)2 + (y — 1)
2
+ (z + 2)
2
= 9.
Tça d tam
I
cUa
(S) là:
A.
1(3,1,2)
B.
1(3, —1,2)
C.
1(-3, —1,2)
D.
1(3,1, —2)
Câu 2: Mt nguyen ham cüa ham s
f(x)
eX
— 3
là:
A.
F(x) =
e
x
B.
F(
x
)=
e
x_3
C.
F(
x
)=
e
x_3
x
D.
F(
x
)=3
x
_
e
x
Câu 3
: Cho mt phng
(P)
qua
A(1, —2,0)
và cO vectci pháp tuyn i = (
5,3,1).
Phuiimg trInh cUa (P)
là:
A. 5(x
-1)+3(y-2)+z=0
B.
5(x-1)+3(y-2)+oz=0
C. 5(x
-1)+3(y+2)+z=0
D.
5(x-1)+3(y+2)+0z=0
Cãu
4:
Trong không gian vO'i h tnic t9a d
Oxyz,
cho hai diem
A(2,0, —3), B(4,2,
—1). Toa d
trung dim
I
cüa
AB là:
A.
/(3,1,
—2)
B. 1(-1, —1, —1)
C. 1(1,1,1)
D.
1(3,
Câu
5: Giá trj cüa tIch phân
I =
dx là:
A.2
B.4
C.6
D.8
Cãu 6:
Cho
j1
f(x)dx = —2
và i:
f(x)dx = 5.
Giá tn cña tIch phân J
f(x)dx
là:
A.1
B.4
C.2
D.3
Câu
7: Cho
I f(x
2
+ i) .2xdx.
Khi di bin bang cách dt
t
=
x
2
+
1 thi I tr thành:
A.
f
B.
f
C. ft4dt
D.
f
Câu 8:
Cho hinh phng
(H):
(C):y = f(x)
Ox
x=a
x=b
v&i
a <
b.
Cong thirc tInh din tIch cUa
(H)
là:
A.
B.
=
=
1/4 Ma d 121

C.
s=
dx
D.
S=ff(x)dx
Câu 9:
Cho
f(x)
và
g(x)
là các ham s lien tuc, có nguyen ham trên [a,bJ. Phát biu nào sau dày
dung:
A. f{f(x).g(x)]dx
=
ff(x)dxjg(x)dx
ff(x)dx ~
0
flf(x)Idx
=
b
b
b
f
[f(x) +
g(x)Jdx
=
f
f(x)dx
+
f
a
a
a
Cãu 10:
Ktquãcña
1
=
j'i
xdx
là:
x
2
-1
A.
J=
.
InIx
2
_1J+c
B. I=_.lnIx2_1I+C
C. I=Inlx
2-
1I+C
D. J=ln(x
2
-1)+C
Câu 11: Cho ham
s
F(x)
là mt nguyen ham
cüa
ham s
f(x)
=
2x
+
1
và
F(1)
=
6. Khi dO:
A.
F(x)=x
2
+x-4
B.
F(x)=x
2
—x-4
C.
F(x)=x
2
—x+4
D.
F(x)=x
2
+x+4
Câu 12:
Cho mt cu (S) CO phuang trinh (S): x
2
+ y
2
+
z
2
-
4x
-
2y + 4z
=
0. Ban kInh cña (S)
là:
A. R=1
B. R=2
C. R=3
D. R=4
Câu 13: Cho
jdx
=
2,
vOi
m
làsthirc1ânho'n 1. Giátri ct1am là:
A. e
B.
3e
C.
2e
D. 4e
Cãu 14: KtquãciaJ
=
f
x
.
e
xd
x
la
:
A.
J=
e
x.(
x
+1)+C
B.
C.
J=2
e
x
.
(
x
_1)+C
D. J__2
e
x.(
x
i1)+C
CIu 15: Trong không gian vài h triic tpa d
Oxyz,
cho vecto
=
(3,0,
—m)
vuông góc vOi
vectcY
=
(1,4, —6), vOi
m
là tham s
thixc.
Giá tn cüa
m
là:
B.
C.
D.
A.
1
2
B.2
C.
1
2
D.-2
Cãu 16:
Cho mt phng
(P): x
+
2y
-
2z +
16
=
0 Va diem
A(1,1,
—1). Khoâng cách tir
A
dn
(P)
2/4Mãdê 121

là:
A.
3
9
B.
C.7
D.21
Câu 17: Cho
f f(x)dx = 2x
3
- 5x
2
+ x + C.
Bitt
F(x)
là nguyen
ham
cüa
f(x)
trên IL Khi do
F(1) - F(-1) b.ng:
A.
-10.
B.
8.
C. 6.
D.
2.
Câu 18:
Trong không gian
Oxyz,
tim bit vuông góc vci hai vecto
d
= (1;
3; 4), = (-1; 2; 3).
A.
= (
1; 7;
-5).
B. ê
(1; 7;
5).
C.
= (
2; -14; 10).
D.
= (-
3; 21; 15).
Câu 19:
Cho bitt
f
1
dx = !ln
+ C.
Mênh d nào sau day di'ing?
x
2
-7x+6 a x-1
D.
2b-a=:3
A.
2a-b=3.
B. b
-a=1.
C. a-b=l.
Câu 20: Giâ sr mt vt di tr trng thai nghi
t 0(s)
chuyn dng th.ng vâi vn té,c v(t) =
t(5 - t)(m/s).
TIm quang di.rang vt di duçic cho dn khi no drng 1i.
A.
(m).
B. --
(m).
C.
(m).
D.
(in).
Câu 21: Trong không gian
Oxyz,
cho dim
M(8; -2; 4). Goi A,
B ln hrçt là hinh chiu cüa
M
trên
các trc
Ox, Oz.
Phrcmg trInh mt ph&ng di qua ba dim
M, A
và
B
là
A.
8x+32y-16z+60=0.
B.
x+4y+2z-80.
C.
x+4y+2z-12=0.
D.
8x+32y+16z+60=0.
Câu22: Timf
1
dx
cos
4
x
A.
tanx + tan
3
x + C.
B.
2 tan x - 3 tan
3
x + C.
C.
tanx+3tan
3
x+C.
D.
tanx+!tan
3
x+C.
Câu 23: Cho ham
f(x)
xác djnh và lien tic trên IL Tim
m
d thoâ
f
3
10
f(x)dx
-
fmf(
x
)d
x
f
5
10
f(x)dx
A.
m = 4.
B.
m = .
C. m = .
D.
m = 5.
Cu 24:
Trong không gian vOi h t9a d
Oxyz,
cho dim
M(1; -2; 3).
Gçi
I
là hinh chiu vuông góc
cüa
M
trên
(Oxy).
Phiro'ng trinh nào duài day là phuang trInh mt cAu tam
I
và qua
M?
A.
(xfl
2
+(y+2)
2
+z
2
=I.
B. (x
-1)
2
+(y+2)
2
+z
2
9.
C. (x-
1)2
+ (y- 2)
2
+z
2
= 9.
D. (x-
1)2
+ (y+
2)
2
+z
2
= 3.
Cu 25:
Trong khOng gian vOi h t9a d
Oxyz,
cho bn dim
A(0;
0; 2), 5(3; 0; 5),
C(1;
1; 0),
D(4; 1; 2). D
dài duâng cao cUa tü din
ABCD
ht tir dinh
D
xu6ng mt phng
(ABC)
là:
A. 11.
B.
.
C. 1.
D. /ii.
Câu26:
Chohamsf(x) > 0vâ1m9ix> -1,f(0)= lvaf(x) = Vx+ 1.f'(x)vrimQix> -1.
3/4Mãdê 121
Mnh d nào duâi day dUng?
A.
f(3) <2
B.
4 <f(3) <6
C.
2 <f(3) <4
D. f(3) > 6
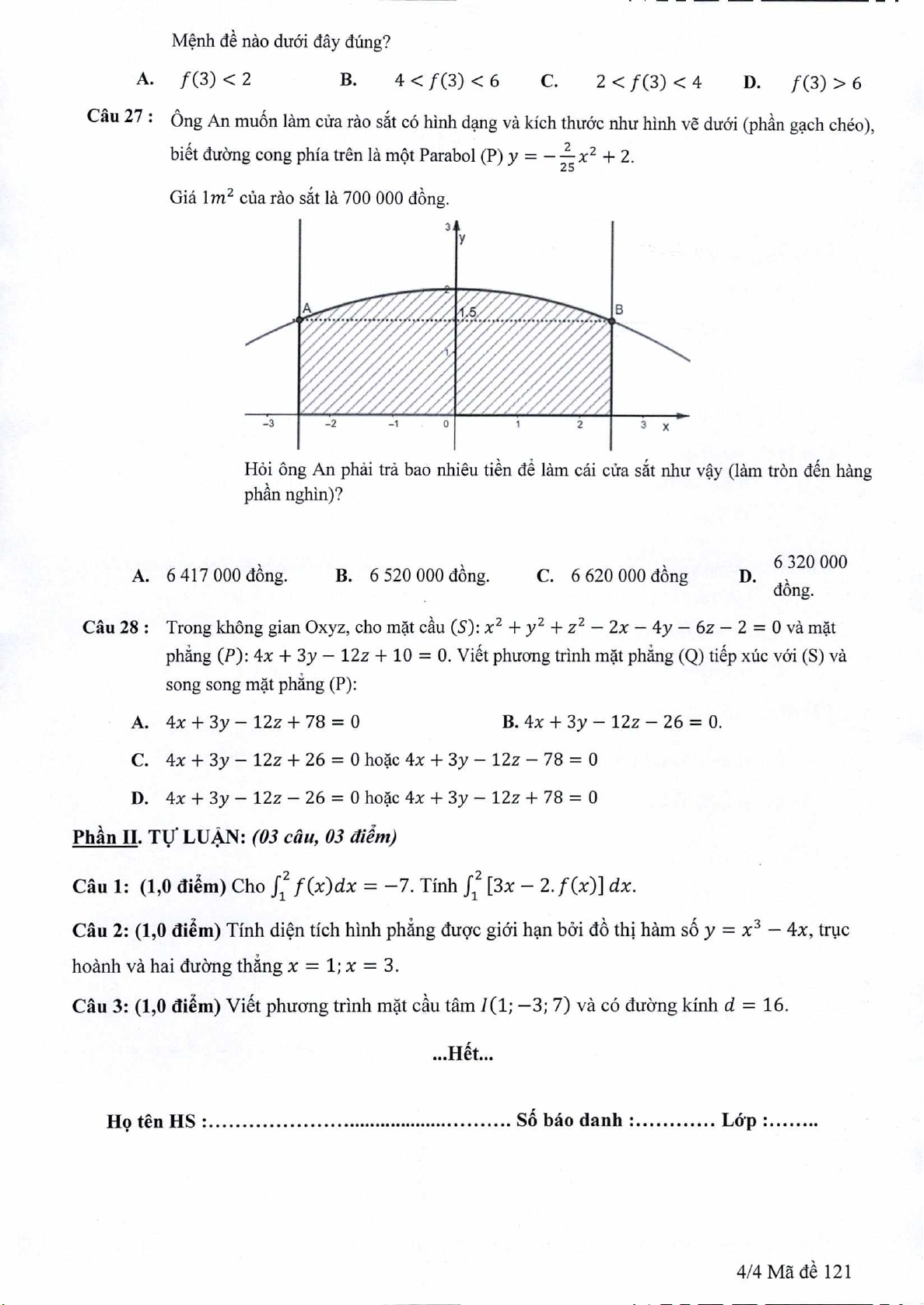
Câu 27: Ong An mun lam cira rào st cO hinh
dang
và kIch thiiàc nhu hinh v duvi (jhAn gach chéo),
bitt duàng cong phIa trén là mt Parabol (P) y = —
x2 +
2.
Giá
1rn
2
cUa rào st là 700 000 dng.
HOi ông An phãi trá bao nhiêu tin d lam cái cira st nhtr vy (lam trôn dn hang
phn nghin)?
A.
6417000dng.
B. 6520000dng.
C. 6620000dng
D. 6320000
dong.
Câu 28: Trong không gian Oxyz, cho mt cAu (S):
x
2
+ y
2
+
z
2
— 2x — —
6z
— 2 = 0 và mat
phng
(P): 4x +
3y — 12z + 10 = 0. Vit phucmg trInh mt ph.ng
(Q)
tip xUc vâi (S) va
song song mt phng (P):
A. 4x+3y-12z+78=0
B.4x+3y-12z-26=0.
C.
4x+3y-12z+26=0hoc4x+3y-12z-78=0
D.
4x+3y-12z-26=0hoc4x+3y-12z+78=0
Phn II. TU LUN:
(03 câu, 03
diem)
Câu 1: (1,0 dim)
Cho
ff(x)dx = —7.
TInh
f [3x — 2.f(x)] dx.
Câu
2:
(1,0 dim)
Tinh din tIch hinh phng duçc giâi
han
bi d thj ham s y =
x
3
-
4x,
tric
hoành và hai dixng th.ng x = 1;
x = 3.
Câu 3: (1,0 dim)
Vi& phircing trInh rnt cAu tarn
1(1; —3;
7) và có dithng kInh
d
= 16.
...Ht...
Ho ten HS
S báo danh
L&p
4/4Mäd 121

SC GIAO DI,JC VA DAO TiO TP HO CHI MINH
TRUONG THPT NANG KHIEU TDTT H.BC
DE CHINH THU'C
TRNG
- TBLJNC HC Pt1 fliQ
\ANG KHIEU TOTT
,\J18iNH CHAMIj/
--
PhiIn I. TRAC NGIIiM:
(28 culu, 07 a?êm; môi culu 0,25
diem)
Câu 1:
Mt nguyen ham cüa ham s
f(x) =
e
x — 3
là:
A.
F(
x
)=
e
x_3
B.
F(x) =
e
x
C.
F(
x
)=3
x
_
e
x
D.
F(
x
)=
e
x_3
x
Cãu
2: Cho mat c.0 (S) có phiing trInh (S): (x —
3)2 + (y — 1)
2
+ (z + 2)
2
=
9. Ta d tam
/ cüa (S) là:
A.
/(-3, —1,2)
B.
1(3,1, —2)
C. 1(3,1,2)
D. 1(3, —1,2)
Cãu 3:
Cho
I
=
j'(x
2
+ i) .2xclx.
Khi di bin btng cách dat
t = x
2
+ 1
thi I tr thành:
A.
f3t
4
dt
B.
ft
4
dt
.
D.
ft
4
dt
Câu 4: Cho
f31
f(x)dx = —2
và
f f(x)dx = 5.
Giá trj cüa tfch phân j
f(x)dx
là:
A.3
B.2
C.1
D.4
Câu 5:
Trong không giari viii h tric t9a d
Oxyz,
cho hai dim
A(2,0, —3), B(4,2, —1).
Tpa do
trung diem
I
cua
AB
la.
(9.!
R6 HU
\\
NAG
KU
A.
1(3,0, —2)
B. /(1,1,1)
C.
1(3,1, —2)
D.
I(-1,
—1,—i)
B1NH
Câu 6:
Cho
mat
phâng
(P)
qua
A(1, —2,0)
và
CO
vecta pháp tuyn ff = (
5,3,1).
Phuong trInh cüa
(P) là:
A.
5(x-1)+3(y+2)+z=0
B. 5(x
-1)+3(y-2)+Oz=0
C.
5(x-1)+3(y-2)+z=0
D.
5(x-1)+3(y+2)+oz=0
Câu
7: Giátrj cüatIch phân / =
fdx là:
A.8
11.2
C.6
D.4
Cãu8:
((C):y=f(x)
Cho hInh phng
(H): ° a
, vâi a
<b.
COng thirc tInh din tIch cia
(H) là:
x=b
A.
S=ff(x)dx
B.S=
C.
S=flf(x)(dx
D.
S=ff(x)dx
1/4 Ma d 122
TRA GIU'A HQC Kill
— NAM
HQC
2020 —2021
MON TOAN HQC
—
KHOI 12
Thôi gian lam bai
:
60 phüt
MA
BE 122

Câu 9: Cho rntt
cu
(S) Co phrong trInh (S): x
2
+ y
2
+ z
2
-
4x
-
2
y +
4z
=
0. Ban kinh cOa (S)
là:
A. R=1
B.
R=2
C.
R=4
D. R=3
Cãu 10: Cho m.t phâng
(P): x + 2y
-
2z +
16
=
0 và dim A(1,1, —1).
Khoãng
cách trA dn (P)
là:
A.7
B.aZ
c.z
9
3
D.
21
Câu 11: Cho
f(x)
và g(x) là các ham s lien tic, Co nguyen ham trén {a,b]. Phát biu nào sau day
dung:
A.
flfx)Idx
=
B.
I
dx ~
0
C.
f
[f(x) + g(x)]dx
=
f
f(x)dx + fg(x)dx
D.
f
{f(x).9(x)]dx
=
ff(x)dx.fg(x)dx
Cãu 12: Cho ham s6
F(x)
là mt nguyen ham cüa ham s6
f(x)
=
2x + 1 vã
F(1)
=
6. Khi do:
A.
F(x)=x
2
+x-4
B.
F(x)=x
2
+x+4
C.
F(x)=x
2
—x+4
D.
F(x)=x
2
—x-4
Câu 13: KtquacuaJ
=
5
x.edx
là:
A.J=2e(x1)+C
B.J=e.(x1)+C
C.J=
e
x.
x
+1)+C
D.J=2
e
x.(
x
+1)+C
Cãu 14: Trong không gian vài h tric t9a d
Oxyz,
cho vectcx a
=
(3,0,
—m)
vuOng
góc
vOi
vectci
=
(1,4, —6), vth
m
là tham s6 th%rc. Giá trj cüa m là:
B.-2
c.-J
D.2
2
2
Câu15: Ketquacual=f4-xdx1à:
A. J=lnx
2
-1I+C
B. I=ln(x
2
—i)+C
C.
1
1.I
n
I
x
2_1I+C
D.
J=_.lIlx2_1I+C
Câu 16:
Cho
f
m
dx
=
2, vâimlàs thrclànhan 1. Giátri cUamlàlà:
1x
A. e
B. 3e
C. 4e
D.
2e
2/4 Ma d 122

Câu 17:
Cho bitt
f
1
dx = 1n
+ C.
Mênh d nào sau day diing?
x
2
-7x+6 a x-1
A.
a—b1.
B.
b—a=1.
C.
2a—b3.
D.
2b
—a=3
Câu 18:
Cho ham
f(x)
xác dinh và lien tuc trén ll. Tim md thoà
f
3
10
f(x)dx
-
fmf(
x
)d
x
=
f51°
f(x)dx
A. m=4.
B. m=.
C. m=5.
D. m=.
Câu 19:
Trong không gian
Oxyz,
cho dim
M(8;
—2;
4).
Goi
A,
B lAn 1uçt là hinh chiu cüa
M
trêfl
cac
trtic
Ox, Oz.
Phuang trinh mtt phng di qua ba dim
M, A
và
B
là
A. x+4y+2z-8=0.
B. 8x+32y+16z+60=0.
C. x+4y+2z-12=0.
D. 8x+32y-16z+60=0.
Câu 20:
Trong không gian
Oxyz,
tim bit vuông góc vOi hai vecta = (1; 3; 4),
b
(-1; 2; 3).
A.
L = (1; 7; —5).
B. ' = (2;
—14; 10).
C.
= (-3;
21;
15).
D.
= (1; 7; 5).
Câu 21:
Cho
f f(x)dx = 2x
3
—
5x
2
+ x +
C.
Biêt
F(x)
là nguyen ham cüa f(x) trên ll.. Khi dO
F(1) — F(-1)
bang:
A. —10.
B. 2.
C. 8.
D. 6.
Cãu 22: Trong không gian vOi he tpa d
Oxyz,
cho diem
M(1;
—2; 3). Gçi
I
là hiiih chiCu vuOnggc
Ti1
k
cüa
M
hen
(Oxy).
Phwmg trinh nao duâi day là phi.rcng trinh m.t cAu tam
I
và qua
M?T
A.
(x-1)
2
+(y+2)
2
+z
2
=9.
B.
(x-1)
2
+(y-2)
2
+z
2
=9.
HQUNC
UTDTT
C. (x — 1)
2
+
(y
+
2)2
+ z
2
= 3.
D. (x —
1)2 +
(y +
2)2
+ z
2
=
\
1.
HA
CIu 23:
Giã sr môt vt di tir trng thai nghi
t = U(s)
chuyn dng thang vâi vn tc
v(t)
=
t(5 —
t)(m/s).
Tim quãng duOng vt di duc cho dn khi no dung
lai.
A.
(m).
B.
(m).
C.
(m).
D.
(m).
Câu24:
Tirnj
1
dx
cos
4
x
A.
tanx +
3
tan
3
x + C.
B. 2
tan x —
3
tan
3
x + C.
C.
tanx + ! tan
3
x + C.
D.
tanx + ! tan
3
x + C.
Câu 25:
Trong không gian vO h tça d
Oxyz,
cho bn dim
A(0;
0; 2),
B(3; 0; 5), C(1; 1; 0),
D(4; 1;
2). Do dài dumg cao cüa ttr din
ABCD
h tn dinh
D
xung mt phang
ABC là
A. 11.
B.
C.
1.
D.
JH.
Câu 26:
Trong không gian Oxyz, cho mat cAu (S): x
2
+ y
2
+
z
2
— 2x — 4.y —
6z — 2 = 0
và
mt
phtng
(P): 4x + 3y — 12z + 10 = 0.
Vit phuang trInh mt phang
(Q)
tip
xiic vái (S) và
song song m.t phtng (P):
A. 4x+3y—
12z-26=
0hoc4x+3y-12z+78= 0
3/4Màdê 122
B.
4x+3y-12z+78=0.
C.
4x+3y-12z+26=0hoac4x+3y-12z-78=O
D.
4x+3y-12z-26=0.
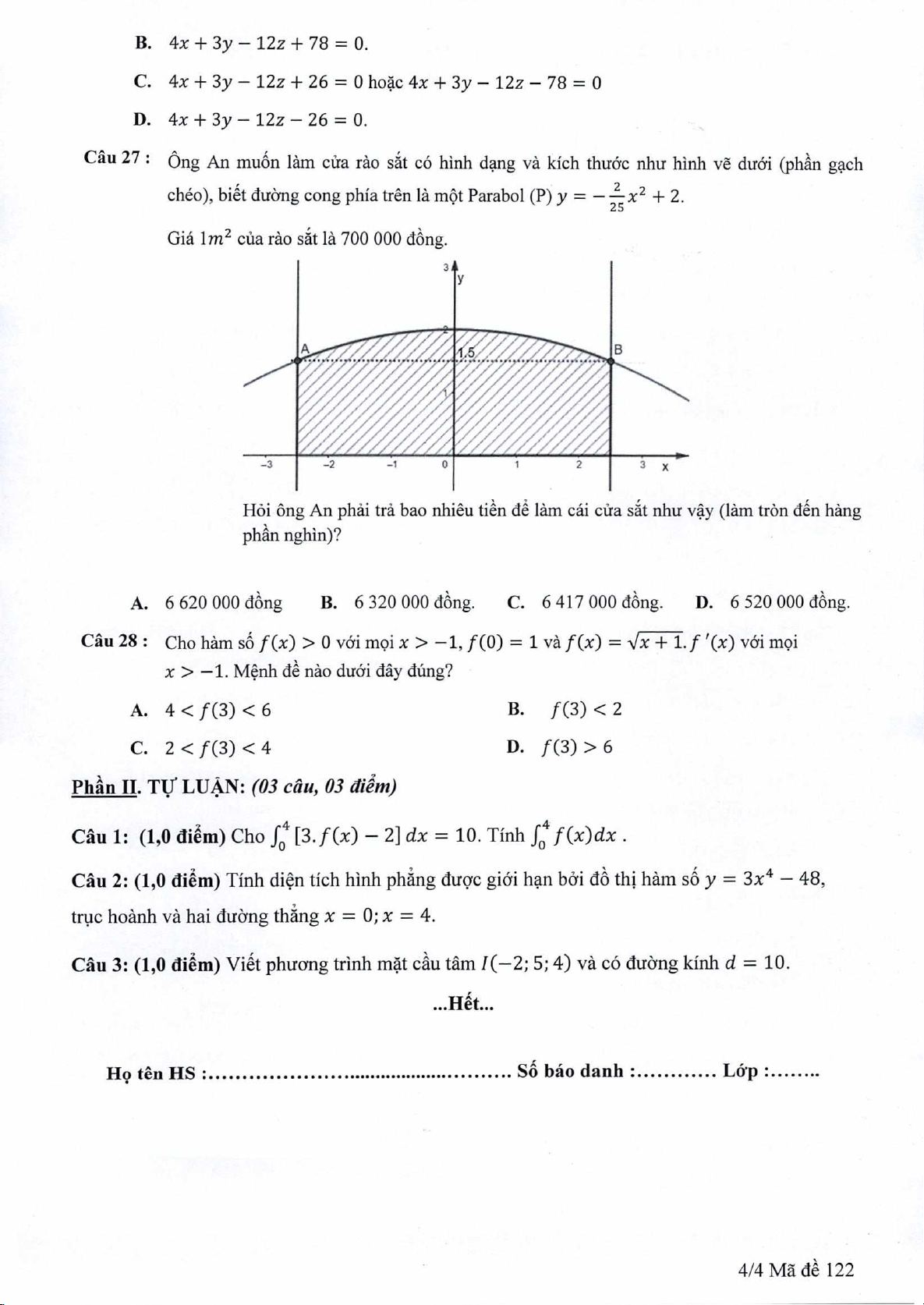
Câu 27: Ong An mun
lam
cüa rào st có hinh dng và kIch thi.rOc nlnr hInh
ye
di.râi (phn gch
chéo), bitt dixing cong phia trên là
mOt
Parabol (P) y = —
x2 +
2.
Giã
1m
2
cüa rào st là 700 000 dng.
HOi ông An phái trà bao nhiêu tin d
lam
cái cira st nhu vy (lam trôn dn hang
ph.n nghIn)?
A. 6620000dng
B. 6320000dng. C. 6417000dng. D. 6520000dng.
Câu 28: Cho ham
sf(x)
>0 vOi moi x > —1, f(0) = 1 vàf(x) =
Vx +
1.f '(x) vOi moi
x> —1. Mnh d nào dixâi day dung?
A. 4<f(3)<6
B. f(3)<2
C. 2 <f(3) <4
D. f(3) > 6
Phân
II.
TV LUAN:
(03 câu, 03 dkm)
Cãu 1: (1,0 dim)
Cho
j
[3.f(x) — 2] dx = 10.
TInh
ff(x)dx.
Câu 2: (1,0 diem)
TInh din tIch hinh phng disçic giOi
h?n
bi d thj ham
s y = 3x
4
— 48,
trlic hoành và hai dung thng x = 0; x = 4.
Cãu 3: (1,0 dim)
Vit phucing trInh mt cu tam
I(-2; 5;
4) và có duàng kInh
d
= 10.
...Hét...
H9 ten HS
S báo danh
Lo'p
4/4Md 122

TRA
GIUA
HOC Kill
— NAM HOC 2020 — 2021
1/
MON TOAN HQC
—
KHOI 12
'iHCPHlFtlUXi
Thoi gian
lam
bãi
:
60 phut
;'
XfflEU TUTT
. Bfl
Phân I. TRAC NJL
(28 câu, 07
diem;
môi câu 0,25 diCm)
MA
BE 123
SO GIAO DIJC VA DAO TiO TP
HO
CHI MINH
TRUONG THPT NANG KHIEU TDTT H.BC
E
CHINH THIXC
Câu 1: Cho mit phng
(P)
qua
A(l, —2,0)
và có vecto pháp tuyn ff = (5,3,1). Plurong trinh cüa
(P)
là:
A. 5(x
-1)+3(y-2)+0z0
B. 5(x-1)+3(y+2)+OzO
C. 5(x
-1)+3(y-2)+z=0
D. 5(x
-1)+3(y+2)+zO
Câu 2: Cho
I
=
f(x
2
+ i).
2xdx.
Khi di bin bang cách dt
t = x
2
+ 1
thI
1
tth thành:
A.
f3t
4
dt
B.
ft
4
dt
C. f2t
4
dt
D. Jt
4
dt
Câu 3:
Trong không gian vi h triic t9a d
Oxyz,
cho hai dim
A(2,0, —3), B(4,2, —1).
T9a d9
trung diem
i
cüa
AB
là:
A.
1(3,0, —2)
B.
1(1,1,1)
C.
1(3,1, —2)
D.
i(-1, —1,—i)
Câu 4:
Cho mtt c.0 (S) có phucrng tririh (S): (x —
3)2 + (y — 1)
2
+ (z + 2)
2
= 9.
Tça d tarn
1
cüa
(5)
là:
A.
1(-3, —1,2)
B.
1(3,1,2)
C. 1(3, —1,2)
D.
1(3,1, —2)
Câu 5:
Mt nguyen ham cüa ham s
f(x) =
e
X — 3
là:
A.
F(x) =
e
x — 3
B.
F(x) =
e
x
C.
F(x) = 3x —
e
x
D.
F(x) = e' —
3x
Cau 6:
Giá
trj
cüa tIch phân
I =
dx
là:
A.8
B.2
C.6
D.4
Can
7: Cho
j3
f(x)dx = —2
và
f36
f(x)dx =
5. Giá trj cüa tich phân
f61
f(x)dx
là:
A.2
B.3
C.1
D.4
.
1ju
'-
hJ
KUEU 1
•
..
9)ICKA
.9
.
-
*
Cãu 8:
(C):y = f(x)
Ox
x=a
x=b
b
Cho hInh ph.ng
(H):
vii
a < b.
Cong thi.rc tInh din tIch cüa
(H)
là:
A.
S=ff(x)dx
B.
S=ff(x)dx
c.
s=
ff(x)dx
D.
S=Jlf(x)Idx
1/4 Ma dê 123

Câu 9:
Trong khong gian vâi h tryc toa d
Oxyz,
cho vecto d
=
(3,0,
—m)
vuông góc vi
vectcY
=
(1,4, —6), vói
m
là tham s thuc. Giá tn cüa
in
là:
A.
--
B. —2
C.
-
D. 2
2
2
Câu 10: Cho
f1m.?dx
=
2, vi
m
là s thrc 1&i hn 1. Giá
trj
cüa
in
là là:
A.
2e
B. e
C. 4e
D.
3e
Câu 11:
Cho mt phng
(P): x + 2y
-
2z
+ 16
=
0
và dim A(1,1, —1). Khoãng cách
tr
A
den
(P)
là:
17
17
A.—
B.7
C.—
D.21
9
3
Câu 12: Cho mt cu (S) có phucmg trInh (S): x
2
+ y
2
+
z
2
-
4x
-
2y +
4z
=
0. Ban kInh cüa
(S) là:
A. R=3
B. R=1
C. R=2
D. R=4
Câu 13:
Kêt qua cña
I
=
xdx
là:
A. I=lnlx
2
-1I+C
B.
l=ln(x
2
-1)+C
C.
j
l
ll2ll+C
1).
1
1
11211+C
Câu 14:
Cho
f(x)
và
g(x)
là các ham s lien tiic
vâ có nguyen ham trên [a,b]. Phát biu nào sau
day dung:
f
[f(x) + g(x)]dx b
b fg(x)dx
J
[f(x). g(x)]dx
=
f
f(x)dx.
f
C.
f
f(x)dx ~
0
flfx)Idx
=
D.
Câu
15:
Cho
ham s
F(x)
là mt nguyen ham cüa ham so f(x)
=
2x + 1 và F(1)
=
6. Khi do:
A. F(x)=x
2
±x+4
B.
P(x)x
2
—x-4
C.
P(x)=x
2
+x-4
D.
F(x)=x
2
—x+4
Câu 16:
Kt qua cUaJ
=
fx.
e
xd
x
là:
A.
J__
e
x(
x
_1)+C
B.
J=2
e
x(
x
_1)+C
C.
J=
e
x(
x
+1)+C
D.
J=2
e
x(
x
+1)+C
2/4 Ma d 123

Câu 17:
Cho ham f(x) xác dinh và lien tuc trên
ll&
Tim m d thoà f310
f(x)dx
-
fm
f(x)dx =
f
10
f(x)dx
A. m=5.
B. m=4.
C.
m=.
D. m=.
Câu 18:
Giã sü mt v.t di tr trng thai nghi t
0(s)
chuyn dng thing vOi vn tc
v(t)
=
t(5 —
t)(m/s).
Tim quäng duing vt di duc cho dn khi no drng 1i.
A.
(m).
B.
(m).
C.
(m).
D.
(m).
Câu 19:
Cho
f f(x)dx
= 2x
3
— 5x
2
+ x +
C.
Bitt F(x) là nguyen ham cüa f(x) trén ll.. Khi do
F(1) — F(-1)
bang:
A.
Cãu 20:
A.
Câu 21: Trong không gian
Oxyz,
tim bit vuông goc vOi hai vecta
i
= (1; 3; 4),
(-1; 2; 3).
A.
= (2; —14; 10).
B.
= (1; 7; 5).
C.
= (-3; 21; 15).
D.
ê
= (1; 7; —5).
Câu22:
Timf
1
dx
cos
4
x
A.
tanx+3tan
3
x+C.
B.
2tanx-3tan
3
x+C.
C.
. -i-
r
D.
-I- tan
3
y -- C
DII
Câu 23: Trong không gian
Oxyz,
cho diem
M(8;
—2; 4). Gi
A,
B lan luot là hInh chiêu cüa
M
trê
các true
Ox, Oz.
Phung trinh mt phâng di qua ba dim
M, A
và
B
là
A. 8x+32y-16z+60=0.
B. x+4y+2z-8=0.
C.
8x+32y+16z+60=0.
D. x+4y+2z-12=0.
Câu 24:
Trong không gian vâi h tça d
Oxyz,
cho dim
M(1;
—2; 3). Gi
I
là hinh chiu vuông
gOc cüa
M
trên
(Oxy).
Phuong trinh nào duâi day là phucing trinh mt cAu tam i và qua M?
A. (x-1)
2
+(y+2)
2
+z
2
=9.
B.
(x-1)
2
+(y-2)
2
+z
2
=9.
C.
(x-1)
2
+(y+2)
2
+z
2
=3.
D. (
x
_1)
2
+(y+2)
2
+
z
2
=Vl
Câu 25: Trong khOng gian Oxyz, cho mt c.0 (S): x
2
+ y
2
+
z
2
— 2x — —
6z
— 2 0 và mt
phâng
(P): 4x + 3y
— 12z + 10 = 0. Vi& phuong trInh mt phng
(Q)
tip xuc vâi (S) và
song song rnt ph.ng (P):
A.
4x+3y-12z-26=0.
B.
4x+3y-12z+26=0hoc4x+3y-12z-78=0
C.
4x+3y-12z-26=0hoc4x+3y-12z+78=0
D.
4x+3y-12z+78=0.
3/4Màdé 123
—10.
B.
1
dx
8.
in
a
C.
6.
+ C.
Mênh dê nào sau dày dung?
D.
2.
Cho bitt
5
=
x
2
-7x+6
x-1
a—b=1.
B.
b—a=1.
C.
2b—a=3
D.
2a—b=3.
CIu 26: Trong không gian
vâi h t9a
do
Oxyz,
cho b6n dMm
A(0;
0; 2), 8(3; 0; 5), C(1;
1; 0),
D(4;
1; 2). D dài thring cao cUa
tr
din
ABCD
h
tCr dinh
D
xu6ng mt ph&ng
ABC
là
A. 11.
B.
/TT.
C. ~.
D. 1.
Cãu27: Chohàmsf(x) >0 vâimçix> —1. f(0)
=
1 vaf(x)
=
\/x
+
1.f '(x) vái rnoi
x> —1. Mn1i d nào duói day dung?
A. 4<f(3)<6 B. f(3)<2
C.
2<f(3)<4 D. f(3)>6
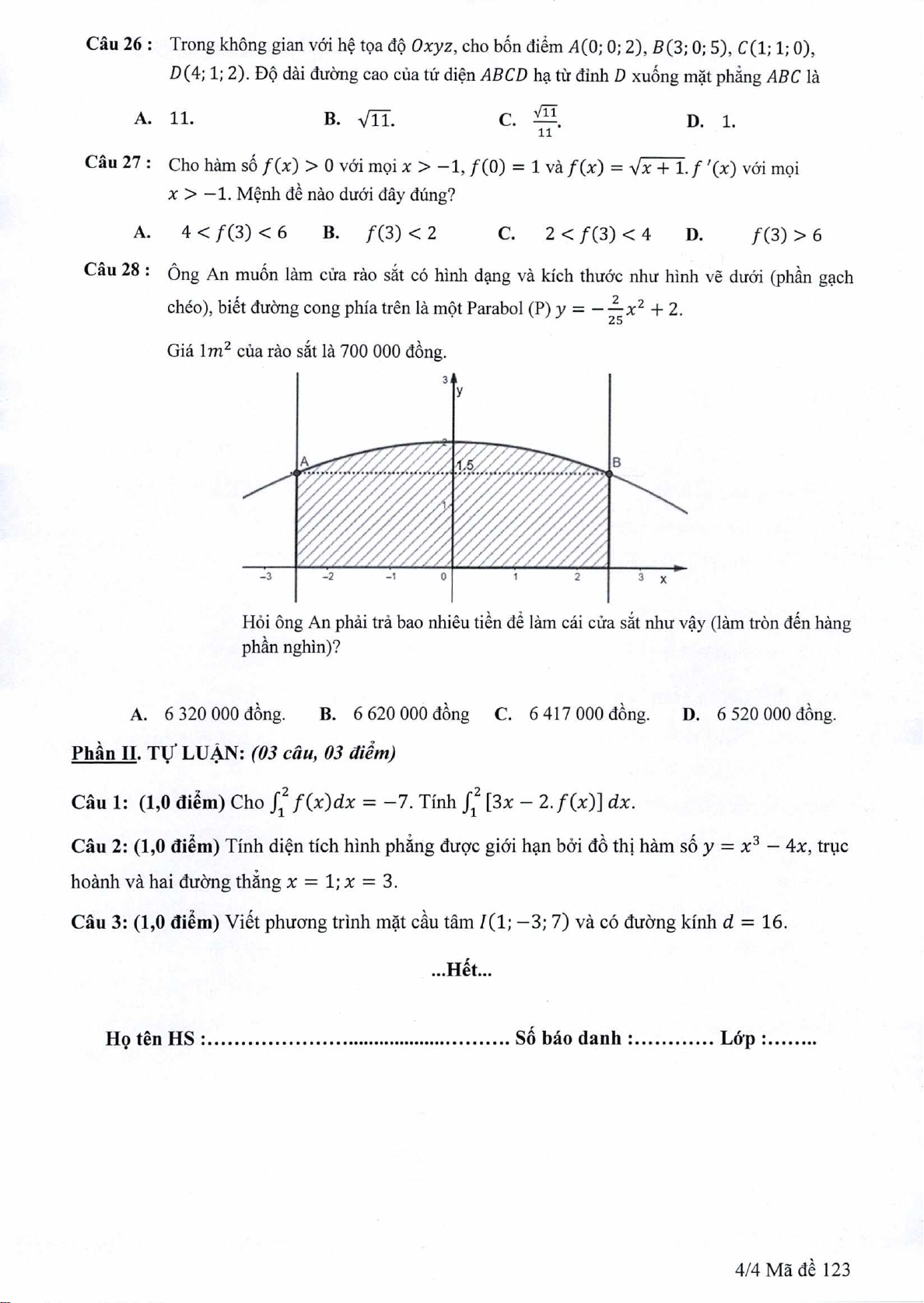
Cãu 28: Ong An mu6n lam ci'ra rào s& có hInh dng và kIch thtràc thu hInh
ye
duài (phân gch
chéo), bit duing cong phia trên là mt Parabol (P) y
=
-
x
2
+ 2.
Giá 1m
2
cUa rào st là 700 000 dng.
HOi ông An phãi trá bao nhiêu tin d lam cái cüa st nhi.r
v.y (lam trôn dn hang
phn nghln)?
A. 6320000dng.
B. 6620000dông C. 6417 000 dông.
D. 6520000dng.
Phn II. TV LU4N:
(03 cat,, 03 diêm,
Câu 1: (1,0 dim) Cho
f
1
2
f(x)dx
=
—7. TInh
f
[3x
-
2.f(x)]
dx.
Can 2: (1,0 dim) TInh din tich hInh
phng duçic giâi hn bi
d thj ham S6
y
=
x
3
-
4x,
triic
hoànhvàhaidtthngth&ngx
=
1;x
=
3.
Câu 3: (1,0 dim) Vit phung trInh mt ctu tam
1(1;
—3; 7) và
Co
dung kinh
d
=
16.
...Hêt...
Ho ten HS
s6
bão danh
Ló'p
4/4 M dé 123

F(x)
= 3x —
B.
F(x)
=
e
x
F(x)
=
e
x — 3
D.
F(x)=e"3x
Cho
f
3
1
f(x)dx
= —
2 va
f
3
6
f(x)dx
= 5. GiatrjcüatIchphânf
6
1
f(x)dxla:
2
B.4
C.1
D.3
Cho mtt cu (S) có phi.rcing trinh (S): (x — 3)2 + (y — 1)
2
+
(z
+
2)2
9. Tça d thin
I
cia (S) là:
I(3,1,-2)
B. 1(3,1,2)
((C):y
=
f(x)
phng
(H):) Ox
x=a
A.
C.
Câu 6:
A.
Câu
7:
A.
Cãu 8:
C.
I(-3,
—1,2)
D.
1(3,
—1,2)
vài a
<
b.
Cong thirc tInh din tIch cüa
(H)
là:
sO GIAO
DVC
VA DAO TO TP HO cHi MINH
TRISYNG THPT
NANG xulEu TDTT H.BC
E CHINH
I
rO
..,I/TRL.rnNG
TRIJNC Ill Phi THO6
HANG KHEU TDTT
\H. BHH CHAMII
Phân I. TR
EM TRA GIIYA HQC 1(111- NAM HQC 2020 - 2021
MON TOAN HQC
—
KilO! 12
Thôi gian
lam
bài: 60 phüt
M:
(28 câu, 07 aiim;
môi câu 0,25
diem)
MA BE 124
Cãu 1:
91
Giá tn cüa tIch phãn
1
=
f
—
dx
là:
A.
8
B.2
C.4
D.6
Cilu 2:
Trong không gian
vài h
triic tça d
Oxyz,
cho hai dirn
A(2,0,
—3),
B(4,2,
—1).
Tha
d
trung dim
I
ci'ia
AB
là:
A.
I(3,1,-2)
B.
1(1,1,1)
C.
I(-1,
—1,—i)
D. 1(3,0, —2)
Câu 3:
Cho mt phng
(P)
qua
A(1,
—2,0)
và có
vectci pháp tuyn ii = (5,3,1). PhuGng trInh cüa
(P)
là:
A.
5(x-1)+3(y+2)+z=0
B. 5(x-1)+3(y-2)+Oz=O
C.
5(x-1)+3(y-2)+z=0
D. 5(x-1)+3(y+2)+Oz=0
Cãu 4: Cho
I
=
f(x
2
+
i).
2xdx. Kbi d6i bin b.ng cách dt t
=
x
2
+ 1 thI I trâ thành:
A.
f3t
4
dt
B.
ft
4
dt
C.
D.
Jt
4
dt
Câu 5:
Mt nguyen ham
cUa ham
s6 f(x) = e'
—
3 là:
ri
/
c
-7
TRLN
'TR1JN6 H3C PHI
k\\ HANG
KHIEI
"<,
BINH CH
x=b
A. S=ff(x)dx
B.
S=Jf(x)dx
C.
S
f
f(x)dx
D. S=Jlf(x)Idx
1/4Màd
124

Câu 9: Cho
fdx
=
2,vàimlàs6thuclonhcml. Giátrjcüamlâlà:
A. 2e
B. 3e
C.e
D.4e
Cãu 10:
Cho
f(x)
và
g(x)
là các ham s lien tiic Va có nguyen ham trên [a,b]. Phát biêu nào sau day
dung:
:
f[f(x)
+
g(x)]dx
bb
fg(x)dx
f
[f(x). g(x)]dx
=
f
f(x)dx.
f
a
a
a
C.
=
I
dx ~
0
D.
Câu 11: Cho mt ctu (S) có phucing trInh (S): x
2
H- y
2
+
z
2
-
4x
-
2y +
4z
=
0. BánkInh cüa(S)
là:
A.
R=4
B.
R=3
C. R=2
D.
R=1
Câu 12: Trong không gian vci h
truc
tça
d
Oxyz,
cho vecta a
=
(3,0,
—m)
vuÔng góc vâi
vectci
=
(1,4, —6), vài
m
là tham s6 th%rc. Giá tn cüa
m
là:
A.-2
B. 1
C. 1
D.2
2
2
Câu 13: Cho ham s Fx)là mt nguyen ham cUa ham s6
f(x)
=
2x + 1 Va F(1)
=
6. Khi do:
A.
F(x)=x
2
—x+4
B.
F(x)=x
2
+x+4
C.
F(x)=x
2
—x-4
U. F(x)=x
2
+x-4
Câu 14:
Cho mt ph.ng
(P): x + 2y
-
2z +
16
=
0 Va dim A(1,1, —1). Khoãng cách tir
A
dn
(P)
là:
A.7
B.21
C.
1
3
D.Z
9
Câu 15:
K& qua cuaJ
=
f
x.
exdx
là:
A. J=2
e
x
.
(
x
_1)+C
B.
J=
e
x.(
x
+1)+C
C.
J=
e
x.(
x
_1)+C
D.
J=2
e
x.(
x
+1)+C
Câul6: Ktquacual=f-
xdxlà:
A.
I=lnjx
2
-1I+C
B.
I=ln(x
2
-1)+C
C.
J
=
i.1
n
1
x
2_1I+C
D.
1
1
112
1
,
+C
2/4 Ma dê 124

Câu 17:
Trong không gian
Oxyz,
cho dim
M(8; -2; 4).
Goi
A,
B ln luçit là hinh chiêu cüa
M
trên
cac triic
Ox, Oz.
Phi.wng trInh mt ph.ng di qua ba diem
M, A
và
B
là
A. x+4y+2z-8=0.
B. 8x+32y-16z+600.
C. 8x+32y+16z+600.
D. x+4y+2z-120.
Câu 18: Trong không gian vái h t9a do
Oxyz,
cho dim
M(1;
-2; 3). Gçi
I
là hInh chiu vuông góc
cüa
M
trên
(Oxy).
Phlrang trinh nào dtrài day là phixcing trinh mt cu tam i và qua M?
A. (x-1)
2
+(y-2)
2
+z
2
=9.
B. (x-1)
2
+(y+2)
2
+z
2
=9.
C. (x-1)
2
+(y+2)
2
+z
2
=3.
D. (
x
_1)
2
+(y+2)
2
+
z
2
=V.
Câu 19:
Giã si mt vt di ttr trtng thai nghi t =
0(s)
chuyn dng thng vài vn tc
v(t)
=
t(5 -
t)(m/s).
TIm quäng thrng vt di drnc cho dn khi no dirng 1i.
125
!(m)
C.
-(m).
D.
1:5
A.
-(m).
B.
12
Câu2O:
Timf
1
dx
cos
4
x
A.
tanx+3tan
3
x+C.
B.
tanx+tanx+C.
C.
2
tan x
- 3
tan
3
x + C.
D.
tanx + tan
3
x + C.
1
1
Ix-bl
Câu 21: Cho bitt
f
dx
= -
In
I
-I + C.
Mênh dé nào sau day diing?
x
2
-7x+6 a ix-il
A. a-b=1.
B. b-a=1.
C.
2b-a=3
D. 2a-b=3.
Câu 22: Cho
5 f(x)dx =
2x
3
-
5x
2
+ x + C.
Bi& F(x) là nguyen ham cüa f(x) trên 1W. Klrii dO
F(1) - F(-l)
b.ng:
fl1OG
A. m =5.
B. m
=4.
C.
m = .
D. m =
Câu 24: Trong không gian
Oxyz,
tim bitt vuOng góc vi hai vectcx = (1; 3; 4), = (-1; 2; 3).
A.
C.
Câu 25: Cho hàms6f(x) >0 vYim9ix>
-1,f(0) = 1
vaf(x)
= Vx +
1.f'(x)vOimçi
x>
-1. Mnh d nào di.râi day dñng?
A.
[(3)
<2
B. 2 <[(3) <4
C.
[(3) > 6
D. 4 <f(3) <6
Câu 26: Ong An mun lam cüa rào s.t có hInh
dang
và kIch thi.xâc nhii hinh
ye
dui (phn gch
chéo), biM di.thng cong phIa trên là mt Parabol (P) y = -
x
2
+ 2.
Giá 1m
2
cüa rào
sAt
là 700 000 dng.
3/4Mãdê 124
TDTT
A. -10.
B. 6.
C. 2.
D. 8.
Câu 23: Cho ham f(x) xác dinh và lien tue trên 1W. Tim m d thoã
f'
°
f(x)dx - 5m
1(x)dx
=
55'° f(x)dx
= (-3; 21;
15).
B.
=
(1;
7;
-5).
E = (
2; -14;
10).
D.
=
(1;
7;
5).

0
3
x
3
y
Hôi ông An phãi trá bao nhiêu tin d lam cái cira st nhu
4y
(lam trôn dn hang
phn nghin)?
A. 6520000dng.
B. 6320000dong.
C. 6620 000 dng
D. 6417000dng.
Câu 27: Trong khong gian vài h tça d
Oxyz,
cho b6n dim
A(O;
0; 2),
8(3; 0; 5), C(1; 1; 0),
D(4;
1; 2). E dài duäng cao cüa ttr din
ABCD
htr dinh
D
xu6ng mat phng
ABC
là
A. 11.
B. 1.
C.
vTT.
D.
Cãu28: TrongkhonggianOxyz,chomtcu(S):x
2
+y
2
+z
2
-2x
-4y
-6z-2 =Ovàmät
ph.ng
(P):
4x + 3y —
12z
+ 10 = 0. Vi& phtrang trinh mt phng
(Q)
tip xüc vci (S)
và
song song mt phng (P):
A.
4x+3y-12z-26 = ohoac4x+3y-12z+78=0
B.
4x+3y-12z-26=0.
C.
4x+3y
-12z+26=0hoãc4x+3y-12z-78=0
D.
4x+3y
-12z+78=0.
Phn II. TIT LUN:
(03 câu, 03 dilm)
Câu 1: (1,0 dim)
Cho
f
[3.
f(x)
— 2]
dx
= 10. TInh
ff(x)dx.
Câu
2:
(1,0 dim) Tinh
din tIch hInh phng duc giii hn bâi d thj ham s y = 3x
4
— 48, triic
hoânh và hai duing thâng x = 0; x =
4.
Can
3: (1,0 dim)
Vi& phuorng trinh mt cu tam I(-2; 5; 4) và
có duing kInh
d
= 10.
...Het...
Hç ten HS
So bão danh
Lóp
4/4 M d 124
-3
sO GIAO
DIJC
VA DAO TAO TP. HCM
TR1I0TG
THPT NANG KHIEU TDTT H.BC
E CHiNH THIYC
Ti,'
/
oAp AN BE KIEM TRA GICA HOC K H
,/
TRLNG
THIJNC HOC PHO
MON: TOAN 12 - NAM HQC: 2020 — 2021
KHIEUTDTT
'\INHc
Phan I. TRAGN11I M
(4 ma de, moi de 28 cau; mm cau 0,25 them
Câu
121
122
123
124
1
D
D
D
C
2
C
B
B
A
3
C
D
C
A
4
A
A
D
B
5
B
C
D
D
6
D
A
D
D
7
B
D
B
A
8
D
C
D
D
9
D
D
A
C
10
A
A
B
A
11
D
C
B
B
12
C
B
A
C
13
A
B
C
B
14
B
C
A
A
15
A
C
A
C
16
C
A
A
C
17
C
B
D
A
18
C
B
B
B
19
B
A
C
D
20
A
B
B
B
21
B
D
A
B
22
A
A
C
B
23
C
D
B
D
24
B
C
A
C
25
B
B
C
C
26
D
A
C
D
27
A
C
D
D
28
D D
C
A
1/5 Dap an
?

Phn II. TJJ LUAN (4
ma de, mó1 de 3 câu; moi cáu 1,0 dim,)
Ma d 121
Câu
Dãp an
Diem
Cho
ff(x)dx
=
—7.
Tinh
f
[3x
—
2.f(x)] dx.
2
2 2
— 2.f(x)J dx = j
3xdx
— j 2.f(x)dx
1
(1,0 diem)
/
=
I
3xdx — 2.
f
f(x)dx
j1
0,25d
0,25 d
9
=-2.(-7)
0,25d
37
0,25d
2
TInh diên tich hInh phãng thrçrc giói h3n bói do thj ham
s y =
x
3
-
4x, truc hoành
và hai thrOng thäng x
=
1; x
=
3.
x
3
— 4x = 0
x = 0(L); x = 2(N); x = —2(L)
0,25 d
2
(1,0 dim)
S
=
flx
3
—
4
xldx
+
f1x
3
—
4
xldx
0,5 d
9
25
17
0,25d
Vit
phuo'ng trInh mit cu tam
1(1; —3;
7)
vA có du'Ong kInh
d
=
16
+ Tam
1(1; —3; 7).
0,25 ci
+Bán kInh
R
=
= 8.
0,25
ci
(1,0 dim)
+Phucng trinh:
(x
—
a)
2
+ (y — b)
2
+ (z — c)
2
= R
2
0,25 ci
(x—
1)2
+(y+3)
2
+(z-7)
2
= 8
2
0,25d
2/5
Dáp
an

Mãd 122
Câu
Dáp an
Diem
Cho
f[3.f(x) —2] dx
=
10. Tinh
ff(x)dx.
4
4
4
f
[3.f(x)_2]dx=l04f3.fx)dx_f2dx=10
0,25d
1
.
dx — 8 = 10
0,25 d
(1,0
diem)
3.
I
f(x)dx = 18
0,25 d
J
o
f(x)dx = 6
0,25 d
J
o
TInh din tIch hmnh phng duçc giói hn bi d thj ham
s y =
3x
4
—
48, truc hoành
và
hal dirô'ng thing x
=
0; x
=
4.
3x
4
—48 = 0
x = 2(N);x = —2(L)
0,25 d
2
s=f
2
13x
4
_
4
81dx+f
4
I
3
x
4-48
1dx
(1,0 diem)
2
0,5 d
384
2496
=—+
=576
5
5
0,25d
Vit phirong trInh mt cu tam
I(-2; 5;
4) vã có duong kInh
d
=
10.
+Tâml(
-2;5;4).
0,25 d
+J3ánkinhR==5.
0,25d
(1,0 dim)
2
+Phucng trInh: (x —
a)
2
+ (y — b)
2
+ (z
—
c)
2
= R
2
0,25 d
(x+2)
2
+(y-5)
2
+(z-4)
2
5
2
0,25d
çO
T
TRIIØN U
ic ic
Puö'TI
HG KHIEU TI
H. BINH CRAM
3/5
Dap
an

Ma d
123
Cãu
Dáp
an
Diem
Cho
ff (x)dx
=
—
7. Tinh
f
[3x
—
2.f(x)]
dx.
2
— 2. f(x)] dx
=
f
3xdx
-
f
2. f(x)dx
0,25d
=f
3xdx_2.f f(x)dx
0,25d
.x
(1,0 diem)
1
1
=-2.(-7)
O,25d
37
O,25d
TInh din tIch hInh phang throc gioi hn b&i d thi ham
s6 y =
x
3
—
4x, trizc
và hai throng thàng
x
= 1; x = 3.
hoành
x
3
— 4x = 0
x
0(L);x = 2(N);x = —2(L)
0,25 d
2
2
3
S=
I
Ix
3
-4xldx+
I
x
3
-4xdx
(1,0 diem)
0,5 d
9
2517
=
.
:+
-
:i:
-
_
----
0,25d
Vit phirong trInh mt cu tam
1(1;
—3; 7) Va có du*ng kInh
d
=
16
+Tâml(1;
-3;7).
0,25 d
+Bãn kInh
R
=
= 8.
0,25 d
(1,0 dim)
+Phtrong trInh:
(x
—
a)
2
+ (
y —
b)
2
+ (z
—
c)
2
= R
2
0,25 d
0,25d
4/5
Dáp an

Mãd124
Câu
Dáp an
Diem
Cho f[3.f(x) —2]
dx
=
10. Tinh
ff(x)dx.
[3. f(x) — 2] dx = 10
L4
f(x)dx
-
f2dx = 10
0,25d
3
.
ff(
x
)d
x
_8
=10
0,25d
(1,0 diem)
0
3.f
f(x)dx = 18
0,25 d
0
'
.4
J
f(x)dx = 6
0,25 d
0
TInh din tIch hlnh phng throc giói hn bôi d th ham s
y = 3x
4
—
48, tryc
và
hal throng thng
x = 0; x =
4.
hoành
3x
4
-48=O
x= 2(N);x= —2(L)
0,25d
2
S=
I
3x4-481dx+
I
I3x
4
-481dx
(1,0 diem)
J
2
0,5 d
384
2496
=—+
=576
5
5
Vit phuong trinh mt cu tam
I(-2;
5; 4) và có du*ng kinh
d
=
10.
+ Tam
I(-2; 5; 4).
0,25 d
+BánkinhR==5.
0,25d
(1,0 dim)
2
+Phixang trInh: (x — a)
2
+ (y — b)
2
+ (z — c)
2
= R
2
0 25 d
(x+2)
2
+(y-5)
2
+(z-4)
2
=5
2
0
:
25d
TP H C/il Minh, ngày 08 tháng 3 nàrn 2021
Duyt cüa Ban Giám Hiu
P.Hiu trirO'ng Chuyên mon
To tru&ng chuyên mon
Trân Thj Huyn Trang
Nyi nhân:
+ BGH;
+ GV trong to;
+Luuh, siCM.
Cao Minh Thang
5/5
Dap an
Bấm Tải xuống để xem toàn bộ.
Preview text:
Document Outline
- Page 1
- Page 2
- Page 3
- Page 4
- Page 5
- Page 6
- Page 7
- Page 8
- Page 9
- Page 10
- Page 11
- Page 12
- Page 13
- Page 14
- Page 15
- Page 16
- Page 17
- Page 18
- Page 19
- Page 20
- Page 21




