Đề thi HK1 Toán 9 năm 2018 – 2019 phòng GD&ĐT Thị Xã Phú Mỹ – Bà Rịa – Vũng Tàu

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề tham khảo kiểm tra cuối học kì 1 môn Toán 9 năm học 2018 – 2019. Mời bạn đọc đón xem.

18 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 9

Môn: Toán 9

Thông tin:

4 trang 9 tháng trước

Tác giả:

Profile Hà Việt Anh
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
THỊ XÃ PHÚ MỸ
ĐỀ CHÍNH THỨC
HƯỚNG DẪN CHẤM ĐỀ CHÍNH THỨC
KIỂM TRA HỌC KỲ I NĂM HỌC 2018-2019
MÔN: TOÁN LỚP 9
(Hướng dẫn chấm có 03 trang)
Bài 1 (2,5 điểm).
1. Thực hiện phép tính:
a)
3
64 125
+ −
b)
2 2 18 2 8
+ −
2. Rút gọn biểu thức
3 1
2 1
3 1
a a a
P
a a
+ −
= − ⋅ +
+ −
với
0; 1
a a
≥ ≠
.
Bài 2 (3,0 điểm).
Trong m
ặ
t ph
ẳ
ng t
ọ
a
độ
cho hai
đườ
ng th
ẳ
ng
1
( ) : 2 2
d y x
= +
và
2
1
( ) : 2
2
d y x
= − −
. G
ọ
i
C
là giao
đ
i
ể
m c
ủ
a
1
( )
d
,
2
( )
d
. Hai
đườ
ng th
ẳ
ng
1
( )
d
và
2
( )
d
c
ắ
t
tr
ụ
c
Oy
theo th
ứ
t
ự
t
ạ
i
D
và
E
.
a) V
ẽ
1
( )
d
và
2
( )
d
trên cùng m
ặ
t ph
ẳ
ng t
ọ
a
độ
.
b) Tìm t
ọ
a
độ
các
đ
i
ể
m
, , .
C D E
c) Tính di
ệ
n tích tam giác
CDE
.
Bài 3 (1,5 điểm).
Cho tam giác
ABC
vuông t
ạ
i
A
có
đườ
ng cao
AH
(
H BC
∈
). Tính
,
AH AC
và
Sin
C
bi
ết
9 ; 16 .
BH cm CH cm
= =
Bài 4 (2,5 điểm).
Cho đường tròn tâm
O
đường kính
AB
và
C
là một điểm trên đường tròn (
C
khác
A
và
B
). Kẻ
CH
vuông góc với
AB
tại
.
H
Gọi
I
là trung điểm của
;
OI
cắt
tiếp tuyến tại
A
của
( )
O
tại
;
M
MB
cắt
CH
tại
.
K
a) Chứng minh:
OI AC
⊥
và tam giác
ABC
vuông tại
.
C
b) Chứng minh
MC
là tiếp tuyến của
( )
O
.
c) Chứng minh
K
là trung điểm của
.
CH
Bài 5 (0,5 điểm).
Giải phương trình:
5 7 2
x x
− + − =
.
_____
Hết
_____
Họ và tên học sinh ................................................. Số báo danh .......................
Ch
ữ ký giáo viên coi kiểm tra ................................
2
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
THỊ XÃ PHÚ MỸ
ĐỀ CHÍNH THỨC
HƯỚNG DẪN CHẤM ĐỀ CHÍNH THỨC
KIỂM TRA HỌC KỲ I NĂM HỌC 2018-2019
MÔN: TOÁN LỚP 9
(Hướng dẫn chấm có 03 trang)
Bài 1 (2,5 điểm).
1. Thực hiện phép tính:
a)
3
64 125
+ −
b)
2 2 18 2 8
+ −
2. Rút gọn biểu thức
3 1
2 1
3 1
a a a
P
a a
+ −
= − ⋅ +
+ −
với
0; 1
a a
≥ ≠
.
Câu Nội dung Điểm
1
(1,5đ)
a)
3
64 125 8 ( 5) 3
+ − = + − =
.
Tính
đượ
c:
64 8
=
(0,25);
3
125 5
− = −
(0,25);
8 ( 5) 3
+ − =
(0,25)
0,75
b)
2 2 18 2 8 2 2 3 2 4 2 2
+ − = + − =
.
Tính được:
18 3 2
=
(0,25);
2 8 4 2
=
(0,25);
2 2 3 2 4 2 2
+ − =
(0,25)
0,75
2
(1,0đ)
Với
0; 1
a a
≥ ≠
ta có:
3 1
2 1
3 1
a a a
P
a a
+ −
= − ⋅ +
+ −
(
)
(
)
(
)
3 1 1
2 . 1
3 1
a a a a
a a
+ − +
= − +
+ −
0,5
(
)
(
)
2 . 1 1
a a
= − + +
0,25
(
)
(
)
2 2 4
a a a
= − + = −
.
0,25
Bài 2 (3,0 điểm).
Trong mặt phẳng tọa độ
cho hai đường thẳng
1
( ) : 2 2
d y x
= +
và
2
1
( ) : 2
2
d y x
= − −
. Gọi
C
là giao điểm của
1
( )
d
,
2
( )
d
. Hai đường thẳng
1
( )
d
và
2
( )
d
cắt
trục
Oy
theo thứ tự tại
D
và
E
.
a) Vẽ
1
( )
d
và
2
( )
d
trên cùng mặt phẳng tọa độ
.
b) Tìm tọa độ các điểm
, , .
C D E
c) Tính di
ện tích tam giác
CDE
.
3
Câu Nội dung Điểm
a
(1,0đ)
Lập bảng giá trị: xác định đúng 2 điểm. 0,5
Vẽ đúng hệ trục tọa độ và đồ thị hàm số. 0,5
b
(1,0đ)
C
là giao điểm của
1
( )
d
,
2
( )
d
nên ta có:
1
2 2 2
2
x x
+ = − −
4 4 4 5 8 1,6
x x x x
⇔ + = − − ⇔ = − ⇔ = −
0,25
Thay
1,6
x
= −
vào
2 2
y x
= +
ta có:
2.( 1,6) 2 1,2
y
= − + = −
Vậy
(
)
1,6; 1,2 .
C
− −
0,25
1
( )
d
cắt trục
Oy
tại
D
nên ta có:
(
)
2.0 2 2 0; 2
y D
= + = ⇒
0,25
2
( )
d
cắt trục
Oy
tại
E
nên ta có:
( )
1
.0 2 2 0; 2
2
y E
= − − = −
⇒
−
0,25
c
(1,0đ)
Gọi
,
H K
lần lượt là hình chiếu của điểm
C
trên
,
Ox Oy
, ta có:
1,6 1,6; 2 2 4
CK OH DE DO OE
= = − = = + = + − =
0,5
Diện tích tam giác
CDE
là:
1 1
. . .4.1,6 3,2
2 2
DE CK = = (
đ
vdt).
0,5
Bài 3 (1,5 điểm).
Cho tam giác
ABC
vuông t
ạ
i
A
có
đườ
ng cao
AH
(
H BC
∈
). Tính
,
AH AC
và
Sin
C
bi
ế
t
9 ; 16 .
BH cm CH cm
= =
Nội dung Điểm
16cm
9cm
H
C
A
B
2
. . 9.16 144 12 .
AH BH CH AH BH CH cm
=
⇒
= = = =
0,5
2
. . 16.(9 16) 16.25 400 20 .
AC CH BC AC CH BC cm
= ⇒ = = + = = =
0,5
12
Sin 0,6
20
AH
C
AC
= = = .
0,5
4
Bài 4 (2,5 điểm). Cho đường tròn tâm
O
đường kính
AB
và
C
là một điểm trên đường
tròn (
C
khác
A
và
B
). Kẻ
CH
vuông góc với
AB
tại
.
H
Gọi
I
là trung điểm của
;
OI
cắt tiếp tuyến tại
A
của
( )
O
tại
;
M
MB
cắt
CH
tại
.
K
a) Chứng minh:
OI AC
⊥
và tam giác
ABC
vuông tại
.
C
b) Chứng minh
MC
là tiếp tuyến của
( )
O
.
c) Chứng minh
K
là trung điểm của
.
CH
Câu Nội dung Điểm
Hình
vẽ
(0,25đ)
K
M
I
H
O
A
B
C
0,25
a
(1,25đ)
I
là trung điểm của dây
AC
(không đi qua tâm)
OI AC
⇒ ⊥
.
0,5
ACB
∆
có đường trung tuyến
CO
bằng một nửa cạnh đối diện
AB
(cùng bán kính) nên vuông tại
C
.
(Hoặc dùng tam giác nội tiếp đường tròn có cạnh là đường kính)
0,75
b
(0,50đ)
AOC
∆
cân tại
O
có
OI
là trung tuyến nên
OI
cũng là phân giác
( . . )
MOA MOC MOA MOC c g c
⇒ = ⇒ ∆ = ∆
0,25
0
90
MCO MAO MC OC MC
⇒ = = ⇒ ⊥ ⇒
là tiếp tuyến của
( )
O
0,25
c
(0,50đ)
MAB
∆
có
//
KH MA
(cùng vuông góc với
AB
)
. . .
2
2.
KH HB AM HB AM HB AM HB
KH KH
AM AB AB AO AO
⇒ = ⇒ = = ⇒ = (1)
0,25
//
CB MO
(cùng vuông góc với
AC
)
MOA CBH
⇒ =
(đồng vị)
.
( . )
MA AO AM HB
MOA CBH g g CH
CH HB AO
⇒ ∆ ∆ ⇒ = ⇒ =∽ (2)
Từ (1), (2) suy ra
2
CH KH K
= ⇒
là trung điểm của
.
CH
0,25
Bài 5 (0,5 điểm). Giải phương trình:
5 7 2
x x
− + − =
.
Nội dung Điểm
5 7 5 7
5 7 2
5 2 ( 5)(7 ) 7 4 2 ( 5)(7 ) 2
x x
x x
x x x x x x
≤ ≤ ≤ ≤
− + − = ⇔ ⇔
− + − − + − = − − =
0,25
2 2
5 7 5 7
5 7
6
( 5)(7 ) 1
12 36 0 ( 6) 0
x x
x
x
x x
x x x
≤ ≤ ≤ ≤
≤ ≤
⇔ ⇔ ⇔ ⇔ =
− − =
− + = − =
.
0,25
* Ghi chú: Nếu học sinh làm cách khác đúng, giáo viên căn cứ vào điểm của từng
phần để chấm cho phù hợp.
_____
Hết
_____
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM ĐỀ CHÍNH THỨC
THỊ XÃ PHÚ MỸ
KIỂM TRA HỌC KỲ I NĂM HỌC 2018-2019
MÔN: TOÁN LỚP 9
ĐỀ CHÍNH THỨC
(Hướng dẫn chấm có 03 trang)
Bài 1 (2,5 điểm). 1. Thực hiện phép tính: a) 3 64 + 1 − 25 b) 2 2 + 18 − 2 8  a 3 a  +  a −1 
2. Rút gọn biểu thức P =  − 2  ⋅ + 
1 với a ≥ 0;a ≠ 1.  a + 3   a −1 
Bài 2 (3,0 điểm).
Trong mặt phẳng tọa độ Oxy cho hai đường thẳng (d ) : y = 2x + 2 và 1 1
(d ) : y = − x − 2 . Gọi C
(d ) , (d ) . Hai đường thẳng (d ) và (d ) 2 là giao điểm của 2 1 2 1 2 cắt
trục Oy theo thứ tự tại D và E .
a) Vẽ (d ) và (d ) trên cùng mặt phẳng tọa độ Oxy . 1 2
b) Tìm tọa độ các điểm C, D, E.
c) Tính diện tích tam giác CDE .
Bài 3 (1,5 điểm).
Cho tam giác ABC vuông tại A có đường cao AH ( H ∈ BC ). Tính AH , AC và
SinC biết BH = 9c ; m CH = 16c . m
Bài 4 (2,5 điểm).
Cho đường tròn tâm O đường kính AB và C là một điểm trên đường tròn ( C
khác A và B ). Kẻ CH vuông góc với AB tại H. Gọi I là trung điểm của AC; OI cắt
tiếp tuyến tại A của (O) tại M ; MB cắt CH tại K.
a) Chứng minh: OI ⊥ AC và tam giác ABC vuông tại C.
b) Chứng minh MC là tiếp tuyến của (O) .
c) Chứng minh K là trung điểm của CH.
Bài 5 (0,5 điểm).
Giải phương trình: x − 5 + 7 − x = 2 .
_____Hết_____
Họ và tên học sinh .................................................
Số báo danh .......................
Chữ ký giáo viên coi kiểm tra ................................
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM ĐỀ CHÍNH THỨC
THỊ XÃ PHÚ MỸ
KIỂM TRA HỌC KỲ I NĂM HỌC 2018-2019
MÔN: TOÁN LỚP 9
ĐỀ CHÍNH THỨC
(Hướng dẫn chấm có 03 trang)
Bài 1 (2,5 điểm). 1. Thực hiện phép tính: a) 3 64 + 1 − 25 b) 2 2 + 18 − 2 8  a 3 a  +  a −1 
2. Rút gọn biểu thức P =  − 2  ⋅ + 
1 với a ≥ 0;a ≠ 1.  a + 3   a −1  Câu Nội dung Điểm a) 3 64 + 1 − 25 = 8 + ( 5 − ) = 3 . 0,75
Tính được: 64 = 8 (0,25); 3 −125 = −5 (0,25); 8 + ( 5 − ) = 3 (0,25) 1
(1,5đ) b) 2 2 + 18 − 2 8 = 2 2 + 3 2 − 4 2 = 2 .
Tính được: 18 = 3 2 (0,25); 2 8 = 4 2 (0,25); 0,75 2 2 + 3 2 − 4 2 = 2 (0,25)
Với a ≥ 0;a ≠ 1 ta có:  a 3 a  +  a −1  P =  − 2  ⋅ +  1  a + 3   a −1  0,5     2 a ( a + 3) ( a − ) 1 ( a + ) 1     (1,0đ) = − 2 . +1  a + 3   a −1     
= ( a − 2).( a +1+ ) 1 0,25
= ( a − 2)( a + 2) = a − 4 . 0,25
Bài 2 (3,0 điểm).
Trong mặt phẳng tọa độ Oxy cho hai đường thẳng (d ) : y = 2x + 2 và 1 1
(d ) : y = − x − 2 . Gọi C
(d ) , (d ) . Hai đường thẳng (d ) và (d ) 2 là giao điểm của 2 1 2 1 2 cắt
trục Oy theo thứ tự tại D và E .
a) Vẽ (d ) và (d ) trên cùng mặt phẳng tọa độ Oxy . 1 2
b) Tìm tọa độ các điểm C, D, E.
c) Tính diện tích tam giác CDE . 2 Câu Nội dung Điểm a
Lập bảng giá trị: xác định đúng 2 điểm. 0,5
(1,0đ) Vẽ đúng hệ trục tọa độ và đồ thị hàm số. 0,5
C là giao điểm của (d ) , (d ) nên ta có: 1 2 1 0,25
2x + 2 = − x − 2 ⇔ 4x + 4 = −x − 4 ⇔ 5x = 8 − ⇔ x = 1 − ,6 2 b Thay x = 1
− ,6 vào y = 2x + 2 ta có: y = 2.( 1 − ,6) + 2 = 1 − , 2 0,25 (1,0 đ) Vậy C ( 1 − ,6; −1, 2).
(d ) cắt trục Oy tại D nên ta có: y = 2.0 + 2 = 2 ⇒ D(0; 2) 0,25 1 1
(d ) cắt trục Oy tại E nên ta có: y = − .0 − 2 = 2 − ⇒ E (0; 2 − ) 0,25 2 2
Gọi H , K lần lượt là hình chiếu của điểm C trên Ox,Oy , ta có: 0,5 c CK = OH = 1
− ,6 = 1,6; DE = DO + OE = 2 + 2 − = 4 (1,0đ) 1 1
Diện tích tam giác CDE là: .DE.CK = .4.1,6 = 3, 2 (đvdt). 0,5 2 2
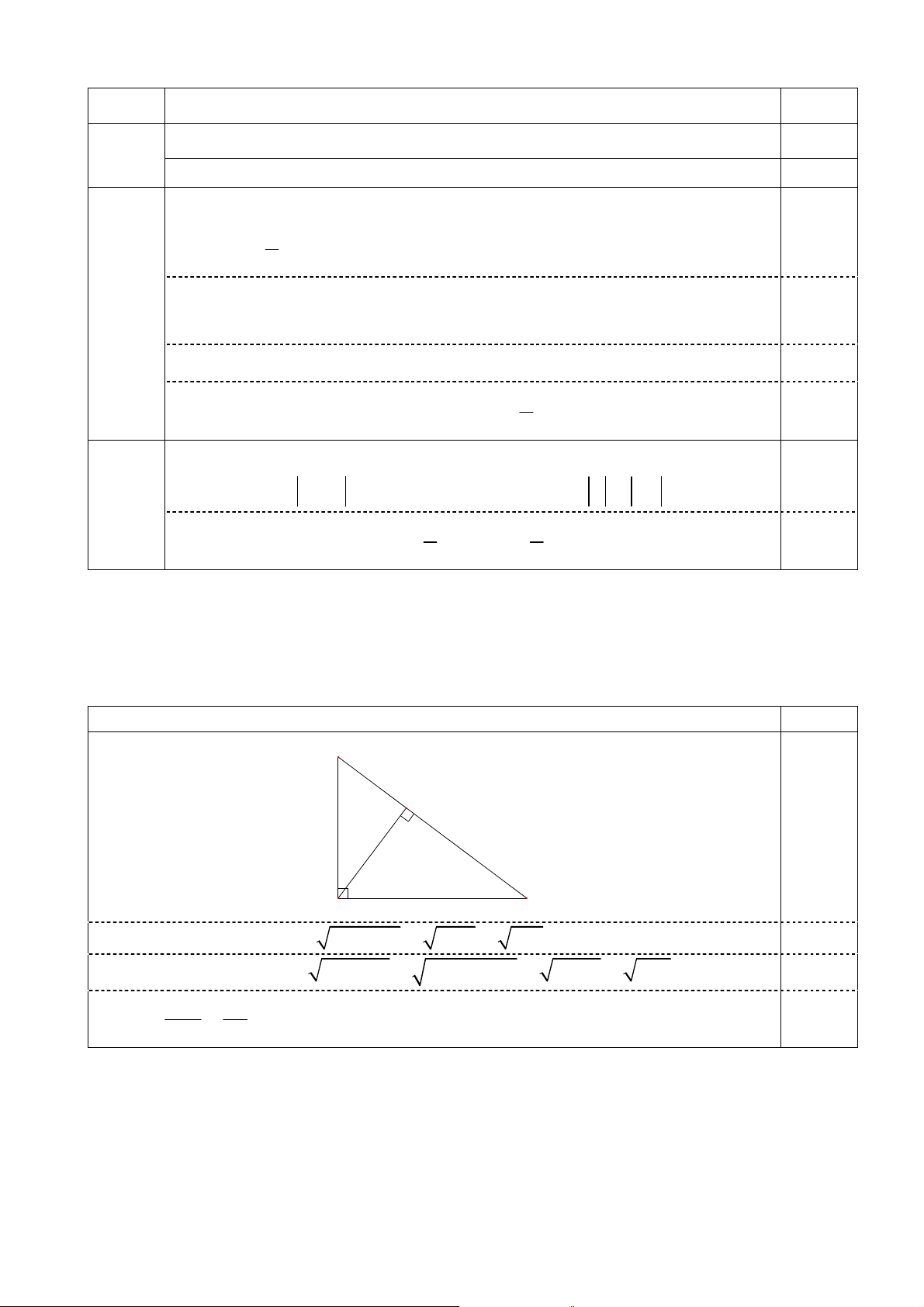
Bài 3 (1,5 điểm).
Cho tam giác ABC vuông tại A có đường cao AH ( H ∈ BC ). Tính AH , AC và
SinC biết BH = 9c ; m CH = 16c . m Nội dung Điểm B 9cm H 16cm C A 2
AH = BH.CH ⇒ AH =
BH.CH = 9.16 = 144 = 12c . m 0,5 2
AC = CH .BC ⇒ AC = CH .BC = 16.(9 + 16) = 16.25 = 400 = 20c . m 0,5 AH 12 SinC = = = 0,6 . 0,5 AC 20 3
Bài 4 (2,5 điểm). Cho đường tròn tâm O đường kính AB và C là một điểm trên đường
tròn (C khác A và B ). Kẻ CH vuông góc với AB tại H. Gọi I là trung điểm của
AC; OI cắt tiếp tuyến tại A của (O) tại M ; MB cắt CH tại K.
a) Chứng minh: OI ⊥ AC và tam giác ABC vuông tại C.
b) Chứng minh MC là tiếp tuyến của (O) .
c) Chứng minh K là trung điểm của CH. Câu Nội dung Điểm M C Hình vẽ I K 0,25 (0,25đ) A B O H
I là trung điểm của dây AC (không đi qua tâm) ⇒ OI ⊥ AC . 0,5 a A
∆ CB có đường trung tuyến CO bằng một nửa cạnh đối diện AB
(1,25đ) (cùng bán kính) nên vuông tại C . 0,75
(Hoặc dùng tam giác nội tiếp đường tròn có cạnh là đường kính) A
∆ OC cân tại O có OI là trung tuyến nên OI cũng là phân giác b ⇒ 0,25 = MOA MOC ⇒ M ∆ OA = M ∆ OC ( . c g.c) (0,50đ) ⇒ = 0 MCO
MAO = 90 ⇒ MC ⊥ OC ⇒ MC là tiếp tuyến của (O) 0,25
∆MAB có KH //MA (cùng vuông góc với AB ) KH HB AM .HB AM .HB AM .HB ⇒ 0,25 = ⇒ KH = = ⇒ 2KH = (1) AM AB AB 2.AO AO c (0,50 ⇒
đ) CB//MO (cùng vuông góc với AC ) = MOA CBH (đồng vị) MA AO AM .HB ⇒ M ∆ OA ∽ C
∆ BH (g.g) ⇒ = ⇒ CH = (2) 0,25 CH HB AO
Từ (1), (2) suy ra CH = 2KH ⇒ K là trung điểm của CH.
Bài 5 (0,5 điểm). Giải phương trình: x − 5 + 7 − x = 2 . Nội dung Điểm 5  ≤ x ≤ 7 5    ≤ x ≤ 7
x − 5 + 7 − x = 2 ⇔  ⇔  0,25
x −5+ 2 (x −5)(7 − ) x + 7 − x = 4 2  (x −5)(7 − ) x = 2 5  ≤ x ≤ 7 5  ≤ x ≤ 7 5  ≤ x ≤ 7 ⇔  ⇔  ⇔  ⇔ x = 6 . 0,25 2 2
(x − 5)(7 − x) = 1
x −12x + 36 = 0 (x − 6) = 0
* Ghi chú: Nếu học sinh làm cách khác đúng, giáo viên căn cứ vào điểm của từng
phần để chấm cho phù hợp.
_____Hết_____ 4