Đề thi HK1 Toán 9 năm học 2018 – 2019 phòng GD&ĐT Đống Đa – Hà Nội

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề tham khảo kiểm tra cuối học kì 1 môn Toán 9 năm học 2018 – 2019. Mời bạn đọc đón xem.

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 9

Môn: Toán 9

Thông tin:

12 trang 7 tháng trước

Tác giả:

Profile Hà Việt Anh
1/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
QUẬN ĐỐNG ĐA
ĐỀ KIỂM TRA HỌC KÌ I
NĂM HỌC 2018 − 2019
MÔN: TOÁN 9
Thời gian làm bài: 90 phút.
Bài 1. (2,0 điểm).
1) Tính giá trị của biểu thức:
( )
2
33
1 3 3 12 1
11
M = − − + +
2) Giải phương trình:
9 9 1 1x x− − = −
Bài 2 (2,0 điểm)
Cho biểu thức
2 1
3
x
A
x
−
=
−
và
2 3 9
9
3
x x x
B
x
x
+ +
= −
−
+
với
0; 9x x≥ ≠
1) Tính giá trị của
A
khi
25x =
2) Rút gọn biểu thức
B
3) Cho
A
P
B
=
. Tìm giá trị nhỏ nhất của
P
Bài 3 (2,0 điểm)
Cho hàm số bậc nhất
( 1) 4 ( ) ( 1)y m x d m= − − ≠
1) Vẽ đồ thị hàm số khi
2m =
2) Tìm
m
để
( )d
song song với đồ thị hàm số
1
3 2 ( )y x d= − +
3) Tìm
m
để
( )d
cắt đồ thị hàm số
2
7 ( )y x d= −
tại một điểm nằm ở bên
trái trục tung.
2/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 4 (3,5 điểm)
Cho đường tròn
( ; )O R
đường kính
AB
. Vẽ tiếp tuyến
Bx
của
( )O
. Trên
cùng 1 nửa mặt phẳng bờ
AB
có chứa
Bx
, lấy điểm
M
thuộc
( )O
(
M
khác
A
và
B
) sao cho
MA MB>
. Tia
AM
cắt
Bx
tại
C
. Từ
C
kẻ tiếp
tuyến thứ hai
CD
với
( )O
(
D
là tiếp điểm)
1) Chứng minh
OC BD⊥
2) Chứng minh bốn điểm
, , ,
O B C D
cùng thuộc một đường tròn
3) Chứng minh
CMD CDA=
4) Kẻ
MH
vuông góc với
AB
tại
H
. Tìm vị trí của
M
để chu vi tam
giác
OMH
đạt giá trị lớn nhất.
Bài 5 (0,5 điểm)
Cho
, ,x y z
là các số dương thay đổi thỏa mãn:
5
xy yz zx+ + =
. Tìm giá
trị nhỏ nhất của biểu thức
2 2 2
3 3T x y z= + +
3/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
HƯỚNG DẪN GIẢI
Bài 1. (2,0 điểm).
1) Tính giá trị của biểu thức:
( )
2
33
1 3 3 12 1
11
M = − − + +
( )
2
33
1 3 3 12 1
11
M = − − + +
33
1 3 3 4.3 1
11
3 1 3.2 3 3 1
3 1 6 3 3 1
4 3
M
M
M
M
= − − + +
= − − + +
= − − + +
= −
2) Giải phương trình:
9 9 1 1x x− − = −
Lời giải
Điều kiện:
9 9 0 9 9
1
1 0 1
x x
x
x x
− ≥ ≥
⇔ ⇔ ≥
− ≥ ≥
9 9 1 1 9( 1) 1 1x x x x− − = − ⇔ − − = −
3 1 1 1x x⇔ − − = −
3 1 1 1x x⇔ − − − =
2 1 1x⇔ − =
4( 1) 1x⇔ − =
5
4 4 1 4 5
4
x x x⇔ − = ⇔ = ⇔ =
(thỏa điều kiện 1x ≥ )
Vậy phương trình có nghiệm duy nhất
5
4
x =
4/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 2 (2,0 điểm)
Cho biểu thức
2 1
3
x
A
x
−
=
−
và
2 3 9
9
3
x x x
B
x
x
+ +
= −
−
+
với
0; 9x x≥ ≠
1) Tính giá trị của A khi 25x =
2) Rút gọn biểu thức B
3) Cho
A
P
B
=
. Tìm giá trị nhỏ nhất của P
Lời giải
1) Với 25x = (thỏa mãn điều kiện), thay vào A, ta có:
2 25 1
25 3
A
−
=
−
2.5 1 10 1 9
5 3 2 2
A
− −
= = =
−
2) Rút gọn biểu thức B
2 3 9
9
3
x x x
B
x
x
+ +
= −
−
+
( )( )
( )
( )( )
. 3
2 3 9
3 3 3 3
x x
x x
B
x x x x
−
+ +
= −
+ − + −
( )( ) ( )( )
2 3 9 3 6 9
3 3 3 3
x x x x x x
B
x x x x
+ + − + + +
= =
+ − + −
( )
( )( )
2
3
3
3
3 3
x
x
B
x
x x
+
+
= =
−
+ −
5/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
3) Tìm giá trị nhỏ nhất của
P
2 1 3
:
3 3
A x x
P
B
x x
− +
= =
− −
2 1 3
3 3
x x
P
x x
− −
= ⋅
− +
( )( )
( )( )
2 1 3
2 1
3
3 3
x x
x
P
x
x x
− −
−
= =
+
− +
( ) ( )
2 3 7 2 3
7 7
2
3 3 3 3
x x
P
x x x x
+ − +
− −
= = + = +
+ + + +
Ta có:
7 7
0 3 3
3
3
x x
x
− −
≥ ⇔ + ≥ ⇒ ≥
+
7 7
2 2
3
3
P
x
− −
⇒ = + ≥ +
+
1
3
P
−
⇒ ≥
Vậy
1
3
MinP = − khi
0x =
6/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 3 (2,0 điểm)
Cho hàm số bậc nhất
( 1) 4 ( ) ( 1)y m x d m= − − ≠
1) Vẽ đồ thị hàm số khi
2m =
2) Tìm
m
để
( )d
song song với đồ thị hàm số
1
3 2 ( )y x d= − +
3) Tìm
m
để
( )d
cắt đồ thị hàm số
2
7 ( )y x d= −
tại một điểm nằm ở bên
trái trục tung.
Lời giải
1) Thay
2m =
, ta được:
4 ( )y x d= −
Đồ thị hàm số
4 ( )y x d= −
là đường thẳng đi qua điểm
(0; 4)−
và điểm
(4;0)
x
y
4
-5
-4
-3
O
2
3
1
-2
-1
-2 -1
3
2
y = x-4
1
7/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
2)
1
1 3
( )//( ) 2
4 2
m
d d m
− = −
⇔ ⇔ = −
− ≠
Vậy
1
( )//( )d d
khi
2m = −
3) Phương trình hoành độ giao điểm của
( )d
và
2
( )d
:
( 1) 4 7m x x− − = −
4 7mx x x⇔ − − = −
7 4mx x x⇔ − − = − +
( 2) 3x m⇔ − = −
3
2
x
m
−
⇔ =
−
( 2)m ≠
Vì giao điểm của
( )d
và
2
( )d
nằm bên trái trục tung nên ta có:
3
0
2
x
m
−
= <
−
2 0m⇔ − >
2m⇔ >
Vậy
2m >
thì
( )d
cắt
2
( )d
tại một điểm nằm bên trái trục tung.
8/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 4 (3,5 điểm)
Cho đường tròn
( ; )O R
đường kính
AB
. Vẽ tiếp tuyến
Bx
của
( )O
. Trên
cùng 1 nửa mặt phẳng bờ
AB
có chứa
Bx
, lấy điểm
M
thuộc
( )O
(
M
khác
A
và
B
) sao cho
MA MB>
. Tia
AM
cắt
Bx
tại
C
. Từ
C
kẻ tiếp
tuyến thứ hai
CD
với
( )O
(
D
là tiếp điểm)
1) Chứng minh
OC BD⊥
2) Chứng minh bốn điểm
, , ,O B C D
cùng thuộc một đường tròn
3) Chứng minh
CMD CDA=
4) Kẻ
MH
vuông góc với
AB
tại
H
. Tìm vị trí của
M
để chu vi tam
giác
OMH
đạt giá trị lớn nhất.
Lời giải
1) Chứng minh
OC BD⊥
Ta có:
,CD CB
là hai tiếp tuyến của
( )O
CD CB⇒ =
(Tính chất hai tiếp tuyến cắt nhau)
Mà
OD OB R= =
OC⇒
là đường trung trực của đoạn thẳng
DB
OC DB⇒ ⊥
x
H
M
C
D
O
B
A
9/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
2) Chứng minh bốn điểm
, , ,O B C D
cùng thuộc một đường tròn
Ta có:
OB BC⊥
(vì
BC
là tiếp tuyến của
( )O
)
OBC⇒ ∆
nội tiếp đường tròn đường kính
OC
, ,O B C⇒
cùng thuộc đường tròn đường kính
OC
(1)
Tương tự, ta có:
OD DC⊥
(vì
DC
là tiếp tuyến của
( )O
)
ODC⇒ ∆
nội tiếp đường tròn đường kính
OC
, ,O D C⇒
cùng thuộc đường tròn đường kính
OC
(2)
Từ (1) và (2) suy ra: bốn điểm
, , ,O B C D
cùng thuộc một đường tròn
đường kính
OC
x
H
M
C
D
O
B
A
10/
12
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
3) Chứng minh
CMD CDA=
Ta có:
0
90AMB =
(vì AMB∆ nội tiếp đường tròn đường kính AB )
BM AC⇒ ⊥
Xét
ABC∆
vuông tại
B
có
BM AC⊥
Theo hệ thức lượng trong tam giác vuông, ta có:
2
.CM AC CB=
Mà
( )CD CB cmt=
nên
2
.CM AC CD=
CM CD
CD AC
⇒ =
Xét
CMD∆
và
CDA∆
có:
( )
CM CD
cmt
CD AC
=
ACD
là góc chung
Do đó:
( . . )CMD CDA c g c∆ ∆
∽
CMD CDA⇒ =
x
H
M
C
D
O
B
A
11/
12
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
4) Tìm vị trí của
M
để chu vi tam giác
OMH
đạt giá trị lớn nhất.
Chu vi
OMH R OH MH∆ = + +
Ta có:
2 2 2
( ) 2 .OH MH OH OH MH MH+ = + +
(Hằng đẳng thức)
2 2 2
( ) ( ) 2 .OH MH OH MH OH MH+ = + +
2 2
( ) 2 .OH MH R OH MH+ = +
(Định lý Pitago cho
OHM∆
vuông tại
H
)
Ta lại có:
2 2 2
2 .R OH HM OH OM= + ≥
(Bất đẳng thức Cauchy)
Do đó:
2 2 2
( ) 2 . 2OH MH R OH MH R+ = + ≤
2OH MH R⇒ + ≤
⇒
Chu vi
( )
2 1 2OMH R OH MH R R R∆ = + + ≤ + = +
Suy ra: chu vi OMH∆ đạt giá trị lớn nhất là
( )
1 2 R+ khi OH MH=
OMH⇒ ∆ vuông cân tại H
0
45HOM⇒ =
Vậy chu vi OMH∆ đạt giá trị lớn nhất là
( )
1 2 R+ khi điểm M thuộc
đường tròn ( )O thỏa mãn
0
45HOM =
x
H
M
C
D
O
B
A
12/
12
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 5 (0,5 điểm)
Cho , ,x y z là các số dương thay đổi thỏa mãn: 5xy yz zx
+ + =
. Tìm giá
trị nhỏ nhất của biểu thức
2 2 2
3 3T x y z= + +
Lời giải
Áp dụng bất đẳng thức Cauchy cho 2 số dương:
2
x và
2
y , ta được:
2 2 2 2
2 2x y x y xy+ ≥ = (vì ,x y là các số dương) (1)
Áp dụng bất đẳng thức Cauchy cho 2 số dương
2
2x và
2
2
z
, ta được:
2 2
2 2
2 2 2 2
2 2
z z
x x xz+ ≥ ⋅ =
(vì
,x z
là các số dương) (2)
Áp dụng bất đẳng thức Cauchy cho 2 số dương
2
2y
và
2
2
z
, ta được:
2 2
2 2
2 2 2 2
2 2
z z
y y yz+ ≥ ⋅ =
(vì
,y z
là các số dương) (3)
Từ (1), (2) và (3) suy ra:
2 2 2
3 3 2 2 2T x y z xy xz yz= + + ≥ + +
2( )T xy xz yz⇒ ≥ + +
10T⇒ ≥
Dấu " "
=
xảy ra khi
2 2
x y=
và
2
2
2
2
z
x =
x y⇒ =
và 2z x
=
(vì
, ,x y z
là các số dương). Thay
x y=
và 2z x
=
vào
5xy yz zx
+ + =
, ta được:
2 2
5 5 1 1x x x= ⇔ = ⇔ =
(vì 0x
>
)
1; 2 2y x z x⇒ = = = =
Vậy giá trị nhỏ nhất của
T
là 10 khi
1; 2x y z= = =
| 1/12
| | Tải xuống

Có thể bạn quan tâm:

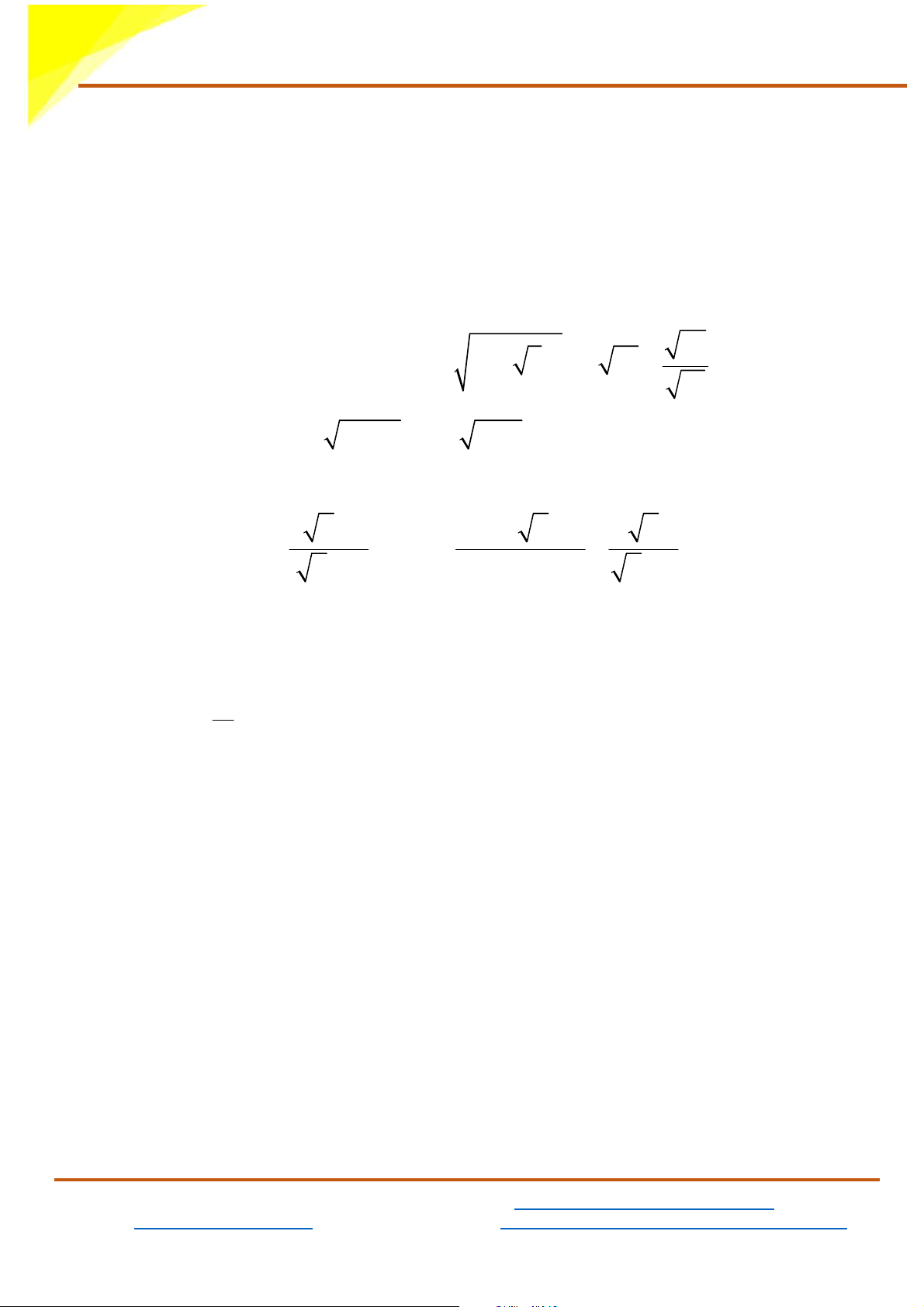
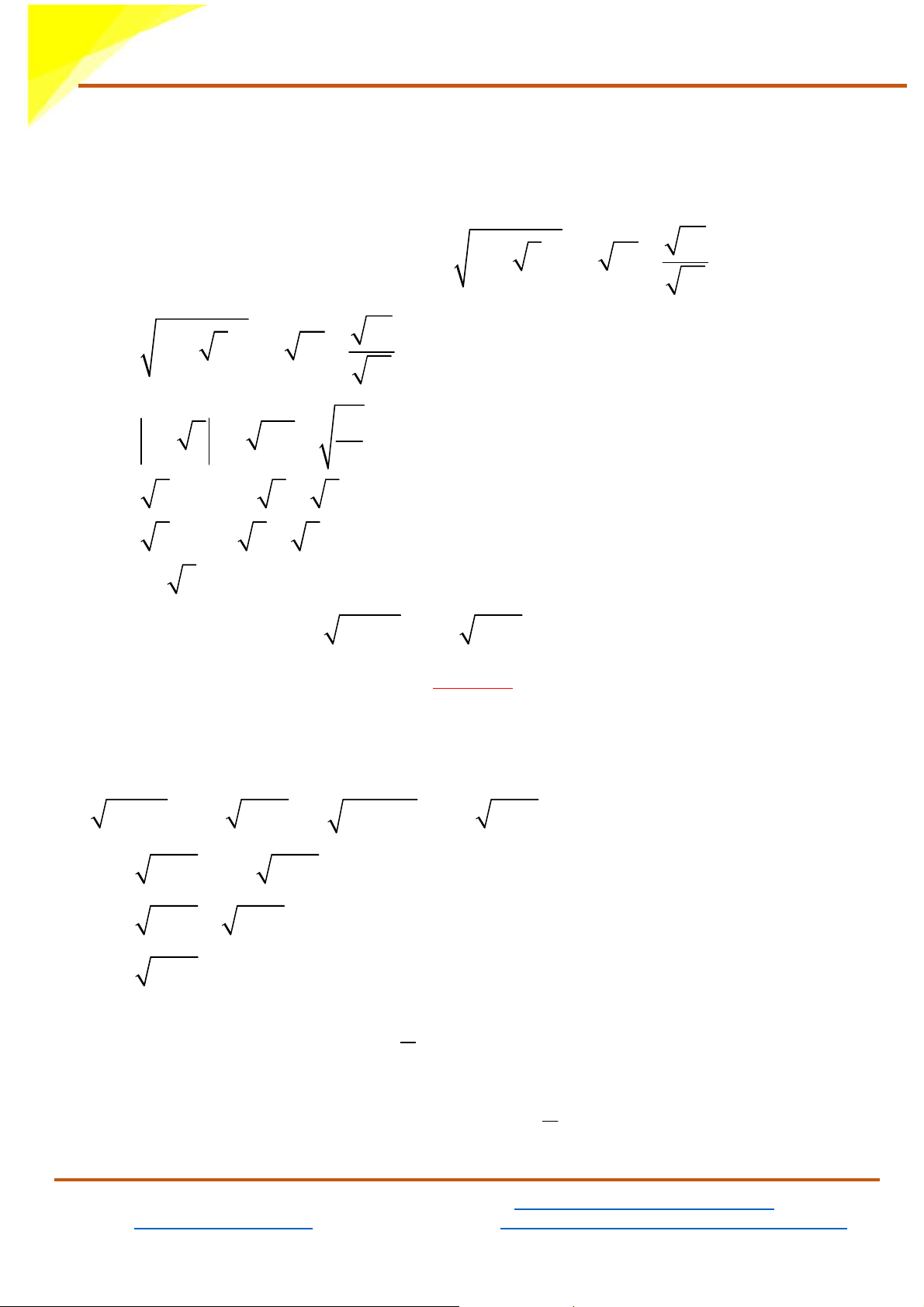
Preview text:

1/1 2
Thầy Phúc Toán – GV dạy Toán Online
ĐỀ KIỂM TRA HỌC KÌ I
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC 2018 − 2019 QUẬN ĐỐNG ĐA MÔN: TOÁN 9
Thời gian làm bài: 90 phút. Bài 1. (2,0 điểm).
1) Tính giá trị của biểu thức: M = ( − )2 33 1 3 − 3 12 + + 1 11
2) Giải phương trình: 9x − 9 −1 = x −1 Bài 2 (2,0 điểm) − + + Cho biểu thức 2 x 1 x x x A = và 2 3 9 B = −
với x ≥ 0; x ≠ 9 x − 3 x − 9 x + 3
1) Tính giá trị của A khi x = 25
2) Rút gọn biểu thức B 3) Cho A P =
. Tìm giá trị nhỏ nhất của P B Bài 3 (2,0 điểm)
Cho hàm số bậc nhất y = (m −1)x − 4 (d) (m ≠ 1)
1) Vẽ đồ thị hàm số khi m = 2
2) Tìm m để (d) song song với đồ thị hàm số y = 3 − x + 2 (d ) 1
3) Tìm m để (d) cắt đồ thị hàm số y = x − 7 (d ) tại một điểm nằm ở bên 2 trái trục tung.
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 2/1 2
Thầy Phúc Toán – GV dạy Toán Online Bài 4 (3,5 điểm)
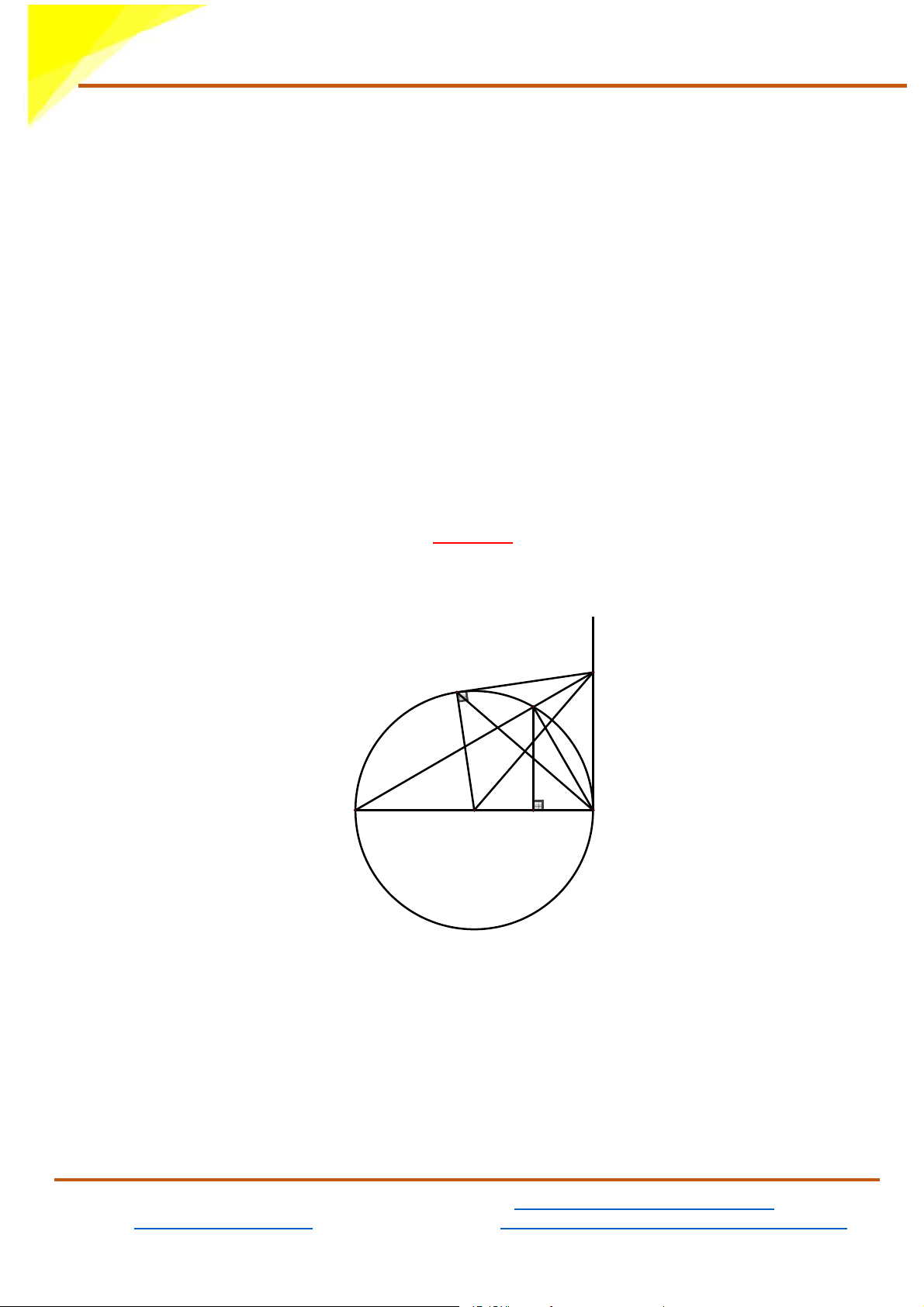
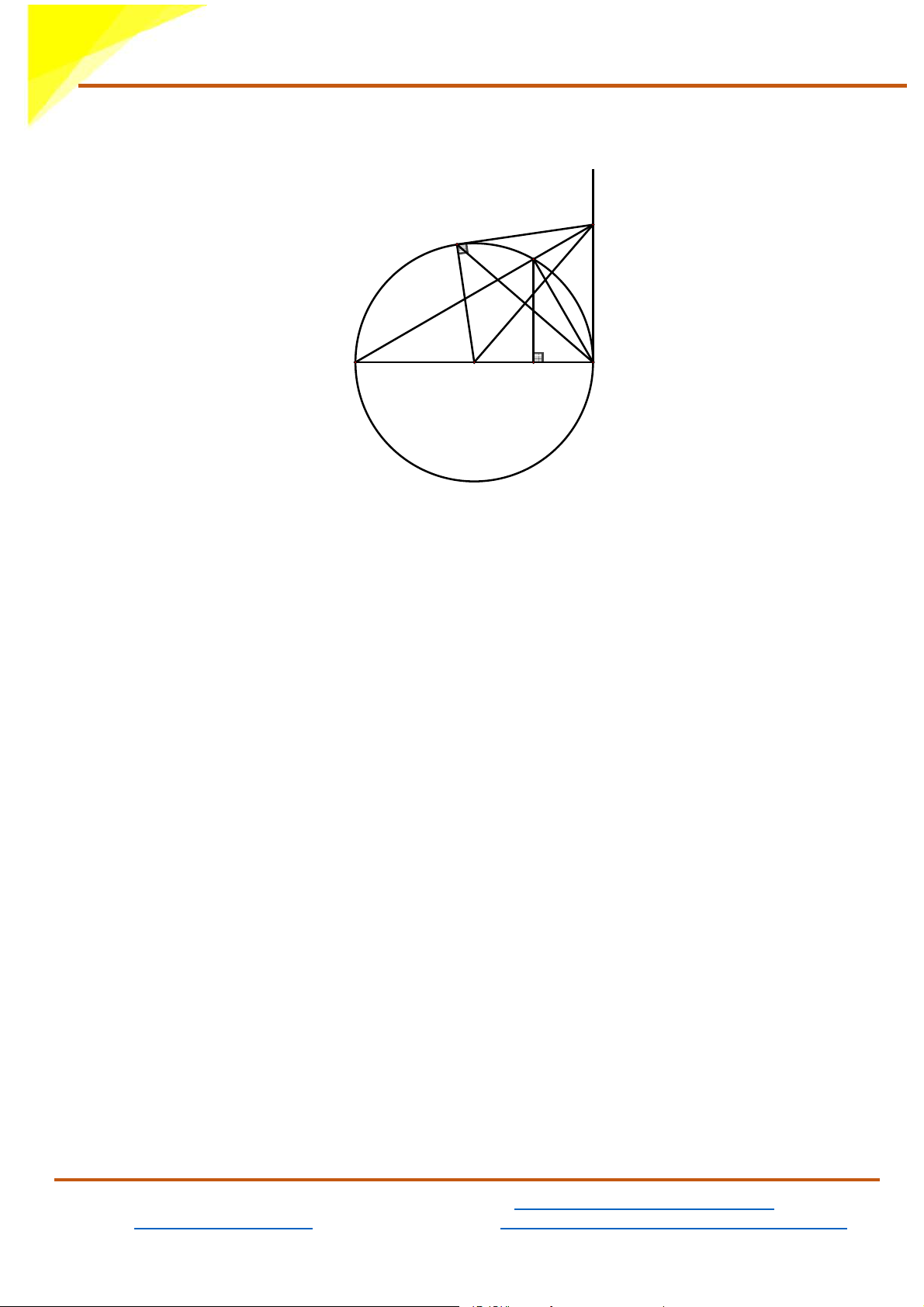
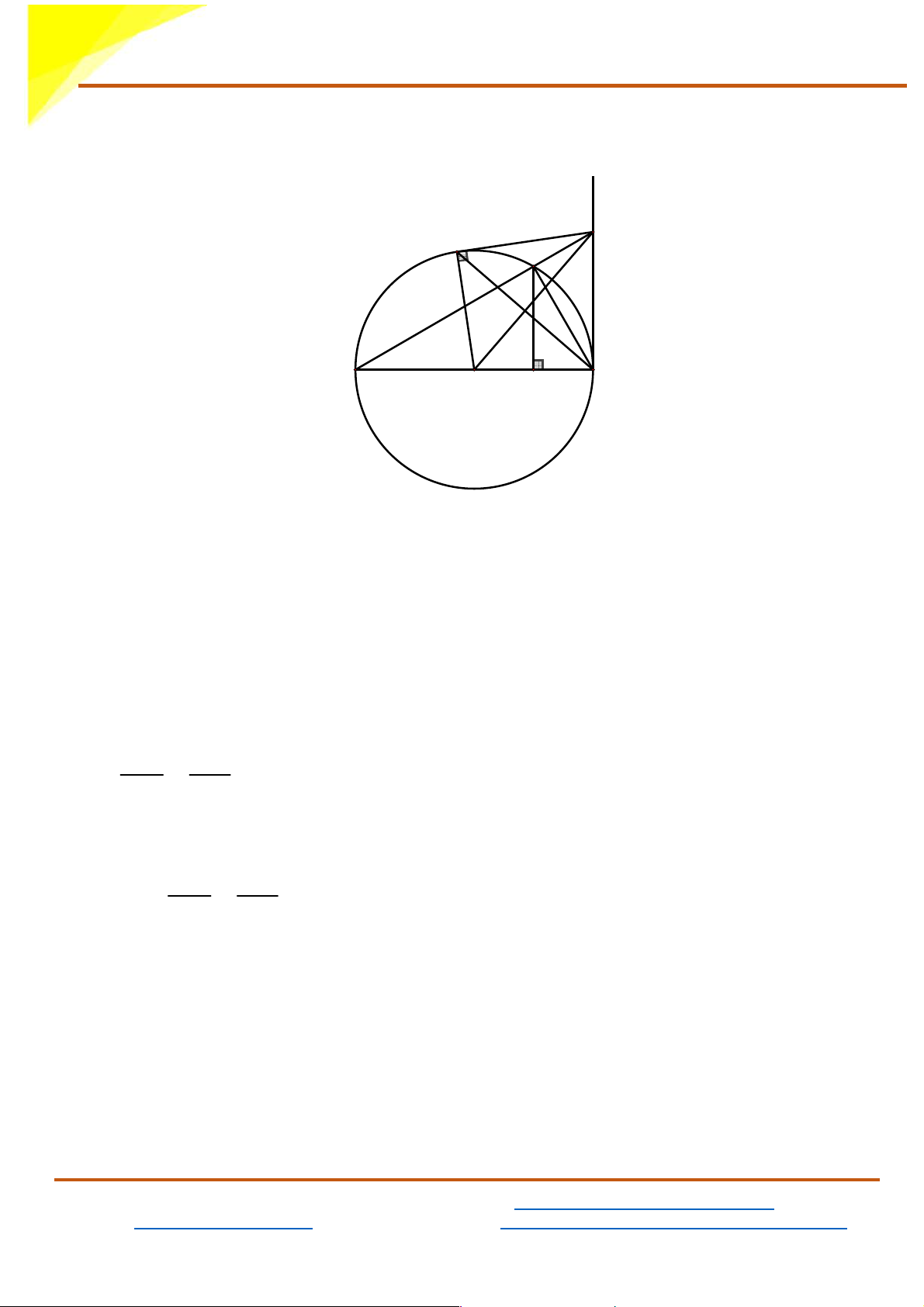
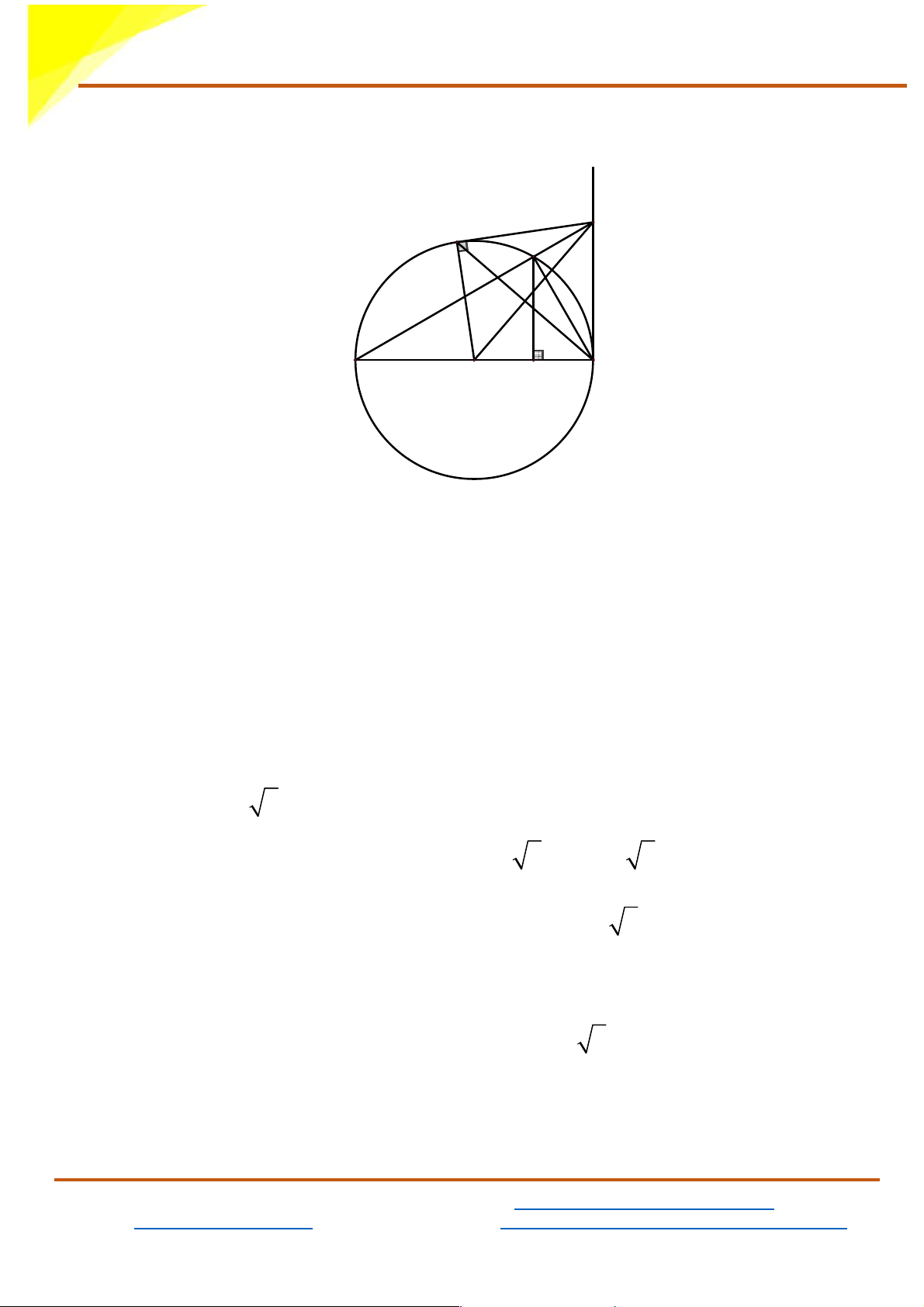
Cho đường tròn (O;R) đường kính AB . Vẽ tiếp tuyến Bx của (O). Trên
cùng 1 nửa mặt phẳng bờ AB có chứa Bx , lấy điểm M thuộc (O) (M
khác A và B ) sao cho MA > MB . Tia AM cắt Bx tại C . Từ C kẻ tiếp
tuyến thứ hai CD với (O) (D là tiếp điểm)
1) Chứng minh OC ⊥ BD
2) Chứng minh bốn điểm O,B,C,D cùng thuộc một đường tròn
3) Chứng minh CMD =CDA
4) Kẻ MH vuông góc với AB tại H . Tìm vị trí của M để chu vi tam
giác OMH đạt giá trị lớn nhất. Bài 5 (0,5 điểm)
Cho x,y,z là các số dương thay đổi thỏa mãn: xy + yz + zx = 5. Tìm giá
trị nhỏ nhất của biểu thức 2 2 2
T = 3x + 3y + z
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 3/1 2
Thầy Phúc Toán – GV dạy Toán Online HƯỚNG DẪN GIẢI Bài 1. (2,0 điểm).
1) Tính giá trị của biểu thức: M = ( − )2 33 1 3 − 3 12 + + 1 11 M = ( − )2 33 1 3 − 3 12 + + 1 11 33 M = 1 − 3 − 3 4.3 + + 1 11
M = 3 − 1 − 3.2 3 + 3 + 1
M = 3 − 1 − 6 3 + 3 + 1 M = 4 − 3
2) Giải phương trình: 9x − 9 −1 = x −1 Lời giải 9x − 9 ≥ 0 9  x ≥ 9 Điều kiện:  ⇔  ⇔ x ≥ 1 x − 1 ≥ 0 x ≥ 1  
9x − 9 − 1 = x − 1 ⇔ 9(x − 1) − 1 = x − 1
⇔ 3 x −1 −1 = x −1
⇔ 3 x −1 − x −1 = 1
⇔ 2 x −1 = 1 ⇔ 4(x −1) = 1 5
⇔ 4x − 4 = 1 ⇔ 4x = 5 ⇔ x = (thỏa điều kiện x ≥ 1) 4
Vậy phương trình có nghiệm duy nhất 5 x = 4
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 4/1 2
Thầy Phúc Toán – GV dạy Toán Online Bài 2 (2,0 điểm) − + + Cho biểu thức 2 x 1 x x x A = và 2 3 9 B = −
với x ≥ 0; x ≠ 9 x − 3 x − 9 x + 3
1) Tính giá trị của A khi x = 25
2) Rút gọn biểu thức B 3) Cho A P =
. Tìm giá trị nhỏ nhất của P B Lời giải
1) Với x = 25 (thỏa mãn điều kiện), thay vào A, ta có: 2 25 − 1 A = 25 − 3 2.5 − 1 10 − 1 9 A = = = 5 − 3 2 2
2) Rút gọn biểu thức B 2x + 3 x + 9 x B = − x − 9 x + 3 x . − x + x + ( x 3 2 3 9 ) B = ( −
x + 3)( x − 3) ( x + 3)( x − 3)
2x + 3 x + 9 − x + 3 x x + 6 x + 9 B = ( = x + 3)( x − 3) ( x +3)( x −3) ( x + )23 x + 3 B = ( = x + 3)( x − 3) x − 3
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 5/1 2
Thầy Phúc Toán – GV dạy Toán Online
3) Tìm giá trị nhỏ nhất của P A 2 x − 1 x + 3 P = = : B x − 3 x − 3 2 x − 1 x − 3 P = ⋅ x − 3 x + 3
(2 x −1)( x −3) 2 x −1 P = ( = x − 3)( x + 3) x + 3
2( x + 3) −7 2( x + 3) 7 − 7 − P = = + = 2 + x + 3 x + 3 x + 3 x + 3 − − Ta có: 7 7
x ≥ 0 ⇔ x + 3 ≥ 3 ⇒ ≥ x + 3 3 7 − −7 ⇒ P = 2 + ≥ 2 + x + 3 3 −1 ⇒ P ≥ 3 Vậy 1
MinP = − khi x = 0 3
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 6/1 2
Thầy Phúc Toán – GV dạy Toán Online Bài 3 (2,0 điểm)
Cho hàm số bậc nhất y = (m −1)x − 4 (d) (m ≠ 1)
1) Vẽ đồ thị hàm số khi m = 2
2) Tìm m để (d) song song với đồ thị hàm số y = 3 − x + 2 (d ) 1
3) Tìm m để (d) cắt đồ thị hàm số y = x − 7 (d ) tại một điểm nằm ở bên 2 trái trục tung. Lời giải
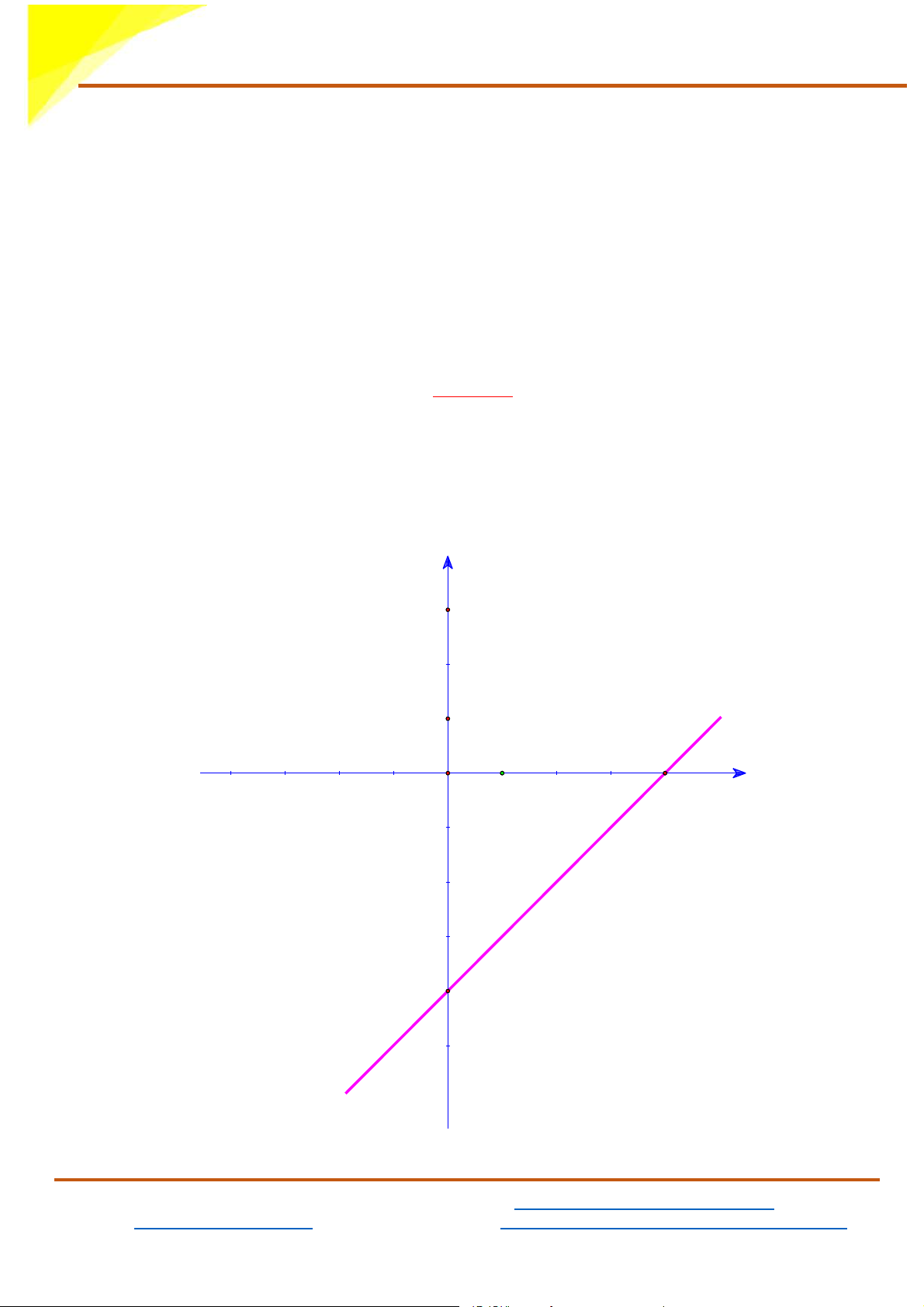
1) Thay m = 2, ta được: y = x − 4 (d)
Đồ thị hàm số y = x − 4 (d) là đường thẳng đi qua điểm (0; 4 − ) và điểm (4;0) y 3 2 1 y = x-4 O -2 -1 2 4 1 3 x -1 -2 -3 -4 -5
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 7/1 2
Thầy Phúc Toán – GV dạy Toán Online m  −1 = 3 −
2) (d)//(d ) ⇔  ⇔ m = 2 − 1 4 − ≠ 2 
Vậy (d)//(d ) khi m = 2 − 1
3) Phương trình hoành độ giao điểm của (d) và (d ): 2
(m −1)x − 4 = x − 7
⇔ mx − x − 4 = x − 7
⇔ mx − x − x = −7 + 4
⇔ x(m − 2) = 3 − 3 − ⇔ x = (m ≠ 2) m − 2
Vì giao điểm của (d) và (d ) nằm bên trái trục tung nên ta có: 2 −3 x = < 0 m − 2 ⇔ m − 2 > 0 ⇔ m > 2
Vậy m > 2 thì (d) cắt (d ) tại một điểm nằm bên trái trục tung. 2
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 8/1 2
Thầy Phúc Toán – GV dạy Toán Online Bài 4 (3,5 điểm)
Cho đường tròn (O;R) đường kính AB . Vẽ tiếp tuyến Bx của (O). Trên
cùng 1 nửa mặt phẳng bờ AB có chứa Bx , lấy điểm M thuộc (O) (M
khác A và B ) sao cho MA > MB . Tia AM cắt Bx tại C . Từ C kẻ tiếp
tuyến thứ hai CD với (O) (D là tiếp điểm)
1) Chứng minh OC ⊥ BD
2) Chứng minh bốn điểm O,B,C,D cùng thuộc một đường tròn
3) Chứng minh CMD =CDA
4) Kẻ MH vuông góc với AB tại H . Tìm vị trí của M để chu vi tam
giác OMH đạt giá trị lớn nhất. Lời giải
1) Chứng minh OC ⊥ BD x C D M A B O H
Ta có: CD,CB là hai tiếp tuyến của (O)
⇒CD =CB (Tính chất hai tiếp tuyến cắt nhau)
Mà OD =OB = R
⇒OC là đường trung trực của đoạn thẳng DB ⇒OC ⊥ DB
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 9/1 2
Thầy Phúc Toán – GV dạy Toán Online
2) Chứng minh bốn điểm O,B,C,D cùng thuộc một đường tròn x C D M A B O H
Ta có: OB ⊥ BC (vì BC là tiếp tuyến của (O) ) ⇒ O
∆ BC nội tiếp đường tròn đường kính OC
⇒O,B,C cùng thuộc đường tròn đường kính OC (1)
Tương tự, ta có: OD ⊥ DC (vì DC là tiếp tuyến của (O) ) ⇒ O
∆ DC nội tiếp đường tròn đường kính OC
⇒O,D,C cùng thuộc đường tròn đường kính OC (2)
Từ (1) và (2) suy ra: bốn điểm O,B,C,D cùng thuộc một đường tròn đường kính OC
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 10/ 12
Thầy Phúc Toán – GV dạy Toán Online
3) Chứng minh CMD =CDA x C D M A B O H Ta có: 0
AMB = 90 (vì ∆AMB nội tiếp đường tròn đường kính AB ) ⇒ BM ⊥ AC
Xét ∆ABC vuông tại B có BM ⊥ AC
Theo hệ thức lượng trong tam giác vuông, ta có: 2
CM .AC = CB
Mà CD =CB(cmt) nên 2
CM .AC = CD CM CD ⇒ = CD AC
Xét ∆CMD và ∆CDA có: CM CD = (cmt) CD AC ACD là góc chung
Do đó: ∆CMD ∽ C ∆ D ( A c.g.c) ⇒CMD =CDA
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 11/ 12
Thầy Phúc Toán – GV dạy Toán Online
4) Tìm vị trí của M để chu vi tam giác OMH đạt giá trị lớn nhất. x C D M A B O H
Chu vi ∆OMH = R +OH + MH Ta có: 2 2 2
(OH + MH ) =OH + 2OH .MH + MH (Hằng đẳng thức) 2 2 2
(OH + MH ) = (OH + MH ) + 2OH .MH 2 2
(OH + MH ) = R + 2OH .MH (Định lý Pitago cho ∆OHM vuông tại H ) Ta lại có: 2 2 2
R = OH + HM ≥ 2OH .OM (Bất đẳng thức Cauchy) Do đó: 2 2 2
(OH + MH ) = R + 2OH .MH ≤ 2R
⇒OH + MH ≤ 2R
⇒ Chu vi ∆OMH = R +OH + MH ≤ R + 2R = (1+ 2)R
Suy ra: chu vi ∆OMH đạt giá trị lớn nhất là (1+ 2)R khi OH = MH ⇒ O
∆ MH vuông cân tại H 0 ⇒ HOM = 45
Vậy chu vi ∆OMH đạt giá trị lớn nhất là (1+ 2)R khi điểm M thuộc
đường tròn (O) thỏa mãn 0 HOM = 45
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 12/ 12
Thầy Phúc Toán – GV dạy Toán Online Bài 5 (0,5 điểm)
Cho x,y,z là các số dương thay đổi thỏa mãn: xy + yz + zx = 5. Tìm giá
trị nhỏ nhất của biểu thức 2 2 2
T = 3x + 3y + z Lời giải
Áp dụng bất đẳng thức Cauchy cho 2 số dương: 2 x và 2 y , ta được: 2 2 2 2
x + y ≥ 2 x y = 2xy (vì x,y là các số dương) (1) 2
Áp dụng bất đẳng thức Cauchy cho 2 số dương z 2 2x và , ta được: 2 2 2 z z 2 2 2x + ≥ 2 2x ⋅
= 2xz (vì x,z là các số dương) (2) 2 2 2
Áp dụng bất đẳng thức Cauchy cho 2 số dương z 2 2y và , ta được: 2 2 2 z z 2 2 2y + ≥ 2 2y ⋅
= 2yz (vì y,z là các số dương) (3) 2 2 Từ (1), (2) và (3) suy ra: 2 2 2
T = 3x + 3y + z ≥ 2xy + 2xz + 2yz
⇒T ≥ 2(xy + xz + yz) ⇒T ≥ 10 2 Dấu z " = " xảy ra khi 2 2 x = y và 2 2x = 2
⇒ x = y và z = 2x (vì x,y,z là các số dương). Thay x = y và z = 2x vào
xy + yz + zx = 5 , ta được: 2 2
5x = 5 ⇔ x = 1 ⇔ x = 1 (vì x > 0 )
⇒ y = x = 1; z = 2x = 2
Vậy giá trị nhỏ nhất của T là 10 khi x = y = 1; z = 2
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017