THPT NGUYỄN BỈNH KHIÊM
ĐỀ THI HỌC KỲ II TỔ TOÁN
NĂM HỌC 2019 – 2020
Môn: Toán - Lớp 11 - Chương trình chuẩn ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút (không kể thời gian phát đề) Mã đề thi
Họ và tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Lớp: . . . . . . . . . . . . 297
PHẦN 1. TRẮC NGHIỆM (5,0 ĐIỂM)
Câu 1. Đạo hàm của hàm số 2
y = 1− 2x là 2 − x 2x 4 − x 1 A. y ' = . B. y ' = . C. y ' = . D. y ' = . 2 1− 2x 2 1− 2x 2 1− 2x 2 2 1− 2x
Câu 2. Cho đồ thị hàm số 3 2
y = x + 3x − 20(C) , có bao nhiêu tiếp tuyến của đồ thị (C) song song đường
thẳng d : y = 24x − 48 ? A. 2. B. 3. C. 0. D. 1.
f (x) − f (4)
Câu 3. Cho hàm số y = f (x) xác định trên  và thỏa mãn lim
= 3. Khẳng định nào sau đây x→4 x − 4 đúng? A. '
f (x) = 3. B. ' f (3) = 4. C. ' f (4) = 3.
D. f (3) = 4 .
Câu 4. Giới hạn lim(3− 4x) bằng x→2 A. 11. B. 5. C. 3. D. 5 − .
Câu 5. Cho f x 3sin x cos x . Rút gọn biểu thức A  f  x f x A. 2
B. 4cos x .
C. 6sin x  4cos x . D. 0 . Câu 6. Giới hạn ( 2
lim 3n − 2n + 4) bằng A. −∞ . B. 3. C. 0 . D. +∞
Câu 7. Cho hình chóp S.ABCD đáy là hình chữ nhật, cạnh bên SA vuông góc với mặt phẳng
đáy, SA = AB = a 2 , AD = a . Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng A. 0 45 . B. 0 90 . C. 0 30 . D. 0 60 . a 2
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh với AC = , cạnh bên SA vuông góc 2
đáy, SB tạo đáy một góc 0
60 . Khoảng cách giữa AD và SC bằng a 2 a 3 a a 3 A. . B. . C. . D. . 2 2 3 4
Câu 9. Hàm số nào sau đây liên tục tại x = 5? 4 2 A. x − 2x +1 − − y 2 = B. 1 y = tan . C. 3x 4 y = . D. x y = . x − 5 x − 5 x + 5 2 x − 25 2
Câu 10. Cho hai số thực
x ax b 2
a và b thỏa lim  6. Giá trị của 2
a  b bằng x 4 x  4 A. 8. B. 38. C. 10. D. 4.
Câu 11. Cho hai đường thẳng a,b và mp(P). Chỉ ra mệnh đề đúng trong các mệnh đề sau:
A. Nếu a// (P) và b ⊥ a thì b// (P) .
B. Nếu a// (P) và b ⊥ a thì b ⊥ (P) .
C. Nếu a// (P) và b ⊥ (P) thì a ⊥ b .
D. Nếu a ⊥ (P) và b ⊥ a thì b// (P) . f x15
3 5 f x11  4
Câu 12. Cho đa thức f x thỏa mãn lim  12. Tính L  lim . x 3 x 3 2 x 3 x  x 6 A. 3 L  . B. 1 L  . C. 1 L  . D. 5 L  . 40 20 4 4 Trang 1/2 - Mã đề 297 2 Câu 13. Giới hạn 3x − 2x −1 lim bằng 2 x 1 → x −1 A. 2 . B. 2 . C. 3. D. 2 − . 3 +
Câu 14. Có bao nhiêu giá trị nguyên của tham số m để hàm số x 2 y =
có đạo hàm âm trên khoảng x − m (4;+∞) A. vô số. B. 6 . C. 7 . D. 5.
 x + khi x ≥
Câu 15. Cho f (x) 2 3 1 =
. Trong các khẳng định sau khẳng định nào đúng? 5   − 4x khi x <1
A. f (x) liên tục trên . 
B. f (x) liên tục trên [1;+∞).
C. f (x) liên tục tại x =1.
D. f (x) liên tục trên(−∞ ] ;1 .
Câu 16. Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình vuông.Khẳng định nào sau đây sai
A. AC ⊥ (SBD).
B. BC ⊥ (SAB).
C. CD ⊥ (SAD).
D. BD ⊥ (SAC).
Câu 17. Cho hình chóp S.ABCD đáy là hình chữ nhật, cạnh bên SA vuông góc với mặt phẳng
đáy, SA = AB = a 2 , AD = a . Khoảng cách từ trung điểm của SC đến mặt phẳng (SBD) bằng
A. a 3 . B. a 2 . C. a 2 . D. a 6 . 4 2 4 6
Câu 18. Một vật chuyển động theo quy luật s(t) 1 3 2 1
= − t + 2t − với t (giây) là khoảng thời gian tính từ khi 3 3
vật bắt đầu chuyển động và s (m) là quãng đường vật đi được trong khoảng thời gian t . Hỏi trong khoảng 10
(giây) kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng A. 4. B. 5. C. 9. D. 14.
Câu 19. Cho tứ diện đều ABCD. Cóc giữa 2 đường thẳng AB và CD bằng A. 0 90 B. 0 45 C. 0 60 D. 0 30
Câu 20. Đạo hàm của hàm số + y = (x + )
1 2 − x có dạng ax b . Tổng 2a + 4b bằng 2 − x A. 3. B. 9. C. 3. − D. 9. −
PHẦN 2. TỰ LUẬN (5,0 ĐIỂM)
Bài 1: (1,5 điểm) Tìm các giới hạn sau : 2 a/ 3x − 4x +1 lim b/ 2x − 7 lim x 1 → x −1 x→3 x − 3
Bài 2: (2,0 điểm) Tìm đạo hàm của các hàm số sau : a/ y = x2 3 − 4 x − 2
b/ y = 4sin x − 5cos3x + 2
Bài 3: (1,5 điểm) Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, cạnh SA vuông góc với đáy, 1 góc giữa SC và đáy là 0
60 , M là trung điểm SD và I thuộc cạnh BM sao cho BI = BM 4
a/ Chứng minh BC ⊥ (SAB) .
b/ Tính khoảng cách từ I đến mặt phẳng (SDC)
------------- HẾT ------------- Trang 2/2 - Mã đề 297
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ 2 TOÁN 11 - NĂM HỌC 2019-2020 ĐỀ 297
PHẦN 1: TRẮC NGHIỆM (6,0 điểm)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
A D C D D D D D C C C C B B B A C A A A
PHẦN 2: TỰ LUẬN (5,0 điểm) Câu 1 ĐỀ: 297 Điểm
1. Tìm các giới hạn sau : T1,5 2 3x − 4x +1 (x − ) 1 (3x − ) 1 a/ lim = lim = lim(3x − )
1 (0,5) = 2 (0,25)........................... x 1 → x 1 → x 1 x −1 x −1 → 0,75 b/ 2x − 7 lim
. Ta có lim(2x − 7) = 1
− < 0............................................................................ x→3 x − 3 x→3 0,25
lim x − 3 = 0 và x − 3 > 0, x
∀ ≠ 3 ...................................................... 0,25 x→3 Vậy 2x − 7 lim
= −∞ ............................................................................................................... 0,25 x→3 x − 3
Câu 2 Tìm đạo hàm của các hàm số sau : T2,0 2 2
1a/ y = 3x − 4 x − 2 . Ta có: y' = 6x −
(Sai mỗi chỗ trừ 0,5)........ 1,0 x ( x − x + )' 4sin 5cos3 2
1b/ y = 4sin x − 5cos3x + 2 . Ta có: y' = (0,5) 1.0
2 4sin x − 5cos3x + 2 4cos x + = 15sin3x (0,5).......
2 4sin x − 5cos3x + 2
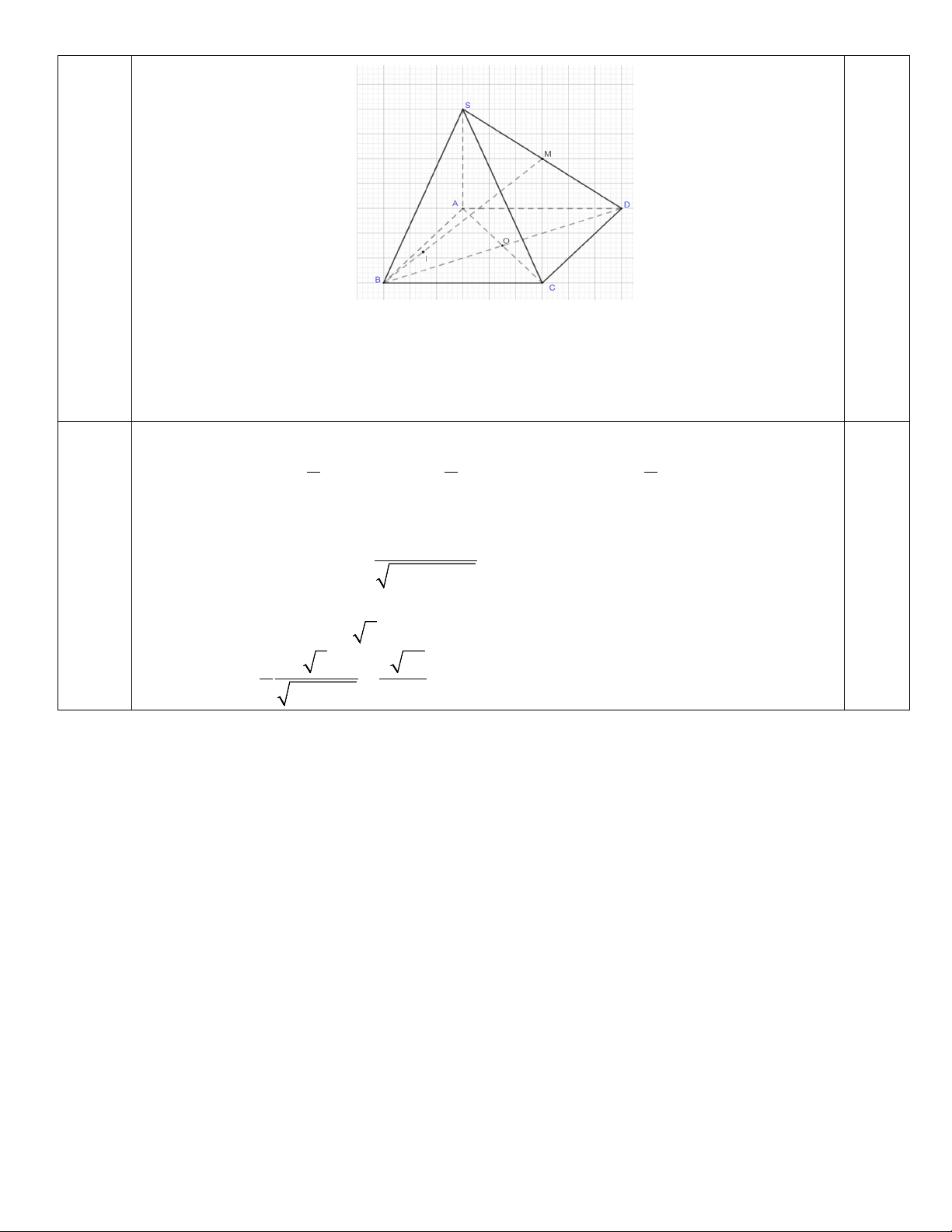
Câu 3 Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, cạnh SA vuông T1,5
góc với đáy, góc giữa SC và đáy là 0
60 , M là trung điểm SD và I thuộc cạnh BM sao cho 1 BI = BM 4
a/ Chứng minh BC ⊥ (SAB).
b/ Tính khoảng cách từ I đến mặt phẳng (SDC) 0,25 0,5
a/ Chứng minh BC ⊥ (SAB) .
CB ⊥ BA (V× ABCD lµ h×nh vu«ng) 
+ Ta có CB ⊥ SA (V× SA ⊥ (ABCD))
⇒ CB ⊥ (SAB) …………………………. BA∩ SA =  A b/ 3 3
Ta có d (I;(SCD)) = d (B;(SCD)) = d ( ;
A (SCD)) (Vì MI = 3 MB, AB / / CD) 4 4 4 0,25 Mà DC ⊥ (S )
AD nên (SDC) ⊥ (SA )
D ,kẻ AH ⊥ SD thì AH ⊥ (SC ) D . SA AD 0,5 Do đó d( ;
A (SCD)) = AH = 2 SA + 2 AD
Hình chiếu của SC lên (ABCD) là AC Nên góc giữa SC và (ABCD) là SCA = 0 60 Do đó SA = 0 AC tan60 = a 6 ( ( )) = 3 a 6.a d I SCD = 3 42 ; a . 2 4 6a + 2 a 28
Document Outline

• Made 297
• ĐỀ THI VÀ ĐÁP ÁN HK2 KHỐI 11 NĂM 2020