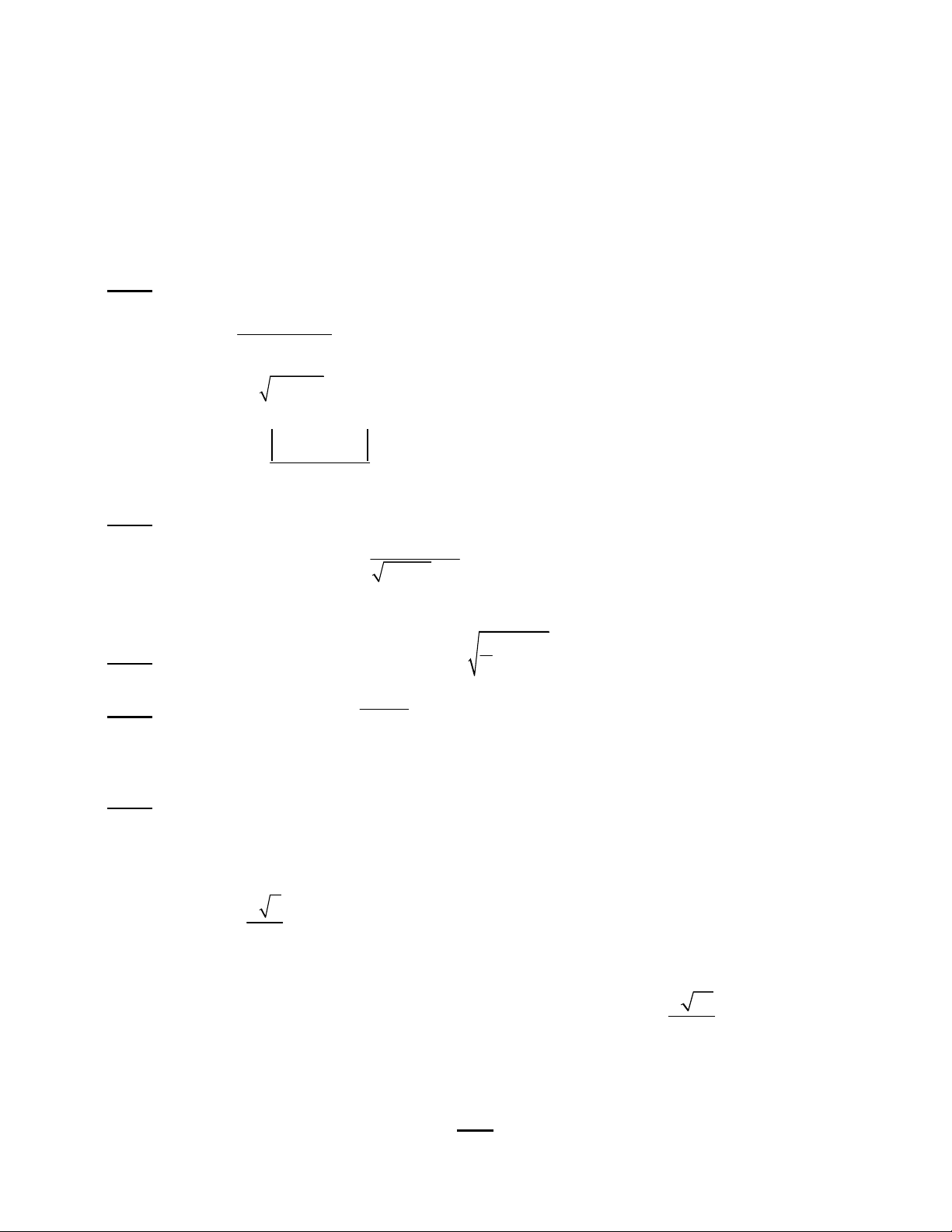


Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM
ĐỀ KIỂM TRA HỌC KÌ II
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
Năm học: 2019 – 2020
Môn TOÁN – Khối: 11 Thời gian: 90 phút
(Không kể thời gian phát đề)
Họ và tên học sinh: ……………………………………………………Số báo danh:………………………… Bài 1: Tính 2 x 9x 14 a) A lim . (1 điểm) x 2 x 2 b) 3 3 B lim
8x 1 x. (1 điểm) x 2 x 7x 12 c) C lim . (1 điểm) 3 x 3 x
Bài 2: Định a để hàm số sau đây liên tục tại xo = 4: x 4 x > 4 f x x 13 3 . (1 điểm) 2
x 2a x 4 1
Bài 3: Tìm đạo hàm của hàm số y f x tan x. (1 điểm) x 2x 5
Bài 4: Cho hàm số y f x
có đồ thị (C). Viết phương trình tiếp tuyến () x 3
của đồ thị (C) biết () song song với đường thẳng (D): y = 11x. (1 điểm)
Bài 5: Cho hình chóp S.ABC có ABC vuông cân tại C, CA = a; SC(ABC).
a) Chứng minh: AC(SBC). (1 điểm)
b) Gọi I là trung điểm của AB. Chứng minh: (SCI)(SAB). (1 điểm) a 6 c) Cho SC
. Tính SAB; ABC . (1 điểm) 2
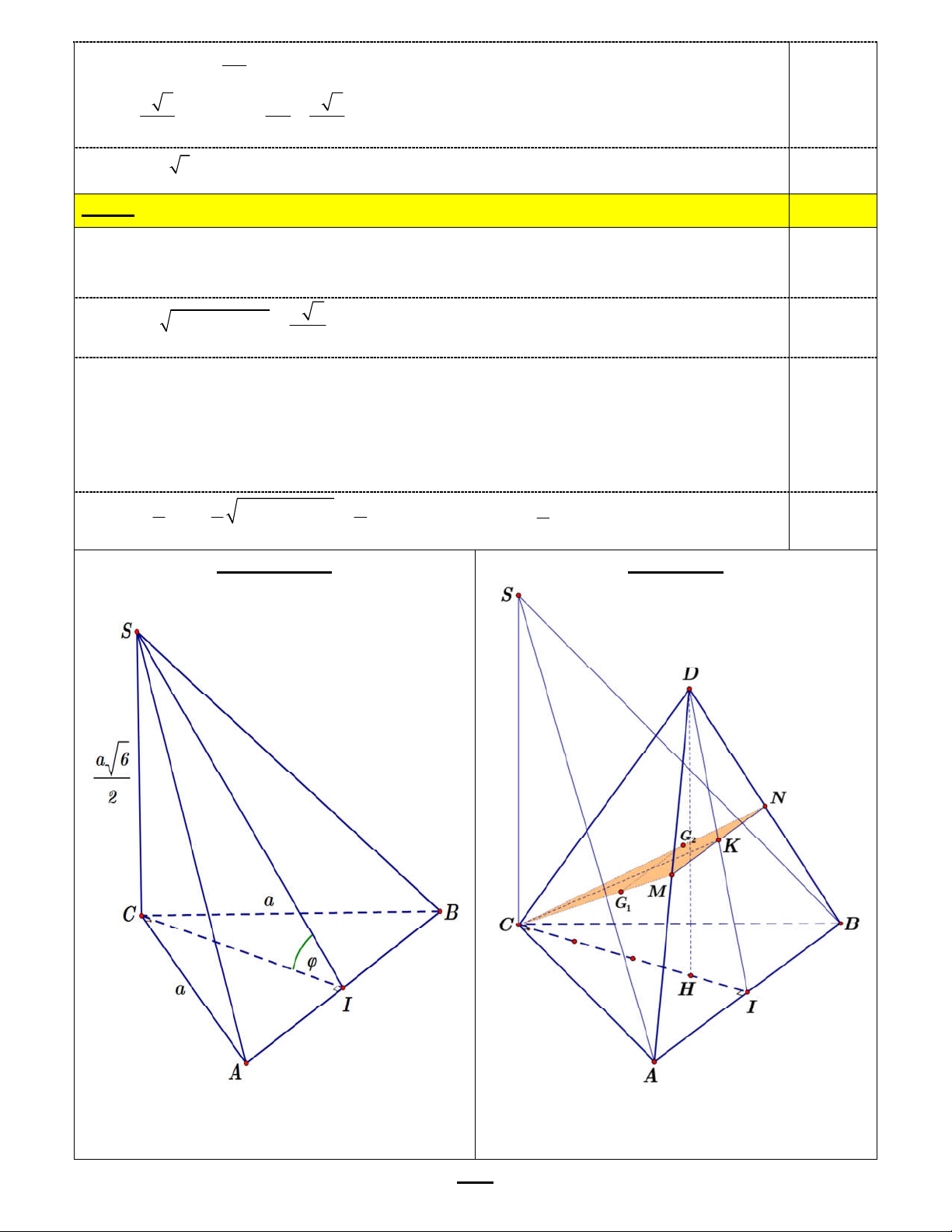
d) Gọi H là điểm thuộc đoạn CI sao cho CH = 3HI. Trên đường thẳng đi qua H và a 14
vuông góc với mặt phẳng (ABC), lấy điểm D sao cho DH = . Gọi G 8 1 và G2
lần lượt là trọng tâm của các tam giác DAC và DBC. Tính khoảng cách từ điểm
A đến mặt phẳng (CG1G2). (1 điểm) HẾT
ĐÁP ÁN & BIỂU ĐIỂM (Đề 1) Bài 1: 3đ 2 x 9x 14
Câu a: A lim 1đ x 2 x 2
x 2 x 7 lim 0.5 x 2 x 2 lim x 7 0.25 x 2 = 5. 0.25 Câu b: 3 3 B lim 8x 1 x x 1đ 1 3 lim . x 8 x 0.25 3 x x 1 lim . x 3 8 1 0.25 3 x x 1
= + ∞. (Vì lim x ; lim 3 8 1 1 0 ) 0.25+0.25 3 x x x 2 x 7x 12 Câu c: C lim 1đ x 3 x 3
x 3x 4 lim 0.25 3 x 3 x
x 3 x 4 lim 0.25 3 x 3 x lim x 4 0.25 x 3 = 1. 0.25 Bài 2: 1đ
f(4) = 16 + 2a 0.25 lim
f x lim 2
x 2a 16 2a 0.25 x 4 x 4 x 4 lim f x lim lim x 13 3 6 0.25 x 4 x 4 x 13 3 x 4
Ycbt a = 5. 0.25 1
Bài 3: y f x tan x 1đ x / 1 tan x 1 2 1 tan x / x 2 0.25x4 y x . 1 1 2 tan x 2 tan x x x 2x 5
Bài 4: y f x . 1đ x 3 / 11 f x 0.25 x 32
Gọi xo là hoành độ tiếp điểm của () và (C). Ta có: 0.25 /
f x k o (D) = 11 11 x 4 0 1 1 0.25 x 32 x 2 0 0
Vậy có 2 tiếp tuyến thỏa ycbt: (1): y = 11x + 57 ; (2): y = 11x + 13. 0.25 Bài 5: 4đ
Câu a: Chứng minh: AC (SBC). 1đ
ACCB (do ABC vuông cân tại C) (1) 0.25
ACSC (do SC(ABC)) (2) 0.25
Từ (1),(2) suy ra: AC(SBC). 0.5
Câu b: Chứng minh: (SCI) (SAB). 1đ
ABCI (do ABC vuông cân, I là trung điểm của AB) (3) 0.25
ABSC (do SC(ABC)) (4) 0.25
Từ (3)(4) suy ra: AB(SCI) 0.25
Vậy: (SCI)(SAB). 0.25
Câu c: Tính SAB; ABC . 1đ
(SAB)(ABC) = AB AB(SCI) 0.25
(SCI)(SAB) = SI, (SCI)(ABC) = CI
Vậy: SAB; ABC
SI;CI
SIC. (do SC(ABC) SCCI SIC nhọn) 0.25 SC
SCI : tanSIC IC 0.25 a 6 AB a 2 SC
gt ; IC ABC vuoâng taïi C 2 2 2
tanSIC 3 ; 60 . o SAB ABC 0.25
Câu d: Tính khoảng cách từ A đến mặt phẳng (CG1G2) 1đ
Gọi M, N lần lượt là trung điểm của DA và DB, K = DIMN. Khi đó: 0.25
G1G2//MN//AB AB//(CG1G2) mà IAB nên d(A,(CG1G2)) = d(I, (CG1G2)). a 2 2 2
DC DH HC
CI DIC cân tại C DI CK. 0.25 2
G1G2//AB mà AB(SCI) nên G1G2 (DCI) (CG1G2)(DCI)
(CG1G2)(DCI) = CK 0.25
DI(DIC): DI CK
DI (CG1G2) IK (CG1G2) tại K d(I, (CG1G2)) = IK. 1 1 a a 2 2 IK DI DH HI
d(A,(CG 0.25 2 2 4 1G2)) = . 4 Hình câu abc Hình câu d HẾT




