Đề thi HK2 Toán 11 năm 2020 – 2021 trường THPT Nguyễn Công Trứ – TP HCM
Ngày … tháng 04 năm 2021, trường THPT Nguyễn Công Trứ, quận Gò Vấp, thành phố Hồ Chí Minh tổ chức kỳ thi kiểm tra chất lượng môn Toán 11 giai đoạn cuối học kỳ 2 năm học 2020 – 2021
Chủ đề: Đề HK2 Toán 11 391 tài liệu
Môn: Toán 11 3.3 K tài liệu
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ II (NĂM HỌC 2020 – 2021) THÀNH PHỐ HỒ CHÍ MINH MÔN: TOÁN - KHỐI 11
TRƯỜNG THPT NGUYỄN CÔNG TRỨ
Thời gian làm bài: 90 phút, không kể thời gian giao đề ĐỀ CHÍNH THỨC Câu 1 (2.0 điểm): Tìm các giới hạn sau: x 6 3 a) 2 lim ( x 4x 1 5x) b) lim x 2 x 3 x 7x+12 Câu 2 (1.0 điểm):
Chứng minh rằng phương trình x6 + 2021.sin2x – 1 = 0 có nghiệm x. Câu 3 (1.5 điểm): a) Cho hàm số 2
y 4x x . Giải bất phương trình / y 0
b) Cho y 4sin x 3cos x 5x . Chứng minh rằng: /
0 y 10 với mọi giá trị của x. Câu 4 (1.5 điểm): Cho đồ thị hàm số 3
(C) : y f (x) 2x 7x 1. Viết phương trình tiếp tuyến của (C) biết
tiếp tuyến song song với đường thẳng (d): y = – x + 5. Câu 5 (4.0 điểm):
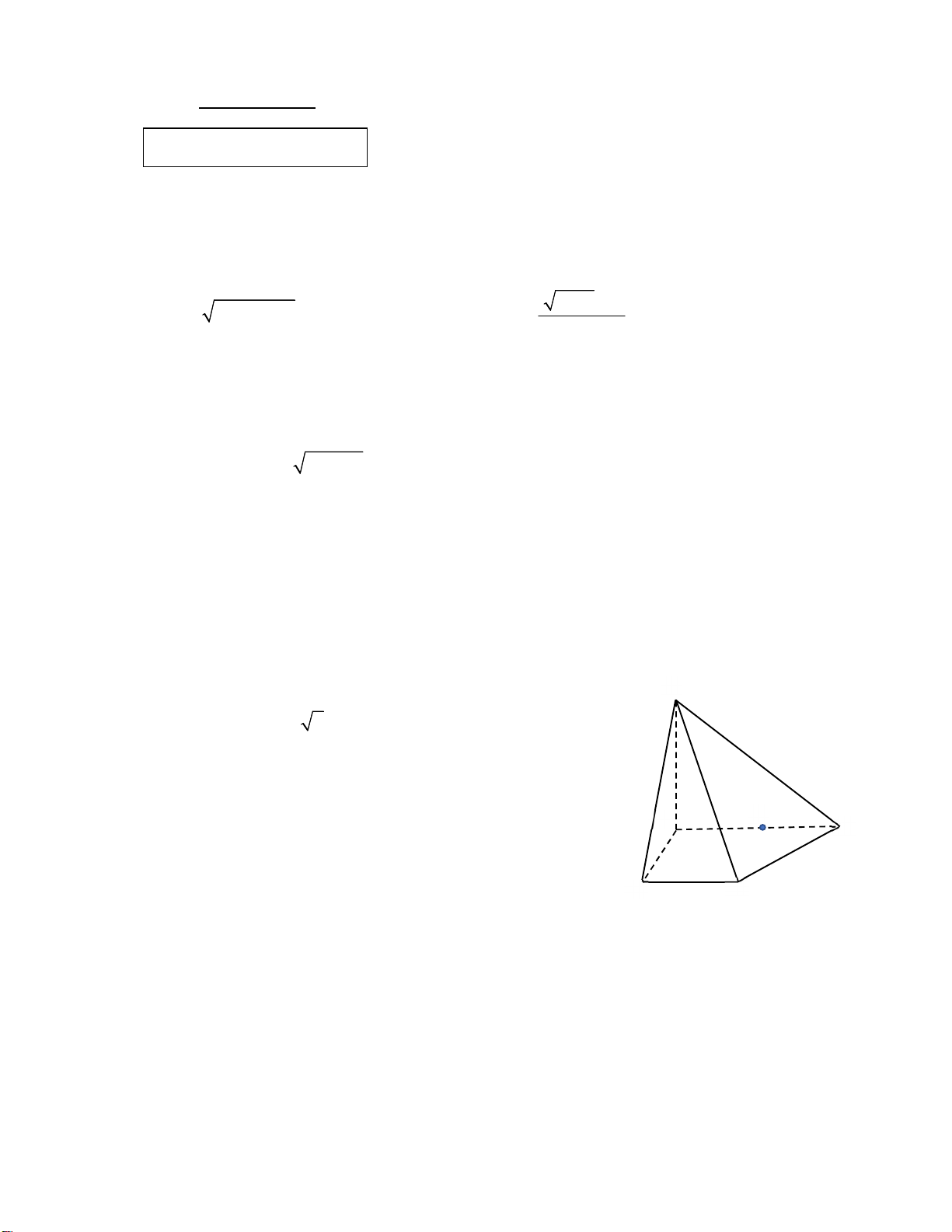
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng
(ABCD) và ABCD là hình thang vuông tại A, B. Biết AB = BC S
= a, AD 2a .SA a 2 . Gọi K là trung điểm của AD.
a) Chứng minh: BK (SAC), (SBC) (SAB)
b) Chứng minh : tam giác SCD vuông tại C.
c) Xác định và tính góc giữa (SCD) và (ABCD). A K D
d) Tính khoảng cách từ điểm K đến (SCD). B C -HẾT-
Họ và tên thí sinh:…………………………………….. SBD:………………………………