Đề thi HK2 Toán 11 năm học 2016 – 2017 trường THPT chuyên Nguyễn Huệ – Hà Nội

Đề thi HK2 Toán 11 năm học 2016 – 2017 trường THPT chuyên Nguyễn Huệ – Hà Nội gồm 50 câu hỏi trắc nghiệm, có đáp án và lời giải chi tiết.

Trích một số bài toán trong đề:
+ Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, SA = SB = SC. Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 45 độ. Tính theo a khoảng cách từ điểm S đến mặt phẳng (ABC).
+ Trong các mệnh đề sau, mệnh đề nào đúng?

Chủ đề:

Đề HK2 Toán 11 391 tài liệu

Môn:

Toán 11 3.3 K tài liệu

Thông tin:
22 trang 1 năm trước
Tác giả:
K
Kim Oanh
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Đề thi HK2 Toán 11 năm học 2016 – 2017 trường THPT chuyên Nguyễn Huệ – Hà Nội

Đề thi HK2 Toán 11 năm học 2016 – 2017 trường THPT chuyên Nguyễn Huệ – Hà Nội gồm 50 câu hỏi trắc nghiệm, có đáp án và lời giải chi tiết.

Trích một số bài toán trong đề:
+ Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, SA = SB = SC. Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 45 độ. Tính theo a khoảng cách từ điểm S đến mặt phẳng (ABC).
+ Trong các mệnh đề sau, mệnh đề nào đúng?

64 32 lượt tải Tải xuống

Chủ đề: Đề HK2 Toán 11 391 tài liệu

Môn: Toán 11 3.3 K tài liệu

Thông tin:

22 trang 1 năm trước

Tác giả:

Profile Kim Oanh
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 1/22 Mã đề 483
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI KỲ THI HỌC KỲ 2 LỚP 11 NĂM HỌC 2016-2017
THPT CHUYÊN NGUYỄN HUỆ Môn thi: TOÁN
ĐỀ CHÍNH THỨC Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ và tên thí sinh: …………………………………………………………
Số báo danh:………………………………………………………………
Câu 1: Viết phương trình tiếp tuyến của đồ thị hàm số
3 2
( ) 2 3 1
f x x x x
= − + +
tại điểm có hoành độ
0
2
x
=
A.
7
y x
= − −
. B.
y x
= −
. C.
7 7
y x
= −
. D.
9
y x
= − +
.
Câu 2: Tính giới hạn
0
1 1
lim ?
x
x
x
→
+ −
A.
→
+ −
= −
x 0
1 x 1 1
lim
x 2
. B.
→
+ −
= +∞
x 0
1 x 1
lim
x
. C.
→
+ −
=
x 0
1 x 1
lim 0
x
. D.
→
+ −
=
x 0
1 x 1 1
lim
x 2
.
Câu 3: Cho hàm số:
(
)
3
f x x
= +
. Tính
(
)
(
)
1 4 1
f f
′
+
A.
1
. B.
3
. C.
1
4
. D.
0
.
Câu 4: Cho hàm số:
3 2
( ) 3 4.
f x x x
= − +
Tính
(1).
f
′
A.
3
−
. B.
0
. C.
9
. D.
3
.
Câu 5: Cho dãy số
(
)
n
u
với
( )
1 sin
n
n
u
n
π
= − , chọn khẳng định đúng trong các khẳng định sau?
A. Dãy số
(
)
n
u
là dãy số tăng.
B. Dãy số
(
)
n
u
bị chặn dưới nhưng không bị chặn trên.
C. Dãy số
(
)
n
u
bị chặn.
D. Dãy số
(
)
n
u
bị chặn trên nhưng không bị chặn dưới.
Câu 6: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
A
,
AB a
=
,
SA SB SC
= =
.
Góc giữa đường thẳng
SA
và mặt phẳng
(
)
ABC
bằng
0
45
. Tính theo
a
khoảng cách từ điểm
S
đến mặt phẳng
(
)
ABC
.
A.
3
3
a
. B.
3
a
. C.
2
a
. D.
2
2
a
.
Câu 7: Cho hàm số
(
)
4 2
2 1
f x x x
= − +
. Tìm
x
để
(
)
0
f x
′
>
.
A.
(
)
(
)
1;0 1;x
∈ − ∪ +∞
. B.
(
)
1;1
x ∈ − . C.
(
)
(
)
; 1 0;1
x ∈ −∞ − ∪ .D.
x
∈
ℝ
.
Câu 8: Tìm tất
cả các giá trị của
x
để ba số
2
1 , ,1
x x x
− +
theo thứ tự lập thành cấp số cộng?
A.
1
x
= ±
. B.
2
x
= ±
. C.
1
x
=
. D.
1
x
= −
.
Câu 9: Trong các dãy số sau, dãy số nào không là cấp số cộng?
A.
1 1 1 1 1
; ; ; ;
2 4 6 8 10
. B.
1 3 5 7 9
; ; ; ;
2 2 2 2 2
. C.
8; 6; 4; 2;0
− − − −
. D.
2; 2; 2; 2; 2
.
Câu 10: Tính đạo
hàm của hàm số
2sin 3 cos 2
y x x
= +
A.
2cos3 sin 2
y x x
′
= −
. B
2 cos3 sin 2
y x x
′
= +
.
C.
6cos3 2sin 2
y x x
′
= −
. D.
6cos3 2sin 2
y x x
′
= − +
.
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 2/22 Mã đề 483
Câu 11: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Hình chiếu vuông góc của
S
lên
(
)
ABC
trùng với trung điểm
H
của cạnh
BC
. Biết tam giác
SBC
là tam giác đều. Tính số đo
của góc giữa
SA
và
(
)
ABC
A.
30
°
. B.
45
°
. C.
60
°
. D.
90
°
.
Câu 12: Tính giới hạn
(
)
2
lim
− −
n n n
?
A.
(
)
2
lim
− − = +∞
n n n . B.
(
)
2
lim 1
− − = −
n n n .
C.
(
)
2
1
lim
2
− − = −
n n n . D.
(
)
2
lim 0
− − =
n n n .
Câu 13: Cho hı
nh lăng tru
.
′ ′ ′
ABC A B C
co
tâ
t ca
ca
c ca
nh đê
u bă
ng
a
. Go
c ta
o bơ
i ca
nh bên va
mă
t
phă
ng đa
y bă
ng
30
°
. Hı
nh chiê
u
H
cu
a
′
A
lên mă
t phă
ng
(
)
ABC
thuô
c đươ
ng thă
ng
BC
.
Tı
nh khoa
ng ca
ch tư
B
đê
n mă
t phă
ng
(
)
′ ′
ACC A
A.
21
7
a
. B.
3
4
a
. C.
3
2
a
. D.
21
14
a
.
Câu 14: Trong ca
c mê
nh đê
sau, mê
nh đê
na
o đu
ng?
A. Hai đươ
ng thă
ng cu
ng vuông go
c vơ
i mô
t đươ
ng thă
ng thı
song song vơ
i nhau.
B. Hai đươ
ng thă
ng cu
ng vuông go
c vơ
i mô
t đươ
ng thă
ng thı
vuông go
c vơ
i nhau.
C. Mô
t đươ
ng thă
ng vuông go
c vơ
i mô
t trong hai đươ
ng thă
ng vuông go
c thı
song song vơ
i
đươ
ng thă
ng co
n la
i.
D. Mô
t
đươ
ng thă
ng vuông go
c vơ
i mô
t trong hai đươ
ng thă
ng song song thı
vuông go
c vơ
i
đươ
ng thă
ng kia.
Câu 15: Cho hı
nh cho
p
SABC
co
SA
vuông go
c vơ
i mă
t phă
ng
(
)
ABC
va
đa
y
ABC
la
tam gia
c cân
ta
i
C
. Go
i
H
va
K
lâ
n lươ
t la
trung điê
m cu
a
AB
va
SB
. Trong ca
c khă
ng đi nh sau, khă
ng
đi nh na
o sai?
A.
⊥
CH SB
. B.
⊥
AK BC
. C.
⊥
CH SA
. D.
⊥
CH AK
.
Câu 16: Tính giới
hạn
2
2
1
lim
2 1
n
n n
+
+ +
?
A.
2
2
1
lim 0
2 1
n
n n
+
=
+ +
B.
2
2
1 1
lim
2 1 2
n
n n
+
=
+ +
C.
2
2
1
lim
2 1
n
n n
+
= +∞
+ +
D.
2
2
1
lim 1
2 1
n
n n
+
=
+ +
Câu 17: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác cân tại
B
, cạnh bên
SA
vuông góc với đáy,
I
l
à trung điểm
AC
,
H
là hình chiếu của
I
lên
SC
. Khẳng định nào sau đây đúng?
A.
(
)
(
)
BIH SBC
⊥ . B.
(
)
(
)
SAC SAB
⊥ .
C.
(
)
(
)
SBC ABC
⊥ . D.
(
)
(
)
SAC SBC
⊥ .
Câu 18: Cho hàm số
( ) ( )
3 2
3 2
3 2
mx mx
f x m x
= − + − −
. Tìm
m
để
(
)
0
f x
>
với mọi
x
A.
12
0
5
m< < . B.
0
m
<
. C.
12
5
m
<
D.
12
0
5
m≤ < .
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 3/22 Mã đề 483
Câu 19: Tính đạo hàm của hàm số
(
)
2017
3 2
3y x x= −
A.
(
)
2016
3 2
' 2017 3y x x= − . B.
(
)
(
)
2016
3 2 2
' 2017 3 3
y x x x x
= − − .
C.
(
)
(
)
2016
3 2 2
' 6051 3 2
y x x x x
= − − . D.
(
)
(
)
3 2 2
' 2017 3 3 6
y x x x x
= − − .
Câu 20: Tính giới hạn
2
2
2
lim
2 5 2
x
x
x x
→−
+
+ +
?
A.
2
2
2 1
lim
2 5 2 3
x
x
x x
→−
+
= −
+ +
. B.
2
2
2
lim 0
2 5 2
x
x
x x
→−
+
=
+ +
.
C.
2
2
2 1
lim
2 5 2 2
x
x
x x
→−
+
= −
+ +
. D.
2
2
2 1
lim
2 5 2 2
x
x
x x
→−
+
=
+ +
.
Câu 21: Cho tứ diện
ABCD
. Gọi
,
M N
là trung điểm của
,
AD BC
. Khẳng định nào sau đây đúng ?
A. Các vectơ , ,
AB AC MN
không đồng phẳng. B. Các vectơ , ,
DN AC MN
đồng phẳng.
C. Các vectơ ,
,
AB DC MN
đồng phẳng. D. Các vectơ , ,
AN CM MN
đồng phẳng.
Câu 22: Trong các dãy số sau, dãy số nào có giới hạn khác
0
?
A.
2 1
.
n
n
u
n
−
= B.
( )
1
.
1
n
u
n n
=
+
C.
1
.
3
n
n
u
=
D.
2
1
.
1
n
u
n
=
+
Câu 23: Cho cấp số cộng
(
)
n
u
có công sai
d
, tìm điều kiện của
d
để
(
)
n
u
là dãy số tăng
A.
0.
d
<
B.
1.
d
>
C.
0.
d
>
D.
1.
d
≥
Câu 24: Cho hàm số
( )
2
4
x
f x
x x
+
=
−
. Chọn khẳng định sai trong các khẳng định sau ?
A. Hàm số xác định trên
(
)
(
)
;0 0; 4
−∞ ∪ .
B. Hàm số liên tục tại
2.
x
=
C. Hàm số không liên tục tại
0
x
=
và
4.
x
=
D. Vì
( )
1
1
5
f − = −
;
(
)
2 2
f = nên
( )
(
)
1 . 2 0
f f
− <
, suy ra phương trình
(
)
0
f x
=
có ít
nhất 1 nghiệm thuộc
(
)
1;2
− .
Câu 25: Cho hình chóp
.
S ABCD
với đáy
ABCD
là hình thang vuông tại
A
và
D
, có
AD CD a
= =
,
2
AB a
=
,
(
)
SA ABCD
⊥ ,
E
là trung điểm của
AB
. Khẳng định nào sau đây đúng ?
A.
(
)
CE SDC
⊥ . B.
(
)
CB SAB
⊥ .
C.
SCD
∆
vuông ở
C
. D.
(
)
.
CE SAB
⊥
Câu 26: Xét các mệnh đề sau:
(
1) Nếu hàm số
(
)
f x
có đạo hàm tại điểm
0
x x
=
thì
(
)
f x
liên tục tại điểm đó.
(2) Nếu hàm số
(
)
f x
liên tục tại điểm
0
x x
=
thì
(
)
f x
có đạo hàm tại điểm đó.
(3) Nếu
(
)
f x
không liên tục tại
0
x x
=
thì chắc chắn
(
)
f x
không có đạo hàm tại điểm đó.
(4)
(
)
f x
có đạo hàm tại
0
x
khi và chỉ khi
(
)
f x
liên tục tại
0
x
.
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?
A.
2
. B.
1
. C.
4
. D.
3
.
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 4/22 Mã đề 483
Câu 27: Cho hàm số
( )
3 2
1
2 5 1
3
f x x x x
= − − +
. Giải phương trình
(
)
0
f x
′
=
.
A.
{
}
1; 5
− . B. vô nghiệm. C.
{
}
1; 5
−
. D.
{
}
2 5
±
.
Câu 28: Gọi
G
là trọng tâm của tứ diện
ABCD
. Trong các khẳng định sau, khẳng định nào sai?
A.
(
)
1
4
AG AB AC AD
= + +
. B.
(
)
2
3
AG AB AC AD
= + +
.
C.
0
GA GB GC GD
+ + + =
. D.
(
)
1
4
OG OA OB OC OD
= + + +
 
.
Câu 29: Tính giới hạn
2
lim
2
x
x x x
x
→−∞
+ +
+
?
A.
2
lim
2
x
x x x
x
→−∞
+ +
= −∞
+
. B.
2
lim 2
2
x
x x x
x
→−∞
+ +
= −
+
.
C.
2
lim 0
2
x
x x x
x
→−∞
+ +
=
+
. D.
2
lim 2
2
x
x x x
x
→−∞
+ +
=
+
.
Câu 30: Cho cấp số cộng
(
)
n
u
thỏa mãn
1 3
5
6
10
u u
u
− =
= −
, tìm số hạng tổng quát của cấp số cộng đó?
A.
5 3
n
u n
= −
. B.
5
n
u n
=
. C.
2 3
n
u n
= −
. D.
5 3
n
u n
= +
.
Câu 31: Cho ha
m sô
( )
2
2
x
f x
x
=
. Cho
n khă
ng đi nh đu
ng trong ca
c khă
ng đi nh sau.
A. Vı
(
)
(
)
0 0
lim lim
x x
f x f x
+ −
→ →
= nên
(
)
f x
liên tu
c ta
i
0
x
=
.
B. Ha
m sô
(
)
f x
xa
c đi nh vơ
i mo
i
0
x
≠
.
C.
(
)
(
)
0 0
lim lim
x x
f x f x
− +
→ →
≠ .
D. Ha
m sô
(
)
f x
liên tu
c trên
ℝ
.
Câu 32: Tı
m
m
đê
phương trı
nh
(
)
0
f x
′
=
co
nghiê
m. Biê
t
(
)
cos 2 sin 3 1
f x m x x x
= + − +
A.
0
m
>
. B.
5
m ≥ .
C.
0
m
<
. D.
5 5
m− < < .
Câu 33: Tı
nh giơ
i ha
n
( )
2
3
2 5
lim
3
x
x x
x
−
→ −
− +
+
A.
( )
2
3
2 5
lim
3
x
x x
x
−
→ −
− +
= +∞
+
. B.
( )
2
3
2 5
lim 2
3
x
x x
x
−
→ −
− +
=
+
.
C.
( )
2
3
2 5
lim
3
x
x x
x
−
→ −
− +
= −∞
+
. D.
( )
2
3
2 5
lim 2
3
x
x x
x
−
→ −
− +
= −
+
.
Câu 34: Tı
nh đa
o ha
m cu
a ha
m sô
(
)
1 2
1
x x
y
x
+
=
−
A.
( )
2
2
1 6
1
x
x
−
−
. B.
( )
2
4 1
1
x
x
+
−
. C.
( )
2
2
6 2 1
1
x x
x
− + +
−
. D.
( )
2
2
2 4 1
1
x x
x
− + +
−
.
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 5/22 Mã đề 483
Câu 35: Tı
nh đa
o ha
m cu
a ha
m sô
2
3 4 5
y x x
= − +
A.
2
6 4
3 4 5
x
x x
−
− +
. B.
2
3 1
3 4 5
x
x x
−
− +
. C.
2
1
2 3 4 5
x x
− +
. D.
2
3 2
3 4 5
x
x x
−
− +
.
Câu 36: Một viên đạn được bắn lên trời từ một vị trí cách mặt đất
1000
m
theo phương thẳng đứng với
vận tốc ban đầu
294 /
o
v m s
= (bỏ qua sức cản của không khí). Hỏi khi viên đạn đạt độ cao lớn
nhất và sẽ bắt đầu rơi thì viên đạn cách mặt đất bao nhiêu mét?
A.
4307, 5
. B.
5410
m
. C.
4410
m
. D.
4062,5
m
.
Câu 37: Chọn mệnh đề sai trong các mệnh đề sau?
A. Hàm số
3 2
2 10 3 2017
y x x x= − + + liên tục tại mọi điểm
x
∈
ℝ
.
B. Hàm số
2
1
1
y
x x
=
+ +
liên tục tại mọi điểm
x
∈
ℝ
.
C. Hàm số
3
1
1
y
x
=
+
liên tục tại mọi điểm
1
x
≠ −
.
D. Hàm số
2
x
y
x
=
−
liên tục tại mọi điểm
2
x
≠
.
Câu 38: Cho hình chóp .
S ABC
có đáy
ABC
là tam giác cân tại
A
, cạnh bên
SA
vuông góc với đáy,
M
là trung điểm
BC
,
J
là trung điểm
BM
. Khẳng định nào sau đây đúng?
A.
(
)
BC SAC
⊥ . B.
(
)
BC SAJ
⊥ .
C.
(
)
BC SAM
⊥ . D.
(
)
BC SAB
⊥ .
Câu 39: Cho tam giác
ABC
có ba góc
, ,
A B C
theo thứ tự lập thành một cấp số nhân với công bội
2
q
=
. Tính số đo góc
?
A
A.
2
π
. B.
7
π
. C.
2
7
π
. D.
4
7
π
.
Câu 40: Cho tứ diện đều
ABCD
. Gọi
ϕ
là góc giữa hai mặt phẳng
(BCD)
và
( )
ABC
. Khẳng định nào
sau đây là đúng:
A.
1
tan
3
ϕ =
. B.
0
60
ϕ = . C.
1
cos
3
ϕ =
. D.
0
30
ϕ = .
Câu 41: Tính tổng 10 số hạng đầu tiên của cấp số nhân
(
)
n
u
, biết
1
3
u
= −
và công bội
2.
q
= −
A.
10
1023.
S = − B.
10
1025.
S =
C.
10
1025.
S = − D.
10
1023.
S =
Câu 42: Viết phương trình tiếp tuyến của đồ thị hàm số
(
)
3 2
2
f x x x
= − +
, biết tiếp tuyến song song
với đường thẳng
5 5.
y x
= +
A.
121
5 ; 5 5.
27
y x y x
= − = +
B.
121
5 .
27
y x= +
C.
5 5.
y x
= −
D.
121
5 .
27
y x= −
Câu 43: Trong các dãy số
(
)
n
u
sau, hãy chọn dãy số tăng.
A.
.
n
u n
= −
B.
1
.
n
u
n
=
C.
( )
1 .
n
n
u n
= − D.
.
n
u n
=
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 6/22 Mã đề 483
Câu 44: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
Câu 45: Cho dãy số
(
)
n
u
xác định bởi công thức số hạng tổng quát
2
2 3
n
n
u
n
−
= với
1
n
≥
, tìm số hạng
thứ ba của dãy số.
A.
3
5.
u
=
B.
3
15.
u = C.
3
4.
u
=
D.
3
3.
u
=
Câu 46: Tính đạo hàm của hàm số:
tan 2
y x x
=
A.
2
2
tan 2
cos
x
x
x
+ . B.
2
tan 2
cos 2
x
x
x
+ .
C.
2
2 tan 2 tan 2 2
x x x x
+ +
. D.
2
2
cos 2
x
x
.
Câu 47: Cho hình chóp .
S ABC
có
( )
SA ABC
⊥
và tam giác
ABC
không vuông. Gọi
,
H K
lần lượt là
trực tâm các tam giác
ABC
và tam giác
SBC
. Khẳng định nào sau đây đúng?
A.
, ,
AH SK CB
đồng phẳng. B.
, ,
AH SK CB
đồng quy.
C.
, ,
AH SK CB
đôi một chéo nhau. D.
, ,
AH SK CB
đôi một song song.
Câu 48: Cho tứ
diện
ABCD
có
AB CD a
= =
,
3
2
a
IJ = . Gọi
,
I J
lần lượt là trung điểm của
BC
và
AD
. Tính số đo góc giữa hai đường thẳng
AB
và
CD
A.
0
90
. B.
0
45
. C.
0
60
. D.
0
30
.
Câu 49: Cho hình chóp
SABCD
có
ABCD
là hình thoi tâm
O
và
,
SA SC SB SD
= =
. Trong các khẳng
định sau khẳng định nào sai?
A.
AC SA
⊥
. B.
SA BD
⊥
. C.
AC BD
⊥
. D.
SD AC
⊥
.
Câu 50: Cho cấp
số nhân
( )
n
u
với
1
1
2
u
= −
,
7
32
u
= −
.Tìm công bội
q
của cấp số nhân trên?
A.
1
q
= ±
. B.
4
q
= ±
. C.
1
2
q
= ±
. D.
2
q
= ±
.
---- Hết ----
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 7/22 Mã đề 483
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C
D
B
A
C
D
A
A
A
C
C
C
A
D
B
B
A
D
C
A
C
A
C
D
D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
A
B
B
A
B
B
C
D
D
B
D
C
C
C
D
D
D
B
A
C
B
C
A
D
HƯƠ
NG DÂ
N GIA
I
Câu 1: Viết phương trình tiếp tuyến của đồ thị hàm số
3 2
( ) 2 3 1
f x x x x
= − + +
tại điểm có hoành độ
0
2
x
=
.
A.
7
y x
= − −
B.
y x
= −
C.
7 7
y x
= −
D.
9
y x
= − +
Hướng dẫn giải
Chọn C.
Với
0 0
2 7
x y
= ⇒ =
T
a có
2
( ) 3 4 3 (2) 7
f x x x f
′ ′
= − + ⇒ =
Vậy PTTT cần tìm là
(
)
(2) 2 7 7 7
y f x x
′
= − + = −
Câu 2: Tính giới hạn
→
+ −
x 0
1 x 1
lim ?
x
A.
→
+ −
= −
x 0
1 x 1 1
lim
x 2
. B.
→
+ −
= +∞
x 0
1 x 1
lim
x
. C.
→
+ −
=
x 0
1 x 1
lim 0
x
. D.
→
+ −
=
x 0
1 x 1 1
lim
x 2
.
Hướng dẫn giải:
Chọn D.
(
)
(
)
( ) ( )
→ → → →
+ − + +
+ −
= = = =
+ +
+ + + +
x 0 x 0 x 0 x 0
1 x 1 1 x 1
1 x 1 x 1 1
lim lim lim lim
x 2
1 x 1
x 1 x 1 x 1 x 1
Câu 3: Cho hàm số:
(
)
3
f x x
= +
. Tính
(
)
(
)
1 4 1
f f
′
+ .
A.
1
. B.
3
. C.
1
4
. D.
0
.
Hướng dẫn giải
Chọn B.
Ta có
( ) ( )
1
3
2 3
f x x f x
x
′
= + ⇒ =
+
Nên
( ) ( )
4
1 4 1 3 1 3
2 3 1
f f
′
+ = + + =
+
Câu 4: Cho hàm số:
3 2
( ) 3 4.
f x x x
= − +
Tính
(1).
f
′
A.
3
−
. B.
0
. C.
9
. D.
3
.
Hướng dẫn giải
Chọn A.
Ta có
2
( ) 3 6 (1) 3 6 3.
f x x x f
′ ′
= − ⇒ = − = −
Câu 5: Cho dãy số
(
)
n
u
với
( )
1 sin
n
n
u
n
π
= − , chọn khẳng định đúng trong các khẳng định sau?
A. Dãy số
(
)
n
u
là dãy số tăng.
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 8/22 Mã đề 483
B. Dãy số
(
)
n
u
bị chặn dưới nhưng không bị chặn trên.
C. Dãy số
(
)
n
u
bị chặn.
D. Dãy số
(
)
n
u
bị chặn trên nhưng không bị chặn dưới.
Hướng dẫn giải
Chọn C.
Ta có:
( )
1 sin sin 1
n
n
u
n n
π π
= − = ≤
. Vì vậy dãy số
(
)
n
u
là dãy bị chặn.
Câu 6: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
A
,
AB a
=
,
SA SB SC
= =
. Góc
giữa đường thẳng
SA
và mặt phẳng
(
)
ABC
bằng
0
45
. Tính theo
a
khoảng cách từ điểm
S
đến mặt phẳng
(
)
ABC
.
A.
3
3
a
. B.
3
a
. C.
2
a
. D.
2
2
a
.
Hướng dẫn giải
Chọn D.
Gọi
H
là hình chiếu của
S
trên
(
)
ABC
.
(
)
SH ABC
⇒ ⊥
(
)
(
)
;
SH d S ABC
⇒ = .
Ta có
SHA SHB SHC
∆ = ∆ = ∆
HA HB HC
⇒ = =
H
⇒
là tâm đường tròn ngoại tiếp
tam giác
ABC
.
Mặt khác
ABC
∆
vuông tại
A
nên
H
là trung điểm
của
BC
.
Do
(
)
SH ABC
⊥
( )
(
)
( )
0
; ; 45
SA ABC SA AH SAH⇒ = = = .
1 2
2 2
a
SH AH BC⇒ = = = .
Câu 7: Cho hàm số
(
)
4 2
2 1
f x x x
= − +
. Tìm
x
để
(
)
0
f x
′
>
A.
(
)
(
)
1;0 1;x
∈ − ∪ +∞
. B.
(
)
1;1
x ∈ − .
C.
(
)
(
)
; 1 0;1
x ∈ −∞ − ∪ . D.
x
∈
ℝ
.
Hướng dẫn giải.
Chọn A.
Ta có
( )
(
)
3 2
4 4 4 1
f x x x x x
′
= − = −
.
( )
(
)
2
0 4 1 0
f x x x
′
> ⇔ − >
.
Lập bảng xét dấu:
S
A
C
B
H
0
45
a
x
−∞
1
−
0
1
+∞
4
x
−
|
−
0
+
|
+
2
1
x
−
+
0
−
|
−
0
+
(
)
f x
′
−
0
+
0
−
0
+
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 9/22 Mã đề 483
Từ bảng xét dấu suy ra:
(
)
(
)
(
)
0 1;0 1;f x x
′
> ⇔ ∈ − ∪ +∞
.
Câu 8: Tìm tất cả các giá trị của
x
để ba số
2
1 , ,1
x x x
− +
theo thứ tự lập thành cấp số cộng?
A.
1
x
= ±
. B.
2
x
= ±
. C.
1
x
=
. D.
1
x
= −
.
Hướng dẫn giải.
Chọn A.
Cách 1:
Ta có ba số
2
1 , ,1
x x x
− +
theo thứ tự lập thành cấp số cộng
2
1 1 2
x x x
⇔ − + + =
1
x
⇔ = ±
.
Cách 2: Thử giá trị trong đáp án:
Với
1
x
=
thì ba số là
0;1;2
lập thành CSC nên thoả mãn.
Với
1
x
= −
thì ba số là
2;1;0
lập thành CSC nên thoả mãn.
Vậy chọn A.
Câu 9: Trong các dãy số sau, dãy số nào không là cấp số cộng?
A.
1 1 1 1 1
; ; ; ;
2 4 6 8 10
. B.
1 3 5 7 9
; ; ; ;
2 2 2 2 2
. C.
8; 6; 4; 2;0
− − − −
. D.
2; 2; 2; 2; 2
.
Hướng dẫn giải.
Chọn A.
Kiểm tra từng đáp án tính chất
1n n
a a d
+
− =
với
d
không đổi với
n
∀
.
Với đáp án A:
1 1 1 1
4 2 6 4
− ≠ −
nên dãy số ở đáp án A không là CSC
Các đáp án khác đều thoả mãn.
Câu 10: Tính đạo
hàm của hàm số
2sin 3 cos 2
y x x
= +
.
A.
2cos3 sin 2
y x x
′
= −
. B.
2cos3 sin 2
y x x
′
= +
.
C.
6cos3 2sin 2
y x x
′
= −
. D.
6cos3 2sin 2
y x x
′
= − +
.
Hướng dẫn giải.
Chọn C
Ta có
( ) ( ) ( ) ( )
2 sin 3 cos 2 2cos3 . 3 sin 2 . 2
y x x x x x x
′ ′ ′ ′
′
= + = −
6cos 3 2sin 2
x x
= −
.
Câu 11: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Hình chiếu vuông góc của
S
lên
(
)
ABC
trùng với trung điểm
H
của cạnh
BC
. Biết tam giác
SBC
là tam giác đều. Tính số đo
của góc giữa
SA
và
(
)
ABC
A.
30
°
. B.
45
°
. C.
60
°
. D.
90
°
.
Hướng dẫn giải
Chọn C.
SA
có hình chiếu lên
(
)
ABC
là
HA
.
Vậy góc giữa
SA
và
(
)
ABC
là
SAH
.
3
an
2
t
1
3
2
a
AH
SAH
SH
a
= = =
.
Vậy góc giữa
SA
và
(
)
ABC
có số đo là
45
°
.
S
B
C
H
A
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 10/22 Mã đề 483
Câu 12: Tính giới hạn
(
)
2
lim
− −
n n n
?
A.
(
)
2
lim
− − = +∞
n n n . B.
(
)
2
lim 1
− − = −
n n n .
C.
(
)
2
1
lim
2
− − = −
n n n . D.
(
)
2
lim 0
− − =
n n n .
Hướng dẫn giải.
Chọn C
(
)
( )
2
2
1 1
lim lim lim
2
1
1 1
− −
− − = = = −
− +
− +
n
n n n
n n n
n
Câu 13: Cho hı
nh lăng tru
.
′ ′ ′
ABC A B C
co
tâ
t ca
ca
c ca
nh đê
u bă
ng
a
. Go
c ta
o bơ
i ca
nh bên va
mă
t
phă
ng đa
y bă
ng
30
°
. Hı
nh chiê
u
H
cu
a
′
A
lên mă
t phă
ng
(
)
ABC
thuô
c đươ
ng thă
ng
BC
.
Tı
nh khoa
ng ca
ch tư
B
đê
n mă
t phă
ng
(
)
′ ′
ACC A
A.
21
7
a
. B.
3
4
a
. C.
3
2
a
. D.
21
14
a
.
Hướng dẫn giải.
Chọn A
Ta co
30
′
= °
A AH
do đo
3
.cos30
2
= ° =
a
AH a va
3 1
.
2 2
3
′
= =
a a
A H
. Go
i
K
la
hı
nh chiê
u cu
a
H
lên
AC
va
I
la
hı
nh chiê
u cu
a
H
lên
′
A K
.
Do tam gia
c
ABC
đê
u ca
nh bă
ng
a
nên
H
thuô
c đoa
n
BC
va
H
la
trung điê
m
BC
.
(
)
(
)
(
)
(
)
, 2 , 2
′ ′ ′ ′
= =
d ACC A d H ACC A HI
B .
1 3 3
2 2 4
= =
a a
HK nên
2
2 2 2 2 2
3 3
.
. 21
2 4 4
2 2 2
7
3 7
4 16 16
′
= = = =
′
+
+
a a a
HA HK a
HI
HA HK a a a
.
Câu 14: Trong ca
c mê
nh đê
sau, mê
nh đê
na
o đu
ng?
A. Hai đươ
ng thă
ng cu
ng vuông go
c vơ
i mô
t đươ
ng thă
ng thı
song song vơ
i nhau.
B. Hai đươ
ng thă
ng cu
ng vuông go
c vơ
i mô
t đươ
ng thă
ng thı
vuông go
c vơ
i nhau.
C. Mô
t đươ
ng thă
ng vuông go
c vơ
i mô
t trong hai đươ
ng thă
ng vuông go
c thı
song song vơ
i
đươ
ng thă
ng co
n la
i.
D. Mô
t đươ
ng thă
ng vuông go
c vơ
i mô
t trong hai đươ
ng thă
ng song song thı
vuông go
c vơ
i
đươ
ng thă
ng kia.
Hư
ớng dẫn giải.
Chọn D.
Tı
nh châ
t cơ ba
n trong SGK hı
nh ho
c 11.
C'
B'
H
A
C
B
A'
K
I
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 11/22 Mã đề 483
Câu 15: Cho hı
nh cho
p
SABC
co
SA
vuông go
c vơ
i mă
t phă
ng
(
)
ABC
va
đa
y
ABC
la
tam gia
c cân
ta
i
C
. Go
i
H
va
K
lâ
n lươ
t la
trung điê
m cu
a
AB
va
SB
. Trong ca
c khă
ng đi nh sau, khă
ng
đi nh na
o sai?
A.
⊥
CH SB
. B.
⊥
AK BC
. C.
⊥
CH SA
. D.
⊥
CH AK
.
Hướng dẫn giải.
Chọn B.
Ta co
(
)
⊥
CH SAB
nên
⊥
CH SB
suy ra A đu
ng va
⊥
CH AK
nên D đu
ng
Do
(
)
⊥
SA ABC
nên C đu
ng. Vâ
y cho
n B.
Câu 16: Tính giới hạn
2
2
1
lim
2 1
n
n n
+
+ +
?
A.
2
2
1
lim 0
2 1
n
n n
+
=
+ +
B.
2
2
1 1
lim
2 1 2
n
n n
+
=
+ +
C.
2
2
1
lim
2 1
n
n n
+
= +∞
+ +
D.
2
2
1
lim 1
2 1
n
n n
+
=
+ +
Hướng dẫn giải
Chọn B.
Vì:
2
2
2
2
1
1
1 1
lim lim
1 1
2 1 2
2
n
n
n n
n n
+
+
= =
+ +
+ +
Câu 17: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác cân tại
B
, cạnh bên
SA
vuông góc với đáy,
I
là trung điểm
AC
,
H
là hình chiếu của
I
lên
SC
. Khẳng định nào sau đây đúng?
A.
(
)
(
)
BIH SBC
⊥ . B.
(
)
(
)
SAC SAB
⊥ . C.
(
)
(
)
SBC ABC
⊥ . D.
(
)
(
)
SAC SBC
⊥ .
Hướng dẫn giải
Chọn A.
Vì
( ) ( ) ( )
BI SA
BI SAC BIH SAC
BI AC
⊥
⇒ ⊥ ⇒ ⊥
⊥
Câu 18: Cho hàm số
( ) ( )
3 2
3 2
3 2
mx mx
f x m x
= − + − −
. Tìm
m
để
(
)
0
f x
>
với mọi
x
A.
12
0
5
m< < . B.
0
m
<
. C.
12
5
m
<
D.
12
0
5
m≤ < .
Hướng dẫn giải
Chọn D.
K
H
A
C
B
S
I
A
B
C
S
H
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 12/22 Mã đề 483
(
)
(
)
2
' 3
f x mx mx m
= − + −
, để
(
)
0
f x
>
với mọi
x
thì
TH1:
0 3 0
m
= ⇒ >
đúng
TH2:
( )
2
2
0
0
12
0
4 3 0
5
5 12 0
m
m
m
m m m
m m
>
>
⇔ ⇔ < <
∆ = − − <
− <
Đáp số:
12
0
5
m≤ <
Câu 19: Tính đạo hàm của hàm số
(
)
2017
3 2
3y x x= −
A.
(
)
2016
3 2
' 2017 3y x x= − . B.
(
)
(
)
2016
3 2 2
' 2017 3 3
y x x x x
= − − .
C.
(
)
(
)
2016
3 2 2
' 6051 3 2
y x x x x
= − − . D.
(
)
(
)
3 2 2
' 2017 3 3 6
y x x x x
= − − .
Hướng dẫn giải
Chọn C.
(
)
(
)
(
)
(
)
2016 2016
3 2 2 3 2 2
' 2017 3 3 6 6051 3 2
y x x x x x x x x
= − − = − −
Câu 20: Tính giới hạn
2
2
2
lim
2 5 2
x
x
x x
→−
+
+ +
?
A.
2
2
2 1
lim
2 5 2 3
x
x
x x
→−
+
= −
+ +
. B.
2
2
2
lim 0
2 5 2
x
x
x x
→−
+
=
+ +
.
C.
2
2
2 1
lim
2 5 2 2
x
x
x x
→−
+
= −
+ +
. D.
2
2
2 1
lim
2 5 2 2
x
x
x x
→−
+
=
+ +
.
Hướng dẫn giải
Chọn A
( )( )
2
2 2 2
2 2 1 1
lim lim lim
2 5 2 2 2 1 2 1 3
x x x
x x
x x x x x
→− →− →−
+ + −
= = =
+ + + + +
Câu 21: Cho tứ diện
ABCD
. Gọi
,
M N
là trung điểm của
,
AD BC
. Khẳng định nào sau đây đúng ?
A. Các vectơ , ,
AB AC MN
không đồng phẳng.
B. Các vectơ ,
,
DN AC MN
đồng phẳng.
C. Các vectơ , ,
AB DC MN
đồng phẳng.
D. Các vectơ , ,
AN CM MN
đồng phẳng.
Hướng dẫn giải
Chọn C.
AB DC AM MN NB DM MN NC
+ = + + + + +

(
)
(
)
2
AM DM MN NB NC
= + + + +

V
ì
,
M N
là trung điểm của
,
AD BC
Nên :
0
0
AM DM
NB NC
+ =
+ =

Vậy
2
AB DC MN
+ =

.
Nên các vectơ , ,
AB DC MN
đồng phẳng
A
B
C
D
M
N
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 13/22 Mã đề 483
Câu 22: Trong các dãy số sau, dãy số nào có giới hạn khác
0
?
A.
2 1
.
n
n
u
n
−
= B.
( )
1
.
1
n
u
n n
=
+
C.
1
.
3
n
n
u
=
D.
2
1
.
1
n
u
n
=
+
Hướng dẫn giải
Chọn A.
1
2
2 1 2
2 0
1 1
n
n
lim lim
n
−
−
= = = ≠
Câu 23: Cho cấp số cộng
(
)
n
u
có công sai
d
, tìm điều kiện của
d
để
(
)
n
u
là dãy số tăng
A.
0.
d
<
B.
1.
d
>
C.
0.
d
>
D.
1.
d
≥
Hướng dẫn giải
Chọn C.
(
)
n
u
là dãy số tăng khi và chỉ khi
*
1
0,
n n
u u n N
+
− > ∀ ∈
(
)
(
)
1 1
1 0
u nd u n d
⇔ + − + − >
0
d
⇔ >
Câu 24: Cho hàm số
( )
2
4
x
f x
x x
+
=
−
. Chọn khẳng định sai trong các khẳng định sau ?
A. Hàm số xác định trên
(
)
(
)
;0 0; 4
−∞ ∪ .
B. Hàm số liên tục tại
2.
x
=
C. Hàm số không liên tục tại
0
x
=
và
4.
x
=
D. Vì
( )
1
1
5
f − = −
;
(
)
2 2
f = nên
( )
(
)
1 . 2 0
f f
− <
, suy ra phương trình
(
)
0
f x
=
có ít
nhất 1 nghiệm thuộc
(
)
1;2
− .
Hướng dẫn giải
Chọn D.
Tập xác định :
(
)
(
)
;0 0;4
D = −∞ ∪
Hay hàm số liên tục trên
(
)
;0
−∞ và
(
)
0; 4
. Từ đó suy ra hàm số không liên tục trên
[
]
1;2
− .
Vậy D sai.
Câu 25: Cho hình chóp
.
S ABCD
với đáy
ABCD
là hình thang vuông tại
A
và
D
, có
AD CD a
= =
,
2
AB a
=
,
(
)
SA ABCD
⊥ ,
E
là trung điểm của
AB
. Khẳng định nào sau đây đúng ?
A.
(
)
CE SDC
⊥ . B.
(
)
CB SAB
⊥
C.
SCD
∆
vuông ở
C
D.
(
)
.
CE SAB
⊥
Hướng dẫn giải
Chọn D.
Xét tứ giác
AECD
có :
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 14/22 Mã đề 483
/ /
90
AE CD
AE CD AD a
A
= = =
= °
Nên
AECD
là hình vuông.
Có :
( )
CE AB
CE SAB
CE SA
⊥
⇒ ⊥
⊥
.
Vậy D đúng.
Câu 26: Xét các mệnh đề sau:
(
1) Nếu hàm số
(
)
f x
có đạo hàm tại điểm
0
x x
=
thì
(
)
f x
liên tục tại điểm đó.
(2) Nếu hàm số
(
)
f x
liên tục tại điểm
0
x x
=
thì
(
)
f x
có đạo hàm tại điểm đó.
(3) Nếu
(
)
f x
không liên tục tại
0
x x
=
thì chắc chắn
(
)
f x
không có đạo hàm tại điểm đó.
(4)
(
)
f x
có đạo hàm tại
0
x
khi và chỉ khi
(
)
f x
liên tục tại
0
x
.
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?
A.
2
. B.
1
. C.
4
. D.
3
.
Hướng dẫn giải
Chọn A.
Theo định lý
1
thì (1) và (3) đúng.
Xét hàm số:
(
)
f x x
=
ta có:
(
)
0
lim 0
x
f x
+
→
=
và
(
)
0
lim 0
x
f x
−
→
=
nên hàm số liên tục tại
0
x
=
.
Mặt khác:
(
)
(
)
0
0
lim 1
0
x
f x f
x
+
→
−
=
−
và
(
)
(
)
0
0
lim 1
0
x
f x f
x
−
→
−
= −
−
nên hàm số không có đạo hàm tại
0
x
=
. Vậy (2) và (4) sai.
Câu 27: Cho hàm số
( )
3 2
1
2 5 1
3
f x x x x
= − − +
. Giải phương trình
(
)
0
f x
′
=
.
A.
{
}
1; 5
− . B. vô nghiệm. C.
{
}
1; 5
−
. D.
{
}
2 5
±
.
Hướng dẫn giải
Chọn A.
Ta có:
( )
2
4 5
f x x x
′
= − −
.
Do đó
(
)
0
f x
′
=
2
1
4 5 0
5
x
x x
x
= −
⇔ − − = ⇔
=
Câu 28: Gọi
G
là trọng tâm của tứ diện
ABCD
. Trong các khẳng định sau, khẳng định nào sai?
A.
(
)
1
4
AG AB AC AD
= + +
. B.
(
)
2
3
AG AB AC AD
= + +
.
C.
0
GA GB GC GD
+ + + =
. D.
(
)
1
4
OG OA OB OC OD
= + + +
 
.
Hướng dẫn giải
Chọn B.
Ta có:
0
GA GB GC GD AG GB GC GD
+ + + = ⇔ = + +

S
A
B
C
D
E
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 15/22 Mã đề 483
(
)
(
)
(
)
(
)
1
4
AG AB AG AC AG AD AG AG AB AC AD
⇔ = − + − + − ⇔ = + +
  
.
Câu 29: Tính giới hạn
2
lim
2
x
x x x
x
→−∞
+ +
+
?
A.
2
lim
2
x
x x x
x
→−∞
+ +
= −∞
+
. B.
2
lim 2
2
x
x x x
x
→−∞
+ +
= −
+
.
C.
2
lim 0
2
x
x x x
x
→−∞
+ +
=
+
. D.
2
lim 2
2
x
x x x
x
→−∞
+ +
=
+
.
Hướng dẫn giải
Chọn B.
2
1
1 1
1 1
1 1 1
lim lim lim lim 2
2
2 2
2
1
1 1
x x x x
x
x x
x
x x x
x x
x
x x
x
x x
→−∞ →−∞ →−∞ →−∞
− + +
+ + + +
+ +
= = = − = −
+
+
+ +
.
Câu 30: Cho cấp
số cộng
(
)
n
u
thỏa mãn
1 3
5
6
10
u u
u
− =
= −
, tìm số hạng tổng quát của cấp số cộng đó?
A.
5 3
n
u n
= −
. B.
5
n
u n
=
. C.
2 3
n
u n
= −
. D.
5 3
n
u n
= +
.
Hướng dẫn giải
Chọn A.
Gọi
1
u
là số hạng đầu và
d
là công sai của cấp số cộng. theo đề ta có hệ phương trình:
(
)
1 1
1
1
2 6
3
2
4 10
u u d
d
u
u d
− + =
= −
⇔
=
+ = −
Số hạng tổng quát:
(
)
(
)
(
)
1
1 2 1 3 5 3
n
u u n d n n
= + − = + − − = −
.
Câu 31: Cho ha
m sô
( )
2
2
x
f x
x
=
. Cho
n khă
ng đi nh đu
ng trong ca
c khă
ng đi nh sau.
A. Vı
(
)
(
)
0 0
lim lim
x x
f x f x
+ −
→ →
=
nên
(
)
f x
liên tu
c ta
i
0
x
=
.
B. Ha
m
sô
(
)
f x
xa
c đi nh vơ
i mo
i
0
x
≠
.
C.
(
)
(
)
0 0
lim lim
x x
f x f x
− +
→ →
≠ .
D. Ha
m sô
(
)
f x
liên tu
c trên
ℝ
.
Hươ
ng dân gia
i
Cho
n B.
2
0 0
2
lim lim 2 0
x x
x
x
x
+ +
→ →
= =
;
(
)
0 0
lim lim 2 0
x x
f x x
− −
→ →
= =
(
)
(
)
0 0
lim lim
x x
f x f x
+ −
→ →
= nên
(
)
f x
liên tu
c ta
i
0
x
=
.
Hàm số
( )
2
2
x
f x
x
= không xác định tại
0
x
=
.
Với mọi
0
x
≠
hàm số
( )
2
2
2
x
f x x
x
= =
.
Câu 32: Tı
m
m
đê
phương trı
nh
(
)
0
f x
′
=
co
nghiê
m. Biê
t
(
)
cos 2sin 3 1
f x m x x x
= + − +
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 16/22 Mã đề 483
A.
0
m
>
. B.
5
m ≥ . C.
0
m
<
. D.
5 5
m− < < .
Hươ
ng dân gia
i
Chọn B.
(
)
sin 2cos 3
f x m x x
′
= − + −
(
)
0 sin 2 cos 3 0 sin 2 cos 3
f x m x x m x x
′
= ⇔ − + − = ⇔ − + =
(
)
∗
P
hương trình
(
)
∗
có nghiệm khi
( )
2
2 2 2
2 3 5 5
m m m− + ≥ ⇔ ≥ ⇔ ≥ .
Câu 33: Tı
nh giơ
i ha
n
( )
2
3
2 5
lim
3
x
x x
x
−
→ −
− +
+
A.
( )
2
3
2 5
lim
3
x
x x
x
−
→ −
− +
= +∞
+
. B.
( )
2
3
2 5
lim 2
3
x
x x
x
−
→ −
− +
=
+
.
C.
( )
2
3
2 5
lim
3
x
x x
x
−
→ −
− +
= −∞
+
. D.
( )
2
3
2 5
lim 2
3
x
x x
x
−
→ −
− +
= −
+
.
Hươ
ng dân gia
i
Chọn C
( )
(
)
2
3
lim 2 5 26 0
x
x x
−
→ −
− + = >
( )
(
)
3
lim 3 0
x
x
−
→ −
+ =
và
( )
3
x
−
→ −
thì
3 0
x
+ <
.
Suy ra
( )
2
3
2 5
lim
3
x
x x
x
−
→ −
− +
+
=
−∞
.
Câu 34: Tı
n
h đa
o ha
m cu
a ha
m sô
(
)
1 2
1
x x
y
x
+
=
−
A.
( )
2
2
1 6
1
x
x
−
−
. B.
( )
2
4 1
1
x
x
+
−
. C.
( )
2
2
6 2 1
1
x x
x
− + +
−
. D.
( )
2
2
2 4 1
1
x x
x
− + +
−
.
Hươ
ng dân gia
i
Chọn D.
(
)
2
1 2
2
1 1
x x
x x
y
x x
+
+
= =
− −
( )
( )
( )
( )
( )
( )( )
( )
( )
( ) ( )
2 2 2
2
2 2 2
2 1 2 1 1 4 1 2 1
2 4 1
1 1 1
x x x x x x x x x x
x x
y
x x x
′
′
+ − − + − + − − + −
− + +
′
= = =
− − −
.
Câu 35: Tı
nh đa
o ha
m cu
a ha
m sô
2
3 4 5
y x x
= − +
A.
2
6 4
3 4 5
x
x x
−
− +
. B.
2
3 1
3 4 5
x
x x
−
− +
. C.
2
1
2 3 4 5
x x
− +
. D.
2
3 2
3 4 5
x
x x
−
− +
.
Hươ
ng dân gia
i
Chọn D.
( )
2
2 2 2
3 4 5
6 4 3 2
2 3 4 5 2 3 4 5 3 4 5
x x
x x
y
x x x x x x
′
− +
− −
′
= = =
− + − + − +
.
y
(t=30)
(t=0)
5410
1000
O
A
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 17/22 Mã đề 483
Câu 36: Một viên đạn được bắn lên trời từ một vị trí cách mặt đất
1000
m
theo phương thẳng đứng với
vận tốc ban đầu
294 /
o
v m s
= (bỏ qua sức cản của không khí). Hỏi khi viên đạn đạt độ cao lớn
nhất và sẽ bắt đầu rơi thì viên đạn cách mặt đất bao nhiêu mét?
A.
4307,5
. B.
5410
m
. C.
4410
m
. D.
4062,5
m
.
Hươ
ng dân gia
i
Chọn B.
Chọn trục
Oy
theo phương thẳng đứng, chiều dương hướng từ mặt đất lên trời, gốc
O
ở mặt
đất và cách
A
là vị trí viên đạn được bắn lên, gốc thời gian (tức lúc
0
t
=
) được tính từ vị trí
A
như hình bên; khi đó chuyển động của viên đạn là chuyển động biến đổi đều với vận tốc ban
đầu
294 /
o
v m s
= và với gia tốc. (Gia tốc nhận giá trị âm vì véc tơ gia tốc ngược chiều dương
của trục
Oy
. Phương trình chuyển động của viên đạn là:
2
1000 294 4,9
y t t
= + −
Ta có
(
)
294 9,8
v t y t
′
= = −
Viên đạn đạt độ cao lớn nhất và sẽ bắt đầu rơi
(
)
(
)
0 294 9,8 0 30
v t t t s
= ⇔ − = ⇔ =
Khi đó viên đạn cách mặt đất là
(
)
(
)
2
30 1000 294.30 4,9.30 5410
y m
= + − =
Câu 37: Chọn mệnh đề sai trong các mệnh đề sau?
A. Hàm số
3 2
2 10 3 2017
y x x x= − + + liên tục tại mọi điểm
x
∈
ℝ
.
B. Hàm số
2
1
1
y
x x
=
+ +
liên tục tại mọi điểm
x
∈
ℝ
.
C. Hàm số
3
1
1
y
x
=
+
liên tục tại mọi điểm
1
x
≠ −
.
D. Hàm số
2
x
y
x
=
−
liên tục tại mọi điểm
2
x
≠
.
Hươ
ng dân gia
i
Chọn D
Mệnh đề A đúng vì hàm số
3 2
2 10 3 2017
y x x x= − + + là hàm đa thức có tập xác định
ℝ
nên
hàm số liên tục tại mọi điểm
x
∈
ℝ
.
Mệnh đề B đúng vì hàm số
2
1
1
y
x x
=
+ +
là hàm phân thức hữu tỉ, có tập xác định
ℝ
nên hàm
số liên tục tại mọi điểm
x
∈
ℝ
.
Mệnh đề C đúng vì hàm số
3
1
1
y
x
=
+
là hàm phân thức hữu tỉ, có tập xác định
{
}
\ 1
−
ℝ
nên
hàm số liên tục tại mọi điểm
1
x
≠ −
.
Mệnh đề D sai vì hàm số
2
x
y
x
=
−
có tập xác định
(
)
; 2
D = −∞ nên hàm số bị gián đoạn tại
các điểm
[
)
2;x
∈ + ∞
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 18/22 Mã đề 483
Câu 38: Cho hình chóp .
S ABC
có đáy
ABC
là tam giác cân tại
A
, cạnh bên
SA
vuông góc với đáy,
M
là trung điểm
BC
,
J
là trung điểm
BM
. Khẳng định nào sau đây đúng?
A.
(
)
BC SAC
⊥ . B.
(
)
BC SAJ
⊥ . C.
(
)
BC SAM
⊥ .
D.
(
)
BC SAB
⊥ .
Hươ
ng dân gia
i
Chọn C.
Tam giác
ABC
là tam giác cân tại
A
,
AM
là đường trung tuyến
đồng thời là đường cao nên
AM BC
⊥
Lại có
(
)
SA ABC
⊥ ,
(
)
BC ABC
⊂
SA BC
⇒ ⊥
Từ đó suy ra
(
)
BC SAM
⊥ .
Câu 39: Cho tam giác
ABC
có ba góc
, ,
A B C
theo thứ tự lập thành một cấp
số nhân với công bội
2
q
=
. Tính số đo góc
?
A
A.
2
π
. B.
7
π
. C.
2
7
π
. D.
4
7
π
.
Hươ
ng dân gia
i
Chọn C.
Theo giả thiết ta có
, ,
A B C
lập thành cấp số nhân với
2
q
=
nên
2 ; 4
B A C A
= =
Mà
ABC
là một tam giác nên 2 4
7
A A A A
π
π
+ + = ⇔ =
Câu 40: Cho tứ diện đều
ABCD
. Gọi
ϕ
là góc giữa hai mặt phẳng
(BCD)
và
( )
ABC
. Khẳng định nào
sau đây là đúng:
A.
1
tan
3
ϕ =
. B.
0
60
ϕ = . C.
1
cos
3
ϕ =
. D.
0
30
ϕ = .
Hươ
ng dân gia
i
Chọn C.
Giả sử tứ diện đều có tất cả các cạnh bằng
x
Gọi
M
là trung điểm
BC
Do tam giác
,
ABC DBC
đều nên
AM BC
DM BC
⊥
⊥
D
o đó:
( ; )
AM DM
ϕ
=
Xét tam giác
AMD
có:
3
2
x
AM DM= =
Nên
A
B
C
D
M
A
C
B
S
M
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 19/22 Mã đề 483
2 2
2 2
2 2 2
2
3 3 1
1
4 4 2
cos 0
3
2. . 3
3 3
2. .
2
2 2
x x
x x
AM MD AD
AMD
x
AM MD
x x
+ −
+ −
= = = = >
Nên
cos cos( ; ) cos
AMD AM MD
ϕ
= =
Vậy
1
cos
3
ϕ
=
.
Câu 41: Tính tổng 10 số hạng đầu tiên của cấp số nhân
(
)
n
u
, biết
1
3
u
= −
và công bội
2.
q
= −
A.
10
1023.
S = − B.
10
1025.
S = C.
10
1025.
S = − D.
10
1023.
S =
Hươ
ng dân gia
i
Cho
n D.
Ta có:
(
)
10
1
10
1
1023.
1
u q
S
q
−
= =
−
Câu 42: Viết phương trình tiếp tuyến của đồ thị hàm số
(
)
3 2
2
f x x x
= − +
, biết tiếp tuyến song song
với đường thẳng
5 5.
y x
= +
A.
121
5 ; 5 5.
27
y x y x
= − = +
B.
121
5 .
27
y x= +
C.
5 5.
y x
= −
D.
121
5 .
27
y x= −
Hươ
ng dân gia
i
Cho
n D.
+
(
)
2
3 2
f x x x
′
= −
, Gọi
0
x
là hoành độ tiếp điểm.
Vì tiếp tuyến song song với đường thẳng
5 5
y x
= +
nên
( )
0
2
0 0 0
0
1
5 3 2 5
5
3
x
f x x x
x
= −
′
= ⇔ − = ⇔
=
+ Với
0 0
1 0
x y
= − ⇒ =
, ta có pttt:
(
)
5 1 5 5
y x x
= + = +
(loại)
+ Với
0 0
5 104
3 27
x y= ⇒ = , ta có pttt:
5 104 121
5 5 .
3 27 27
y x x
= − + = −
Câu 43: Trong các dãy số
(
)
n
u
sau, hãy chọn dãy số tăng?
A.
.
n
u n
= −
B.
1
.
n
u
n
=
C.
( )
1 .
n
n
u n
= − D.
.
n
u n
=
Hư
ớng dẫn giải
Chọn D.
Ta có:
1
1
n n
u n u n
+
= ⇒ = +
Xét hiệu
(
)
*
1
1 1 0,
n n
u u n n n
+
− = + − = > ∀ ∈ ⇒
ℕ
Dãy số tăng.
Câu 44: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đư
ờng thẳng cùng vuông góc với một mặt phẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
C. Hai đư
ờng thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 20/22 Mã đề 483
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
Hướng dẫn giải
Chọn B.
Câu A sai vì: Hai đường thẳng cùng vuông góc với một mặt phẳng có thể trùng nhau.
Câu B đúng.
Câu C sai vì : Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng có thể chéo
nhau.
Câu D sai vì : Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng có thể cắt nhau.
Câu 45: Cho dãy số
(
)
n
u
xác định bởi công thức số hạng tổng quát
2
2 3
n
n
u
n
−
= với
1
n
≥
, tìm số hạng
thứ ba của dãy số.
A.
3
5.
u
=
B.
3
15.
u = C.
3
4.
u
=
D.
3
3.
u
=
Hướng dẫn giải
Chọn A.
Ta có:
2 2
3
2 3 2.3 3
5.
3
n
n
u u
n
− −
= ⇒ = =
Câu 46: Tính đạo hàm của hàm số:
tan 2
y x x
=
A.
2
2
tan 2
cos
x
x
x
+ . B.
2
tan 2
cos 2
x
x
x
+ .
C.
2
2 tan 2 tan 2 2
x x x x
+ +
. D.
2
2
cos 2
x
x
.
Hướng dẫn giải
Chọn C.
( ) ( )
tan 2 ) tan 2 tan 2
y x x y x x x x
′
′
= ⇒ = +
( )
2
2 2
2
2
tan 2 tan 2 2 tan 2 tan 2 2
cos 2 cos 2
x
x
x x x x x x x
x x
′
= + = + = + +
.
Câu 47: Cho hình chóp .
S ABC
có
( )
SA ABC
⊥
và tam giác
ABC
không vuông. Gọi
,
H K
lần lượt là
trực tâm các tam giác
ABC
và tam giác
SBC
. Khẳng định nào sau đây đúng?
A.
, ,
AH SK CB
đồng phẳng. B.
, ,
AH SK CB
đồng quy.
C.
, ,
AH SK CB
đôi một chéo nhau. D.
, ,
AH SK CB
đôi một song song.
Hướng dẫn giải
Chọn B
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 21/22 Mã đề 483
I
A
B
C
S
H
K
Trong
(
)
ABC
gọi
I
là giao điểm
AH
và
BC
( )
BC SA SA ABC
⊥ ⊥
và
BC AI
⊥
( Vì
H
là trực tâm tam giác
ABC
)
BC (SAI) BC SI
⇒ ⊥ ⇒ ⊥
Mà
BC SK
⊥
suy ra
SK
đi qua
I
Vậy
, ,
AH SK CB
đồng quy
Câu 48: Cho tứ diện
ABCD
có
AB CD a
= =
,
3
IJ
2
a
=
.Gọi
,
I J
lần lượt là trung điểm của
BC
v
à
AD
. Tính số đo góc giữa hai đường thẳng
AB
và
CD
A.
0
90
. B.
0
45
. C.
0
60
. D.
0
30
.
Hướng dẫn giải
Chọn C
B
D
C
A
I
J
N
M
Gọi
M
là trung điểm
AC
,
N
là trung điểm
DB
Ta có
1
/ / / / ,
2 2
a
IN CD JM IN JM CD
= = =
1
/ / / / ,
2 2
a
IM AB JN IM JN AB
= = =
2 2 2
0
3
cosMIJ MIJ 30
2 . 2
MI IJ MJ
MI IJ
+ −
= = ⇒ =
0
MIN 2MIJ 60
⇒ = =
(
MINJ
là hình thoi)
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 22/22 Mã đề 483
( ) ( )
0
6
,
0
,AB CD IM I MINN = ==
Câu 49: Cho hình chóp
SABCD
có
ABCD
là hình thoi tâm
O
và
,
SA SC SB SD
= =
. Trong các khẳng
định sau khẳng định nào sai?
A.
AC SA
⊥
. B.
SA BD
⊥
. C.
AC BD
⊥
. D.
SD AC
⊥
.
Hướng dẫn giải
Chọn A
O
A
B
C
D
S
Ta có:
( )
SO AC
SO BD
SO ABCD
⊥
⊥
⇒ ⊥
Từ đây ta chứng minh được
( )
AC SBD AC SD
⊥ ⇒ ⊥
Từ đây ta chứng minh được ( )
BD SAC BD SA
⊥ ⇒ ⊥
Câu C hiển nhiên đúng do ABCD là hình thoi
Câu 50: Cho cấp
số nhân
( )
n
u
với
= −
1
1
u
2
7
32
u
= −
.Tìm công bội
q
của cấp số nhân trên?
A.
1
q
= ±
. B.
4
q
= ±
. C.
1
2
q
= ±
. D.
2
q
= ±
.
Hướng dẫn giải
Chọn D
.
6 6 6
7 1
1
32 64 2
2
u u q q q q
−
= ⇔ − = ⇔ = ⇔ = ±
.
| 1/22

Tài liệu khác của Toán 11

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI HỌC KỲ 2 LỚP 11 NĂM HỌC 2016-2017
THPT CHUYÊN NGUYỄN HUỆ Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ và tên thí sinh: …………………………………………………………
Số báo danh:………………………………………………………………
Câu 1: Viết phương trình tiếp tuyến của đồ thị hàm số 3 2
f (x) = x − 2x + 3x +1 tại điểm có hoành độ x = 2 0
A. y = −x − 7 .
B. y = 7x −14 .
C. y = 7x − 7 .
D. y = −x + 9 . Câu 2: 1+ x −1 Tính giới hạn lim ? x→0 x A. 1 + x − 1 1 1 + x − 1 1 + x − 1 1 + x − 1 1 lim = − . B. lim = +∞ . C. lim = 0 . D. lim = . x→0 x 2 x→0 x x→0 x x→0 x 2
Câu 3: Cho hàm số: f ( x) = 3+ x . Tính f ( ) 1 + 4 f ′( ) 1 A. 1. B. 3 . C. 1 . D. 0 . 4
Câu 4: Cho hàm số: 3 2
f (x) = x − 3x + 4. Tính f ( ′ 1). A. 3 − . B. 0 . C. 9 . D. 3 . Câu 5: n π
Cho dãy số (u với u = −
, chọn khẳng định đúng trong các khẳng định sau? n ( ) 1 sin n ) n
A. Dãy số (u là dãy số tăng. n )
B. Dãy số (u bị chặn dưới nhưng không bị chặn trên. n )
C. Dãy số (u bị chặn. n )
D. Dãy số (u bị chặn trên nhưng không bị chặn dưới. n )
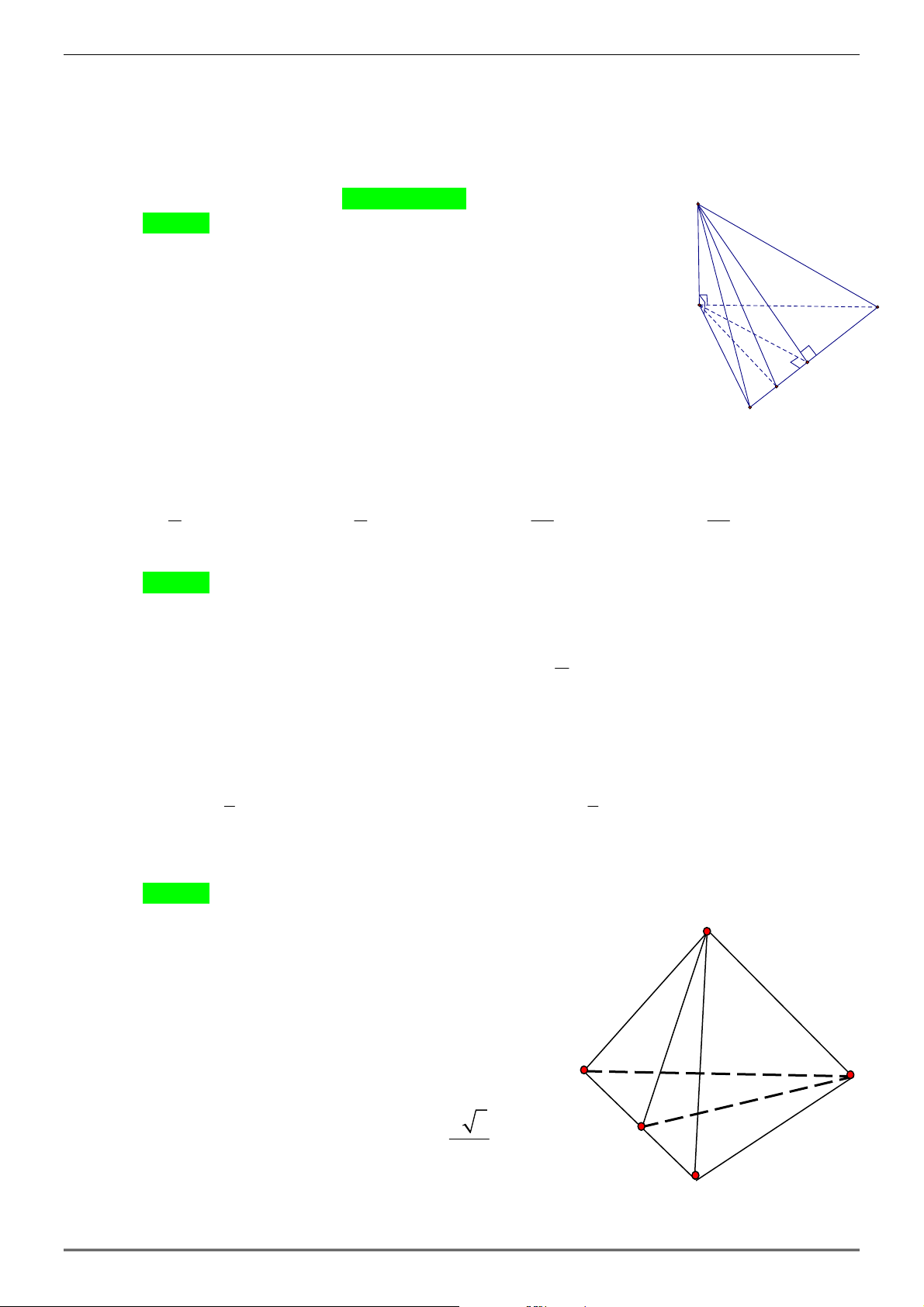
Câu 6: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , AB = a , SA = SB = SC .
Góc giữa đường thẳng SA và mặt phẳng ( ABC ) bằng 0
45 . Tính theo a khoảng cách từ điểm
S đến mặt phẳng ( ABC ) . A. a 3 a . B. a 3 . C. a 2 . D. 2 . 3 2
Câu 7: Cho hàm số f ( x) 4 2
= x − 2x +1. Tìm x để f ′( x) > 0 . A. x ∈( 1
− ; 0) ∪ (1; +∞) . B. x ∈( 1 − ; ) 1 .
C. x ∈(−∞;− ) 1 ∪ (0; )
1 .D. x ∈ ℝ .
Câu 8: Tìm tất cả các giá trị của x để ba số 2
1− x, x ,1+ x theo thứ tự lập thành cấp số cộng? A. x = 1 ± . B. x = 2 ± . C. x = 1. D. x = 1 − .
Câu 9: Trong các dãy số sau, dãy số nào không là cấp số cộng? A. 1 1 1 1 1 ; ; ; ; . B. 1 3 5 7 9 ; ; ; ; . C. 8 − ; −6; 4 − ; 2 − ;0 . D. 2; 2; 2; 2; 2 . 2 4 6 8 10 2 2 2 2 2
Câu 10: Tính đạo hàm của hàm số y = 2sin 3x + cos 2x
A. y′ = 2cos3x − sin 2x .
B y′ = 2 cos3x + sin 2x .
C. y′ = 6cos3x − 2sin 2x .
D. y′ = −6cos3x + 2sin 2x .
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 1/22 Mã đề 483
Câu 11: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông góc của S lên
( ABC ) trùng với trung điểm H của cạnh BC . Biết tam giác SBC là tam giác đều. Tính số đo
của góc giữa SA và ( ABC ) A. 30° . B. 45° . C. 60° . D. 90° .
Câu 12: Tính giới hạn ( 2 lim
n − n − n) ? A. ( 2 lim
n − n − n) = +∞ . B. ( 2 lim
n − n − n) = 1 − . C. lim( 1 2
n − n − n) = − . D. ( 2 lim
n − n − n) = 0. 2
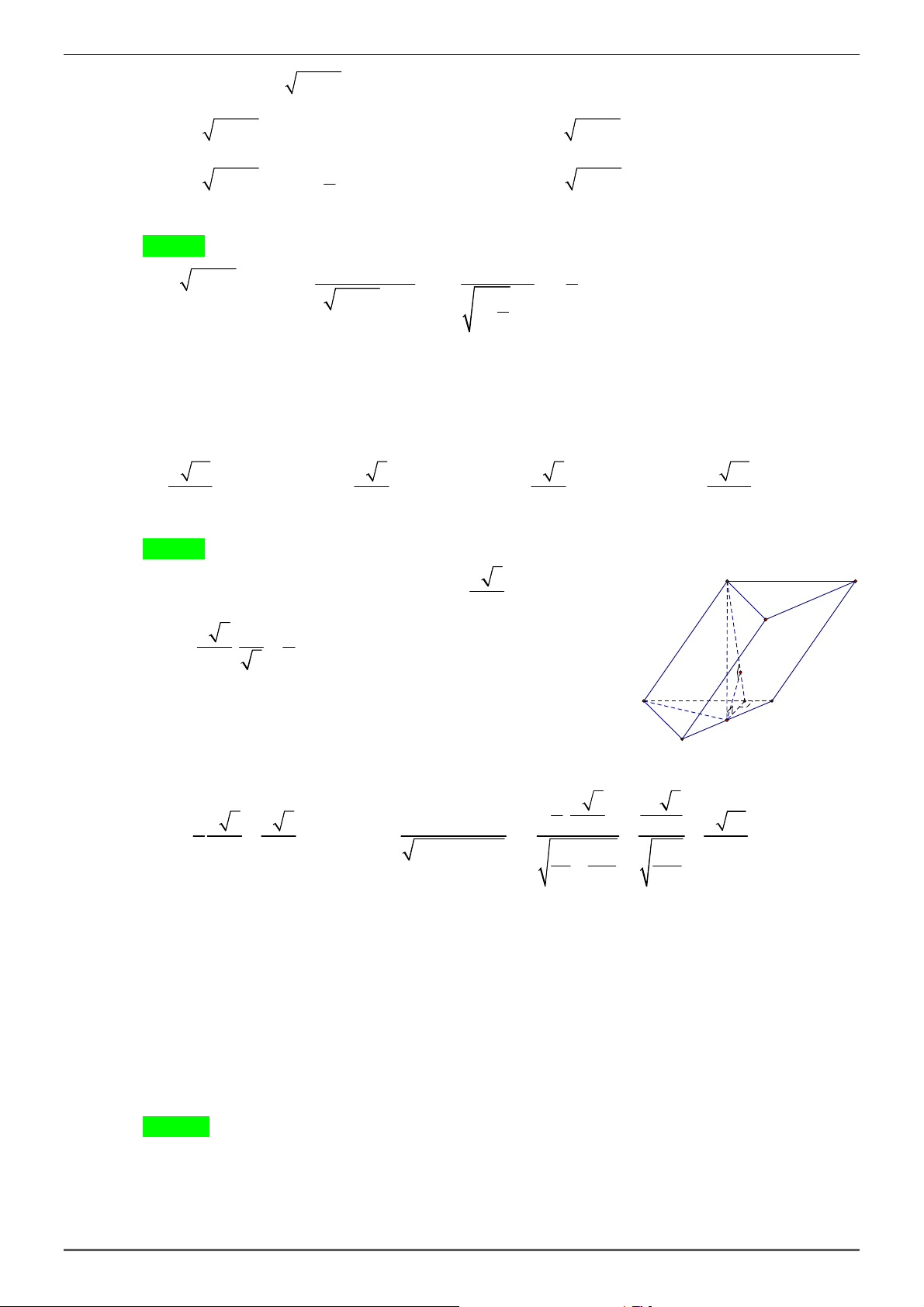
Câu 13: Cho hı̀nh lăng tru ̣ ABC. ′
A B′C′ có tất cả các ca ̣nh đều bằng a . Góc ta ̣o bởi ca ̣nh bên và mă ̣t
phẳng đáy bằng 30° . Hı̀nh chiếu H của ′
A lên mă ̣t phẳng ( ABC ) thuô ̣c đường thẳng BC .
Tı́nh khoảng cách từ B đến mă ̣t phẳng ( ACC′ ′ A ) A. a 21 a a a . B. 3 . C. 3 . D. 21 . 7 4 2 14
Câu 14: Trong các mê ̣nh đề sau, mê ̣nh đề nào đúng?
A. Hai đường thẳng cùng vuông góc với mô ̣t đường thẳng thı̀ song song với nhau.
B. Hai đường thẳng cùng vuông góc với mô ̣t đường thẳng thı̀ vuông góc với nhau.
C. Mô ̣t đường thẳng vuông góc với mô ̣t trong hai đường thẳng vuông góc thı̀ song song với
đường thẳng còn la ̣i.
D. Mô ̣t đường thẳng vuông góc với mô ̣t trong hai đường thẳng song song thı̀ vuông góc với đường thẳng kia.
Câu 15: Cho hı̀nh chóp SABC có SA vuông góc với mă ̣t phẳng ( ABC ) và đáy ABC là tam giác cân
ta ̣i C . Go ̣i H và K lần lươ ̣t là trung điểm của AB và SB . Trong các khẳng đi ̣nh sau, khẳng đi ̣nh nào sai?
A. CH ⊥ SB .
B. AK ⊥ BC .
C. CH ⊥ SA.
D. CH ⊥ AK . 2 Câu 16: n + 1 Tính giới hạn lim ? 2 2n + n + 1 2 2 A. n + 1 n + 1 1 lim = 0 B. lim = 2 2n + n + 1 2 2n + n + 1 2 2 2 C. n + 1 n + 1 lim = +∞ D. lim = 1 2 2n + n + 1 2 2n + n + 1
Câu 17: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B , cạnh bên SA vuông góc với đáy, I
là trung điểm AC , H là hình chiếu của I lên SC . Khẳng định nào sau đây đúng?
A. (BIH ) ⊥ (SBC) .
B. (SAC) ⊥ (SAB) .
C. (SBC) ⊥ ( ABC) .
D. (SAC) ⊥ (SBC) . 3 2 Câu 18: mx mx
Cho hàm số f ( x) = −
+ (3 − m) x − 2 . Tìm m để f ( x) > 0 với mọi x 3 2 A. 12 0 < m < .
B. m < 0 . C. 12 m < D. 12 0 ≤ m < . 5 5 5
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 2/22 Mã đề 483
Câu 19: Tính đạo hàm của hàm số y = (x − x )2017 3 2 3 A. 2016 y = (x − x )2016 3 2 ' 2017 3 . B. y = ( 3 2 x − x ) ( 2 ' 2017 3
x − 3x ) . C. y = (x − x )2016 3 2 ( 2 ' 6051 3
x − 2x) . D. y = ( 3 2 x − x )( 2 ' 2017 3
3x − 6x ) . Câu 20: x + 2 Tính giới hạn lim ? 2
x→−2 2x + 5x + 2 A. x + 2 1 x + 2 lim = − . B. lim = 0 . 2
x→−2 2x + 5x + 2 3 2
x→−2 2x + 5x + 2 C. x + 2 1 x + 2 1 lim = − . D. lim = . 2
x→−2 2x + 5x + 2 2 2 x→ 2 − 2x + 5x + 2 2
Câu 21: Cho tứ diện ABCD . Gọi M , N là trung điểm của AD, BC . Khẳng định nào sau đây đúng ?
A. Các vectơ AB, AC, MN không đồng phẳng. B. Các vectơ DN, AC, MN đồng phẳng.
C. Các vectơ AB, DC, MN đồng phẳng.
D. Các vectơ AN,CM , MN đồng phẳng.
Câu 22: Trong các dãy số sau, dãy số nào có giới hạn khác 0 ? n   A. 2n −1 1 1 u = . B. u = . C. 1 u =   . D. u = . n n n n (n + ) 1 n  3  n 2 n +1
Câu 23: Cho cấp số cộng (u có công sai d , tìm điều kiện của d để (u là dãy số tăng n ) n ) A. d < 0. B. d > 1. C. d > 0. D. d ≥1. Câu 24: x +
Cho hàm số f ( x) 2 =
. Chọn khẳng định sai trong các khẳng định sau ? x 4 − x
A. Hàm số xác định trên (− ; ∞ 0) ∪ (0; 4) .
B. Hàm số liên tục tại x = 2.
C. Hàm số không liên tục tại x = 0 và x = 4. D. Vì f (− ) 1 1 = −
; f (2) = 2 nên f (− )
1 . f ( 2 ) < 0 , suy ra phương trình f ( x) = 0 có ít 5 nhất 1 nghiệm thuộc ( 1 − ; 2) .
Câu 25: Cho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A và D , có AD = CD = a ,
AB = 2a , SA ⊥ ( ABCD) , E là trung điểm của AB . Khẳng định nào sau đây đúng ?
A. CE ⊥ (SDC) .
B. CB ⊥ (SAB) . C. S
∆ CD vuông ở C .
D. CE ⊥ (SAB).
Câu 26: Xét các mệnh đề sau:
(1) Nếu hàm số f ( x) có đạo hàm tại điểm x = 0
x thì f ( x) liên tục tại điểm đó.
(2) Nếu hàm số f ( x) liên tục tại điểm x = 0
x thì f ( x) có đạo hàm tại điểm đó.
(3) Nếu f ( x) không liên tục tại x = 0
x thì chắc chắn f ( x) không có đạo hàm tại điểm đó.
(4) f ( x) có đạo hàm tại 0
x khi và chỉ khi f ( x) liên tục tại 0 x .
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng? A. 2 . B. 1. C. 4 . D. 3 .
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 3/22 Mã đề 483 Câu 27: 1
Cho hàm số f ( x) 3 2 =
x − 2x − 5x + 1. Giải phương trình f ′( x) = 0 . 3 A. {−1; } 5 . B. vô nghiệm. C. {1; − } 5 . D. {2 ± } 5 .
Câu 28: Gọi G là trọng tâm của tứ diện ABCD . Trong các khẳng định sau, khẳng định nào sai? A. 1 2 AG =
( AB + AC + AD).
B. AG = ( AB + AC + AD). 4 3 C. 1
GA + GB + GC + GD = 0 .
D. OG = (OA + OB + OC + OD). 4 2 x + x + x
Câu 29: Tính giới hạn lim ? x→−∞ x + 2 2 x + x + x 2 x + x + x A. lim = −∞ . B. lim = 2 − . x→−∞ x + 2 x→−∞ x + 2 2 x + x + x 2 x + x + x C. lim = 0 . D. lim = 2 . x→−∞ x + 2 x→−∞ x + 2 u  − u = 6
Câu 30: Cho cấp số cộng (un ) thỏa mãn 1 3 
, tìm số hạng tổng quát của cấp số cộng đó?  = − 5 u 10 A. u = 5 − 3 = = − = + n n . B. u 5 n n . C. 2 3 n u n . D. u 5 3 n n . 2 Câu 31: 2x
Cho hàm số f ( x) =
. Cho ̣n khẳng đi ̣nh đúng trong các khẳng đi ̣nh sau. x
A. Vı̀ lim f ( x) = lim f ( x) nên f ( x) liên tu ̣c ta ̣i x = 0 . x 0+ x 0− → →
B. Hàm số f ( x) xác đi ̣nh với mo ̣i x ≠ 0 .
C. lim f ( x) ≠ lim f ( x) . x 0− x 0+ → →
D. Hàm số f ( x) liên tu ̣c trên ℝ .
Câu 32: Tı̀m m để phương trı̀nh f ′( x) = 0 có nghiê ̣m. Biết f ( x) = mcos x + 2sin x − 3x +1 A. m > 0 . B. m ≥ 5 . C. m < 0 .
D. − 5 < m < 5 . 2 Câu 33: 2x − x + 5 Tı́nh giới ha ̣n lim − x ( → −3) x + 3 2 2 A. 2x − x + 5 2x − x + 5 lim = +∞ . B. lim = 2 . − − x ( → −3) x + 3 x ( → −3) x + 3 2 2 C. 2x − x + 5 2x − x + 5 lim = −∞ . D. lim = 2 − . − − x ( → −3) x + 3 x ( → −3) x + 3 x (1+ 2x)
Câu 34: Tı́nh đa ̣o hàm của hàm số y = 1− x 2 2 2 A. 1− 6x 4x +1 −6x + 2x +1 −2x + 4x +1 . B. . C. . D. . ( 2 2 1− x)2 (1− x)2 (1− x) (1− x)
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 4/22 Mã đề 483
Câu 35: Tı́nh đa ̣o hàm của hàm số 2
y = 3x − 4x + 5 A. 6x − 4 3x −1 1 3x − 2 . B. . C. . D. . 2 3x − 4x + 5 2 3x − 4x + 5 2 2 3x − 4x + 5 2 3x − 4x + 5
Câu 36: Một viên đạn được bắn lên trời từ một vị trí cách mặt đất 1000m theo phương thẳng đứng với
vận tốc ban đầu v = 294 m / s (bỏ qua sức cản của không khí). Hỏi khi viên đạn đạt độ cao lớn o
nhất và sẽ bắt đầu rơi thì viên đạn cách mặt đất bao nhiêu mét? A. 4307,5 . B. 5410 m . C. 4410 m . D. 4062,5m .
Câu 37: Chọn mệnh đề sai trong các mệnh đề sau? A. Hàm số 3 2
y = 2x −10x + 3x + 2017 liên tục tại mọi điểm x ∈ ℝ . B. 1 Hàm số y =
liên tục tại mọi điểm x ∈ ℝ . 2 x + x + 1 C. 1 Hàm số y =
liên tục tại mọi điểm x ≠ −1 . 3 x +1 D. x Hàm số y =
liên tục tại mọi điểm x ≠ 2 . 2 − x
Câu 38: Cho hình chóp S. ABC có đáy ABC là tam giác cân tại A , cạnh bên SA vuông góc với đáy,
M là trung điểm BC , J là trung điểm BM . Khẳng định nào sau đây đúng?
A. BC ⊥ (SAC ) .
B. BC ⊥ (SAJ ) .
C. BC ⊥ (SAM ) .
D. BC ⊥ (SAB) .
Câu 39: Cho tam giác ABC có ba góc ,
A B,C theo thứ tự lập thành một cấp số nhân với công bội
q = 2 . Tính số đo góc A ? A. π π π π . B. . C. 2 . D. 4 . 2 7 7 7
Câu 40: Cho tứ diện đều ABCD . Gọi ϕ là góc giữa hai mặt phẳng (BCD) và (ABC) . Khẳng định nào sau đây là đúng: A. 1 tan ϕ = . B. 0 ϕ = 60 . C. 1 cos ϕ = . D. 0 ϕ = 30 . 3 3
Câu 41: Tính tổng 10 số hạng đầu tiên của cấp số nhân (u , biết u = −3 và công bội q = 2 − . n ) 1 A. S = 1 − 023. B. S = 1025. 10 10 C. S = 1 − 025. D. S = 1023. 10 10
Câu 42: Viết phương trình tiếp tuyến của đồ thị hàm số f ( x) 3 2
= x − x + 2 , biết tiếp tuyến song song
với đường thẳng y = 5x + 5. A. 121 y = 5x − ; y = 5x + 5. B. 121 y = 5x + . 27 27
C. y = 5x − 5. D. 121 y = 5x − . 27
Câu 43: Trong các dãy số (u sau, hãy chọn dãy số tăng. n ) A. n u = − . n B. 1 u = . C. u = − n D. u = . n n ( ) 1 . n n n n
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 5/22 Mã đề 483
Câu 44: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song. 2 Câu 45: 2n − 3
Cho dãy số (u xác định bởi công thức số hạng tổng quát u =
với n ≥ 1, tìm số hạng n ) n n thứ ba của dãy số.
A. u = 5. B. u = 15. C. u = 4. D. u = 3. 3 3 3 3
Câu 46: Tính đạo hàm của hàm số: y = x tan 2x A. 2x x tan 2x + . B. tan 2x + . 2 cos x 2 cos 2x C. 2x 2
2x tan 2x + tan 2x + 2x . D. . 2 cos 2x
Câu 47: Cho hình chóp S.ABC có SA ⊥ (ABC) và tam giác ABC không vuông. Gọi H , K lần lượt là
trực tâm các tam giác ABC và tam giác SBC . Khẳng định nào sau đây đúng?
A. AH , SK , CB đồng phẳng.
B. AH , SK,CB đồng quy.
C. AH , SK , CB đôi một chéo nhau.
D. AH , SK , CB đôi một song song. Câu 48: a 3
Cho tứ diện ABCD có AB = CD = a , IJ =
. Gọi I , J lần lượt là trung điểm của BC 2
và AD . Tính số đo góc giữa hai đường thẳng AB và CD A. 0 90 . B. 0 45 . C. 0 60 . D. 0 30 .
Câu 49: Cho hình chóp SABCD có ABCD là hình thoi tâm O và SA = SC, SB = SD . Trong các khẳng
định sau khẳng định nào sai?
A. AC ⊥ SA.
B. SA ⊥ BD .
C. AC ⊥ BD .
D. SD ⊥ AC . Câu 50: 1
Cho cấp số nhân (u ) với u = −
, u = −32 .Tìm công bội q của cấp số nhân trên? n 1 2 7 A. q = ±1. B. q = ±4 . C. 1 q = ± . D. q = ±2 . 2 ---- Hết ----
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 6/22 Mã đề 483 BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C D B A C D A A A C C C A D B B A D C A C A C D D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A A B B A B B C D D B D C C C D D D B A C B C A D
HƯỚNG DẪN GIẢI
Câu 1: Viết phương trình tiếp tuyến của đồ thị hàm số 3 2
f (x) = x − 2x + 3x +1 tại điểm có hoành độ x = 2 . 0
A. y = −x − 7
B. y = 7x −14
C. y = 7x − 7
D. y = −x + 9 Hướng dẫn giải Chọn C.
Với x = 2 ⇒ y = 7 0 0 Ta có 2 f (
′ x) = 3x − 4x + 3 ⇒ f ( ′ 2) = 7
Vậy PTTT cần tìm là y = f (
′ 2)( x − 2) + 7 = 7x − 7 Câu 2: 1 + x − 1 Tính giới hạn lim ? x→0 x A. 1 + x − 1 1 1 + x − 1 1 + x − 1 1 + x − 1 1 lim = − . B. lim = +∞ . C. lim = 0 . D. lim = . x→0 x 2 x→0 x x→0 x x→0 x 2 Hướng dẫn giải: Chọn D. x 1 ( 1+ x −1)( 1+x +1 1 + − ) x 1 1 lim = lim = lim = lim = x→0 x x →0 x ( 1+ x + 1) x→0 x ( 1+ x +1) x→0 + + 2 1 x 1
Câu 3: Cho hàm số: f ( x) = 3 + x . Tính f ( ) 1 + 4 f ′( ) 1 . A. 1. B. 3 . C. 1 . D. 0 . 4 Hướng dẫn giải Chọn B. Ta có f ( x) =
+ x ⇒ f ′( x) 1 3 = 2 3+ x
Nên f ( ) + f ′( ) 4 1 4 1 = 3 +1 + = 3 2 3 +1 Câu 4: Cho hàm số: 3 2
f (x) = x − 3x + 4. Tính f ( ′ 1). A. 3 − . B. 0 . C. 9 . D. 3 . Hướng dẫn giải Chọn A. Ta có 2 f (
′ x) = 3x − 6x ⇒ f ( ′ 1) = 3 − 6 = −3. Câu 5: n π
Cho dãy số (u với u = −
, chọn khẳng định đúng trong các khẳng định sau? n ( ) 1 sin n ) n
A. Dãy số (u là dãy số tăng. n )
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 7/22 Mã đề 483
B. Dãy số (u bị chặn dưới nhưng không bị chặn trên. n )
C. Dãy số (u bị chặn. n )
D. Dãy số (u bị chặn trên nhưng không bị chặn dưới. n ) Hướng dẫn giải Chọn C. n π π Ta có: u = − =
≤ . Vì vậy dãy số (u là dãy bị chặn. n ) n ( ) 1 sin sin 1 n n
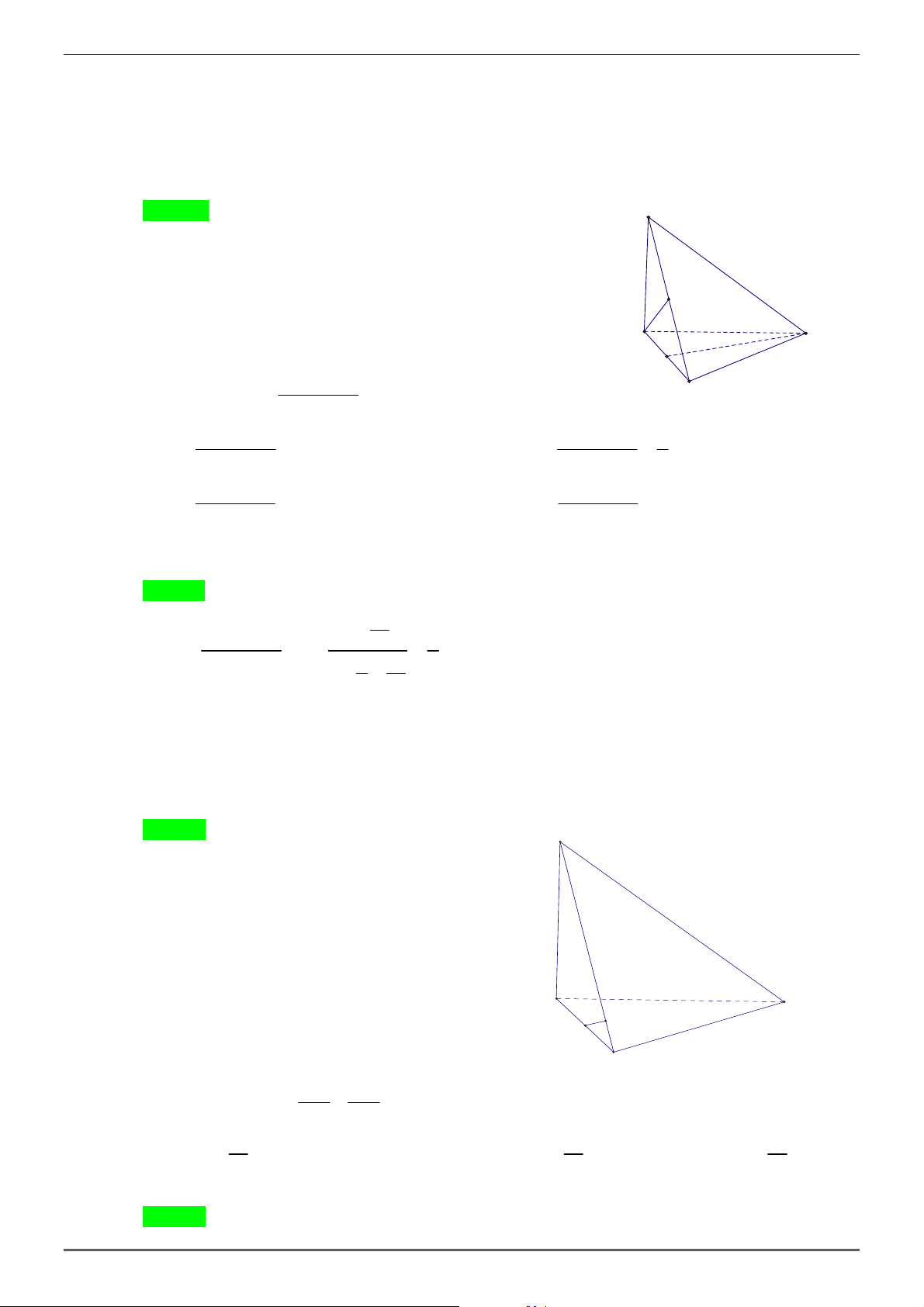
Câu 6: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , AB = a , SA = SB = SC . Góc
giữa đường thẳng SA và mặt phẳng ( ABC ) bằng 0
45 . Tính theo a khoảng cách từ điểm S
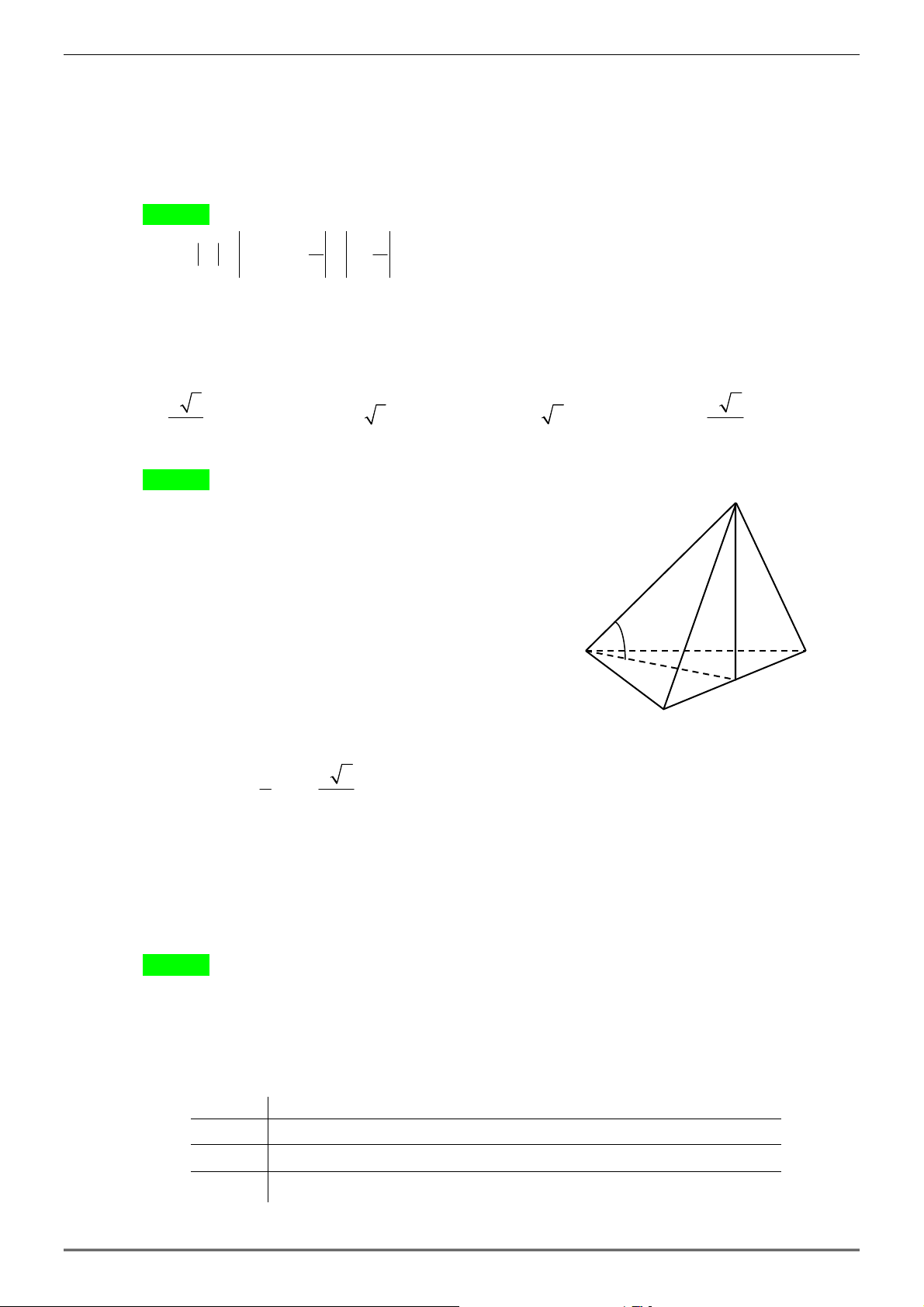
đến mặt phẳng ( ABC ) . A. a 3 a . B. a 3 . C. a 2 . D. 2 . 3 2 Hướng dẫn giải Chọn D. S
Gọi H là hình chiếu của S trên ( ABC ) .
⇒ SH ⊥ ( ABC) ⇒ SH = d (S;( ABC)) . Ta có S ∆ HA = S ∆ HB = ∆SHC
⇒ HA = HB = HC ⇒ H là tâm đường tròn ngoại tiếp tam giác ABC . 0 45 Mặt khác A
∆ BC vuông tại A nên H là trung điểm A C của BC . a H
Do SH ⊥ ( ABC ) B
⇒ (SA ( ABC)) = (SA AH ) 0 ; ; = SAH = 45 . 1 a 2
⇒ SH = AH = BC = . 2 2
Câu 7: Cho hàm số f ( x) 4 2
= x − 2x +1. Tìm x để f ′( x) > 0 A. x ∈( 1 − ; 0) ∪ (1; +∞) . B. x ∈( 1 − ; ) 1 .
C. x ∈(−∞;− ) 1 ∪ (0; ) 1 . D. x ∈ ℝ . Hướng dẫn giải. Chọn A. Ta có f ′( x) 3
= x − x = x ( 2 4 4 4 x − ) 1 .
f ′( x) > ⇔ x ( 2 0 4 x − ) 1 > 0 . Lập bảng xét dấu: x −∞ 1 − 0 1 +∞ 4x − | − 0 + | + 2 x −1 + 0 − | − 0 + f ′( x) − 0 + 0 − 0 +
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 8/22 Mã đề 483
Từ bảng xét dấu suy ra: f ′( x) > 0 ⇔ x ∈ ( 1 − ; 0) ∪ (1;+∞) .
Câu 8: Tìm tất cả các giá trị của x để ba số 2
1− x, x ,1+ x theo thứ tự lập thành cấp số cộng? A. x = 1 ± . B. x = 2 ± . C. x = 1. D. x = 1 − . Hướng dẫn giải. Chọn A. Cách 1: Ta có ba số 2
1− x, x ,1+ x theo thứ tự lập thành cấp số cộng 2
⇔ 1− x +1+ x = 2x ⇔ x = 1 ± .
Cách 2: Thử giá trị trong đáp án:
Với x = 1 thì ba số là 0;1; 2 lập thành CSC nên thoả mãn. Với x = 1
− thì ba số là 2;1; 0 lập thành CSC nên thoả mãn. Vậy chọn A.
Câu 9: Trong các dãy số sau, dãy số nào không là cấp số cộng? A. 1 1 1 1 1 ; ; ; ; . B. 1 3 5 7 9 ; ; ; ; . C. 8 − ; −6; 4 − ; 2 − ;0 . D. 2; 2; 2; 2; 2 . 2 4 6 8 10 2 2 2 2 2 Hướng dẫn giải. Chọn A.
Kiểm tra từng đáp án tính chất a
− a = d với n
d không đổi với n ∀ . 1 + n 1 1 1 1 Với đáp án A: − ≠ −
nên dãy số ở đáp án A không là CSC 4 2 6 4
Các đáp án khác đều thoả mãn.
Câu 10: Tính đạo hàm của hàm số y = 2sin 3x + cos 2x .
A. y′ = 2cos3x − sin 2x .
B. y′ = 2cos3x + sin 2x .
C. y′ = 6cos3x − 2sin 2x .
D. y′ = −6cos3x + 2sin 2x . Hướng dẫn giải. Chọn C Ta có y
2 (sin 3x)′ (cos 2x)′ 2 cos 3 .
x (3x)′ sin 2 . x (2x)′ ′ = + = −
= 6 cos 3x − 2 sin 2x .
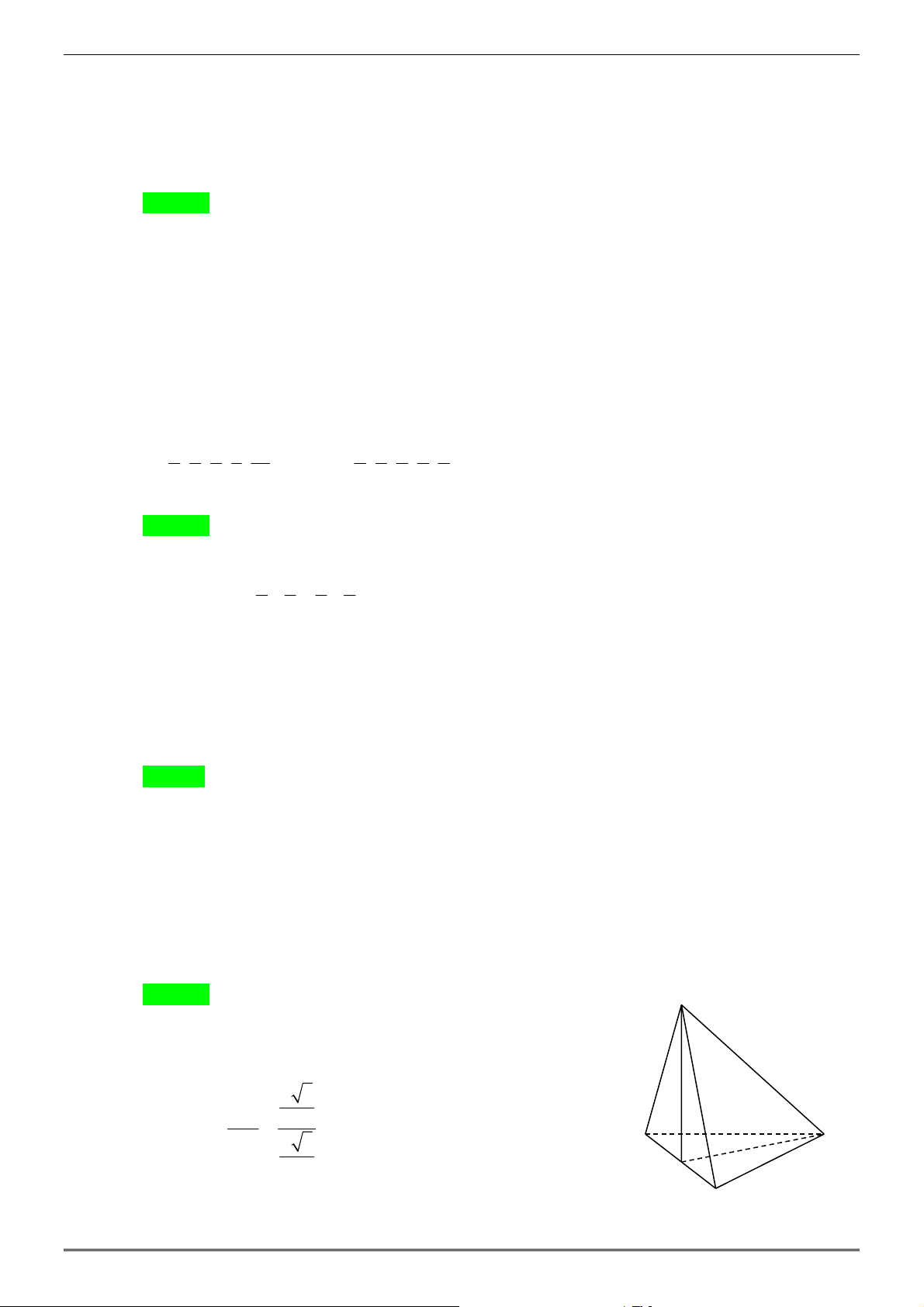
Câu 11: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông góc của S lên
( ABC ) trùng với trung điểm H của cạnh BC . Biết tam giác SBC là tam giác đều. Tính số đo
của góc giữa SA và ( ABC ) A. 30° . B. 45° . C. 60° . D. 90° . Hướng dẫn giải Chọn C. S
SA có hình chiếu lên ( ABC ) là HA .
Vậy góc giữa SA và ( ABC ) là SAH . a 3 AH an 2 t SAH = = = 1. SH B A a 3 2 H
Vậy góc giữa SA và ( ABC ) có số đo là 45° . C
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 9/22 Mã đề 483
Câu 12: Tính giới hạn ( 2 lim
n − n − n) ? A. ( 2 lim
n − n − n) = +∞ . B. ( 2 lim
n − n − n) = 1 − . C. lim( 1 2
n − n − n) = − . D. ( 2 lim
n − n − n) = 0. 2 Hướng dẫn giải. Chọn C −n − lim ( 1 1 2
n − n − n) = lim = lim = −
( 2n −n +n) 1 2 1− +1 n
Câu 13: Cho hı̀nh lăng tru ̣ ABC. ′
A B′C′ có tất cả các ca ̣nh đều bằng a . Góc ta ̣o bởi ca ̣nh bên và mă ̣t
phẳng đáy bằng 30° . Hı̀nh chiếu H của ′
A lên mă ̣t phẳng ( ABC ) thuô ̣c đường thẳng BC .
Tı́nh khoảng cách từ B đến mă ̣t phẳng ( ACC′ ′ A ) A. a 21 a a a . B. 3 . C. 3 . D. 21 . 7 4 2 14 Hướng dẫn giải. Chọn A A' a 3 C' Ta có ′
A AH = 30° do đó AH = . a cos 30° = và 2 a 3 1 a B' ′ A H = . =
. Go ̣i K là hı̀nh chiếu của H lên AC và 2 3 2 I
I là hı̀nh chiếu của H lên ′ A K . K A
Do tam giác ABC đều ca ̣nh bằng a nên H thuô ̣c đoa ̣n BC C
và H là trung điểm BC . H B d ( , B ( ACC′ ′
A )) = 2d ( H ,( ACC′ ′ A )) = 2HI . 2 a a 3 a 3 . 1 a 3 a 3 HA .′HK a 21 HK = = nên 2 4 4 2HI = 2 = 2 = = . 2 2 4 2 2 2 2 2 H ′ A + HK a 3a 7a 7 + 4 16 16
Câu 14: Trong các mê ̣nh đề sau, mê ̣nh đề nào đúng?
A. Hai đường thẳng cùng vuông góc với mô ̣t đường thẳng thı̀ song song với nhau.
B. Hai đường thẳng cùng vuông góc với mô ̣t đường thẳng thı̀ vuông góc với nhau.
C. Mô ̣t đường thẳng vuông góc với mô ̣t trong hai đường thẳng vuông góc thı̀ song song với
đường thẳng còn la ̣i.
D. Mô ̣t đường thẳng vuông góc với mô ̣t trong hai đường thẳng song song thı̀ vuông góc với đường thẳng kia. Hướng dẫn giải. Chọn D.
Tı́nh chất cơ bản trong SGK hı̀nh ho ̣c 11.
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 10/22 Mã đề 483
Câu 15: Cho hı̀nh chóp SABC có SA vuông góc với mă ̣t phẳng ( ABC ) và đáy ABC là tam giác cân
ta ̣i C . Go ̣i H và K lần lươ ̣t là trung điểm của AB và SB . Trong các khẳng đi ̣nh sau, khẳng đi ̣nh nào sai?
A. CH ⊥ SB .
B. AK ⊥ BC .
C. CH ⊥ SA.
D. CH ⊥ AK . Hướng dẫn giải. Chọn B. S
Ta có CH ⊥ (SAB) nên CH ⊥ SB suy ra A đúng và
CH ⊥ AK nên D đúng
Do SA ⊥ ( ABC ) nên C đúng. Vâ ̣y cho ̣n B. K A C H 2 Câu 16: n + 1 Tính giới hạn lim ? B 2 2n + n + 1 2 2 A. n + 1 n + 1 1 lim = 0 B. lim = 2 2n + n + 1 2 2n + n + 1 2 2 2 C. n + 1 n + 1 lim = +∞ D. lim = 1 2 2n + n + 1 2 2n + n + 1 Hướng dẫn giải Chọn B. 1 2 1 + 2 n + 1 1 Vì: lim = lim n = 2 2n + n + 1 1 1 2 2 + + 2 n n
Câu 17: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B , cạnh bên SA vuông góc với đáy, I
là trung điểm AC , H là hình chiếu của I lên SC . Khẳng định nào sau đây đúng?
A. (BIH ) ⊥ (SBC) .
B. (SAC) ⊥ (SAB) . C. (SBC) ⊥ ( ABC) . D. (SAC) ⊥ (SBC) . Hướng dẫn giải Chọn A. S BI ⊥ SA Vì 
⇒ BI ⊥ (SAC) ⇒ (BIH ) ⊥ (SAC) BI ⊥ AC A B H I C 3 2 Câu 18: mx mx
Cho hàm số f ( x) = −
+ (3 − m) x − 2 . Tìm m để f ( x) > 0 với mọi x 3 2 A. 12 0 < m < .
B. m < 0 . C. 12 m < D. 12 0 ≤ m < . 5 5 5 Hướng dẫn giải Chọn D.
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 11/22 Mã đề 483 f ( x) 2 '
= mx − mx + (3 − m) , để f ( x) > 0 với mọi x thì
TH1: m = 0 ⇒ 3 > 0 đúng m > 0 m > 0 12 TH2:  ⇔  ⇔ 0 < m < 2
∆ = m − 4m(3 − m) 2 < 0
5m −12m < 0 5 Đ 12
áp số: 0 ≤ m < 5
Câu 19: Tính đạo hàm của hàm số y = (x − x )2017 3 2 3 A. 2016 y = (x − x )2016 3 2 ' 2017 3 . B. y = ( 3 2 x − x ) ( 2 ' 2017 3
x − 3x ) . C. y = (x − x )2016 3 2 ( 2 ' 6051 3
x − 2x) . D. y = ( 3 2 x − x )( 2 ' 2017 3
3x − 6x ) . Hướng dẫn giải Chọn C. y =
(x − x )2016 ( x − x) = (x − x )2016 3 2 2 3 2 ( 2 ' 2017 3 3 6 6051 3 x − 2x ) Câu 20: x + 2 Tính giới hạn lim ? 2
x→−2 2x + 5x + 2 A. x + 2 1 x + 2 lim = − . B. lim = 0 . 2 2
x→−2 2x + 5x + 2 3
x→−2 2x + 5x + 2 C. x + 2 1 x + 2 1 lim = − . D. lim = . 2 2
x→−2 2x + 5x + 2 2 x→ 2 − 2x + 5x + 2 2 Hướng dẫn giải Chọn A x + 2 x + 2 1 1 − lim = lim = lim = 2 x→−2 x→−2 2x + 5x + 2
( x + 2)(2x + ) x→ 2 1 − 2x + 1 3
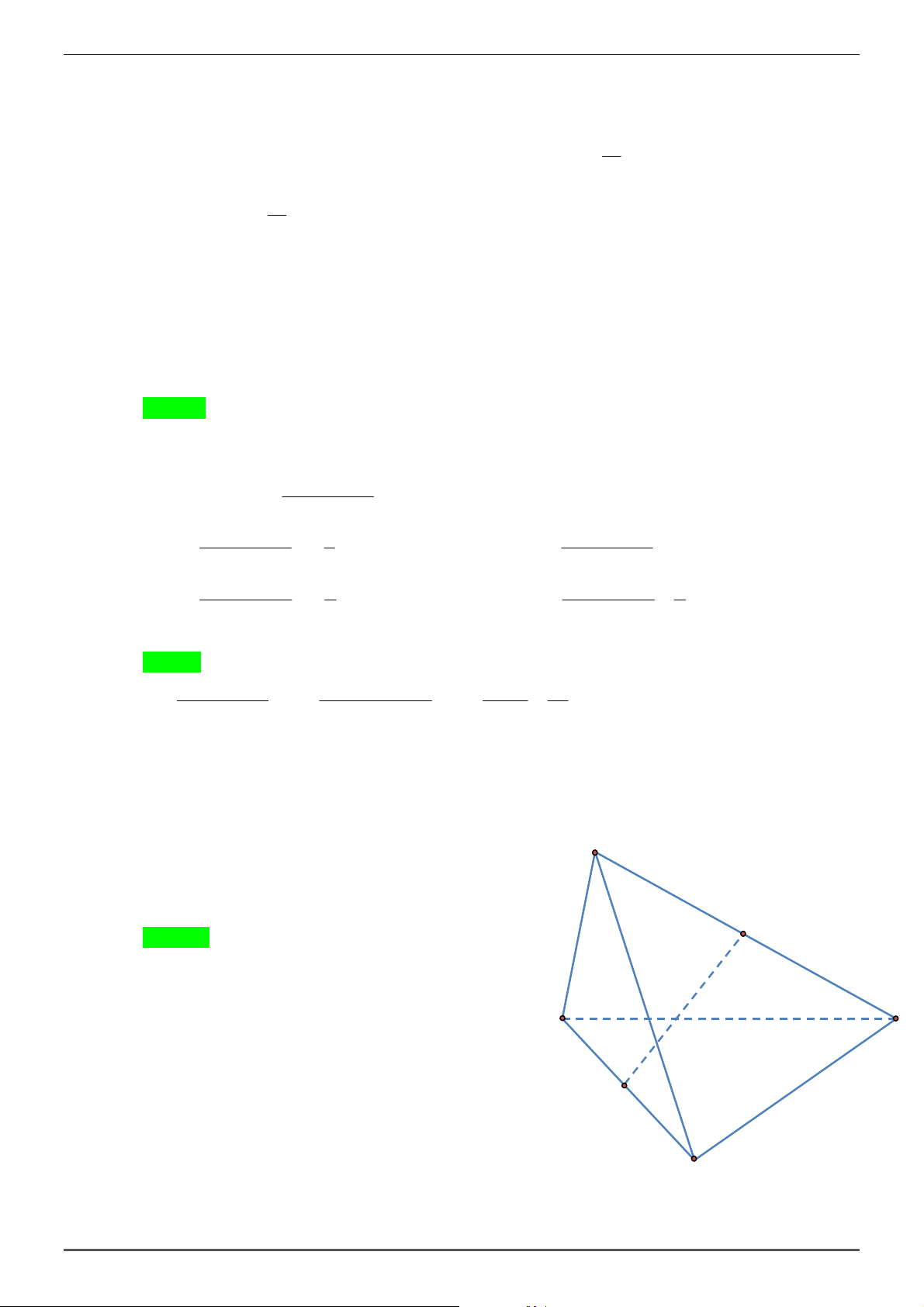
Câu 21: Cho tứ diện ABCD . Gọi M , N là trung điểm của AD, BC . Khẳng định nào sau đây đúng ?
A. Các vectơ AB, AC, MN không đồng phẳng.
B. Các vectơ DN, AC, MN đồng phẳng. A
C. Các vectơ AB, DC, MN đồng phẳng.
D. Các vectơ AN,CM , MN đồng phẳng. Hướng dẫn giải M Chọn C.
AB + DC = AM + MN + NB + DM + MN + NC
= ( AM + DM ) + 2MN + ( NB + NC) B D
Vì M , N là trung điểm của AD, BC
AM + DM = 0 Nên : 
NB + NC = 0 N
Vậy AB + DC = 2MN .
Nên các vectơ AB, DC, MN đồng phẳng C
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 12/22 Mã đề 483
Câu 22: Trong các dãy số sau, dãy số nào có giới hạn khác 0 ? n   A. 2n −1 1 1 u = . B. u = . C. 1 u =   . D. u = . n n n n (n + ) 1 n  3  n 2 n +1 Hướng dẫn giải Chọn A. 1 2 − 2n −1 2 n lim = lim = = 2 ≠ 0 n 1 1
Câu 23: Cho cấp số cộng (u có công sai d , tìm điều kiện của d để (u là dãy số tăng n ) n ) A. d < 0. B. d > 1. C. d > 0. D. d ≥1. Hướng dẫn giải Chọn C.
(u là dãy số tăng khi và chỉ khi * u − u > 0, n ∀ ∈ N n ) n 1 + n
⇔ u + nd − u + n −1 d > 0 1 ( 1 ( ) ) ⇔ d > 0 Câu 24: x +
Cho hàm số f ( x) 2 =
. Chọn khẳng định sai trong các khẳng định sau ? x 4 − x
A. Hàm số xác định trên (− ; ∞ 0) ∪ (0; 4) .
B. Hàm số liên tục tại x = 2.
C. Hàm số không liên tục tại x = 0 và x = 4. D. Vì f (− ) 1 1 = −
; f (2) = 2 nên f (− )
1 . f ( 2 ) < 0 , suy ra phương trình f ( x) = 0 có ít 5 nhất 1 nghiệm thuộc ( 1 − ; 2) . Hướng dẫn giải Chọn D.
Tập xác định : D = (− ; ∞ 0) ∪ (0;4)
Hay hàm số liên tục trên (− ;
∞ 0) và (0; 4) . Từ đó suy ra hàm số không liên tục trên [ 1 − ; 2]. Vậy D sai.
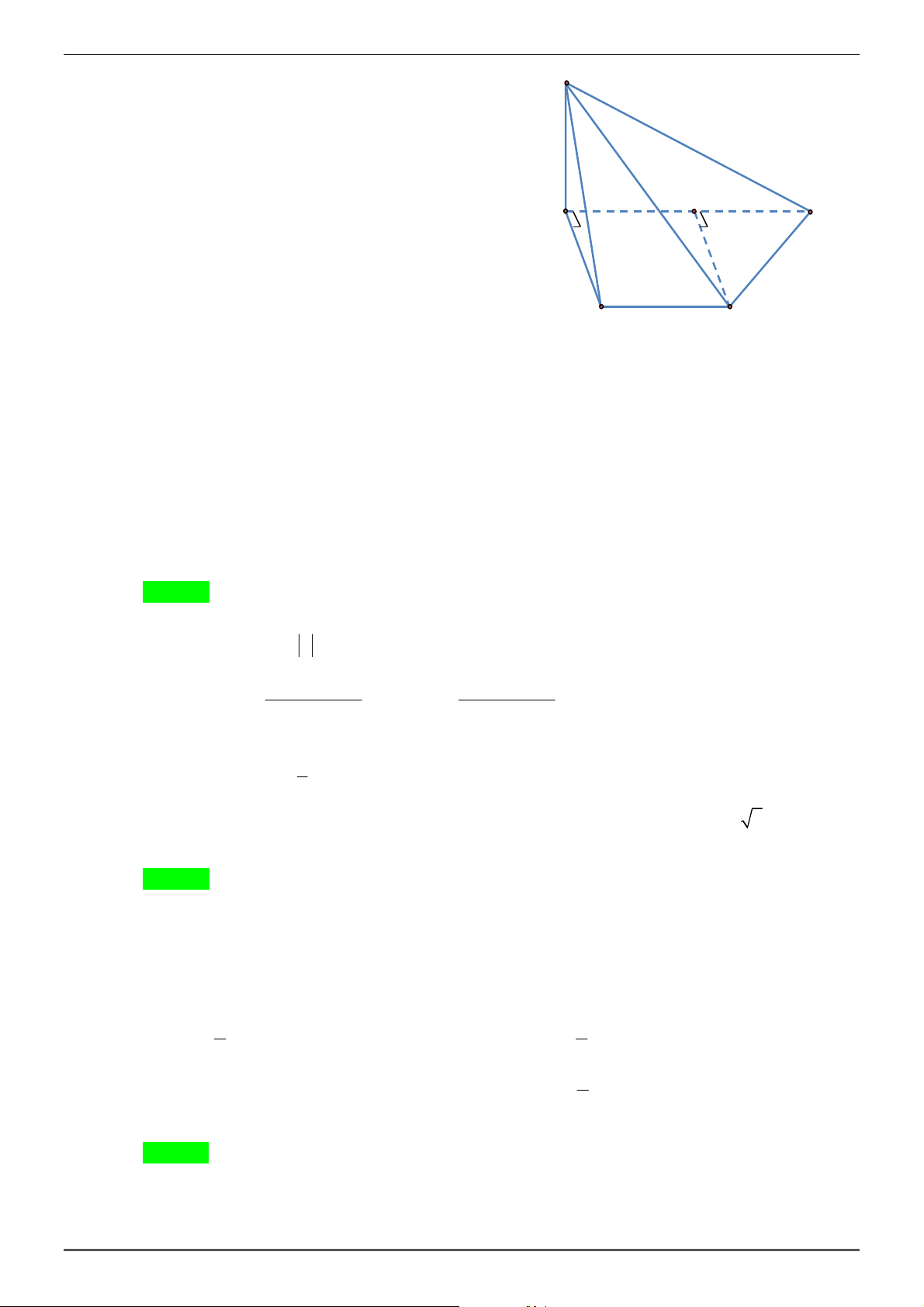
Câu 25: Cho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A và D , có AD = CD = a ,
AB = 2a , SA ⊥ ( ABCD) , E là trung điểm của AB . Khẳng định nào sau đây đúng ?
A. CE ⊥ (SDC) .
B. CB ⊥ (SAB) C. SC ∆ D vuông ở C
D. CE ⊥ (SAB). Hướng dẫn giải Chọn D.
Xét tứ giác AECD có :
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 13/22 Mã đề 483  S AE / /CD
AE = CD = AD = a   A = 90°
Nên AECD là hình vuông. CE ⊥ AB E Có : 
⇒ CE ⊥ (SAB) . A B CE ⊥ SA Vậy D đúng. D C
Câu 26: Xét các mệnh đề sau:
(1) Nếu hàm số f ( x) có đạo hàm tại điểm x = 0
x thì f ( x) liên tục tại điểm đó.
(2) Nếu hàm số f ( x) liên tục tại điểm x = 0
x thì f ( x) có đạo hàm tại điểm đó.
(3) Nếu f ( x) không liên tục tại x = 0
x thì chắc chắn f ( x) không có đạo hàm tại điểm đó.
(4) f ( x) có đạo hàm tại 0
x khi và chỉ khi f ( x) liên tục tại 0 x .
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng? A. 2 . B. 1. C. 4 . D. 3 . Hướng dẫn giải Chọn A.
Theo định lý 1 thì (1) và (3) đúng.
Xét hàm số: f ( x) = x ta có: lim f ( x) = 0 và lim f ( x) = 0 nên hàm số liên tục tại x = 0 . x 0+ → x 0− →
f ( x) − f (0)
f ( x) − f (0) Mặt khác: lim = 1 và lim
= −1 nên hàm số không có đạo hàm tại x 0+ → x − 0 x 0− → x − 0
x = 0 . Vậy (2) và (4) sai. Câu 27: 1
Cho hàm số f ( x) 3 2 =
x − 2x − 5x + 1. Giải phương trình f ′( x) = 0 . 3 A. {−1; } 5 . B. vô nghiệm. C. {1; − } 5 . D. {2 ± } 5 . Hướng dẫn giải Chọn A.
Ta có: f ′( x) 2
= x − 4x − 5 . x = −
Do đó f ′( x) = 0 2 1
⇔ x − 4x − 5 = 0 ⇔ x = 5
Câu 28: Gọi G là trọng tâm của tứ diện ABCD . Trong các khẳng định sau, khẳng định nào sai? A. 1 2 AG =
( AB + AC + AD).
B. AG = ( AB + AC + AD). 4 3 C. 1
GA + GB + GC + GD = 0 .
D. OG = (OA + OB + OC + OD). 4 Hướng dẫn giải Chọn B.
Ta có: GA + GB + GC + GD = 0 ⇔ AG = GB + GC + GD
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 14/22 Mã đề 483
⇔ AG = ( AB − AG) + ( AC − AG) + ( AD − AG) 1 ⇔ AG =
(AB + AC + AD). 4 2 x + x + x
Câu 29: Tính giới hạn lim ? x→−∞ x + 2 2 x + x + x 2 x + x + x A. lim = −∞ . B. lim = 2 − . x→−∞ x + 2 x→−∞ x + 2 2 x + x + x 2 x + x + x C. lim = 0 . D. lim = 2 . x→−∞ x + 2 x→−∞ x + 2 Hướng dẫn giải Chọn B.  1  1 1 −x 1+ 1+  2 x + x 1+ 1+ 1+ x + x + xx xx lim = lim = lim = − lim = −2 . x→−∞ x + 2 x→−∞  2  x→−∞  2  x→−∞ 2 x 1+  x 1+  1+  x   x x u  − u = 6
Câu 30: Cho cấp số cộng (un ) thỏa mãn 1 3 
, tìm số hạng tổng quát của cấp số cộng đó?  5 u = 1 − 0 A. u = 5 − 3 = = − = + n n . B. u 5 n n . C. 2 3 n u n . D. u 5 3 n n . Hướng dẫn giải Chọn A. Gọi 1
u là số hạng đầu và d là công sai của cấp số cộng. theo đề ta có hệ phương trình:   1 u − ( 1 u + 2d ) = 6 d = −3  ⇔  u  + 4d = −10 u  = 2 1 1
Số hạng tổng quát: u = + − = + − − = − 1 u (n ) 1 d 2 (n ) 1 ( 3) 5 3 n n . 2 Câu 31: 2x
Cho hàm số f ( x) =
. Cho ̣n khẳng đi ̣nh đúng trong các khẳng đi ̣nh sau. x
A. Vı̀ lim f ( x) = lim f ( x) nên f ( x) liên tu ̣c ta ̣i x = 0 . x 0+ x 0− → →
B. Hàm số f ( x) xác đi ̣nh với mo ̣i x ≠ 0 .
C. lim f ( x) ≠ lim f ( x) . x 0− x 0+ → →
D. Hàm số f ( x) liên tu ̣c trên ℝ .
Hướng dẫn giải Cho ̣n B. 2 2x lim
= lim 2x = 0 ; lim f ( x) = lim 2x = 0 x 0+ x 0 x + → → x 0− x 0− → →
lim f ( x) = lim f ( x) nên f ( x) liên tu ̣c ta ̣i x = 0 . x 0+ x 0− → → 2 2x
Hàm số f ( x) =
không xác định tại x = 0 . x 2 2x
Với mọi x ≠ 0 hàm số f ( x) = = 2x . x
Câu 32: Tı̀m m để phương trı̀nh f ′( x) = 0 có nghiê ̣m. Biết f ( x) = mcos x + 2sin x − 3x +1
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 15/22 Mã đề 483 A. m > 0 . B. m ≥ 5 . C. m < 0 .
D. − 5 < m < 5 .
Hướng dẫn giải Chọn B.
f ′( x) = −m sin x + 2cos x − 3
f ′( x) = 0 ⇔ −m sin x + 2 cos x − 3 = 0 ⇔ −msin x + 2 cos x = 3 (∗)
Phương trình (∗) có nghiệm khi (−m)2 2 2 2
+ 2 ≥ 3 ⇔ m ≥ 5 ⇔ m ≥ 5 . 2 Câu 33: 2x − x + 5 Tı́nh giới ha ̣n lim − x ( → −3) x + 3 2 2 A. 2x − x + 5 2x − x + 5 lim = +∞ . B. lim = 2 . − − x ( → −3) x + 3 x ( → −3) x + 3 2 2 C. 2x − x + 5 2x − x + 5 lim = −∞ . D. lim = 2 − . − − x ( → −3) x + 3 x ( → −3) x + 3
Hướng dẫn giải Chọn C lim − + = > − ( 2 2x x 5) 26 0 x ( → −3) −
lim ( x + 3) = 0 và x → (−3) thì x + 3 < 0 . − x→(−3) 2 2x − x + 5 Suy ra lim = −∞ . − x ( → −3) x + 3 x (1+ 2x)
Câu 34: Tı́nh đa ̣o hàm của hàm số y = 1− x 2 2 2 A. 1− 6x 4x +1 −6x + 2x +1 −2x + 4x +1 . B. . C. . D. . ( 2 2 1− x)2 (1− x)2 (1− x) (1− x)
Hướng dẫn giải Chọn D. x ( + x) 2 1 2 x + 2x y = = 1− x 1− x ( 2 ′ x 2x ) (1 x) ( 2 x 2x )(1 x)′ + − − + −
(1+ 4x)(1− x) − ( 2 x + 2x )(− ) 2 1 −2x + 4x + 1 y′ = = = (1− x)2 (1− x)2 (1− x)2 y . 5410 (t=30)
Câu 35: Tı́nh đa ̣o hàm của hàm số 2
y = 3x − 4x + 5 A. 6x − 4 3x −1 1 3x − 2 . B. . C. . D. . 2 3x − 4x + 5 2 3x − 4x + 5 2 2 3x − 4x + 5 2 3x − 4x + 5
Hướng dẫn giải Chọn D. ( 2 ′ 3x − 4x + 5) 6x − 4 3x − 2 y′ = = = . 2 2 2 2 3x − 4x + 5 2 3x − 4x + 5 3x − 4x + 5 A 1000 (t=0)
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 16/22 Mã đề 483 O
Câu 36: Một viên đạn được bắn lên trời từ một vị trí cách mặt đất 1000m theo phương thẳng đứng với
vận tốc ban đầu v = 294 m / s (bỏ qua sức cản của không khí). Hỏi khi viên đạn đạt độ cao lớn o
nhất và sẽ bắt đầu rơi thì viên đạn cách mặt đất bao nhiêu mét? A. 4307,5 . B. 5410 m . C. 4410 m . D. 4062,5m .
Hướng dẫn giải Chọn B.
Chọn trục Oy theo phương thẳng đứng, chiều dương hướng từ mặt đất lên trời, gốc O ở mặt
đất và cách A là vị trí viên đạn được bắn lên, gốc thời gian (tức lúc t = 0 ) được tính từ vị trí A
như hình bên; khi đó chuyển động của viên đạn là chuyển động biến đổi đều với vận tốc ban
đầu v = 294 m / s và với gia tốc. (Gia tốc nhận giá trị âm vì véc tơ gia tốc ngược chiều dương o
của trục Oy . Phương trình chuyển động của viên đạn là: 2
y = 1000 + 294t − 4,9t
Ta có v (t ) = y′ = 294 − 9,8t
Viên đạn đạt độ cao lớn nhất và sẽ bắt đầu rơi v (t ) = 0 ⇔ 294 − 9,8t = 0 ⇔ t = 30( s)
Khi đó viên đạn cách mặt đất là y ( ) 2
30 = 1000 + 294.30 − 4,9.30 = 5410(m)
Câu 37: Chọn mệnh đề sai trong các mệnh đề sau? A. Hàm số 3 2
y = 2x −10x + 3x + 2017 liên tục tại mọi điểm x ∈ ℝ . B. 1 Hàm số y =
liên tục tại mọi điểm x ∈ ℝ . 2 x + x + 1 C. 1 Hàm số y =
liên tục tại mọi điểm x ≠ −1 . 3 x +1 D. x Hàm số y =
liên tục tại mọi điểm x ≠ 2 . 2 − x
Hướng dẫn giải Chọn D
Mệnh đề A đúng vì hàm số 3 2
y = 2x −10x + 3x + 2017 là hàm đa thức có tập xác định ℝ nên
hàm số liên tục tại mọi điểm x ∈ ℝ . 1
Mệnh đề B đúng vì hàm số y =
là hàm phân thức hữu tỉ, có tập xác định ℝ nên hàm 2 x + x + 1
số liên tục tại mọi điểm x ∈ ℝ . 1
Mệnh đề C đúng vì hàm số y =
là hàm phân thức hữu tỉ, có tập xác định ℝ \ { } 1 − nên 3 x +1
hàm số liên tục tại mọi điểm x ≠ −1 . x
Mệnh đề D sai vì hàm số y =
có tập xác định D = (− ;
∞ 2) nên hàm số bị gián đoạn tại 2 − x
các điểm x ∈[2;+ ∞)
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 17/22 Mã đề 483
Câu 38: Cho hình chóp S. ABC có đáy ABC là tam giác cân tại A , cạnh bên SA vuông góc với đáy,
M là trung điểm BC , J là trung điểm BM . Khẳng định nào sau đây đúng?
A. BC ⊥ (SAC ) .
B. BC ⊥ (SAJ ) .
C. BC ⊥ (SAM ) .
D. BC ⊥ (SAB) .
Hướng dẫn giải S Chọn C.
Tam giác ABC là tam giác cân tại A , AM là đường trung tuyến
đồng thời là đường cao nên AM ⊥ BC
Lại có SA ⊥ ( ABC ) , BC ⊂ ( ABC ) ⇒ SA ⊥ BC A C
Từ đó suy ra BC ⊥ (SAM ) . M B
Câu 39: Cho tam giác ABC có ba góc ,
A B,C theo thứ tự lập thành một cấp
số nhân với công bội q = 2 . Tính số đo góc A? A. π π π π . B. . C. 2 . D. 4 . 2 7 7 7
Hướng dẫn giải Chọn C. Theo giả thiết ta có ,
A B,C lập thành cấp số nhân với q = 2 nên B = 2 ; A C = 4 A π
Mà ABC là một tam giác nên A + 2 A + 4 A = π ⇔ A = 7
Câu 40: Cho tứ diện đều ABCD . Gọi ϕ là góc giữa hai mặt phẳng (BCD) và (ABC) . Khẳng định nào sau đây là đúng: A. 1 tan ϕ = . B. 0 ϕ = 60 . C. 1 cos ϕ = . D. 0 ϕ = 30 . 3 3
Hướng dẫn giải Chọn C. A
Giả sử tứ diện đều có tất cả các cạnh bằng x
Gọi M là trung điểm BC AM ⊥ BC
Do tam giác ABC, DBC đều nên  DM ⊥ BC B
Do đó: ϕ = ( AM ; DM ) D x 3
Xét tam giác AMD có: AM = DM = M 2 Nên C
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 18/22 Mã đề 483 2 2 3x 3x 1 2 2 2 2 2 + − x x
AM + MD − AD 1 4 4 2 cos AMD = = = = > 0 Nên 2 2.AM .MD x 3 x 3 3x 3 2. . 2 2 2
cos AMD = cos( AM ; MD) = cosϕ 1 Vậy cosϕ = . 3
Câu 41: Tính tổng 10 số hạng đầu tiên của cấp số nhân (u , biết u = −3 và công bội q = 2 − . n ) 1 A. S = 1 − 023. B. S = 1025. C. S = 1 − 025. D. S = 1023. 10 10 10 10
Hướng dẫn giải Cho ̣n D. u ( 10 1− q 1 ) Ta có: S = = 1023. 10 1− q
Câu 42: Viết phương trình tiếp tuyến của đồ thị hàm số f ( x) 3 2
= x − x + 2 , biết tiếp tuyến song song
với đường thẳng y = 5x + 5. A. 121 y = 5x − ; y = 5x + 5. B. 121 y = 5x + . 27 27
C. y = 5x − 5. D. 121 y = 5x − . 27
Hướng dẫn giải Cho ̣n D. + f ′( x) 2
= 3x − 2x , Gọi x là hoành độ tiếp điểm. 0
Vì tiếp tuyến song song với đường thẳng y = 5x + 5 nên x = 1 − 0  f ′( x ) 2
= 5 ⇔ 3x − 2x = 5 ⇔ 0 0 0 5 x = 0  3
+ Với x = −1 ⇒ y = 0 , ta có pttt: y = 5( x + ) 1 = 5x + 5 (loại) 0 0 5 104  5  104 121 + Với x = ⇒ y =
, ta có pttt: y = 5 x −  + = 5x − . 0 0 3 27  3  27 27
Câu 43: Trong các dãy số (u sau, hãy chọn dãy số tăng? n ) A. n u = − . n B. 1 u = . C. u = − n D. u = . n n ( ) 1 . n n n n Hướng dẫn giải Chọn D.
Ta có: u = n ⇒ u = n +1 n n 1 + Xét hiệu u − u = n + − n = > n
∀ ∈ ℕ ⇒ Dãy số tăng. + n ( ) * 1 1 0, n 1
Câu 44: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 19/22 Mã đề 483
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song. Hướng dẫn giải Chọn B.
Câu A sai vì: Hai đường thẳng cùng vuông góc với một mặt phẳng có thể trùng nhau. Câu B đúng.
Câu C sai vì : Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng có thể chéo nhau.
Câu D sai vì : Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng có thể cắt nhau. 2 Câu 45: 2n − 3
Cho dãy số (u xác định bởi công thức số hạng tổng quát u =
với n ≥ 1, tìm số hạng n ) n n thứ ba của dãy số.
A. u = 5. B. u = 15. C. u = 4.
D. u = 3. 3 3 3 3 Hướng dẫn giải Chọn A. 2 2 2n − 3 2.3 − 3 Ta có: u = ⇒ u = = 5. n 3 n 3
Câu 46: Tính đạo hàm của hàm số: y = x tan 2x A. 2x x tan 2x + . B. tan 2x + . 2 cos x 2 cos 2x C. 2x 2
2x tan 2x + tan 2x + 2x . D. . 2 cos 2x Hướng dẫn giải Chọn C.
y = x tan 2x ⇒ y = ( x)) tan 2x + x ( tan 2x)′ ′ (2x)′ 2x 2 = tan 2x + x = tan 2x +
= 2x tan 2x + tan 2x + 2x . 2 2 cos 2x cos 2x
Câu 47: Cho hình chóp S.ABC có SA ⊥ (ABC) và tam giác ABC không vuông. Gọi H , K lần lượt là
trực tâm các tam giác ABC và tam giác SBC . Khẳng định nào sau đây đúng?
A. AH , SK , CB đồng phẳng.
B. AH , SK,CB đồng quy.
C. AH , SK , CB đôi một chéo nhau.
D. AH , SK , CB đôi một song song. Hướng dẫn giải Chọn B
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 20/22 Mã đề 483 S K C A H I B
Trong ( ABC) gọi I là giao điểm AH và BC
BC ⊥ SA (SA ⊥ ABC) và BC ⊥ AI ( Vì H là trực tâm tam giác ABC ) ⇒ BC ⊥ (SAI) ⇒ BC ⊥ SI
Mà BC ⊥ SK suy ra SK đi qua I
Vậy AH , SK , CB đồng quy Câu 48: a 3
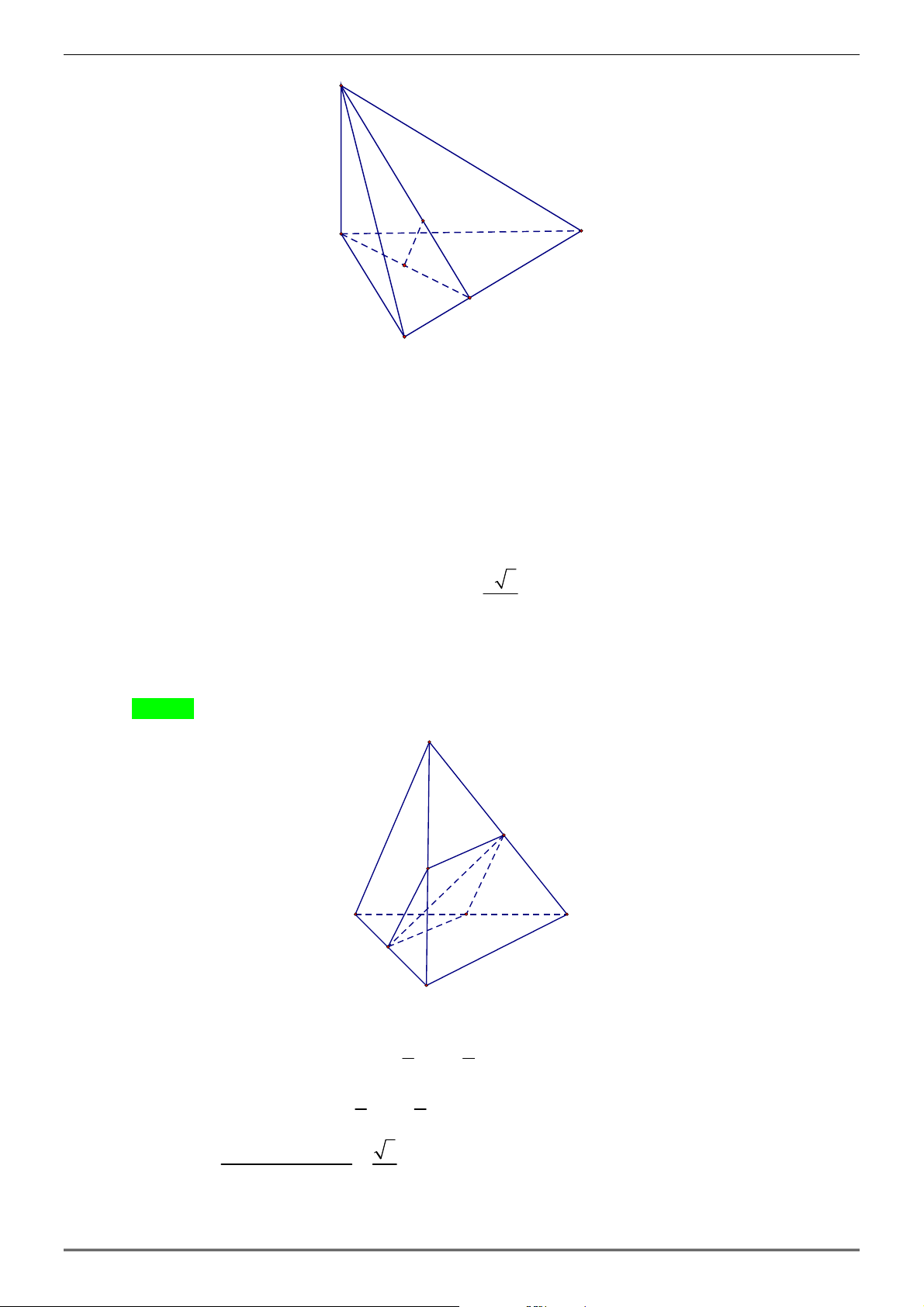
Cho tứ diện ABCD có AB = CD = a , IJ =
.Gọi I , J lần lượt là trung điểm của BC 2
và AD . Tính số đo góc giữa hai đường thẳng AB và CD A. 0 90 . B. 0 45 . C. 0 60 . D. 0 30 . Hướng dẫn giải Chọn C A J M N B D I C
Gọi M là trung điểm AC , N là trung điểm DB 1 a
Ta có IN / /CD / / JM , IN = JM = CD = 2 2 1 a
IM / / AB / / JN , IM = JN = AB = 2 2 2 2 2
MI + IJ − MJ 3 0 cosMIJ = = ⇒ MIJ = 30 2MI.IJ 2 0
⇒ MIN = 2MIJ = 60 ( MINJ là hình thoi)
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 21/22 Mã đề 483
( AB,CD) = (IM , IN ) 0 = MIN = 60
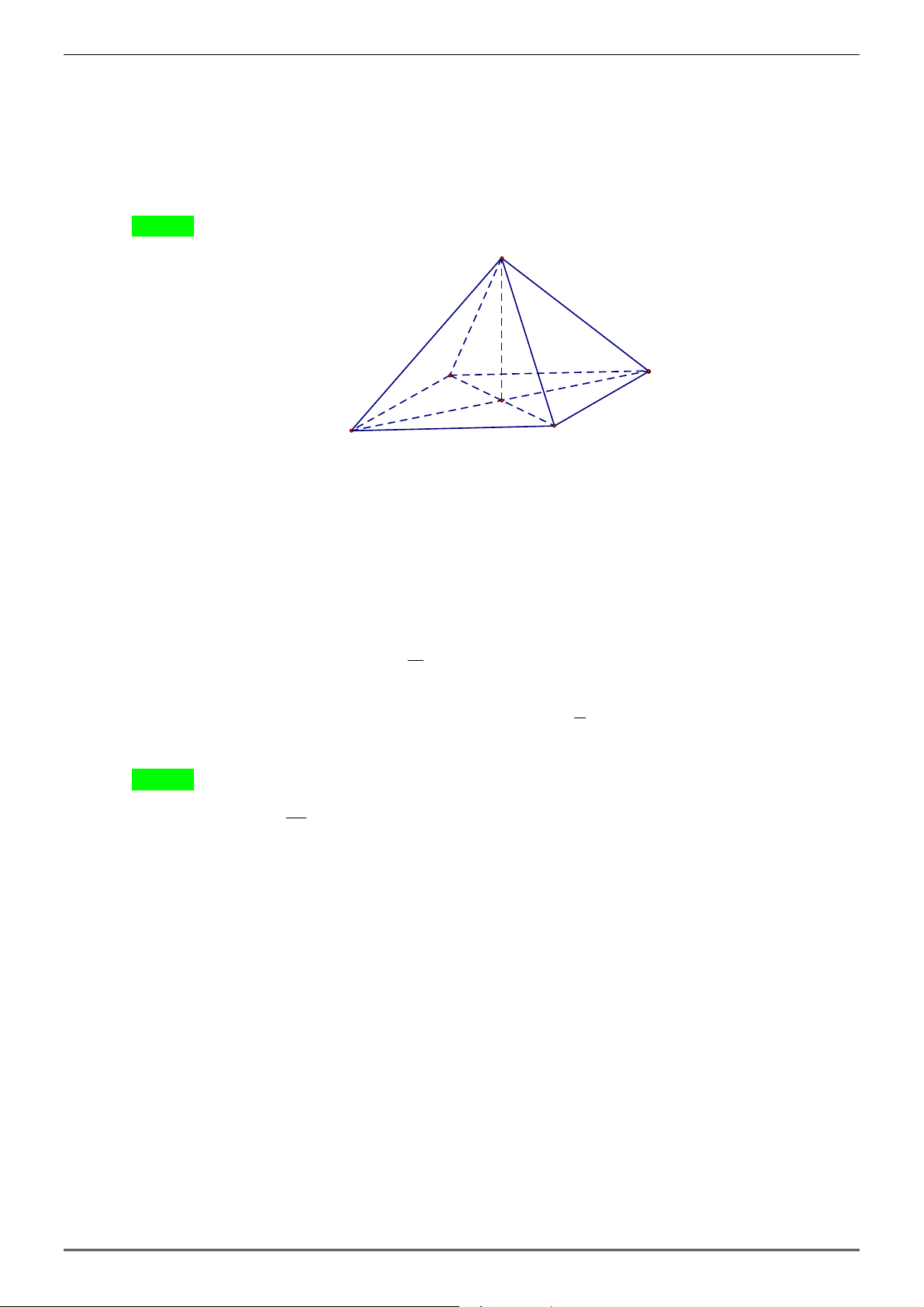
Câu 49: Cho hình chóp SABCD có ABCD là hình thoi tâm O và SA = SC, SB = SD . Trong các khẳng
định sau khẳng định nào sai?
A. AC ⊥ SA .
B. SA ⊥ BD .
C. AC ⊥ BD .
D. SD ⊥ AC . Hướng dẫn giải Chọn A S A D O B CSO ⊥ AC
Ta có: SO ⊥ BD
⇒ SO ⊥ (ABCD)
Từ đây ta chứng minh được AC ⊥ (SBD) ⇒ AC ⊥ SD
Từ đây ta chứng minh được BD ⊥ (SAC) ⇒ BD ⊥ SA
Câu C hiển nhiên đúng do ABCD là hình thoi 1
Câu 50: Cho cấp số nhân (u ) với u = − u = 3
− 2 .Tìm công bội q của cấp số nhân trên? n 1 2 7 A. q = ±1. B. q = ±4 . C. 1 q = ± . D. q = ±2 . 2 Hướng dẫn giải Chọn D −1 . 6 6 6
u = u q ⇔ −32 =
q ⇔ q = 64 ⇔ q = ±2 . 7 1 2
TOÁN HỌC BẮC–TRUNG–NAM sưutầmvàbiêntập Trang 22/22 Mã đề 483