Đề thi HK2 Toán 11 năm học 2016 – 2017 trường THPT Hai Bà Trưng – TT. Huế

SỞ GIÁO DỤC VÀ ĐẠO TẠO
ĐỀ KIỂM TRA HỌC KỲ 2 NĂM HỌC 2016 - 2017
TRƯỜNG THPT HAI BÀ TRƯNG MÔN: TOÁN 11
Thời gian làm bài: 90 phút ĐỀ CHÍNH THỨC
Họ và tên thí sinh: ........ TOANMATH.com .......... SBD: ...............................................
Lớp: ......................................................................... Phòng thi: .......................................
------------------------------------------------------------------------------------------
(Thí sinh không được sử dụng tài liệu khi làm bài) I. TRẮC NGHIỆM Câu 1:
Trong không gian, mệnh đề nào sau đây đúng?
A. Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau hoặc trùng nhau.
B. Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng song song.
C. Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng trùng nhau.
D. Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau. Hướng dẫn giải Chọn A.
Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau hoặc trùng nhau. Câu 2:
Cho tứ diện OABC có O , A O ,
B OC đôi một vuông góc. Khẳng định nào sau đây đúng?
A. Tam giác ABC là tam giác vuông.
B. Tam giác ABC có ba góc nhọn.
C. Tam giác ABC có một góc tù và hai góc nhọn. D. Tam giác ABC là tam giác đều. Hướng dẫn giải Chọn B. Câu 3:
Cho hình chóp S.ABC có SA  SB  SC  , a ASB  BS .
C Khẳng định nào sau đây đúng?
A. SA  B . C
B. SC  A . B
C. SB  A . C
D. SA  S . C Hướng dẫn giải Chọn C. S . B AC  S .
B SC  SA  S . B SC  S . B SA  S . B S .
C cos BSC  SB.SA.cos ASB 2
 SA cosBSCcosASB  0  SB  AC Câu 4:
Xét chuyển động có phương trình: s(t)  Asin( t  ), với ,
A , là những hằng số. Tìm gia
tốc tức thời tại thời điểm t của chuyển động.
A.  (t)  A cos( t). B. 2
 (t)  A sin( t).
C.  (t)  A2 sin( t).
D.  (t)  A cos( t). Hướng dẫn giải Chọn C.
s '(t)  At  'cost    A cost   Gia tốc 2
 (t)  s'(t)  At '.sint   A sint . Câu 5:
Trong không gian, mệnh đề nào sau đây đúng?
A. Nếu hai đường thẳng vuông góc với nhau thì hai đường thẳng đó cắt nhau.
B. Nếu hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
C. Nếu hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì hai đường thẳng đó vuông góc với nhau.
D. Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với đường thẳng này thì
cũng vuông góc với đường thẳng kia. Hướng dẫn giải Chọn D. Câu 6: Cho tứ diện ABC .
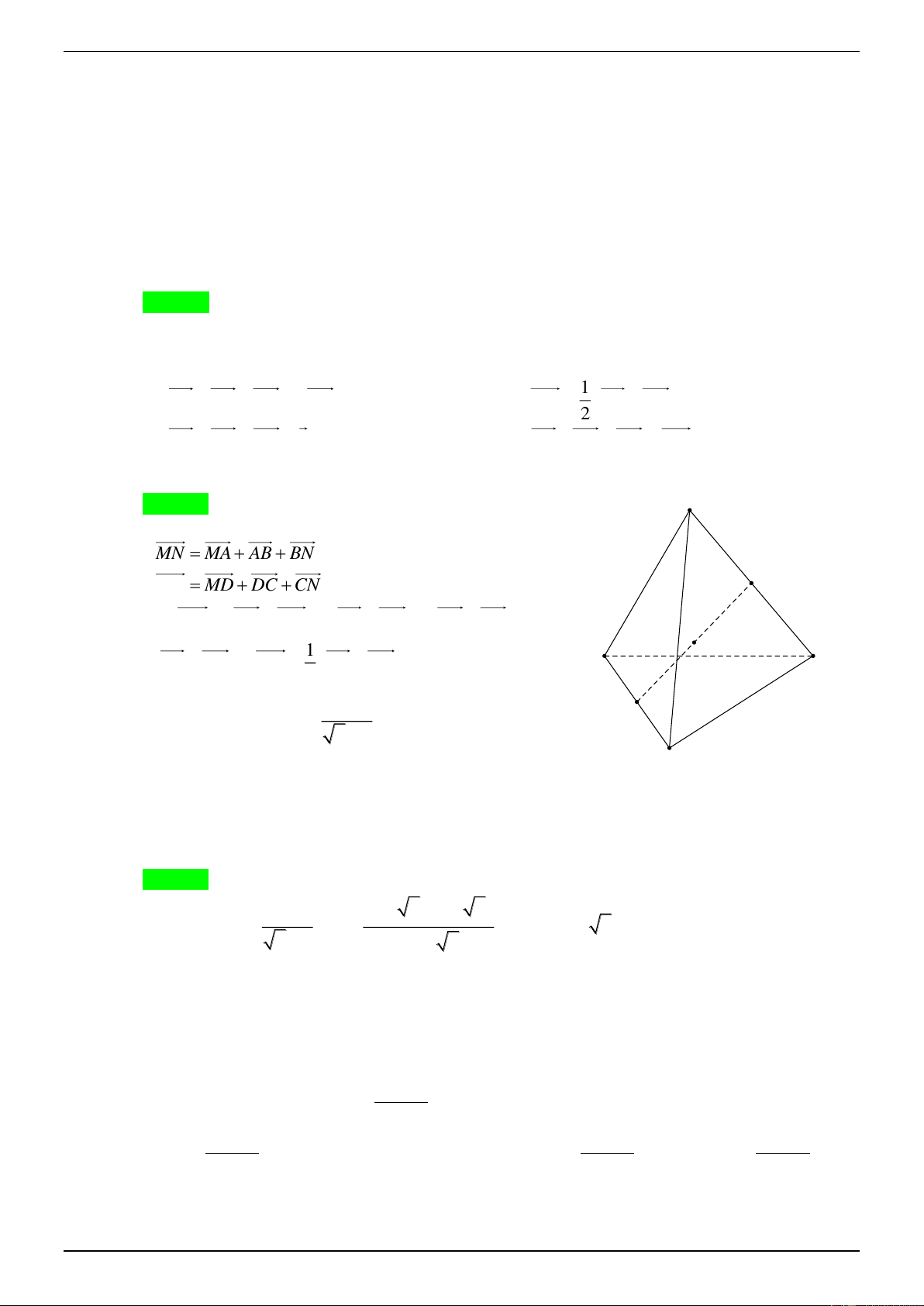
D Gọi M , N lần lượt là trung điểm của các cạnh A ,
D BC và G là trung
điểm MN. Mệnh đề nào sau đây đúng? 1
A. AB  AC  AD  3A . G B. MN  ABDC. 2
C. AB  AC  AD  0.
D. AB  AC  AD  MN. Hướng dẫn giải A Chọn B.
MN  MA AB  BN  M
MN  MD  DC  CN
2MN MAMDABDCBNCN 1 G
 AB  DC  MN  AB  DC. B D 2  4  x  khi x  4 N Câu 7:
Cho hàm số f (x)   x  2 . Tìm a để
ax 8 khi x  4 C
hàm số liên tục trên toàn trục số. A. a  1.  B. a  3.  C. a  2.  D. a  4.  Hướng dẫn giải Chọn B.  2 x2 4 x x 
lim f (x)  lim  lim    x   x x x  2 x 2 x lim 2  4. 4 4 4 x 4 
f (4)  4a  8
Hàm số liên tục với mọi x  4 và x  4  Hàm số liên tục trên toàn trục số
 Hàm số liên tục tại x  4  lim f (x)  f (4)  4a 8  4   a  3  . x 4  2 1 Câu 8:
Tính đạo hàm của hàm số  x y  . 1 x 1 2 1 A. y '  . y '   . '   . 2 (1 B. y '  2. C. D. y  x) 2 (1 x) 2 (1 x) Hướng dẫn giải Chọn D. ' '
Áp dụng công thức đạo hàm nhanh  ax  b  ad  bc  2  x 1 1       2   2  cx  d  (cx  d)  x 1  (1 x) Câu 9:
Trong không gian, mệnh đề nào sau đây đúng?
A. Nếu a (P) và b  (P) thì b  . a
B. Nếu a (P) và b a thì b (P).
C. Một đường thẳng vuông góc với hai đường thẳng phân biệt trong mp (P) thì nó vuông góc với mp (P).
D. Nếu a (P) và b  a thì b  (P). Hướng dẫn giải Chọn A.
Tính chất 3 SGK HH11 CB trang 101.  x  Câu 10: Tính 3 1 lim . x x  2 1 A. 3.  B. .  C. .  D.  . 2 Hướng dẫn giải Chọn A. 1 3   C1: 3  x 1 x 3 lim  lim    3  . x x  2 x 2 1 1 x C2: Casio 2 x  2x 1 Câu 11: Tìm lim . x 2x 1 1 1 A.  . . 2 B. 2 C. 1. D. 1.  Hướng dẫn giải Chọn A.  2 1 2  x     1  2 | x | 1 1  C1: x  2x 1 x x x   1 lim  lim lim   . x 2x 1 x  1  x  1  2 x 2  x 2       x   x  .  C2: Casio
2  4  6 . . 2n Câu 12: Tìm lim . 2 x n  n A. 2. B. 1. C. 0. D. Hướng dẫn giải Chọn B.
C1: Áp dụng công thức tổng n
n số hạng đầu của một cấp số cộng: S    u ta có: n n  2 u1 n 2  1   n 1 (2 2n)   
2  4  6  ...  2n 2  n  lim  lim  lim 1. 2 2 x  x  x n n n n  2  1  n 1    n  C2: Casio nhập
ta được kết quả là 1
Câu 13: Tìm tất cả các giá trị thực của m để phương trình 3 (
m x 1) (x  2)  2x  3  0 vô nghiệm. A. m   . B. m  1.
C. Không có giá trị .
m D. m  0. Hướng dẫn giải Chọn A. C1: Gọi 3 f (x)  (
m x 1) (x  2)  2x  3 xác định và liên tục trên . f (1)  1
 , f (2) 1 f (1). f (2)  0 m
   phương trình luôn có nghiệm m   .
C2: Dùng chức năng Shift solve của Casio .  3 2 3 x  2 x 1 Câu 14: Tìm lim .  2 x 1  (x 1) 1 A. 0. B. 9. C. D. . 9 Hướng dẫn giải Chọn D.
Casio: Thay x  0,999 vào ta được kết quả là 0.  x Câu 15: Cho hàm số 1 y 
, a, b là hằng số và a  b  0. Mệnh đề nào sau đây đúng? a  b 1 1 A. dy   d . x B. dy  d . x 2 1 x
2(a  b) 1 x 1 1 C. dy   d . x D. dy   d . x (2a  2 ) b 1 x
(a  b) 1 x Hướng dẫn giải Chọn C.  x' 1 (1 x) ' 1 y '     a  b
2(a  b) 1 x
(2a  2b) 1 x
Câu 16: Cho hàm số y  f (x) xác định trên ( ;
a b) và x0 (a; )
b . Giả sử các giới hạn (hữu hạn) sau đây
tồn tại, giới hạn nào là đạo hàm của hàm số y  f (x) tại điểm x0 ?
f (x)  f (x ) y  y
f (x)  f (x ) A. 0 lim . B. lim . C. lim . D. 0 lim . x      x  0 x x  0 x x x x 0 x x x 0 0 x Hướng dẫn giải Chọn A.
Theo định nghĩa đạo hàm, SGK ĐS & GT 11 CB trang 48.
Câu 17: Tìm mệnh đề đúng trong các mệnh đề sau:
A. Nếu hình hộp có bốn đường chéo bằng nhau thì nó là hình lập phương.
B. Nếu hình hộp có có hai mặt là các hình vuông thì nó là hình lập phương.
C. Nếu hình hộp có sáu mặt bằng nhau thì nó là hình lập phương.
D. Nếu hình hộp có ba mặt chung một đỉnh là các hình vuông thì nó là hình lập phương. Hướng dẫn giải Chọn D.
Vì các mặt đối diện của hình hộp bằng nhau nên nếu hình hộp có ba mặt chung một đỉnh là các
hình vuông thì nó có 6 mặt là hình vuông. Do đó, hình hộp đã cho là hình lập phương. n2 2  5 Câu 18: Tìm lim . 3n  2.5n 5 5 25 1 A.  . B. . C.  . D.  . 2 2 2 2 Hướng dẫn giải Chọn C. n  1   n2 2 25 n   C1: 2  5 2  25.5  5  25 lim  lim  lim   . 3n  2.5n 3n  2.5n n 2  3   2    5  C2: Nhập
Câu 19: Cho các hàm số y  sin , x y  cos , x y  tan ,
x y  cot x có đạo hàm trên tập xác định của nó.
Mệnh đề nào sau đây sai? 1 1
A. tan x'  .
B. sin x'  cos . x
C. cos x'  sin . x
D. cot x'  . 2 cos x 2 sin x Hướng dẫn giải Chọn D.  x 1 cot '   . 2 sin x
Câu 20: Cho hình hộp chữ nhật ABC .
D A' B'C ' D' có AB  , a AD  , b AA'  .
c Khẳng định nào sau đây sai? A B C D
A. Khoảng cách giữa đường thẳng AB và mp ( ' ' ' ') bằng . a
B. Khoảng cách giữa đường thẳng AC và mp B 'C ' bằng c.
C. Khoảng cách giữa đường thẳng AD và mp (A' B'C ' D' ) bằng c.
D. Khoảng cách từ điểm A và mp (CDC') bằng b.
(A'B'C'D') Hướ A ng dẫn giải b D Chọn A. a d(A ,
B (A' B'C ' D')  d( ,
A (A' B'C ' D')) B  C AA'  . c c A' D' B'
Câu 21: Tính đạo hàm của hàm số 1 C' y  . x x 3 3 1 3 x A. y'   . B. y '   . x C. y'  . D. y'   . 2 2x x 2 x 2 Hướng dẫn giải Chọn A.  ' 1 3 x  . 1 x 2 x x x x 3 2 y   y'         x x   . 2 3 3 2 x x 2x x x x
Câu 22: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh SA vuông góc với đáy và SA  . a
Tính góc giữa mp (SBC) và mp (SDC). A. 0 120 . B. 0 30 . C. 0 90 . D. 0 60 . Hướng dẫn giải Chọn D. S
Tam giác SBC bằng tam giác SCD ( . c .
c c) nên hai đường
cao tương ứng BH và DH cùng đi qua một điểm H trên
cạnh SC và BH  CH
BC  (SAB) nên S  BC vuông tại H a S . B BC a 2.a a 2 B  BH    2 2 2 2 A D SB  BC 2a  a 3 2 2 2a 2a 2 2 2 2   2   3 3 a B a BH DH BD 1 C cos BHD     2 2BH.DH 2a 2 2. 3 0  BHD 120  SBC SCD  0 0 ( ),(
)  (BH,DH) 180  BHD  60
Câu 23: Cho hàm số f ( ) x  (
x x 1)(x  2)(x  3)(x  4). Tính f '(0). A. 24.  B. 24. C. 42. D. 0. Hướng dẫn giải Chọn B. Casio: Nhập
Câu 24: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi A', B', C ', D' lần lượt là trung điểm của các cạnh S , A S , B SC và .
SD Tìm mệnh đề đúng trong các mệnh đề sau đây.
A. A'C ' (SB ) D .
B. A'B' (SA ) D .
C. (A'C ' D') (ABC). D. A'C ' B . D Hướng dẫn giải Chọn C. ( S
A'C ' D')  (A'B'C'D') (ABC ) D  (ABC). A' D' B' C' A D B C
Câu 25: Tính đạo hàm của hàm số 2 y  sin 2 . x A. 2 y '  cos 2 . x
B. y '  2sin 4 . x C. 2 y '  2cos 2 . x
D. y '  2sin 2 . x Hướng dẫn giải Chọn B. y '  2sin 2 .
x sin 2x'  2sin 2 .
x 2x'.cos 2x  2.2sin 2 .
x cos 2x  2sin 4 . x II. TỰ LUẬN.
Bài 1: (1,5 điểm) Cho hàm số y  f (x)  3 sin x  cos x (C). 
a) Viết phương trình tiếp tuyến của đồ thị hàm số (C) tại điểm có hoành độ x  . 2
b) Giải phương trình f '(x)  0.
c) Chứng minh rằng y  y'  0. Hướng dẫn giải
y '  3 cos x  sin ,
x y '   3 sin x  cos . x            a) x  , y
 3sin  cos  3, y'  3cos  sin      1. 2  2  2 2  2  2 2 
Phương trình tiếp tuyến của đồ thị hàm số (C) tại điểm có hoành độ x  là: 2     y  1 x   3  x     3.  2  2 
b) f '(x)  0  3cos x  sin x  0  3  tan x  0  tan x   3  x     3 k
c) Ta có y  y'   3sin x cosx 3sin x cosx  0 (đpcm).
Bài 2: (1 điểm) Cho hình chóp S.ABCD có đáy là hình vuông cạnh , a SA  (ABC ) D , SA  2 . a
a) Chứng minh rằng (SC ) D  (SA ) D .
b) Tính khoảng cách từ điểm B đến mp (SCD). Hướng dẫn giải S   a) Ta có CD AD   CD  (SAD) C  D  SA H mà CD  (SC ) D  (SC ) D  (SAD).
b) Vì AB CD nên AB (SC ) D  d( , B (SC ) D )  d( , A (SC ) D ) 2a   Kẻ AH SD
AH  SD tại H    AH  (SCD) A  D AH  CD S . A AD 2 . a a  d( ,
A (SCD))  AH   2 2 2 2 B SA  AD (2a)  a a C 2a   d(B,(SCD)). 5
Document Outline

• Untitled