SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II NĂM HỌC 2018-2019 QUẢNG NAM
Môn: TOÁN – Lớp 11
Thời gian: 60 phút (không kể thời gian giao đề) ĐỀ CHÍNH T HỨC MÃ ĐỀ 101
(Đề gồm có 02 trang) A
/ TRẮC NGHIỆM: (5,0 điểm)
Câu 1. Trong các mệnh đề sau, mệnh đề nào sai ?
A. Nếu 𝑎𝑎//𝑏𝑏 và (𝛼𝛼)⊥ a thì (𝛼𝛼)⊥ b .
B. Nếu (𝛼𝛼)//(𝛽𝛽) và a⊥ (𝛼𝛼) thì a⊥(𝛽𝛽) .
C. Nếu a và b là hai đường thẳng phân biệt và a ⊥ (𝛼𝛼) , b⊥(𝛼𝛼) thì 𝑎𝑎//𝑏𝑏 .
D. Nếu 𝑎𝑎//(𝛼𝛼) và b⊥ a thì b ⊥(𝛼𝛼) .
Câu 2. Tìm đạo hàm của hàm số y = 3cosx +1.
A. 𝑦𝑦′ = 3 sin 𝑥𝑥.
B. 𝑦𝑦′ = −3 sin 𝑥𝑥 + 1.
C. 𝑦𝑦′ = −3 sin 𝑥𝑥.
D. 𝑦𝑦′ = − sin 𝑥𝑥. 2 Câu 3. Tính x + 3x − 4 lim . x 1− → x −1 A. 5. B. 0. C. +∞. D. −5. 3
 ax +1 − 1− bx Câu 4. Cho hàm số  khi x ≠ 0
y = f (x) =  x . 3
 a −5b −1 khi x = 0
Tìm điều kiện của tham số a và b để hàm số trên liên tục tại điểm x = 0.
A. 2𝑎𝑎 − 6𝑏𝑏 = 1.
B. 2𝑎𝑎 − 4𝑏𝑏 = 1.
C. 16𝑎𝑎 − 33𝑏𝑏 = 6.
D. 𝑎𝑎 − 8𝑏𝑏 = 1. Câu 5. Cho hàm số 2
y = sin x . Mệnh đề nào dưới đây đúng ?
A. 4𝑦𝑦. 𝑐𝑐𝑐𝑐𝑐𝑐2𝑥𝑥 − (𝑦𝑦′)2 = −2𝑐𝑐𝑠𝑠𝑠𝑠22𝑥𝑥.
B. 4𝑦𝑦. 𝑐𝑐𝑐𝑐𝑐𝑐2𝑥𝑥 − (𝑦𝑦′)2 = 0.
C. 2𝑐𝑐𝑠𝑠𝑠𝑠𝑥𝑥 − 𝑦𝑦′ = 0.
D. 𝑐𝑐𝑠𝑠𝑠𝑠2𝑥𝑥 + 𝑦𝑦′ = 1.
Câu 6. Cho hình chóp S.ABCD có SA ⊥ (ABCD) và đáy ABCD là hình vuông. Mệnh đề nào dưới đây đúng?
A. (𝑆𝑆𝑆𝑆𝑆𝑆)⊥(𝑆𝑆𝑆𝑆𝑆𝑆). B. (𝑆𝑆𝑆𝑆𝑆𝑆)⊥(𝑆𝑆𝑆𝑆𝑆𝑆). C. 𝑆𝑆𝑆𝑆⊥(𝑆𝑆𝑆𝑆𝑆𝑆). D. 𝑆𝑆𝑆𝑆⊥(𝑆𝑆𝑆𝑆𝑆𝑆).
Câu 7. Tìm vi phân của hàm số 2
y = 3x − 2x +1.
A. 𝑑𝑑𝑦𝑦 = 6𝑥𝑥 − 2. B. 𝑑𝑑𝑦𝑦 = (6𝑥𝑥 − 2)𝑑𝑑𝑥𝑥. C. 𝑑𝑑𝑥𝑥 = (6𝑥𝑥 − 2)𝑑𝑑𝑦𝑦. D. 𝑑𝑑𝑦𝑦 = 6𝑥𝑥 − 2𝑑𝑑𝑥𝑥.
Câu 8. Một chất điểm chuyển động theo phương trình 3 2
S = t + 5t − 5 , trong đó t > 0, t được tính
bằng giây (s) và S được tính bằng mét (m) . Tính vận tốc của chất điểm tại thời điểm t = 2 ( giây) .
A. 32 𝑚𝑚/𝑐𝑐.
B. 22 𝑚𝑚/𝑐𝑐.
C. 27 𝑚𝑚/𝑐𝑐.
D. 28 𝑚𝑚/𝑐𝑐. Câu 9. Tính x + 5 lim . x→4 x −1 A. 3. B. 1. C. −5. D. +∞. a Câu 10 3
. Cho hình chóp tứ giác đều S.ABCD có AB = a và 𝑆𝑆𝑆𝑆 =
. Tính khoảng cách từ A đến 2 mặt phẳng (SBC). a a A. 2
𝑑𝑑�𝑆𝑆; (𝑆𝑆𝑆𝑆𝑆𝑆)� = 4 .
B. 𝑑𝑑�𝑆𝑆; (𝑆𝑆𝑆𝑆𝑆𝑆)� = 2. a C. 2
𝑑𝑑�𝑆𝑆; (𝑆𝑆𝑆𝑆𝑆𝑆)� = 𝑎𝑎.
D. 𝑑𝑑�𝑆𝑆; (𝑆𝑆𝑆𝑆𝑆𝑆)� = 2 . Trang 1/2 – Mã đề 101
Câu 11. Cho tứ diện ABCD , gọi G là trọng tâm của tam giác BCD . Mệnh đề nào dưới đây đúng? A. GA
���⃗ + 𝐺𝐺��𝑆𝑆�⃗ + 𝐺𝐺�𝑆𝑆 ��⃗ = 𝑂𝑂�⃗. B. GA
���⃗ + 𝐺𝐺�𝑆𝑆
��⃗ + 𝐺𝐺��𝑆𝑆�⃗ = 𝑂𝑂�⃗. C. GA
���⃗ + 𝐺𝐺�𝑆𝑆
��⃗ + 𝐺𝐺�𝑆𝑆 ��⃗ = 𝑂𝑂�⃗. D. GB
���⃗ + 𝐺𝐺��𝑆𝑆�⃗ + 𝐺𝐺�𝑆𝑆 ��⃗ = 𝑂𝑂�⃗. Câu 12. Tính 5n +1 lim . 3n + 7 A. 5. B. 5. C. 1 . D. 7 3 7 0.
Câu 13. Tìm đạo hàm cấp 2 của hàm số 1 y = . x + 2 − − A. 2 2 1 1 𝑦𝑦′′ = 3 ( . B. 𝑦𝑦′′ = . C. 𝑦𝑦′′ = . D. 𝑦𝑦′′ = . x + 2) 3 (x + 2) 2 (x + 2) 3 (x + 2)
Câu 14. Cho hình lập phương ABCD.A'B'C 'D'. Gọi α là góc giữa hai đường thẳng A'B và CB'. Tính α .
A. 𝛼𝛼 = 300. B. 𝛼𝛼 = 450. C. 𝛼𝛼 = 600. D. 𝛼𝛼 = 900.
Câu 15. Tìm đạo hàm của hàm số 3
y = x − 2x .
A. 𝑦𝑦′ = 3𝑥𝑥 − 2. B. 𝑦𝑦′ = 3𝑥𝑥2 − 2. C. 𝑦𝑦′ = 𝑥𝑥3 − 2. D. 𝑦𝑦′ = 3𝑥𝑥2 − 2𝑥𝑥.
B/ TỰ LUẬN: (5,0 điểm)
Bài 1 (2,0 điểm). + − a. Tìm 5 x 1 2 lim + n . b. Tìm lim . 4 − n x→3 x − 3 2  x − 7x +10 c. Cho hàm số  khi x ≠ 5
y = f (x) =  . x − 5 2m - 1 khi x = 5
Tìm điều kiện của tham số m để hàm số trên liên tục tại điểm x = 5.
Bài 2 (1,0 điểm). Cho hàm số 3 2
y = f (x) = x + x −1, có đồ thị (C ).
a. Tính đạo hàm của hàm số trên.
b. Viết phương trình tiếp tuyến của đồ thị (C ) tại điểm có hoành độ x =1. 0
Bài 3 (2,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a; các cạnh bên
của hình chóp cùng bằng 𝑎𝑎√3.
a. Chứng minh rằng 𝑆𝑆𝑆𝑆 ⊥ (𝑆𝑆𝑆𝑆𝑆𝑆).
b. Gọi (P) là mặt phẳng đi qua A và vuông góc với cạnh SC. Xác định thiết diện của hình chóp
S.ABCD cắt bởi mặt phẳng (P).
c. Tính góc giữa đường thẳng AB và mặt phẳng (P).
=================Hết=================
Họ và tên:……………….......…………………..SBD: …….......………….
Chú ý: Học sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm. Trang 2/2 – Mã đề 101
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KỲ II QUẢNG NAM
MÔN TOÁN 11 – NĂM HỌC 2018-2019
Thời gian làm bài: 60 phút (Không kể thời gian phát đề)
Gồm các mã đề 101; 104; 107; 110; 113; 116; 119; 122.
A. Phần trắc nghiệm: (5,0 điểm)
Mã 101 Mã 104 Mã 107 Mã 110 Mã 113 Mã 116 Mã 119 Mã 122 1. D 1. D 1. A 1. A 1. C 1. A 1. D 1. B 2. C 2. B 2. D 2. B 2. A 2. C 2. B 2. C 3. D 3. B 3. A 3. C 3. D 3. D 3. C 3. D 4. C 4. A 4. C 4. A 4. B 4. A 4. A 4. C 5. B 5. D 5. D 5. C 5. C 5. A 5. A 5. A 6. A 6. B 6. C 6. C 6. B 6. B 6. B 6. A 7. B 7. D 7. C 7. B 7. C 7. A 7. A 7. A 8. A 8. A 8. A 8. B 8. B 8. B 8. C 8. A 9. A 9. C 9. B 9. D 9. D 9. A 9. D 9. C 10. D 10. D 10. B 10. A 10. A 10. D 10. D 10. D 11. D 11. A 11. B 11. D 11. C 11. C 11. D 11. D 12. B 12. B 12. D 12. D 12. D 12. D 12. D 12. B 13. A 13. C 13. B 13. D 13. A 13. B 13. C 13. D 14. C 14. C 14. A 14. C 14. A 14. C 14. B 14. A 15. B 15. A 15. B 15. A 15. D 15. C 15. B 15. B
B. Phần tự luận: (5,0 điểm) Câu Nội dung Điểm 5 +1 5 + n n a) lim = lim 4 0,25 − n 4 −1 n = 1 − 0,25 x ( x+1−2)( x+1+ + − 2 1 2 ) lim = lim 0,25 b) x 3 → x − x 3 3 →
(x −3)( x +1+ 2) 1 1 ( 2đ) = lim = 1. 0,25 √𝑥𝑥+1+2 4 𝑥𝑥→3 2 x − 7x +10
(x − 2)(x − 5) lim f (x) = lim = lim = lim(x − 2) = 3 x→5 x→5 x→5 x − 5 x − 5 x→5 0,25 f(5) = 2m-1 0,25
c) f (x) liên tục tại x = 5 ⇔ lim f (x) = f (5) 0,25 x→5
⇔ 3 = 2m −1 ⇔ m = 2 0,25
Kết luận với m = 2 thì hàm số liên tục tại x = 5. a. ' 2
f (x) = 3x + 2x 0.25 Trang 1/2 Tính đúng: 0y =1 0,25 2
b. f (′x ) = f (1 ′ ) = 5 0,25 (1đ) 0
Phương trình tiếp tuyến cần tìm là y = 5x − 4 0,25
Bài 3 (2,0 điểm).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a; các cạnh bên của hình chóp cùng bằng 𝑎𝑎√3.
a. Chứng minh rằng 𝐵𝐵𝐵𝐵 ⊥ (𝑆𝑆𝑆𝑆𝑆𝑆).
b. Gọi (P) là mặt phẳng đi qua A và vuông góc với cạnh SC. Xác định thiết diện của hình
chóp S.ABCD cắt bởi mặt phẳng (P).
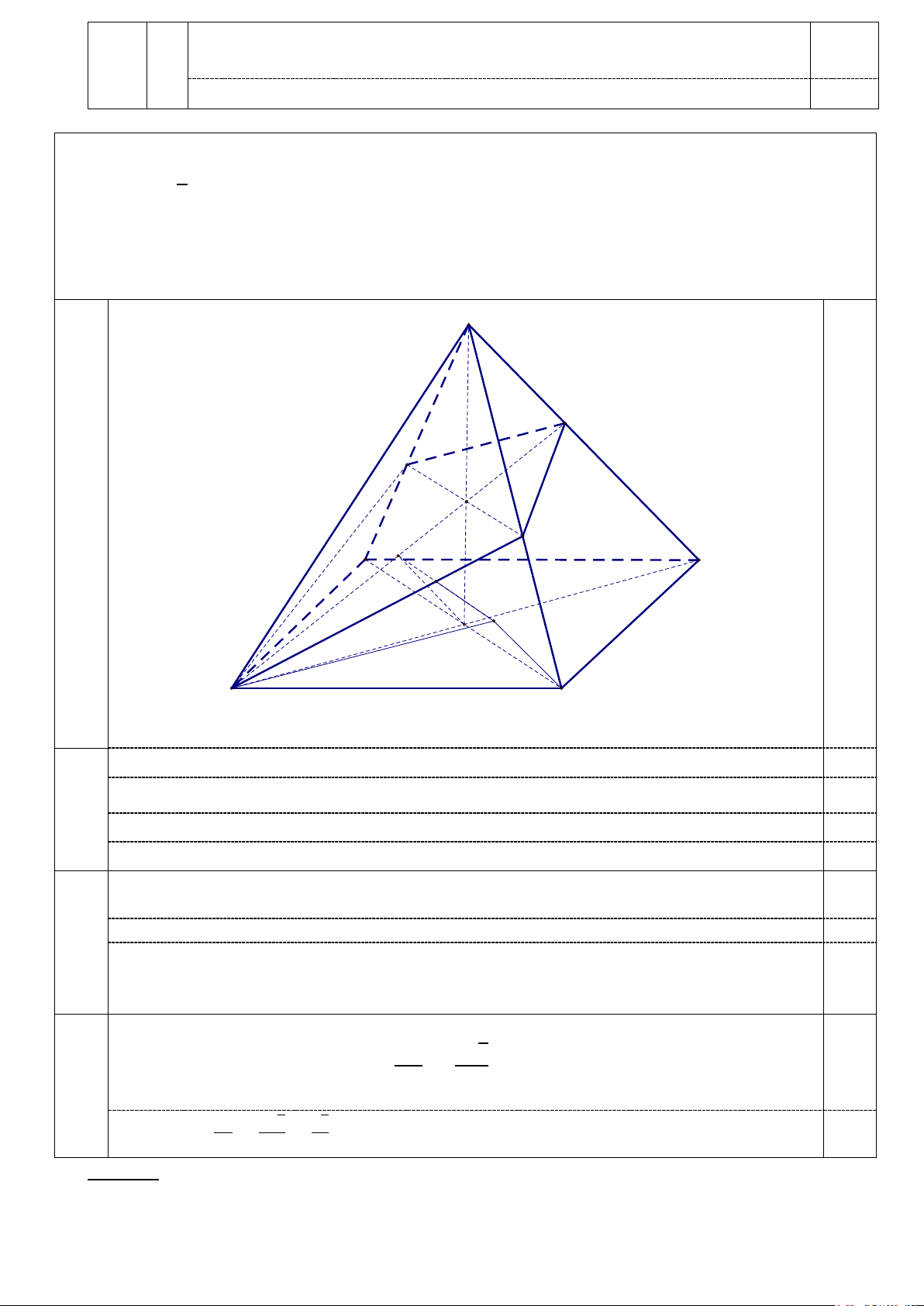
c. Tính góc giữa đường thẳng AB và mặt phẳng (P). S C' D' H 0,25 B' K D C F O A B
(Hình vẽ phục vụ câu a, đúng được 0,25 điểm).
Câu a) Chứng minh rằng 𝐵𝐵𝐵𝐵 ⊥ (𝑆𝑆𝑆𝑆𝑆𝑆).
a + 𝑆𝑆𝐵𝐵 = 𝑆𝑆𝐵𝐵 nên △ 𝑆𝑆𝐵𝐵𝐵𝐵 𝑐𝑐â𝑛𝑛 ⇒ 𝐵𝐵𝐵𝐵 ⊥ 𝑆𝑆𝑆𝑆. 0,75 0,25
+ 𝐵𝐵𝐵𝐵 ⊥ 𝑆𝑆𝑆𝑆 (gt) 0,25
𝑆𝑆𝑆𝑆 ⊂ (𝑆𝑆𝑆𝑆𝑆𝑆); 𝑆𝑆𝑆𝑆 ⊂ (𝑆𝑆𝑆𝑆𝑆𝑆). Vậy 𝐵𝐵𝐵𝐵 ⊥ (𝑆𝑆𝑆𝑆𝑆𝑆). 0,25
b. Gọi (P) là mặt phẳng đi qua A và vuông góc với cạnh SC. Xác định thiết diện của
b hình chóp S.ABCD cắt bởi mặt phẳng (P).
0,5 + Vì (𝑃𝑃) ⊥ 𝑆𝑆𝑆𝑆 nên hạ 𝑆𝑆𝑆𝑆′ ⊥ 𝑆𝑆𝑆𝑆 (𝑆𝑆′ ∈ 𝑆𝑆𝑆𝑆); 𝑆𝑆𝑆𝑆’⋂𝑆𝑆𝑆𝑆 = {𝐻𝐻} 0,25
+Vì 𝐵𝐵𝐵𝐵 ⊥ (𝑆𝑆𝑆𝑆𝑆𝑆) nên 𝐵𝐵𝐵𝐵 ⊥ 𝑆𝑆𝑆𝑆. Suy ra (𝑃𝑃) ∕∕ 𝐵𝐵𝐵𝐵 ⇒ (𝑃𝑃)⋂(𝑆𝑆𝐵𝐵𝐵𝐵) = 𝐵𝐵′𝐵𝐵′
với 𝐵𝐵′𝐵𝐵′//𝐵𝐵𝐵𝐵; 𝐵𝐵′ ∈ 𝑆𝑆𝐵𝐵, 𝐵𝐵′ ∈ 𝑆𝑆𝐵𝐵; 0,25
Vậy thiết diện cần tìm là tứ giác AB’C’D’(có hình vẽ đúng mới chấm).
Hạ 𝑆𝑆𝑂𝑂 ⊥ 𝑆𝑆𝑆𝑆′ (K∈ 𝑆𝑆𝑆𝑆′). Suy ra 𝑆𝑆𝑂𝑂 ⊥ (𝑃𝑃). c
0,5 Hạ 𝐵𝐵𝐵𝐵 ⊥ (𝑃𝑃) thì 𝐵𝐵𝐵𝐵 = 𝑆𝑆𝑂𝑂 = 𝐶𝐶𝐶𝐶′ = 𝑎𝑎√3 (vì d(B;(P)) = d(O; (P)). 0,25 2 6
Vậy góc giữa đường thẳng AB và mặt phẳng (P) là góc 𝐵𝐵𝑆𝑆𝐵𝐵 � .
𝑠𝑠𝑠𝑠𝑛𝑛𝐵𝐵𝑆𝑆𝐵𝐵
� = 𝐵𝐵𝐵𝐵 = 𝑎𝑎√3 = √3 . Vậy 𝐵𝐵𝑆𝑆𝐵𝐵 � = 16046′43,16′′. 0,25 𝐵𝐵𝐵𝐵 6𝑎𝑎 6
Ghi chú: - Học sinh giải cách khác đúng thì được điểm tối đa tương ứng.
- Tổ Toán mỗi trường cần thảo luận kỹ HDC trước khi tiến hành chấm.
--------------------------------Hết-------------------------------- Trang 2/2
Document Outline

• mã gốc 101
• ĐÁP ÁN ĐỀ GỐC 101