Đề thi hk2 toán 11 sở gd & đt quảng nam 2020-2021 có đáp án

SỞ GIÁO DỤC VÀ ĐÀO TẠO KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2020-2021 QUẢNG NAM
Môn: TOÁN – Lớp 11
Thời gian: 60 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
(Đề gồm có 03 trang) MÃ ĐỀ 108
A/ TRẮC NGHIỆM: (7,0 điểm)
Câu 1: Tìm đạo hàm của hàm số y  cot x với x  k , k   . 1 1 1 1 A. y '  . B. y '   . C. y '  . D. y '   . 2 sin x 2 sin x 2 cos x 2 cos x
Câu 2: Trong không gian, cho đoạn thẳng AB có trung điểm là M , () là mặt phẳng trung trực
của đoạn thẳng AB . Phát biểu nào sau đây đúng ?
A. () qua A và vuông góc với AB .
B. () qua M và không vuông góc với AB .
C. () qua B và vuông góc với AB .
D. () qua M và vuông góc với AB .
Câu 3: Cho hai hàm số u  u  x, v  v x có đạo hàm tại điểm x thuộc khoảng xác định. Mệnh
đề nào sau đây sai ? /  u  u ' A.    .
B. u  v'  u ' v ' .  v  v '
C. ku'  ku ' ( k là hằng số).
D. u  v'  u ' v ' .
Câu 4: Hàm số nào dưới đây liên tục trên toàn bộ tập số thực  ? 2x 1 x 1 A. y  . B. y  . C. 2 y  x  5 . x D. y  cot . x 2 x 1 2x 1
Câu 5: Trong không gian, cho hai đường thẳng phân biệt a,b và mặt phẳng () . Phát biểu nào sau đây đúng ?
A. Nếu a / /() và b  ( ) thì a  . b
B. Nếu a  () và b  ( ) thì a  . b
C. Nếu a / /() và b  a thì b  ( ).
D. Nếu a / /() và b / /() thì a  . b 3x  5 Câu 6: lim bằng  x1 x 1 A. .  B.   C. 5. D. 3
Câu 7: Tìm đạo hàm của hàm số y  3sin x .
A. y '  cos x . B. y '  3  cos x .
C. y '  3cos x .
D. y '   cos x .
Câu 8: Mệnh đề nào sau đây sai ? 1 A. lim  0.
B. lim c  c (c là hằng số) n 1 1 C. lim n
q  0 ( q  1) . D. lim  (k   .) k n k
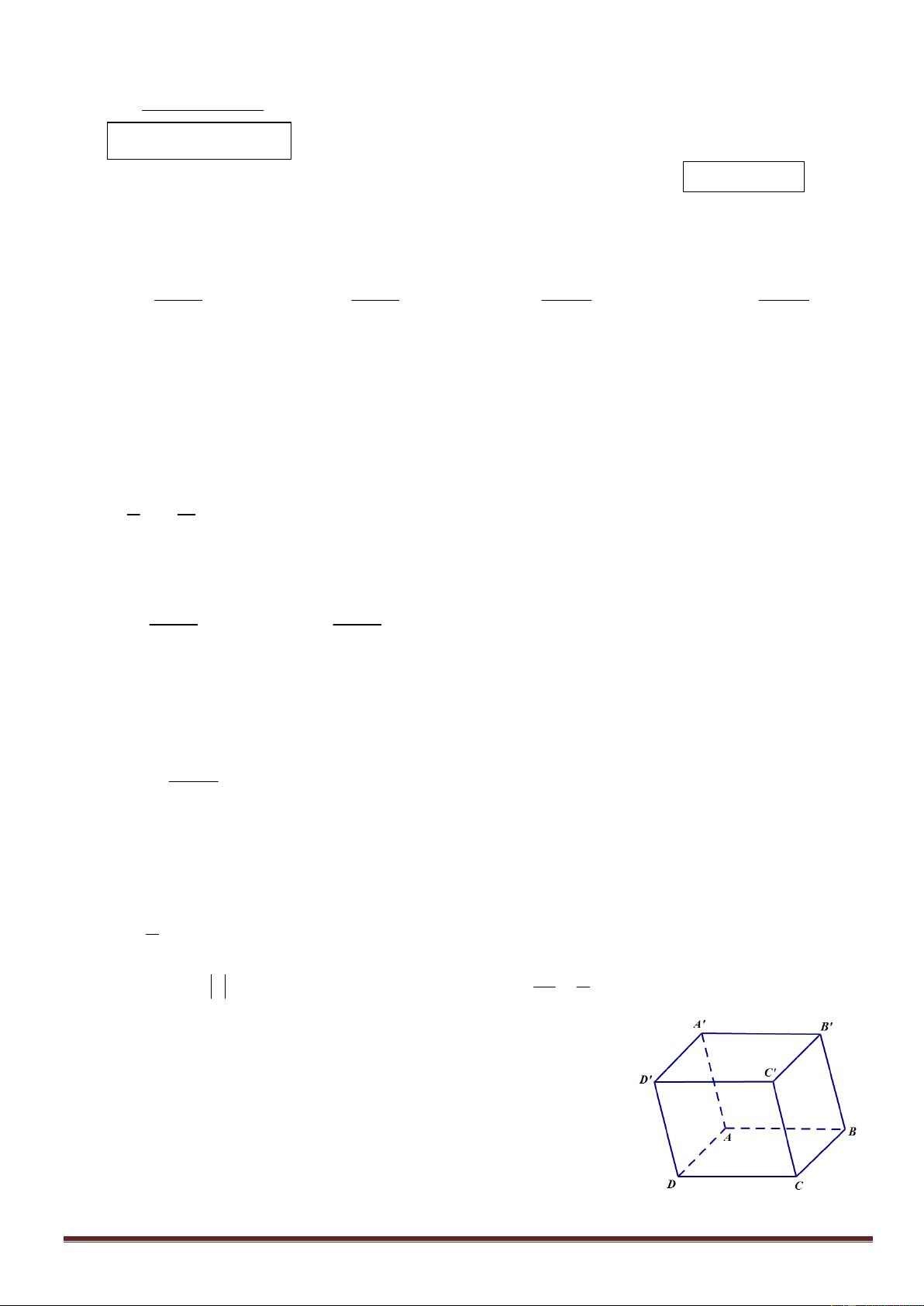
Câu 9: Cho hình hộp ABC .
D A' B'C ' D' (hình vẽ minh hoạ). Mệnh
đề nào sau đây đúng ? 
  
A. BD '  BA  BC  B . D 
  
B. BD '  BD  BC  BB '. 
  
C. BD '  BA  BC  BB '. 
  
D. BD '  BA  BD  BB '. Trang 1
Câu 10: Mệnh đề nào sau đây sai ? A.  / n x
 nx n , n   1 .
B. c/  0 ( c là hằng số).
C.  x/  1. D.  x / 1   x  0 . 2 x 
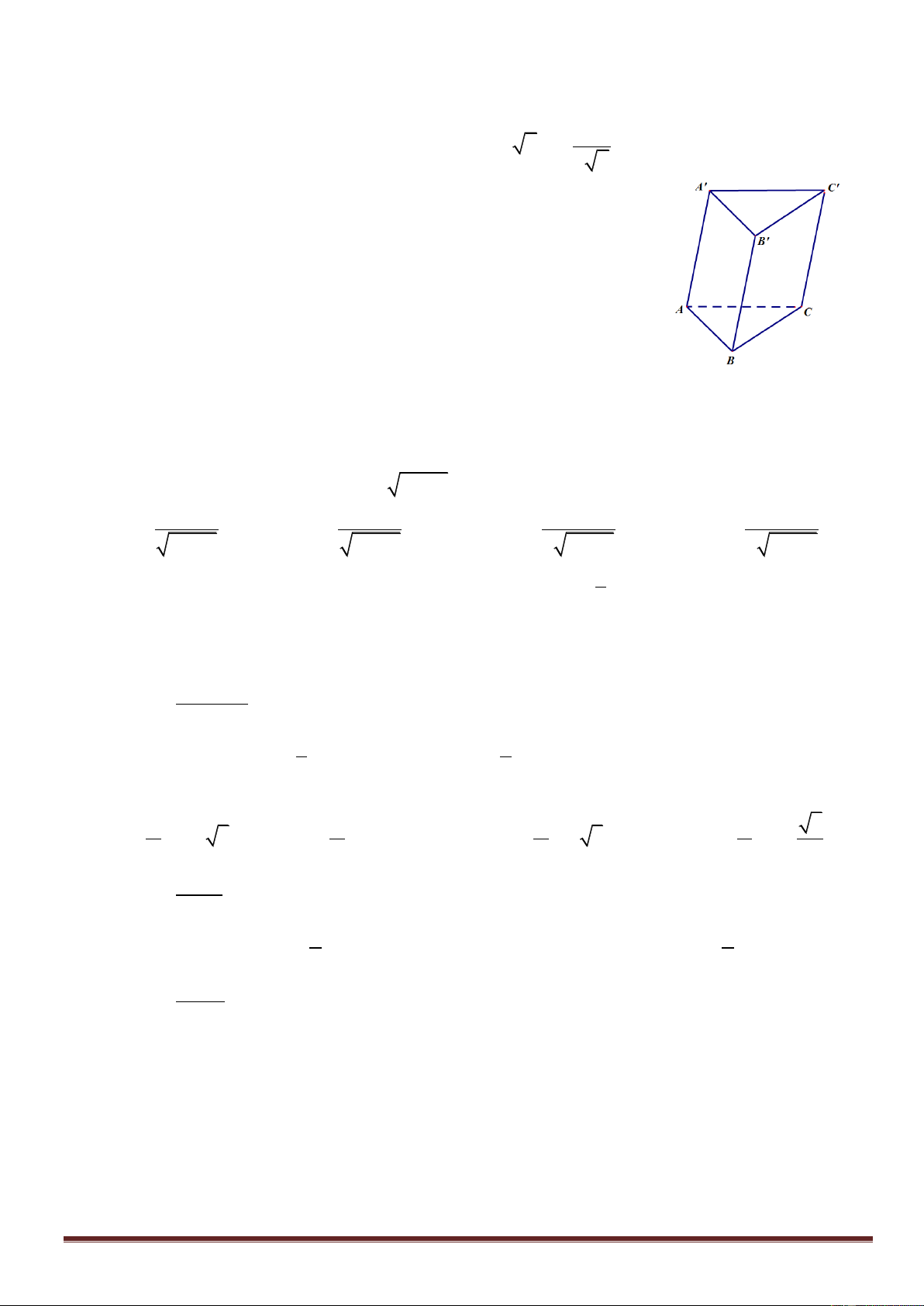
Câu 11: Cho lăng trụ AB .
C A' B'C ' (hình vẽ minh hoạ). Vectơ C 'C
không phải là vectơ chỉ phương của đường thẳng nào sau đây ? A. BB '. B. AA'. C. . AB D. CC '.
Câu 12: Cho hai hàm số f  x, g  x thỏa mãn lim f  x  3
 và lim g x  8. Giá trị của x 1  x 1 
lim  f  x  g  x   bằng x 1  A. 5. B. 11.  C. 11.  D. 5. 
Câu 13: Tìm đạo hàm của hàm số 2 y  x  3 . 2x x 2x  3 1 A. y '  . B. y '  . C. y '  . D. y '  . 2 x  3 2 x  3 2 2 x  3 2 2 x  3 1
Câu 14: Một chất điểm chuyển động theo phương trình 3 2
S   t  6t , trong đó t  0, t được 3
tính bằng giây  s và S tính bằng mét m . Vận tốc của chất điểm tại thời điểm t  2(giây) bằng
A. 22 m / s .
B. 10 m / s .
C. 20 m / s .
D. 6 m / s . 1  5n
Câu 15: lim 3n  bằng 2.5n 1 1 A. 1. B. . C. . D. 0. 3 2
Câu 16: Cho hàm số y  cos 2x . Mệnh đề nào sau đây đúng ?             3 A. y '   3   . B. y '  1    . C. y '  3   . D. y '     .  6   6   6   6  2 3n 1 Câu 17: lim bằng n  6 1 4 A. .  B.  . C. 3. D.  . 6 5 2 x  9 Câu 18: lim x3 x  bằng 3 A. .  B. 3. C. 0. D. 6 Trang 2
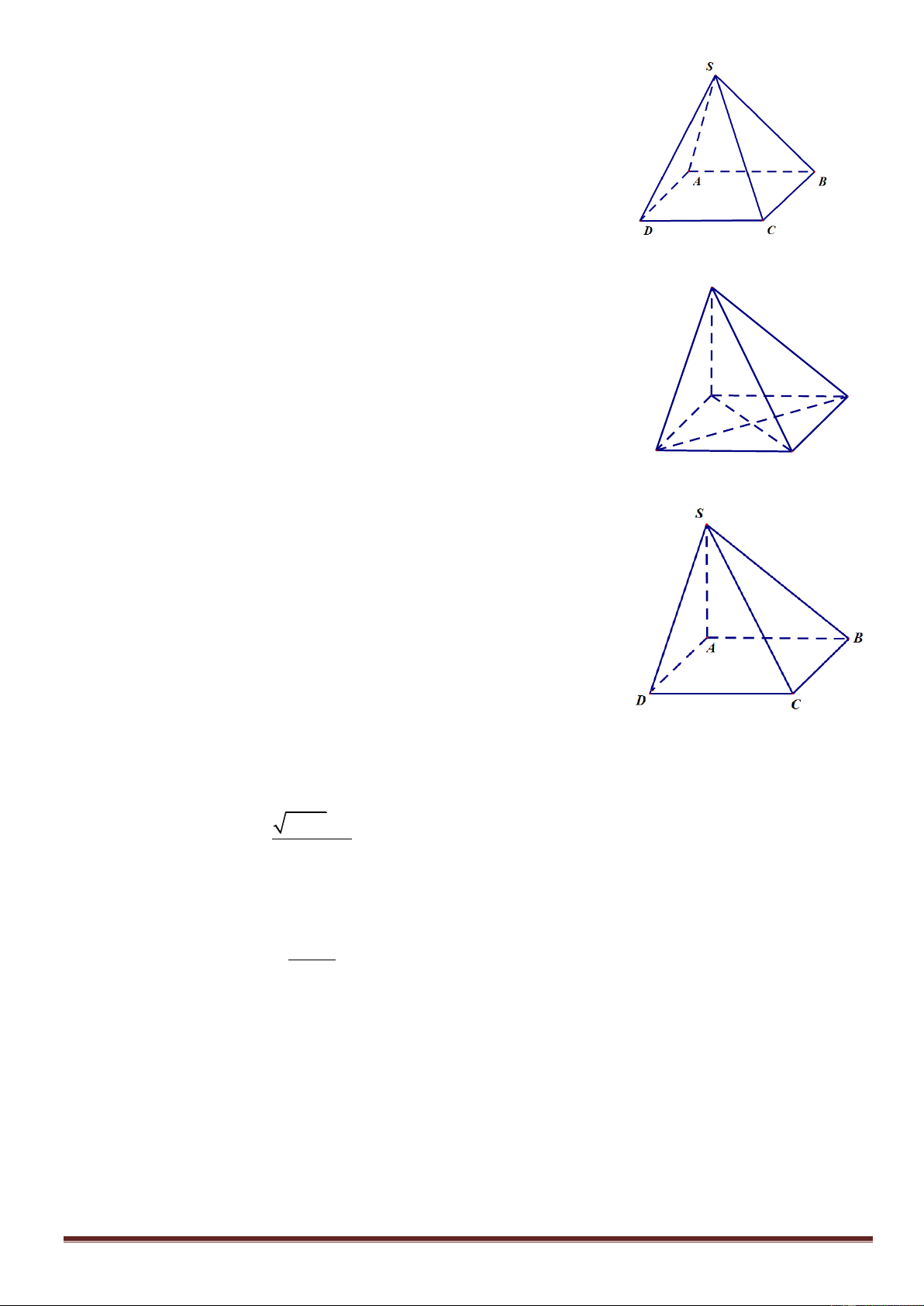
Câu 19: Cho hình chóp S.ABCD có tất cả các cạnh bằng nhau
(hình vẽ minh hoạ). Số đo góc giữa hai đường thẳng SB và AD bằng A. 0 120 . B. 0 30 . C. 0 90 . D. 0 60 . S
Câu 20: Cho hình chóp S.ABCD có đáy là hình thoi, cạnh bên SA
vuông góc với mặt phẳng  ABCD (như hình vẽ minh hoạ). Hãy
chọn khẳng định đúng.
A. BD  (SAC). B. CD  (SA ) D . A B
C. BC  (SAB) .
D. AC  (SB ) D . D C
Câu 21: Cho hình chóp S.ABCD có đáy là hình bình hành (hình
vẽ minh hoạ). Hãy chọn khẳng định đúng.    
A. SA  SD  SB  SC.    
B. SA  AB  SD  DC.    
C. SB  SD  SA  SC.    
D. SA  AD  SB  BC.
B/ TỰ LUẬN: (3,0 điểm)
Bài 1 (2,0 điểm).  x  2 1  khi x  1 
a) Cho hàm số f (x)   x 1
. Tìm tất cả các giá trị của tham số m để hàm số
2x  m khi x  1 
f (x) liên tục tại điểm x  1  . x  b) Cho hàm số 2 1
y  f (x) 
, có đồ thị (C ). Viết phương trình tiếp tuyến của đồ thị C biết x 1
tiếp tuyến vuông góc với đường thẳng d : y  3x  4 .
Bài 2 (1,0 điểm). Cho hình chóp S.ABCD có đáy là hình vuông cạnh a ; SA vuông góc với mặt
phẳng  ABCD và SA  3a. Gọi G là trọng tâm tam giác SAD ,  là góc tạo bởi đường thẳng
CG và mặt phẳng SAC  . Xác định góc  và tính sin.
================= HẾT =================
Họ và tên:……………….......………………….............................SBD: …….......………….
Chú ý: Học sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm. Trang 3 ĐÁP ÁN
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM QUẢNG NAM
ĐỀ KIỂM TRA CUỐI HỌC KỲ II
MÔN: TOÁN 11 – NĂM HỌC 2020-2021
A. Phần trắc nghiệm: (7,0 điểm) Mã Câu
101 102 103 104 105 106 107 108 1 D A B A C C D B 2 D A D A D A D D 3 B C A B C B A A 4 A A B D D A A C 5 C A C A A A A A 6 B C C B A D A A 7 A C C A A C D C 8 A C C B D B B D 9 D B B D A A A C 10 C A B B C A D A 11 C A D A B B B C 12 C C A D D D A A 13 A B A A D C B B 14 D D A C D A D C 15 C A B B C A A C 16 A B A A B A B A 17 C D A D C D D C 18 B D D D C C C D 19 C A C A D D B D 20 C A D A B C D A 21 C B A C D D D C
B. Phần tự luận: (3,0 điểm)
MÃ ĐỀ 102; 104; 106; 108 Câu Nội dung Điểm 1  x  2 1 (2,0 điểm)  khi x  1 
a) Cho hàm số f (x)   x 1
. Tìm tất cả các giá trị của tham số m
2x  m khi x  1 
để hàm số f (x) liên tục tại điểm x  1  . Ta có: f ( 1  )  2
  m và lim f (x)  lim (2x  ) m  2   m .   0,25 x 1  x 1  x  2 1 x 1
lim f (x)  lim  lim    x 1  x 1   x 1 x 1 
(x 1)( x  2 1) 1 1  lim   0,25 x 1  x  2 1 2 Trang 4
Hàm số liên tục tại x  1
 khi và chỉ khi lim f (x)  lim f (x)  f ( 1  )   0,25 x 1  x 1  1 5   2
  m  m  . 0,25 2 2 Vậy 5 m  là giá trị cần tìm. 2 x  b) Cho hàm số 2 1
y  f (x) 
, có đồ thị (C ). Viết phương trình tiếp tuyến của x 1
đồ thị C biết tiếp tuyến vuông góc với đường thẳng d : y  3x  4 .
Tập xác định: D   \   1 .  f  x 3 '   0,25 x  2 1
Gọi M  x ; y  C là tiếp điểm của tiếp tuyến cần tìm  x  1 . 0  0 0    1
Theo giả thuyết, ta có: f 'x   0  0,25 3  x  4   x  2 0 1  9  0 x  2   0
*TH1: x  4  y  3 . 0 0 1 13
Phương trình tiếp tuyến cần tìm là y   x  . 0,25 3 3 *TH2: x  2   y  1. 0 0 1 1
Phương trình tiếp tuyến cần tìm là y   x  . 3 3 0,25 2
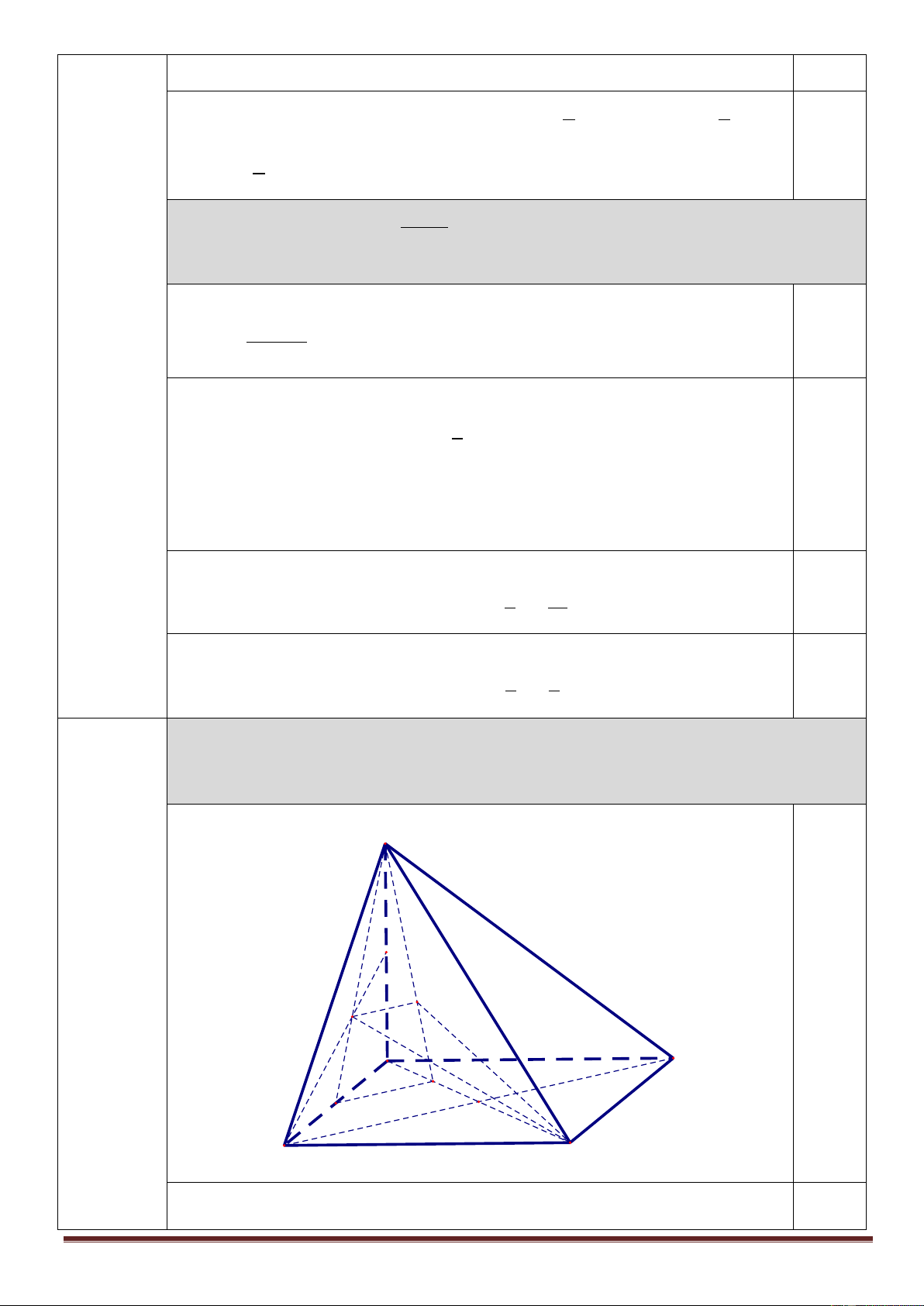
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a ; SA vuông góc với mặt
(1,0 điểm) phẳng  ABCD và SA  3a. Gọi G là trọng tâm tam giác SAD,  là góc tạo bởi
đường thẳng CG và mặt phẳng SAC . Xác định góc  và tính sin . S N H G A B I M O D C
* Gọi O  AC  BD ; M , I , N lần lượt là trung điểm A , D A , O AS . Trang 5 BD  AC 
 BD  SAC  MI  SAC  BD  SA
Kẻ GH / /MI (H  SI )  GH  SAC 0,25  Suy ra CG SAC   ;( )  GCH 2 2 1 a 2 * GH  MI  . BD  0,25 3 3 4 6 2 2 2 2  3a  a 13 2 2 2 DG  DN  DA  AN  a     3 3 3  2  3 C  D  AD 
 CD  SAD  CD  DG C  D  SA 2 13a a 22 2 2 2
 CG  CD  DG  a   9 3 0.25  GH a 2 3 11
sin  sinGCH   .  . GC 6 a 22 22 0,25 Ghi chú:
- Học sinh giải cách khác, giáo viên chia điểm tương tự HDC.
- Tổ Toán mỗi trường cần thảo luận kỹ HDC trước khi tiến hành chấm. Trang 6