
Preview text:
ỦY BAN NHÂN DÂN QUẬN 11 ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2019 - 2020
TRƯỜNG THCS CHU VĂN AN MÔN TOÁN – LỚP 9
Thời gian: 90 phút (không kể thời gian phát đề) ĐỀ CHÍNH THỨC ( Đ ề g ồ m 0 1 t r a n g )
Câu 1: (2 điểm ) Giải phương trình , hệ phương trình 4x y 2 a/ x x 2 3 4 2x 5 b/ x 3y 7
Câu 2:(1,5 điểm) Cho parabol (P) : 2
y x và đường thẳng (D) : y 4x 3
a) Vẽ đồ thị (P) và (D) trên cùng một hệ trục tọa độ Oxy .
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép tính.
Câu 3: (1 điểm) Không giải phương trình 2
3x 15x 6 0, chứng tỏ phương trình có 2 x 1 x 1
nghiệm phân biệt x , x rồi tính giá trị của biểu thức 1 2 A 1 2 x x 2 1
Câu 4: (1 điểm) Cuối năm học, cô Trang mua thước, compa làm phần thưởng tặng học
sinh có tiến bộ trong học tập. Thước giá 3000 đồng/cây, compa giá 6000 đồng/cây. Tổng
số thước và compa là 40 cây và cô Trang đã bỏ ra số tiền là 150000 đồng để mua. Hỏi cô
Trang đã mua bao nhiêu cây mỗi loại ? Câu 5: (1 điểm)
Đường kính của bánh xe đạp là 70cm.
a) Bánh xe quay được bao nhiêu vòng thì xe đi được 8 km?
b) Xe đi được bao nhiêu km nếu bánh xe quay 1000 vòng?
(Kết quả làm tròn đến hàng đơn vị)
Câu 6: (1 điểm) Một hộp sữa Ông Thọ có chiều cao 12cm và đáy là hình
tròn có đường kính 8cm. Tính thể tích hộp sữa.
(Đơn vị cm3; thể tích hình trụ: 2
V R h với R là bán kính đáy, h chiều cao
hình trụ. Kết quả làm tròn 1 chữ số thập phân )
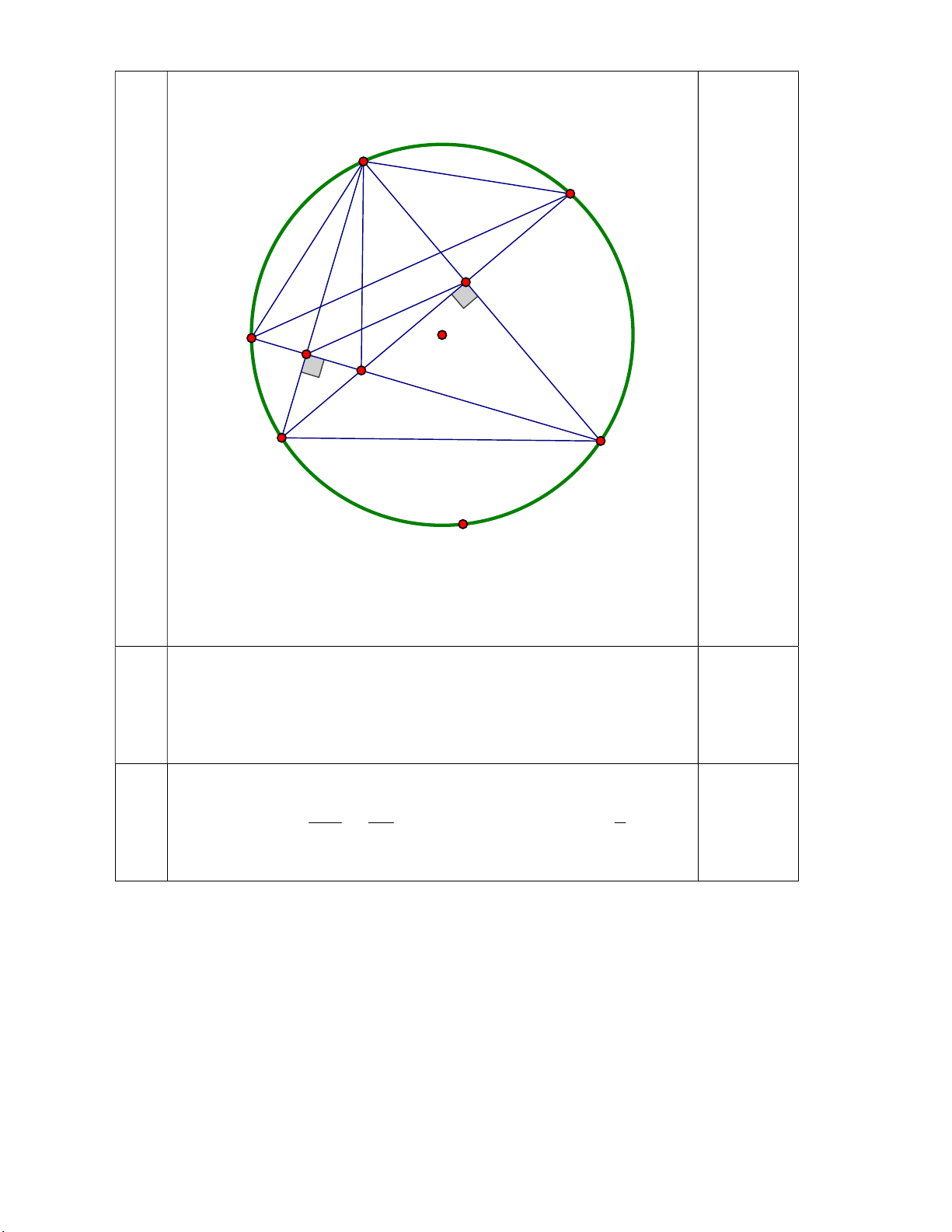
Câu 7: (2,5 điểm) Cho tam giác nhọn ABC nội tiếp (O ; R). Hai đường cao BE, CF cắt nhau tai H.
a) Chứng minh : Tứ giác AEHF nội tiếp.
b) Gọi I và K lần lượt là giao điểm của hai tia BE và CF với (O). Chứng minh : KAI 2 BAC . c) Cho
BAC 60 . Chứng minh : S 3S . BCEF AEF
------------- HẾT ----------- ĐÁP ÁN Câu Điểm x x 2 2 3
4 2x 5 x 4x 5 0 0,25 1a 36 0 0,25
Phương trình có hai nghiệm phân biệt: x 5 ; x 1 0,25 x2 1 2 1b 4x y 2 1 2x 3y 6 1 3x 13 0,25 x2 x 3y 7 x 3y 7 x 3y 7 x 1 0,25 x2 y 2 2a
Bảng giá trị của (P) và (D) đúng 0,25 x2 Vẽ (P) và (D) đúng 0,25 x2 2b
Phương trình hoành độ giao điểm giữa (P) và (D): 2 2
x 4x 3 x 4x 3 0 0,25 x 1 y 1 1 1 x 3 y 9 2 2 0,25
Vậy tọa độ giao điểm của (P) và (D) là ( 1 ; 1 ) , ( 3 ; 9 ) 3 2 3x 15x 6 0
Vì a, c trái dấu ( a = 3 ; c = – 6 ) nên phương trình có 2 nghiệm 0,25 phân biệt x , x 1 2 b S x x 5 1 2
Theo định lý Vi-et ta có: a 0,25 c P x .x 2 1 2 a 2 2 2 x 1 x 1 x x x x S 2P S 1 2 1 2 1 2 A 0,25 x x x x P 2 1 1 2 25 4 5 0,25 1 2 2 4
Đặt ẩn và điều kiện 0,25 x4
Lập phương trình (hoặc hệ phương trình ) đúng
Giải phương trình (hoặc hệ phương trình ) đúng
Vậy : Thước: 30 cây ; compa : 10 cây 5
Số vòng bánh xe quay được khi xe đi được 8 km
800000 : 70 3638 (vòng) 0,5
Số km xe đi được nếu bánh xe quay 1000 vòng 70.1000 :100000 2(km) 0,5 6 Thể tích hộp sữa là: 2 2 3
V R h .4 .12 603(cm ) 0,5x2 7a A I E K F O H B C
a) Chứng minh : Tứ giác AEHF nội tiếp. AEH AFH 9
0 (BE,CF laø caùc ñöôøng cao cuûa ABC) 0,5 AEH AFH 18 0 0,25 0,25 AEFH noäi tieáp. 7b b) Chứng minh : KAI 2 BAC . Cmđ: KAH 2 BAH ; IAH 2 CAH 0,25x2
KAH IAH 2(BAH CAH) 2BAC 0,5 7c c) Chứng minh : S 3S . BCEF AEF S AE 2 AEF 2 AEF ABC BAC 2 1 cos cos60 S AB 0,25 ABC 4 S 4S S S 4S S 3S ABC AEF AEF BCEF AEF BCEF AEF 0,25




