Đề thi HKII năm 2020-2021 môn toán Sở GD Quảng Nam Mã đề A (có lời giải)

Tổng hợp Đề thi HKII năm 2020-2021 môn toán Sở GD Quảng Nam Mã đề A (có lời giải) rất hay và bổ ích giúp bạn đạt điểm cao. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc đón xem.

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 9

Môn: Toán 9

Thông tin:

8 trang 9 tháng trước

Tác giả:

Profile Minh Thư
Trang 1
ĐỀ CHÍNH THỨC
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
(Đề gồm có 02 trang)
KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2020-2021
Môn: TOÁN – Lớp 9
Thời gian: 60 phút (không kể thời gian giao đề)
MÃ ĐỀ A
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm)
(Chọn chữ cái trước ý trả lời đúng nhất trong các câu sau và ghi vào giấy làm bài)
Câu 1. Hệ phương trình

2x 3y 1
x y 2
có nghiệm (x; y) là
A. (
1; 1).
C. (1;
1).
D. (
1;
1).
Câu 2. Đồ thị hàm số y = 4x
2
đi qua điểm nào sau đây ?
A. M(
1;
4).
C. P(
2; 16).
D. Q(
2;
16).
Câu 3. Hàm số y = x
2
đồng biến khi
A. x ≠ 0.
C. x > 0.
D. x < 0.
Câu 4. Biệt thức
(đenta) của phương trình 2x
2
x
2 = 0 bằng
A. 15.
C.
17.
D.
15.
Câu 5. Phương trình
2
0ax bx c
(
a
0) có ∆ = 0 thì phương trình có nghiệm kép là
A.
12
2
b
xx
a
B.
12
b
xx
a
C.
12
c
xx
a
D.
12
2
c
xx
a
Câu 6. Với điều kiện nào sau đây thì phương trình
2
0ax bx c
(
a
0) vô nghiệm ?
A.
2
4 0.b ac
2
0.b ac
C.
2
4 0.b ac
D.
2
4 0.b ac
Câu 7. Phương trình x
2
– 2x – 6 = 0 có tổng của hai nghiệm bằng
B. 2.
C. 6.
D.
6.
Câu 8. Phương trình
a
x
2
+ bx + c = 0 (a ≠ 0) có
a
– b + c = 0 thì phương trình có hai nghiệm là
b
a
B. –1;
b
a
C. –1;
c
a
D. 1;
c
a
Câu 9. Số đo của nửa đường tròn bằng
A. 90
0
.
C. 180
0
.
D. 360
0
.
Câu 10. Trên đường tròn tâm O lấy hai điểm A, B sao cho sđ
AB
= 60
0
thì
·
AOB
bằng
A. 30
0
.
C. 90
0
.
D. 180
0
.
Câu 11. Cho đường tròn (O), dây AB cắt dây CD tại E (Hình 1), ta có
BEC
bằng
A. (sđ
BnC
+ sđ
BpD
) : 2.
B. (sđ
BnC
sđ
AmD
) : 2.
C. (sđ
BnC
sđ
AqC
) : 2.
D. (sđ
AmD
+ sđ
BnC
) : 2.
Câu 12. Trên Hình 1, ta có
BCD
bằng Hình 1
A. (sđ
BpD
) : 2.
B. (sđ
AqC
) : 2.
C. (sđ
BnC
) : 2.
D. (sđ
AmD
) : 2.
Câu 13. Cho tứ giác DEHF nội tiếp đường tròn (O) có
0
65EHF
. Khi đó ta có
A.
0
115 .EDF
0
115 .DEH
C.
0
115 .DFH
D.
0
65 .EDF
Câu 14. Độ dài đường tròn (O; 4cm) bằng
A. 16π cm.
C. 4π cm.
D. 2π cm.
Câu 15. Độ dài cung có số đo 60
0
của một đường tròn có bán kính 9 cm bằng
A. 6π cm.
C. 2π cm.
D. 3π cm.
PHẦN II. TỰ LUẬN (5,0 điểm)
m
n
q
p
E
O
A
D
C
B
Trang 2
Bài 1. (1,5 điểm)
a) Giải hệ phương trình
5
27
.
xy
xy


b) Giải phương trình
2
2 5 2 0xx
.
Bài 2. (1,25 điểm)
a) Vẽ đồ thị hàm số
2
2 .yx
b) Cho phương trình bậc hai ẩn x:
22
4 4 2 0x mx m
(m là tham số).
Tìm m để phương trình có hai nghiệm
12
,xx
thỏa mãn hệ thức
22
12
4 4 6 0.x mx m
Bài 3. (2,25 điểm)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD và BE của
tam giác cắt nhau tại H ( D
BC, E
AC).
a) Chứng minh tứ giác CDHE nội tiếp đường tròn.
b) Tia BE cắt đường tròn (O) tại F (F khác B). Chứng minh
·
·
AHF AFH.=
c) Gọi M là trung điểm của AB. Chứng minh ME là tiếp tuyến của đường tròn ngoại tiếp
tam giác CDE.
-----------Hết----------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ II
NĂM HỌC 2020-2021
Môn: TOÁN – LỚP 9
MÃ ĐỀ A
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm)
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Đ/án
C
C
C
B
A
D
B
C
C
B
D
A
A
B
D
(Mỗi câu TNKQ đúng được 1/3 điểm.)
PHẦN II. TỰ LUẬN (5,0 điểm)
Hướng dẫn chấm
Điểm
Bài 1
(1,5 )
a) 0,75
a) Giải hệ phương trình:
5
27
xy
xy


Cách 1:
5 3 12
2 7 5
x y x
x y x y



0,25
4
45
x
y

0,25
4
1
x
y

Kết luận: Nghiệm của hệ phương trình là (4;-1)
0,25
Trang 3
Cách 2:
55
2 7 2 7
x y x y
x y x y



0,25
5
2.(5 ) 7
xy
yy

5
33
xy
y


0,25
4
1
x
y

Kết luận: Nghiệm của hệ phương trình là (4;-1)
0,25
b) 0,75
b) Giải phương trình :
2
2 5 2 0xx
.
2
( 5) 4.2.2
9
0,25
0,1
Tính đúng
12
1
2;
2
xx
.
0,4
Bài 2
(1,25)
a) 0,75
a) Vẽ đồ thị hàm số:
2
2yx
.
Lập được bảng biến thiên, ít nhất có 5 giá trị đảm bảo tính chất đối
xứng
0,25
Vẽ đúng
0,5
Nếu bảng biến thiên sai hoặc không có thì không cho điểm hình
vẽ đồ thị
b) 0,5
b) Cho phương trình bậc hai ẩn x:
22
4 4 2 0x mx m
(m là tham số)
Tìm m để phương trình có hai nghiệm x
1
, x
2
thỏa mãn hệ thức
22
12
4 4 6 0x mx m
Tính đúng
8
hoặc
'2
. Suy ra phương trình đã cho có
nghiệm với mọi m.
0,1
Áp dụng hệ thức Viet ta có
12
4x x m
0,1
22
12
4 4 6 0x mx m
22
1 1 1 2
( 4 4 2) 4 ( ) 4 0x mx m m x x
0 4 .4 4 0mm
0,1
2
16 4m
0,1
1
2
m
0,1
Bài 3
(2,25)
Hình vẽ đủ và đúng để phục vụ các câu a, b
0,25
Trang 4
ĐỀ CHÍNH THỨC
a) 0,75
a) Chứng minh tứ giác CDHE nội tiếp đường tròn.
Nêu được
·
·
0
HDC HEC 90 .==
0,25
·
·
0
HDC HEC 180 .Þ + =
0,25
Kết luận tứ giác CDHE nội tiếp
0,25
b) 0,75
b) Tia BE cắt đường tròn (O) tại F (F khác B). Chứng minh
·
·
AHF AFH.=
Nêu được
· ·
AH F DCE=
(vì tứ giác CDHE nội tiếp)
0,25
Và
·
·
DCE AFH=
(góc nội tiếp cùng chắn cung AB)
0,25
Suy ra
·
·
AHF AFH.=
0,25
c) 0,5
c)
Gọi M là trung điểm của AB. Chứng minh ME là tiếp tuyến
của đường tròn ngoại tiếp tam giác CDE.
Chỉ ra được tâm đường tròn ngoại tiếp tam giác CDE là trung điểm
I của đoạn thẳng HC
0,1
Chứng minh được
·
·
MEA MAE=
và
·
·
IEC ICE=
0,1
mà
·
·
0
MAE ICE 90+=
(do H là trực tâm của tam giác ABC).
0,1
·
·
·
00
MEA IEC 90 MEI 90Þ + = Þ =
0,1
Kết luận ME là tiếp tuyến của đường tròn ngoại tiếp tam giác CDE
0,1
Tất cả các cách giải khác của học sinh nếu đúng thì người chấm cho điểm tương ứng với
hướng dẫn này.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2020-2021
Môn: TOÁN – Lớp 9
Thời gian: 60 phút (không kể thời gian giao đề)
Trang 5
(Đề gồm có 02 trang)
MÃ ĐỀ B
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm)
(Chọn chữ cái trước ý trả lời đúng nhất trong các câu sau và ghi vào giấy làm bài)
Câu 1. Hệ phương trình

2x 3y 1
x y 2
có nghiệm (x; y) là
A. (
1; 1).
C. (1;
1).
D. (
1;
1).
Câu 2. Đồ thị hàm số y = 3x
2
đi qua điểm nào sau đây ?
A. M(
1;
3).
C. P(
2;
12).
D. Q(
2; 12).
Câu 3. Hàm số y = x
2
nghịch biến khi
A. x ≠ 0.
C. x > 0.
D. x < 0.
Câu 4. Biệt thức
(đenta) của phương trình 2x
2
x
3 = 0 bằng
A. 25.
C.
25.
D.
23.
Câu 5. Phương trình
2
0ax bx c
(
a
0) có ∆ = 0 thì phương trình có nghiệm kép là
A.
12
b
xx
a
B.
12
2
b
xx
a
C.
12
c
xx
a
D.
12
2
c
xx
a
Câu 6. Với điều kiện nào sau đây thì phương trình
2
0ax bx c
(
a
0) có hai nghiệm phân
biệt?
A.
2
4 0.b ac
2
0.b ac
C.
2
4 0.b ac
D.
2
4 0.b ac
Câu 7. Phương trình x
2
– 2x – 6 = 0 có tích của hai nghiệm bằng
B. 2.
C. 6.
D.
6.
Câu 8. Phương trình
a
x
2
+ bx + c = 0 (a ≠ 0) có
a
+ b + c = 0 thì phương trình có hai nghiệm là
b
a
B. 1;
b
a
C. 1;
c
a
D. 1;
c
a
Câu 9. Số đo của nửa đường tròn bằng
A. 360
0
.
C. 120
0
.
D. 90
0
.
Câu 10. Trên đường tròn tâm O lấy hai điểm A, B sao cho sđ
AB
= 90
0
thì
AOB
bằng
A. 90
0
.
C. 180
0
.
D. 360
0
.
Câu 11. Cho đường tròn (O), dây AB cắt dây CD tại E (Hình 1), ta có
BED
bằng
A. (sđ
BpD
+ sđ
AmD
) : 2.
B. (sđ
BpD
sđ
AqC
) : 2.
C. (sđ
BpD
+ sđ
AqC
) : 2.
D. (sđ
AmD
+ sđ
BnC
) : 2.
Câu 12. Trên Hình 1, ta có
ABC
bằng Hình 1
A. (sđ
BnC
) : 2.
B. (sđ
AqC
) : 2.
C. (sđ
BpD
) : 2.
D. (sđ
AmD
) : 2.
Câu 13. Cho tứ giác DEHF nội tiếp đường tròn (O), có
0
65DFH
. Khi đó ta có
A.
0
115 .EHF
0
115 .DEH
C.
0
65 .DEH
D.
0
115 .EDF
Câu 14. Độ dài đường tròn (O; 6cm) bằng
A. 24π cm.
C. 12π cm.
D. 6π cm.
Câu 15. Độ dài cung có số đo 45
0
của một đường tròn có bán kính 8 cm bằng
A. 4π cm.
C. 2π cm.
D. π cm.
PHẦN II. TỰ LUẬN (5,0 điểm)
Bài 1. (1,5 điểm)
m
n
q
p
E
O
A
D
C
B
Trang 6
a) Giải hệ phương trình
4
2 11
.
xy
xy


b) Giải phương trình
2
2 7 3 0xx
.
Bài 2. (1,25 điểm)
a) Vẽ đồ thị hàm số
2
.yx
b) Cho phương trình bậc hai ẩn x:
22
6 9 3 0x mx m
(m là tham số)
Tìm m để phương trình có hai nghiệm
12
,xx
thỏa mãn hệ thức
22
12
6 9 7 0.x mx m
Bài 3. (2,25 điểm)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao BD và CE của
tam giác cắt nhau tại K ( D
AC, E
AB).
a) Chứng minh tứ giác ADKE nội tiếp đường tròn.
b) Tia BD cắt đường tròn (O) tại I (I khác B). Chứng minh
·
·
CIK CKI.=
c) Gọi N là trung điểm của BC. Chứng minh ND là tiếp tuyến của đường tròn ngoại tiếp tam
giác ADE.
----------Hết----------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NAM
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ II
NĂM HỌC 2020-2021
Môn: TOÁN – LỚP 9
MÃ ĐỀ B
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm)
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Đ/án
A
D
D
A
B
C
D
D
B
A
C
B
B
C
C
(Mỗi câu TNKQ đúng được 1/3 điểm)
PHẦN II. TỰ LUẬN (5,0 điểm)
Hướng dẫn chấm
Điểm
Bài 1
(1,5 )
a) 0,75
a) Giải hệ phương trình:
4
2 11
xy
xy


Cách 1:
4 3 15
2 11 4
x y x
x y x y



0,25
5
54
x
y

0,25
5
1
x
y
Kết luận: Nghiệm của hệ phương trình là (5;1)
0,25
Trang 7
Cách 2:
44
2 11 2 11
x y x y
x y x y



0,25
4
2.(4 ) 11
xy
yy

4
33
xy
y

0,25
5
1
x
y
Kết luận: Nghiệm của hệ phương trình là (5;1)
0,25
b) 0,75
b) Giải phương trình :
2
2 7 3 0xx
.
2
( 7) 4.2.3
25
0,25
0,1
Tính đúng
12
1
3;
2
xx
.
0,4
Bài 2
(1,25)
a) 0,75
a) Vẽ đồ thị hàm số:
2
yx
.
Lập được bảng biến thiên, ít nhất có 5 giá trị đảm bảo tính chất đối
xứng
0,25
Vẽ đúng
0,5
Nếu bảng biến thiên sai hoặc không có thì không cho điểm hình
vẽ đồ thị
b) 0,5
b) Cho phương trình bậc hai ẩn x:
22
6 9 3 0x mx m
(m là tham số)
Tìm m để phương trình có hai nghiệm x
1
,x
2
thỏa mãn hệ thức
22
12
6 9 7 0x mx m
Tính đúng
12
hoặc
'3
. Suy ra phương trình đã cho có
nghiệm với mọi m.
0,1
Áp dụng hệ thức Viet ta có
12
6x x m
0,1
22
12
6 9 7 0x mx m
22
1 1 1 2
( 6 9 3) 6 ( ) 4 0x mx m m x x
0 6 .6 4 0mm
0,1
2
36 4m
0,1
1
3
m
0,1
Bài 3
(2,25)
Hình vẽ đủ và đúng để phục vụ các câu a, b
0,25
Trang 8
a) 0,75
a) Chứng minh tứ giác ADKE nội tiếp đường tròn.
Nêu được
·
·
0
ADK AEK 90 .==
0,25
·
·
0
ADK AEK 180 .Þ + =
0,25
Kết luận tứ giác ADKE nội tiếp
0,25
b) 0,75
b) Tia BD cắt đường tròn (O) tại I (I khác B). Chứng minh
·
·
CIK CKI.=
Nêu được
·
·
EAD CKI=
(vì tứ giác ADKE nội tiếp)
0,25
Và
·
·
CIK EAD=
(góc nội tiếp cùng chắn cung BC)
0,25
Suy ra
·
·
CIK CKI.=
0,25
c) 0,5
c)
Gọi N là trung điểm của BC. Chứng minh ND là tiếp tuyến
của đường tròn ngoại tiếp tam giác ADE.
Chỉ ra được tâm đường tròn ngoại tiếp tam giác ADE là trung
điểm J của đoạn thẳng AK
0,1
Chứng minh được
·
·
JDA J DA=
và
· ·
NDC NCD.=
0,1
mà
·
·
0
JAD NCD 90+=
(do K là trực tâm của tam giác ABC).
0,1
·
·
·
00
JDA ND 90 NDJ 90CÞ + = Þ =
0,1
Kết luận ND là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE
0,1
Tất cả các cách giải khác của học sinh nếu đúng thì người chấm cho điểm tương ứng với
hướng dẫn này
| 1/8
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2020-2021 QUẢNG NAM
Môn: TOÁN – Lớp 9
Thời gian: 60 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
(Đề gồm có 02 trang) MÃ ĐỀ A
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm)
(Chọn chữ cái trước ý trả lời đúng nhất trong các câu sau và ghi vào giấy làm bài) 2x  3y  1
Câu 1. Hệ phương trình  có nghiệm (x; y) là x  y  2 A. (  1; 1). B. (1; 1). C. (1;  1). D. (  1;  1).
Câu 2. Đồ thị hàm số y = 4x2 đi qua điểm nào sau đây ? A. M(  1;  4). B. N(  2; 8). C. P(  2; 16). D. Q(  2;  16).
Câu 3. Hàm số y = x2 đồng biến khi A. x ≠ 0. B. x ≤ 0. C. x > 0. D. x < 0.
Câu 4. Biệt thức  (đenta) của phương trình 2x2  x  2 = 0 bằng A. 15. B. 17. C.  17. D.  15.
Câu 5. Phương trình 2
ax bx c  0 ( a  0) có ∆ = 0 thì phương trình có nghiệm kép là bbcc A. x x   B. x x   C. x x   D. x x   1 2 2a 1 2 a 1 2 a 1 2 2a
Câu 6. Với điều kiện nào sau đây thì phương trình 2
ax bx c  0 ( a  0) vô nghiệm ? A. 2
b  4ac  0. B. 2 b ac  0. C. 2
b  4ac  0. D. 2
b  4ac  0.
Câu 7. Phương trình x2 – 2x – 6 = 0 có tổng của hai nghiệm bằng A. –2. B. 2. C. 6. D.  6.
Câu 8. Phương trình a x2 + bx + c = 0 (a ≠ 0) có a – b + c = 0 thì phương trình có hai nghiệm là bbcc A. 1;  B. –1;  C. –1;  D. 1;  a a a a
Câu 9. Số đo của nửa đường tròn bằng A. 900. B. 1200. C. 1800. D. 3600. ·
Câu 10. Trên đường tròn tâm O lấy hai điểm A, B sao cho sđ AB = 600 thì AOB bằng A. 300. B. 600. C. 900. D. 1800.
Câu 11. Cho đường tròn (O), dây AB cắt dây CD tại E (Hình 1), ta có BEC bằng
A. (sđ BnC + sđ BpD ) : 2.
B. (sđ BnC  sđ AmD ) : 2. m A D
C. (sđ BnC  sđ AqC ) : 2. D. (sđ AmD + sđ BnC ) : 2. E q p
Câu 12. Trên Hình 1, ta có BCD bằng O Hình 1 C A. (sđ BpD ) : 2. B. (sđ AqC ) : 2. n B C. (sđ BnC ) : 2. D. (sđ AmD ) : 2.
Câu 13. Cho tứ giác DEHF nội tiếp đường tròn (O) có EHF  0 65 . Khi đó ta có A. EDF  0 115 . B. DEH  0 115 . C. DFH  0 115 . D. E DF  0 65 .
Câu 14. Độ dài đường tròn (O; 4cm) bằng A. 16π cm. B. 8π cm. C. 4π cm. D. 2π cm.
Câu 15. Độ dài cung có số đo 600 của một đường tròn có bán kính 9 cm bằng A. 6π cm. B. π cm. C. 2π cm. D. 3π cm.
PHẦN II. TỰ LUẬN (5,0 điểm) Trang 1 Bài 1. (1,5 điểm) x y  5
a) Giải hệ phương trình  . 2x y  7  b) Giải phương trình 2
2x  5x  2  0 . Bài 2. (1,25 điểm) a) Vẽ đồ thị hàm số 2
y  2x .
b) Cho phương trình bậc hai ẩn x: 2 2
x  4mx  4m  2  0 (m là tham số).
Tìm m để phương trình có hai nghiệm x , x thỏa mãn hệ thức 1 2 2 2
x  4mx  4m  6  0. 1 2 Bài 3. (2,25 điểm)
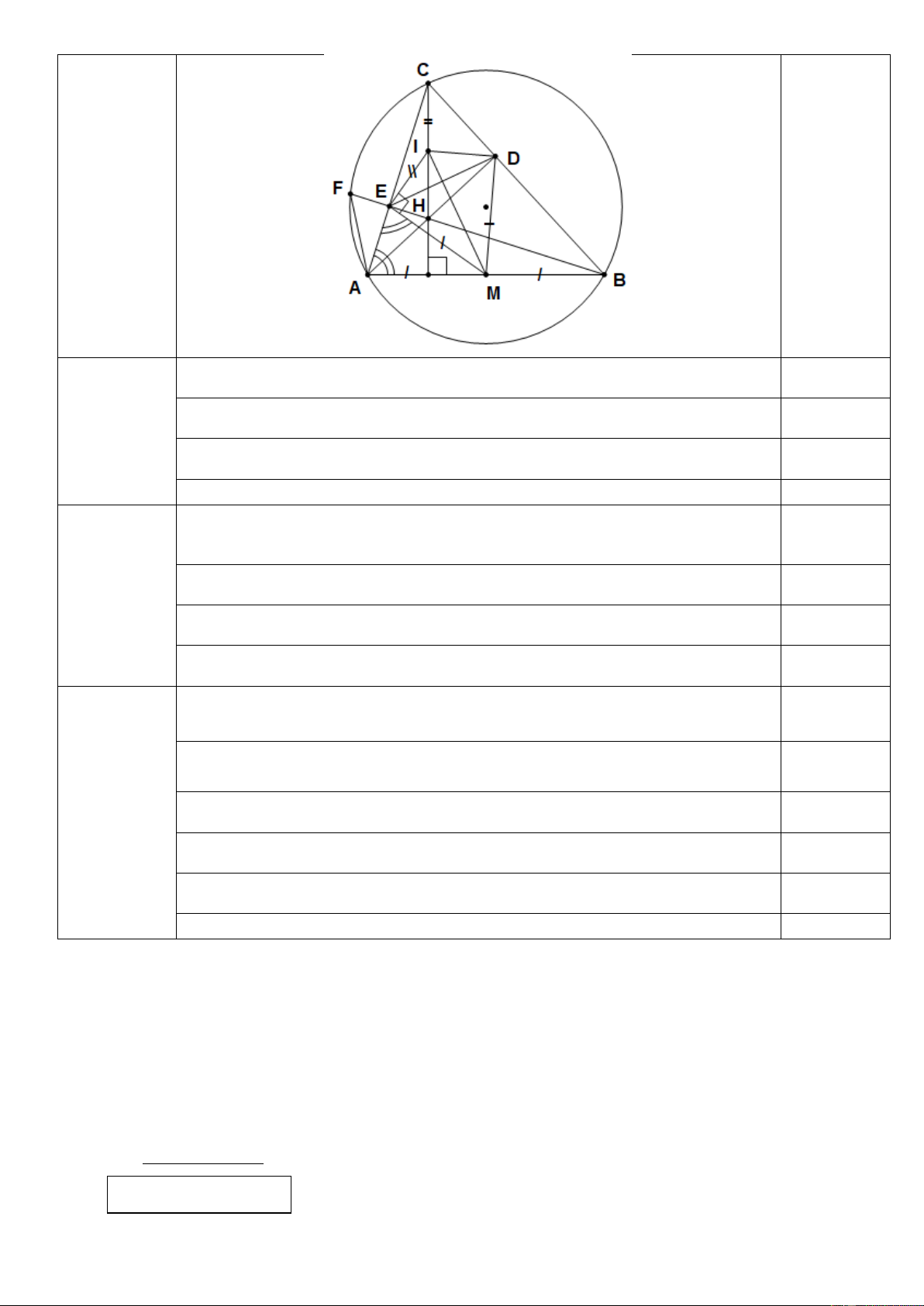
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD và BE của
tam giác cắt nhau tại H ( DBC, EAC).
a) Chứng minh tứ giác CDHE nội tiếp đường tròn. · ·
b) Tia BE cắt đường tròn (O) tại F (F khác B). Chứng minh AHF = AFH.
c) Gọi M là trung điểm của AB. Chứng minh ME là tiếp tuyến của đường tròn ngoại tiếp tam giác CDE. -----------Hết----------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ II NĂM HỌC 2020-2021 QUẢNG NAM
Môn: TOÁN – LỚP 9 MÃ ĐỀ A
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Đ/án C C C B A D B C C B D A A B D
(Mỗi câu TNKQ đúng được 1/3 điểm.)
PHẦN II. TỰ LUẬN (5,0 điểm) Hướng dẫn chấm Điểm Bài 1 (1,5 ) x y
a) Giải hệ phương trình: 5 
2x y  7 Cách 1: x y  5 3  x 12 0,25   
2x y  7 x y  5 x  4   0,25    4 y 5 a) 0,75 x  4  y  1 0,25
Kết luận: Nghiệm của hệ phương trình là (4;-1) Trang 2 Cách 2: x y  5 x  5  y 0,25   
2x y  7
2x y  7 x  5  y     x 5 y    0,25
2.(5  y)  y  7 3  y  3 x  4  y  1 0,25
Kết luận: Nghiệm của hệ phương trình là (4;-1) b) 0,75
b) Giải phương trình : 2
2x  5x  2  0 . 2   ( 5  )  4.2.2 0,25   9 0,1 Tính đúng 1
x  2; x . 1 2 2 0,4 Bài 2 (1,25)
a) Vẽ đồ thị hàm số: 2
y  2x .
Lập được bảng biến thiên, ít nhất có 5 giá trị đảm bảo tính chất đối 0,25 a) 0,75 xứng Vẽ đúng 0,5
Nếu bảng biến thiên sai hoặc không có thì không cho điểm hình
vẽ đồ thị
b) Cho phương trình bậc hai ẩn x: 2 2
x  4mx  4m  2  0
(m là tham số)
Tìm m để phương trình có hai nghiệm x1 , x2 thỏa mãn hệ thức 2 2
x  4mx  4m  6  0 1 2
Tính đúng   8 hoặc '  2 . Suy ra phương trình đã cho có 0,1 nghiệm với mọi m. Áp dụng hệ thứ
c Viet ta có x x  4m 0,1 1 2 b) 0,5 2 2
x  4mx  4m  6  0 1 2 2 2
 (x  4mx  4m  2)  4 (
m x x )  4  0 1 1 1 2 0,1  0 4 . m 4m  4  0 2  16m  4 0,1 1  m   2 0,1 Bài 3 (2,25)
Hình vẽ đủ và đúng để phục vụ các câu a, b 0,25 Trang 3
a) Chứng minh tứ giác CDHE nội tiếp đường tròn. Nêu được · · 0 HDC = HEC = 90 . 0,25 a) 0,75 · · 0 Þ HDC+ HEC = 180 . 0,25
Kết luận tứ giác CDHE nội tiếp 0,25
b) Tia BE cắt đường tròn (O) tại F (F khác B). Chứng minh · · AHF = AFH. Nêu được · ·
AHF = DCE (vì tứ giác CDHE nội tiếp) b) 0,75 0,25 Và · ·
DCE = AFH (góc nội tiếp cùng chắn cung AB) 0,25 Suy ra · · AHF = AFH. 0,25
c) Gọi M là trung điểm của AB. Chứng minh ME là tiếp tuyến
của đường tròn ngoại tiếp tam giác CDE.
Chỉ ra được tâm đường tròn ngoại tiếp tam giác CDE là trung điểm 0,1 I của đoạn thẳng HC
Chứng minh được · · MEA = MAE và · · IEC = ICE 0,1 c) 0,5 mà · · 0
MAE+ ICE = 90 (do H là trực tâm của tam giác ABC). 0,1 · · 0 · 0 Þ MEA + IEC= 90 Þ MEI = 90 0,1
Kết luận ME là tiếp tuyến của đường tròn ngoại tiếp tam giác CDE 0,1
Tất cả các cách giải khác của học sinh nếu đúng thì người chấm cho điểm tương ứng với
hướng dẫn này.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2020-2021 QUẢNG NAM
Môn: TOÁN – Lớp 9 ĐỀ CHÍNH THỨC
Thời gian: 60 phút (không kể thời gian giao đề) Trang 4
(Đề gồm có 02 trang) MÃ ĐỀ B
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm)
(Chọn chữ cái trước ý trả lời đúng nhất trong các câu sau và ghi vào giấy làm bài) 2x  3y 1
Câu 1. Hệ phương trình  có nghiệm (x; y) là x  y  2 A. (  1; 1). B. (1; 1). C. (1;  1). D. (  1;  1).
Câu 2. Đồ thị hàm số y = 3x2 đi qua điểm nào sau đây ? A. M(  1;  3). B. N(  2; 6). C. P(  2;  12). D. Q(  2; 12).
Câu 3. Hàm số y = x2 nghịch biến khi A. x ≠ 0. B. x ≥ 0. C. x > 0. D. x < 0.
Câu 4. Biệt thức  (đenta) của phương trình 2x2  x  3 = 0 bằng A. 25. B. 23. C.  25. D.  23.
Câu 5. Phương trình 2
ax bx c  0 ( a  0) có ∆ = 0 thì phương trình có nghiệm kép là bbcc A. x x   B. x x   C. x x   D. x x   1 2 a 1 2 2a 1 2 a 1 2 2a
Câu 6. Với điều kiện nào sau đây thì phương trình 2
ax bx c  0 ( a  0) có hai nghiệm phân biệt? A. 2
b  4ac  0. B. 2 b ac  0. C. 2
b  4ac  0. D. 2
b  4ac  0.
Câu 7. Phương trình x2 – 2x – 6 = 0 có tích của hai nghiệm bằng A. –2. B. 2. C. 6. D.  6.
Câu 8. Phương trình a x2 + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có hai nghiệm là bbc c A. 1;  B. 1;  C. 1;  D. 1;  a a a a
Câu 9. Số đo của nửa đường tròn bằng A. 3600 . B. 1800 . C. 1200 . D. 900.
Câu 10. Trên đường tròn tâm O lấy hai điểm A, B sao cho sđ AB = 900 thì AOB bằng A. 900 . B. 450 . C. 1800 . D. 3600.
Câu 11. Cho đường tròn (O), dây AB cắt dây CD tại E (Hình 1), ta có BED bằng
A. (sđ BpD + sđ AmD ) : 2.
B. (sđ BpD  sđ AqC ) : 2. m A D
C. (sđ BpD + sđ AqC ) : 2.
D. (sđ AmD + sđ BnC ) : 2. E q p
Câu 12. Trên Hình 1, ta có ABC bằng O Hình 1 C A. (sđ BnC ) : 2. B. (sđ AqC ) : 2. n B C. (sđ BpD ) : 2. D. (sđ AmD ) : 2.
Câu 13. Cho tứ giác DEHF nội tiếp đường tròn (O), có 0
DFH  65 . Khi đó ta có A. 0 EHF  115 . B. 0 DEH  115 . C. 0 DEH  65 . D. E 0 DF  115 .
Câu 14. Độ dài đường tròn (O; 6cm) bằng A. 24π cm. B. 16π cm. C. 12π cm. D. 6π cm.
Câu 15. Độ dài cung có số đo 450 của một đường tròn có bán kính 8 cm bằng A. 4π cm. B. 3π cm. C. 2π cm. D. π cm.
PHẦN II. TỰ LUẬN (5,0 điểm) Bài 1. (1,5 điểm) Trang 5x y  4
a) Giải hệ phương trình  . 2x y  11  b) Giải phương trình 2
2x  7x  3  0 . Bài 2. (1,25 điểm) a) Vẽ đồ thị hàm số 2
y x .
b) Cho phương trình bậc hai ẩn x: 2 2
x  6mx  9m  3  0 (m là tham số)
Tìm m để phương trình có hai nghiệm x , x thỏa mãn hệ thức 1 2 2 2
x  6mx  9m  7  0. 1 2 Bài 3. (2,25 điểm)
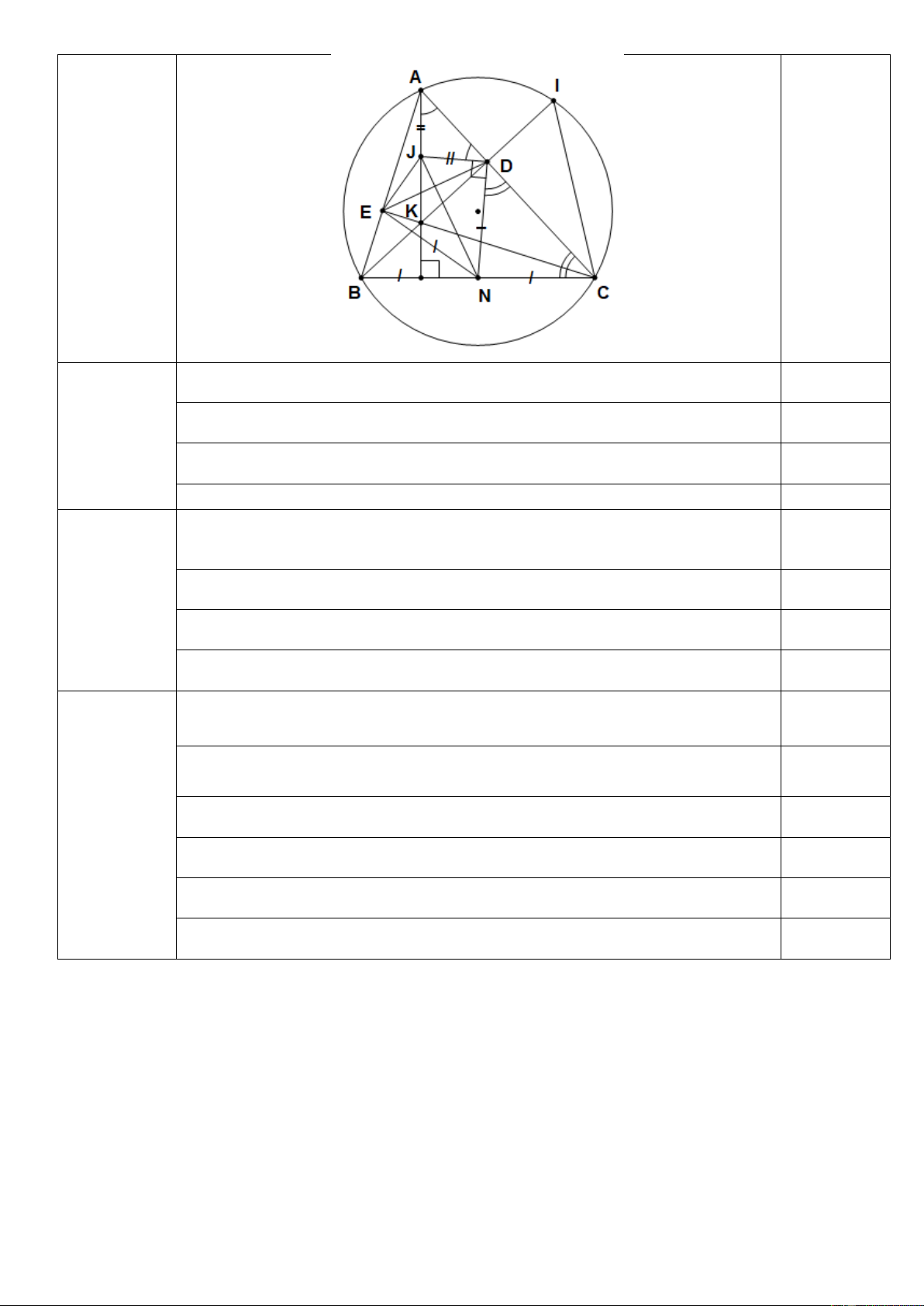
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao BD và CE của
tam giác cắt nhau tại K ( D  AC, E  AB).
a) Chứng minh tứ giác ADKE nội tiếp đường tròn.
b) Tia BD cắt đường tròn (O) tại I (I khác B). Chứng minh · · CIK = CKI.
c) Gọi N là trung điểm của BC. Chứng minh ND là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE. ----------Hết----------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ II NĂM HỌC 2020-2021 QUẢNG NAM
Môn: TOÁN – LỚP 9 MÃ ĐỀ B
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Đ/án A D D A B C D D B A C B B C C
(Mỗi câu TNKQ đúng được 1/3 điểm)
PHẦN II. TỰ LUẬN (5,0 điểm) Hướng dẫn chấm Điểm Bài 1 (1,5 ) x y
a) Giải hệ phương trình: 4 
2x y  11 Cách 1: x y  4 3  x 15 0,25   
2x y 11 x y  4 x  5   0,25    5 y 4 a) 0,75 x  5  y 1 0,25
Kết luận: Nghiệm của hệ phương trình là (5;1) Trang 6 Cách 2: x y  4 x  4  y 0,25   
2x y 11
2x y 11 x  4  y     x 4 y    0,25
2.(4  y)  y 11 3  y  3 x  5  y 1 0,25
Kết luận: Nghiệm của hệ phương trình là (5;1) b) 0,75
b) Giải phương trình : 2
2x  7x  3  0 . 2   ( 7  )  4.2.3 0,25   25 0,1 Tính đúng 1
x  3; x . 0,4 1 2 2 Bài 2 (1,25)
a) Vẽ đồ thị hàm số: 2
y x .
Lập được bảng biến thiên, ít nhất có 5 giá trị đảm bảo tính chất đối 0,25 a) 0,75 xứng Vẽ đúng 0,5
Nếu bảng biến thiên sai hoặc không có thì không cho điểm hình
vẽ đồ thị
b) Cho phương trình bậc hai ẩn x: 2 2
x  6mx  9m  3  0
(m là tham số)
Tìm m để phương trình có hai nghiệm x1 ,x2 thỏa mãn hệ thức 2 2
x  6mx  9m  7  0 1 2
Tính đúng  12 hoặc '  3. Suy ra phương trình đã cho có 0,1 nghiệm với mọi m. Áp dụng hệ thứ
c Viet ta có x x  6m 1 2 0,1 b) 0,5 2 2
x  6mx  9m  7  0 1 2 2 2
 (x 6mx 9m 3)  6 (
m x x )  4  0 1 1 1 2 0,1  0 6 . m 6m  4  0 2  36m  4 0,1 1  m   3 0,1 Bài 3 (2,25)
Hình vẽ đủ và đúng để phục vụ các câu a, b 0,25 Trang 7
a) Chứng minh tứ giác ADKE nội tiếp đường tròn. Nêu được · · 0 ADK = AEK = 90 . 0,25 a) 0,75 · · 0 Þ ADK + AEK = 180 . 0,25
Kết luận tứ giác ADKE nội tiếp 0,25
b) Tia BD cắt đường tròn (O) tại I (I khác B). Chứng minh · · CIK = CKI. Nêu được · ·
EAD = CKI (vì tứ giác ADKE nội tiếp) b) 0,75 0,25 Và · ·
CIK = EAD (góc nội tiếp cùng chắn cung BC) 0,25 Suy ra · · CIK = CKI. 0,25
c) Gọi N là trung điểm của BC. Chứng minh ND là tiếp tuyến
của đường tròn ngoại tiếp tam giác ADE.
Chỉ ra được tâm đường tròn ngoại tiếp tam giác ADE là trung điể 0,1 m J của đoạn thẳng AK
Chứng minh được · · JDA = J D A và · · NDC = NCD. 0,1 c) 0,5 mà · · 0
JAD + NCD = 90 (do K là trực tâm của tam giác ABC). 0,1 · · 0 · 0
Þ JDA + NDC = 90 Þ NDJ= 90 0,1
Kết luận ND là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE 0,1
Tất cả các cách giải khác của học sinh nếu đúng thì người chấm cho điểm tương ứng với
hướng dẫn này Trang 8