Đề thi học kì 2 môn Toán lớp 11 năm 2023 - 2024 (Sách mới) | Chân Trời Sáng Tạo đề 1

MA TRẬN ĐỀ KIỂM TRA CUỐI KỲ 2
MÔN: TOÁN - LỚP 11 - CHÂN TRỜI SÁNG TẠO Chương/ Nội dung/
Mức độ đánh giá Tổng TT đơn vị kiến Nhận biết Thông hiểu Vận dụng
Vận dụng cao % điể Chủ đề m thức TN TL TN TL TN TL TN TL Phép tính luỹ thừa, phép tính lôgarit và các Hàm số tính chất. mũ và Hàm số mũ, 12 1 hàm số 4 2 hàm số (6 TN) lôgarit lôgarit. Phương trình, bất phương trình mũ và lôgarit Đạo hàm.Các Đạ TL 28 o quy tắc tính 2 hàm 5 4 1 (9 TN, đạo hàm. Đạo hàm cấ (1,0) 1 TL) p hai Biến cố giao và quy tắc Xác nhân xác suấ 21 t. TL 2 3 4 4 (8 TN, suất Biến cố hợp (0,5) và quy tắ 1 TL) c cộng xác suất Hai đường thẳng vuông góc. Đường thẳng vuông
Quan hệ góc với mặt vuông phẳng góc Hai mặt TL 39 4 TL 4 trong phẳng vuông 7 5 3 (12 TN, không góc (0,5) (1,0) 2 TL) gian Khoảng cách trong không gian. Góc giữa đường thẳng và mặt phẳng Tổng 20 15 2 2 Tỉ lệ % 40% 30% 20% 10% 100% Tỉ lệ chung 70% 30% 100%
BẢN ĐẶC TẢ ĐỀ KIỂM TRA CUỐI KỲ 2
MÔN: TOÁN - LỚP 11 - CHÂN TRỜI SÁNG TẠO
Số câu hỏi theo mức độ nhận Chương/chủ thức STT Thông đề Nội dung
Mức độ kiểm tra, đánh giá Nhận Vận Vận biêt hiểu dụng dụng cao Nhận biết:
– Nhận biết được khái niệm luỹ
Phép tính thừa với số mũ nguyên của một Câu 1 lũy thừ a
số thực khác 0; luỹ thừa với số
mũ hữu tỉ và luỹ thừa với số mũ
thực của một số thực dương. Nhận biết:
Phép tính – Nhận biết được khái niệm Câu lôgarit lôgarit cơ số 2 Hàm số
a (a > 0, a  1) của mũ một số thực dương. 1 và hàm số lôgarit Nhận biết: Hàm số
– Nhận biết được hàm số mũ và Câu mũ.Hàm hàm số 3- lôgarit. 4
số lôgarit – Nhận dạng được đồ thị của các
hàm số mũ, hàm số lôgarit. Phương Thông hiểu:
trình, bất – Giải được phương trình, bất Câu 5 phương
phương trình mũ, lôgarit ở - dạng trình mũ đơn giả 6 n. và lôgarit Nhận biết:
– Nhận biết được một số bài toán
dẫn đến khái niệm đạo hàm như:
xác định vận tốc tức thời của
một vật chuyển động không đều,
xác định tốc độ thay đổi của nhiệt độ.
– Nhận biết được định nghĩa đạo hàm.
– Nhận biết được ý nghĩa hình Câu
Đạo hàm học của đạo hàm. Câu 7 – 8-9
Nhận biết được số e thông qua 2 Đạo hàm
bài toán mô hình hoá lãi suất ngân hàng. Thông hiểu:
– Hiểu được công thức tính đạo
hàm của một số hàm đơn giản bằng định nghĩa.
– Thiết lập được phương trình
tiếp tuyến của đồ thị hàm số tại
một điểm thuộc đồ thị.
Các quy Nhận biết: Câu Câu TL tắc tính
- Nhớ các công thức đạo hàm đạo hàm 10-12 13-14 1*
của một số hàm số thường gặp,
đạo hàm của một số hàm số
lượng giác, hàm số mũ và hàm
số lôgarit, tính đạo hàm của
tổng, hiệu, tích, thương của hàm số. Thông hiểu:
– Tính được đạo hàm của một số
hàm số sơ cấp cơ bản (như hàm
đa thức, hàm căn thức đơn giản,
hàm số lượng giác, hàm số mũ, hàm số lôgarit). Vận dụng:
– Sử dụng được các công thức
tính đạo hàm của tổng, hiệu, tích,
thương của các hàm số và đạo hàm của hàm hợp. Nhận biết:
– Nhận biết được khái niệm đạo
hàm cấp hai của một hàm số. Thông hiểu
– Tính đạo hàm cấp hai của một vài hàm đơn giản
Đạo hàm Vận dụng: Câu TL cấp hai
– Giải quyết được một số vấn đề 15 1*
có liên quan đến môn học khác
hoặc có liên quan đến thực tiễn
gắn với đạo hàm cấp hai (ví dụ:
xác định gia tốc từ đồ thị vận tốc
theo thời gian của một chuyển
động không đều,...). Biến cố Nhận biết: giao và
– Nhận biết được một số khái Câu Câu quy tắc
niệm về xác suất cổ điển: hợp và nhân xác giao các biế 16-17 18-19
n cố; biến cố độc lập. suất Thông hiểu
– Hiểu các quy tắc tìm giao và hợp các biến cố. Vận dụng:
– Tính được xác suất của biến cố
hợp bằng cách sử dụng công 3 Xác suất thức cộng. Biến cố
– Tính được xác suất của biến cố hợp và
giao bằng cách sử dụng công Câu Câu quy tắc TL 2
thức nhân (cho trường hợp biến 20-21 22-23 cộng xác cố độc lập). suất
– Tính được xác suất của biến cố
trong một số bài toán đơn giản
bằng phương pháp tổ hợp.
– Tính được xác suất trong một
số bài toán đơn giản bằng cách
sử dụng sơ đồ hình cây. 4 Quan hệ
Hai đường Nhận biết: Câu vuông góc thẳng
– Nhận biết được khái niệm góc 24
trong không vuông góc giữa hai đường thẳng trong gian không gian.
– Nhận biết được hai đường
thẳng vuông góc trong không gian. Nhận biết:
– Nhận biết được đường thẳng
vuông góc với mặt phẳng.
– Nhận biết được khái niệm phép chiếu vuông góc.
– Nhận biết được công thức tính
thể tích của hình chóp, hình lăng trụ, hình hộ Đườ p. ng Thông hiểu: thẳng – Câu Câu vuông góc
Xác định được điều kiện để đườ
ng thẳng vuông góc với mặt 25 26 với mặt phẳng. phẳng
– Xác định được hình chiếu
vuông góc của một điểm, một
đường thẳng,một tam giác.
– Giải thích được được định lí ba đường vuông góc.
– Giải thích được được mối liên
hệ giữa tính song song và tính
vuông góc của đường thẳng và mặt phẳng. Thông hiểu:
– Xác định được điều kiện để hai mặt phẳng vuông góc.
– Giải thích được tính chất cơ Hai mặt
bản về hai mặt phẳng vuông góc. Câu phẳng – vuông góc
Giải thích được tính chất cơ 27
bản của hình lăng trụ đứng, lăng
trụ đều,hình hộp đứng, hình hộp
chữ nhật, hình lập phương, hình chóp đều. Nhận biết:
– Nhận biết được đường vuông
góc chung của hai đường thẳng chéo nhau. Thông hiểu: Khoảng
– Xác định được khoảng cách từ
cách trong một điểm đến một đường thẳng; Câu Câu không TL 4
khoảng cách từ một điểm đến 28-29 30-31 gian
một mặt phẳng; khoảng cách
giữa hai đường thẳng song song;
khoảng cách giữa đường thẳng
và mặt phẳngsong song; khoảng
cách giữa hai mặt phẳng song
song trong những trường hợp đơn giản. Vận dụng:
– Tính được khoảng cách giữa
hai đường thẳng chéo nhau trong
những trường hợp đơn giản (ví
dụ: có một đường thẳng vuông
góc với mặt phẳng chứa đường thẳng còn lại).
Vận dụng cao:
– Sử dụng được kiến thức về
khoảng cách trong không gian để
mô tả một số hình ảnh trong thực tiễn. Nhận biết:
– Nhận biết được khái niệm góc
giữa đường thẳng và mặt phẳng.
– Nhận biết được khái niệm góc
nhị diện, góc phẳng nhị diện. Thông hiểu:
– Xác định được góc giữa đường
thẳng và mặt phẳng trong những
trường hợp đơn giản (ví dụ: đã
biết hình chiếu vuông góc của
đường thẳng lên mặt phẳng). – Góc giữ
Xác định được số đo góc nhị a đườ
diện, góc phẳng nhị diện trong ng Câu Câu
những trường hợp đơn giản (ví TL 3 thẳng và 32-33 34-35
dụ: nhận biết được mặt phẳng
mặt phẳng vuông góc với cạnh nhị diện). Vận dụng:
– Tính được góc giữa đường
thẳng và mặt phẳng trong những
trườnghợp đơn giản (ví dụ: đã
biết hình chiếu vuông góc của
đường thẳng lên mặt phẳng).
– Tính được số đo góc nhị diện,
góc phẳng nhị diện trong những
trường hợp đơn giản (ví dụ: nhận
biết được mặt phẳng vuông góc với cạnh nhị diện). Tổng 20 15 2 2 Tỉ lệ % 40% 30% 20% 10% Tỉ lệ chung 70% 30%
KIỂM TRA CUỐI KÌ II NĂM HỌC 2023 – 2024 SỞ GD&ĐT…… MÔN TOÁN 11 - CTST TRƯỜNG THPT
Thời gian: 90 phút (không kể thời gian giao đề)
Họ và tên học sinh: ……………………………………………… Lớp: ……………..
PHẦN 1: TRẮC NGHIỆM (7 điểm).
Câu 1: Cho a  0 , b  0 và x , y là các số thực bất kỳ. Đẳng thức nào sau đúng? x  a  A. ( + )x x x
a b = a + b . B. x =   a . −x b . C. x+y x y a = a + a . D. x
a b = (ab)xy y .  b 
Câu 2: Giá trị của biểu thức là log 2 là: 4 3 1 A. 1. B. 2. C. . D. . 2 2
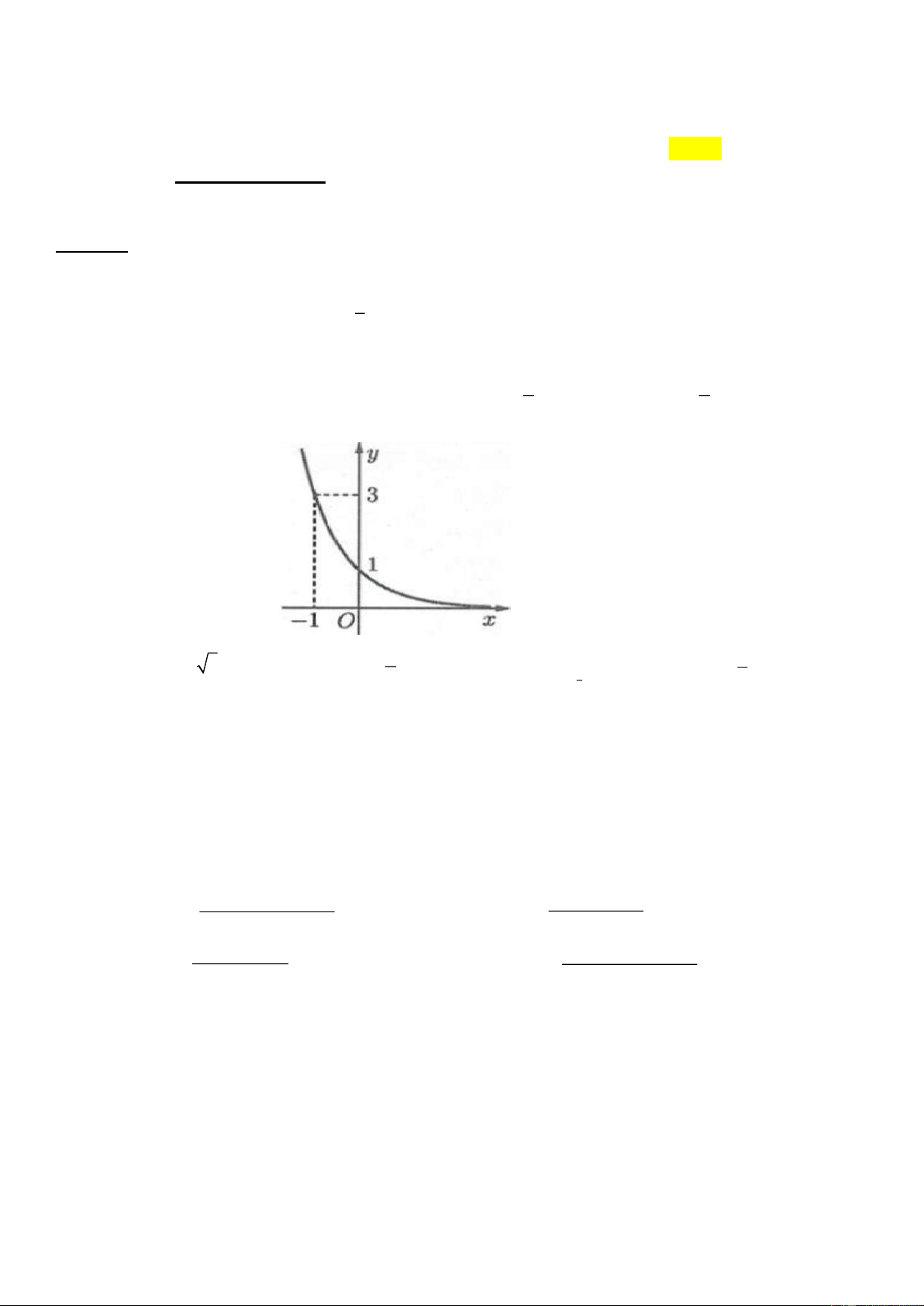
Câu 3: Đồ thị sau là của hàm số nào? x x x  1   1  A. y = ( 3) .
B. y =   .
C. y = log x . D. y = .    2  1  3  3
Câu 4: Trong các hàm số sau, hàm số nào là hàm số mũ? − A. 4 y = x . B. = ( )x y  .
C. y = log x .
D. y = ( x − ) 2 1 . 2
Câu 5: Nghiệm của phương trình log x −1 = 3 là: 2 ( ) A. x = 9. B. x = 8. C. x = 10. D. x = 7. Câu 6: −
Nghiệm của phương trình x 1 3 = 27 là
A. x = 4 .
B. x = 3 .
C. x = 2 . D. x = 1.
Câu 7:Giới hạn (nếu tồn tại) nào sau đây dùng để định nghĩa đạo hàm của hàm số y = f (x) tại x 1? 0 f (x + x  ) − f (x )
f (x) − f (x ) A. 0 lim . B. 0 lim . x  0 → x  x→0 x − x0
f (x) − f (x ) f (x + x  ) − f (x) C. 0 lim . D. 0 lim . x→ −  →  0 x x x x 0 x 0
Câu 8: Cho hàm số f (x) 2
= x +1. Tính đạo hàm của hàm số tại điểm x = 2 . 0 A. 3. B. 4. C. 2. D. 5.
Câu 9: Xét ba mệnh đề sau:
(1) Nếu hàm số f ( x) có đạo hàm tại điểm x = x thì f ( x) liên tục tại điểm đó. 0
(2) Nếu hàm số f ( x) liên tục tại điểm x = x thì f ( x) có đạo hàm tại điểm đó. 0
(3) Nếu hàm số f ( x) gián đoạn tại điểm x = x thì chắc chắn f ( x) không có đạo hàm tại 0 điểm đó. Trong ba mệnh trên: A. (1) và (3) đúng. B. (2) đúng. C. (1) và (2) đúng. D. (2) và (3) đúng.
Câu 10: Quy tắc tính đạo hàm nào sau đây là đúng?    
A. (u + v) = u + v .
B. (u + v) = u v
 + uv . C. (u + v) = u− v. D. (u + v) = u v −uv .
Câu 11: Hàm số y = x có đạo hàm trên khoảng (0;+) đạo hàm của hàm số y = x .    A. ( x ) 1 =
B. y = x . C. ( ) 1 x = . D. ( ) 2 x = . 2 x x x
Câu 12: Trong các công thức sau, công thức nào đúng? A. ( x)' sin = cos . x B. ( x)' sin = −cos . x C. ( x)' cos = sin . x D. ( x)' sin = sin . x
Câu 13: Hàm số f (x) 4 3 2
= −x + 4x − 3x + 2x +1 xác định trên . Giá trị f '(− ) 1 bằng: A. 4 . B. 14 . C. 15 . D. 24 .
Câu 14: Tính đạo hàm của hàm số 2023x y = ? A. ' 2023 . x y = B. ' x 1 y 2023 − = . C. ' x 1 y 2023.2023 − = . D. ' 2023x y = ln 2023.
Câu 15: Đạo hàm cấp hai của hàm số ( ) 2
f x = x bằng biểu thức nào sau đây? A. 2 . B. x . C. 3 . D. 2x .
Câu 16: Cho A và B là 2 biến cố độc lập với nhau. Khi đó P( . A B) = P ( A)
A. P ( A) + P (B)
B. P ( A).P ( B)
C. P ( A) − P (B) D. P ( B)
Câu 17: Khẳng định nào sau đây là ĐÚNG:
A. Cho hai biến cố A và B . Biến cố " A hoặc B xảy ra", kí hiệu là A B , được gọi là
biến cố giao của A và B .
B. Cho hai biến cố A và B . Biến cố " A hoặc B xảy ra", kí hiệu là A B , được gọi là biến
cố hợp của A và B .
C. Cho hai biến cố A và B . Biến cố " A hoặc B xảy ra", kí hiệu là A B , được gọi là
biến cố hợp của A và B .
D. Cho hai biến cố A và B . Biến cố " A hoặc B xảy ra", kí hiệu là A B , được gọi là biến cố xung khắc.
Câu 18: Cho A và B là 2 biến cố độc lập với nhau, P(A) = 0,4; P(B) = 0,3. Khi đó P(A.B) bằng A. 0,58 B. 0,7 C. 0,1 D. 0,12
Câu 19: Cho A và B là 2 biến cố độc lập với nhau, P(A) = 0,4; P(A.B) = 0,15. Khi đó P(B) bằng A. 0,5. B. 0,55. C. 0,06. D. 0,25.
Câu 20: Một hộp chứa 5 viên bi xanh và 3 viên bi đỏ có cùng kich thước và khối lượng. Lấy ra ngẫu
nhiên đồng thời 2 viên bi từ hộp. Gọi A là biến cố "Hai viên bi lấy ra đều có màu xanh", B
là biến cố "Hai viên bi lấy ra đều có màu đỏ". Mô tả bằng lời biến cố A B
A. "Hai viên bi lấy ra có cùng màu"
B. "Hai viên bi lấy ra có khác màu"
C. "Hai viên bi lấy ra có màu bất kì"
D. "Hai viên bi lấy ra chỉ có màu xanh"
Câu 21: Cho A , B là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
A. P ( A  B) = P ( A) + P ( B)
B. P ( A  B) = P ( A).P (B)
C. P ( A B) = P ( A) − P (B)
D. P ( A  B) = P ( A) + P ( B) Câu 22: Cho ,
A B là hai biến cố xung khắc. Biết P( ) 1 A =
, P( A B) 1 = . Tính P(B). 5 3 3 8 2 1 A. . B. . C. . D. . 5 15 15 15 Câu 23: 1 1
Cho A, B là hai biến cố xung khắc. Biết P(A ) = ,P(B) = . Tính P(A  B) 3 4 7 1 1 1 A. B. C. D. 12 12 7 2
Câu 24: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song
song với đường thẳng còn lại.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Câu 25: Khẳng định nào sau đây sai?
A. Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong ( ) thì d vuông
góc với bất kì đường thẳng nào nằm trong ( )
B. Nếu đường thẳng d ⊥ ( ) thì d vuông góc với hai đường thẳng trong ( )
C. Nếu đường thẳng d vuông góc với hai đường thẳng nằm trong ( ) thì d ⊥ ( )
D. Nếu d ⊥ ( ) và đường thẳng a / / ( ) thì d ⊥ a
Câu 26: Cho hai đường thẳng phân biệt a,b và mặt phẳng (P) trong đó a ⊥ (P) . Chọn mệnh đề sai trong các mệnh đề sau?
A. Nếu b ⊥ ( P) thì a//b
B. Nếu b//a thì b ⊥ ( P)
C. Nếu b  ( P) thì b ⊥ a
D. Nếu a ⊥ b thì b// ( P)
Câu 27: Trong các mệnh đề sau, mệnh đề nào sai?
A. Cho đường thẳng a vuông góc với đường thẳng b và b nằm trong mặt phẳng ( P) . Mọi
mặt phẳng (Q) chứa a và vuông góc với b thì ( P) vuông góc với (Q) .
B. Nếu đường thẳng a vuông góc với đường thẳng b và mặt phẳng ( P) chứa a , mặt phẳng
(Q) chứa b thì (P) vuông góc với (Q) .
C. Cho đường thẳng a vuông góc với mặt phẳng ( P) , mọi mặt phẳng (Q) chứa a thì ( P)
vuông góc với (Q) .
D. Qua một điểm có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
Câu 28: Đường vuông góc chung của hai đường thẳng chéo nhau a và b là:
A. Đường thẳng vừa vuông góc với a và vuông góc với b
B. Đường thẳng vừa vuông góc, vừa cắt hai đường thẳng chéo nhau a và b
C. Đường thẳng vuông góc với a và cắt đường thẳng b
D. Đường thẳng vuông góc với b và cắt đường thẳng a
Câu 29: Cho khối chóp diện tích đáy bằng S và chiều cao h . Khi đó thể tích V của khối chóp bằng: 1 A. V = S.h B. 1 V = S.h
C. V = S.h D. 1 V = S.h 2 3 6
Câu 30: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = a 2 . Cạnh bên SA = 2a và
vuông góc với mặt đáy ( ABCD) . Tính khoảng cách d từ D đến mặt phẳng (SBC) (SBC). a 10 2a 3 a 3 A. d = .
B. d = a 2 . C. d = D. d = 2 3 3
Câu 31: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với
mặt phẳng đáy và SA = a 2. Tính thể tích V của khối chóp S.ABC . D 3 a 2 3 a 2 3 a 2 A. V = . B. V = . C. 3
V = a 2. D. V = . 6 4 3
Câu 32: Khẳng định nào ĐÚNG trong các khẳng định sau:
A. Nếu đường thẳng a cắt một đường thẳng d  ( P) thì góc giữa a và d là góc giữa
đường thẳng a và (P) .
B. Nếu đường thẳng a không vuông góc với (P) thì góc giữa a và hình chiếu a của a trên
(P) gọi là góc giữa đường thẳng a và (P) .
C. Nếu đường thẳng a vuông góc với đường thẳng d  ( P) thì góc giữa a và d là góc giữa
đường thẳng a và (P) .
D. Nếu đường thẳng a song song với đường thẳng d  ( P) thì góc giữa a và d là góc giữa
đường thẳng a và (P) .
Câu 33: Nếu đường thẳng a vuông góc với mặt phẳng (P) . Khi đó ( ; a ( P)) = ? A. 0 . B. 180 . C. 90 . D. 45 .
Câu 34: Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy. Góc giữa đường
thẳng SC và mặt phẳng ( ABCD) là: A. SCB . B. CAS . C. SCA . D. ASC .
Câu 35: Cho hình chóp S.ABCD có đáy là hình vuông, SB vuông góc với đáy, gọi O = BD CA .
Góc giữa đường thẳng SO và mặt phẳng ( ABCD) là: A. SOB . B. SOA . C. SBO . D. OSB .
PHẦN 2: TỰ LUẬN (3 điểm).
Câu 1: Tính đạo hàm các hàm số sau: a) 5
y = x − cos x − 7 . b) y = ( x + )11 3 4 .
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , BC = a 3 , AC = 2a . Cạnh bên
SA vuông góc với mặt phẳng đáy và SA = a 3 . Tính góc giữa đường thẳng SB và mặt phẳng đáy.
Câu 3: Một hộp đựng 40 viên bi trong đó có 20 viên bi đỏ, 10 viên bi xanh, 6 viên bi vàng, 4 viên
bi trắng. Lấy ngẫu nhiên hai bi, tính xác suất biến cố A : “hai viên bi cùng màu”.
Câu 4: Kim tự tháp Giza là Kim tự tháp Ai Cập lớn nhất và là lăng mộ của Vương triều thứ Tư của
pharaoh Khufu. Được xây dựng vào đầu thế kỷ 26 trước Công nguyên trong khoảng thời gian 27
năm, đây là kim tự tháp lâu đời nhất còn nằm trong Bảy kỳ quan của thế giới cổ đại, và là kim tự tháp
duy nhất với phần lớn còn nguyên vẹn. Kim tự tháp này được xây dựng theo mô hình là hình chóp tứ
giác đều với kích thước như sau: chiều cao xấp xỉ 138m , độ dài đáy xấp xỉ 230m (theo số liệu mới
nhất trên https://vi.wikipedia.org/wiki/). Tính khoảng cách từ tâm của đáy kim tự tháp đến mặt bên.
------------------------- HẾT ------------------------- HƯỚNG DẪN CHẤM I. PHẦN TRẮC NGHIỆM 1.D 2.D 3.D 4.B 5.A 6.A 7.C 8.B 9.A 10.A 11.A 12.A 13.D 14.D 15.A 16.D 17.C 18.D 19.A 20.A 21.A 22.C 23.A 24.D 25.C 26.D 27.B 28.B 29.B 30.C 31.D 32.B 33.C 34.C 35.A II. PHẦN TỰ LUẬN
Câu 1: Tính đạo hàm các hàm số sau: a) 4
y ' = 5x + sin x . b) y = ( x − )10 ' 33 3 5 . Câu 2:
+ Ta có: (SB,(ABC)) = (SB, BA) = SBA =  + Tính: tan = SA . AB
+ Tính: AB = AC − BC = ( a) − (a )2 2 2 2 2 2 3 = a = a . SA a 3 Suy ra: tan 3  60 = = =  = . AB a
Vậy góc giữa đường thẳng SB và mặt phẳng đáy bằng 60 . Câu 3: Ta có: n() 2 = C 40 Gọi các biến cố:
D : “lấy được 2 bi viên đỏ” ta có: 2 n = C = 90 ; D 20
X : “lấy được 2 bi viên xanh” ta có: 2 n = C = 45 ; X 10
V : “lấy được 2 bi viên vàng” ta có: 2 n = C = 15 ; V 6
T : “ lấy được 2 bi màu trắng” ta có: 2 n = C = 6 . T 24
Ta có D, X ,V ,T là các biến cố đôi một xung khắc và A = D  X V V T . 256 64
P ( A) = P (D) + P ( X ) + P (V ) + P (T ) = = . 2 C 195 40 Câu 4:
Ta mô hình kim tự tháp như hình vẽ, là hình chóp tứ giác đều SABCD .
Gọi O = BD  AC  SO ⊥ ( ABCD) , K là trung điểm AB .
Ta có OK //AD, AD ⊥ AB  OK ⊥ AB Kẻ OH ⊥ SK Ta có: AB ⊥ OK 
 AB ⊥ (SOK )  AB ⊥ OH AB ⊥ SO O  H ⊥ AB 
 OH ⊥ (SAB)  d (O,(SAB)) = OH O  H ⊥ SK 1 1 1 1 1 17 = + = + = . 2 2 2 2 2 OH SO OK 138 230 238050
 OH 118,33m .
------------------------- HẾT -------------------------