SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2019 – 2020 TP. HỒ CHÍ MINH MÔN TOÁN – LỚP 11
TRƯỜNG THCS-THPT DIÊN HỒNG
Thời gian làm bài: 90 phút (không kể thời gian phát đề) ĐỀ CHÍNH THỨC (Đề thi gồm 01 trang)
Câu 1: (2.0 điểm) Tính các giới hạn sau: 6x  2  3x 1 a/ lim b/       2 lim x 4x 5 x x  x 1  x 1 Câu 2: (1.0 điểm) 3  x  8  khi x  2
Tìm m để hàm số f  x 2  2x  x  6 liên tục tại x  2 . 0  mx 1 khi x  2 Câu 3: (2.0 điểm)
Tính đạo hàm của các hàm số sau: 2 x  4x 1 a/ 4 2 y  x  3x  4 b/ y   x  x5 2sin 3cos c/ y  2x 1 Câu 4: (0.5 điểm)
Chứng minh rằng phương trình m x  2020 x  2019 2019 . 2020
 2x  4039  0 luôn có
nghiệm với mọi tham số m. Câu 5: (1.0 điểm)
Viết phương trình tiếp tuyến của đồ thị hàm số C 3 2
: y  x  3x  2 biết tiếp tuyến vuông góc
với đường thẳng d  1 : y  x  2020 . 3
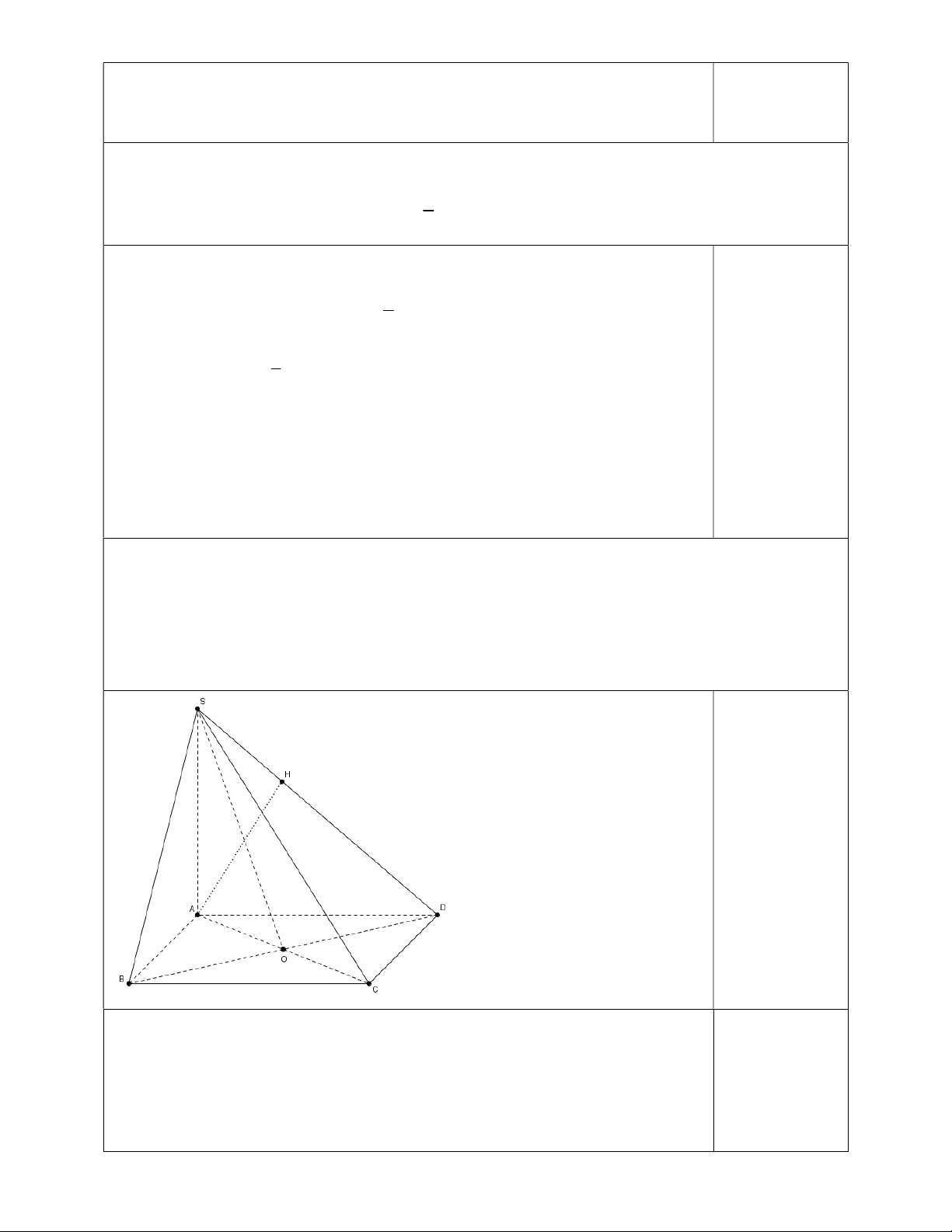
Câu 6: (3.5 điểm) Cho hình chóp S.ABCD có đáy là hình vuông tâm O với độ dài cạnh là 2a . Cạnh bên
SA vuông góc đáy có độ dài SA  3a .
a/ Chứng minh rằng: BC  SAB và SBD  SAC .
b/ Xác định và tính góc giữa SO và mặt đáy (ABCD).
c/ Xác định và tính khoảng cách từ điểm B đến (SCD).
-----------  HẾT  -----------
Học sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên học sinh: .......................................................................................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ II – NĂM HỌC 2019 – 2020 TP. HỒ CHÍ MINH MÔN TOÁN – LỚP 11
TRƯỜNG THCS-THPT DIÊN HỒNG
Thời gian làm bài: 90 phút (không kể thời gian phát đề) ĐIỂM TỪNG NỘI DUNG TRẢ LỜI PHẦN
Câu 1: (2.0 điểm) Tính các giới hạn sau: 6x  2  3x 1 a/ lim x 1  x 1 6x  2  3x 1 a/ lim x 1  x 1 0,25 6x  2  3x   1  lim 0,25 x 1  x   1  6x  2  3x 1 3x  3 0,25  lim x 1  x   1  6x  2  3x 1 0,25 3 x   1  lim x 1  x   1  6x  2  3x 1 3 3 3  lim   x 1  6x  2  3x 1 2  2 4 b/       2 lim x 4x 5 x x  2 2 x  4x  5  x  lim x  2 x  4x  5  x 0,25  5  x 4   2  0,25 lim  x   x  4 5 x 1   x 2 x x 0,25 5 4  2 4  lim x   2  0,25 x  4 5 2   1  1 2 x x 3  x  8  khi x  2
Câu 2: (1.0 điểm) Tìm m để hàm số f  x 2  2x  x  6 liên tục tại x  2 . 0  mx 1 khi x  2 Ta có: f 2  2m 1 0,25
lim f  x  lim mx   1  2m 1 0,25 x 2 x 2   x  8 x  2 2 3 x  2x  4 2   0,25 f  x x 2x 4 12 lim  lim  lim  lim    2 x 2 x 2   x 2 2x x 6  x  22x 3 x 2     2x  3 7 12 5 0,25
Hàm số liên tục tại x  2 nên 2m 1   m  . 0 7 14
Câu 3: (2.0 điểm) Tính đạo hàm của các hàm số sau: 2 x  4x 1 a/ 4 2 y  x  3x  4 b/ y   x  x5 2sin 3cos c/ y  2x 1 a/ 4 2 y  x  3x  4 0.25 0.25 3  y'  4x  6x b/ y   x  x5 2sin 3cos 0,25  y   x  x4  x  x/ ' 5 2sin 3cos 2sin 3cos 0,25  y   x  x4 ' 5 2sin 3cos 2cos x 3sin x 0,25 2 x  4x 1 c/ y  2x 1 
x  4x 1/ 2x   1  2x  / 2 2 1 x  4x 1  y '   0.25 2x  2 1 2x  4 2x   2 1  2 x  4x 1 2 2 x  4x 1  y '   2x  2 1 0.25 x  22x   1  2 2 x  4x   1  y '  2x  2 2 1 x  4x 1 2 2
2x  5x  2  2x  8x  2 3x  4 0.25  y '   2x  2 1 x  4x 1 2x  2 2 2 1 x  4x 1
Câu 4: (0.5 điểm) Chứng minh rằng phương trình m x  2020 x  2019 2019 . 2020  2x  4039  0
luôn có nghiệm với mọi tham số m. Xét f  x  m x  2020 x  2019 2019 . 2020  2x  4039 0,25 TXĐ: D = R.  f  2019  1 Ta có: 
 f 2019. f 2020     f    1 0 2020  1
Vì hàm số liên tục trên R nên liên tục trên 2019;2020
Suy ra phương trình f  x  0 luôn có ít nhất một nghiệm thuộc 2019;2020 . 0,25
Cuối cùng phương trình f  x  0 luôn có nghiệm với mọi m.
Câu 5: (1.0 điểm) Viết phương trình tiếp tuyến của đồ thị hàm số C  3 2
: y  x  3x  2 biết tiếp
tuyến vuông góc với đường thẳng d  1 : y  x  2020 . 3 Đạo hàm 2 y '  3x  6x
Vì tiếp tuyến vuông góc với d  1 : y  x  2020 nên 3 0,25 k k    y x
   y x    x  x    x  x   tt d  1 . 1 ' . 1 ' 3 3 6 3 3 6 3 0 0   0 2 2   0 0 0 0 3 0,25  x 1 y  0 0,25 0 0
Viết phương trình tiếp tuyến của đồ thị tại điểm M 1;0 0,25
: y  y' 1x  1 0   : y  3  x  3
Câu 6: (3.5 điểm) Cho hình chóp S.ABCD có đáy là hình vuông tâm O với độ dài cạnh là 2a . Cạnh
bên SA vuông góc đáy và độ dài SA  3a .
a/ Chứng minh rằng: BC  SAB và SBD  SAC .
b/ Xác định và tính góc giữa SO và mặt đáy (ABCD).
c/ Xác định và tính khoảng cách từ điểm B đến (SCD).
a/ Chứng minh rằng: BC  SAB và SBD  SAC . BC  AB 0,25  Ta có: 0,25 BC  AB 0,25  BC  SAB BD  AC Ta có:  0,25 BD  SA 0,25  BD  SAC 0,25 Ma` BD  SBD  SBD  SAC
b/ Xác định và tính góc giữa SO và mặt đáy (ABCD).
Ta có: hình chiếu vuông góc của SO lên (ABCD) là AO. 0,25  S ; O   ABCD  SOA  0,25
Xét tam giác SAO vuông tại A có 0,25 SA 3a 3 0 tan S  OA     S  OA  64,76 AO a 2 2 0,25
c/ Xác định và tính khoảng cách từ điểm B đến (SCD). 0,25
Vì AB // (SCD) suy ra d B;SCD  d  ; A SCD     .
Trong mp(SAD), kẻ AH  SD tại H. 0.25 AH  SD Khi đó 
 AH  SCD  AH  d  ; A  SCD AH CD  
Xét tam giác SAD vuông tại A có S . A AD 3 . a 2a 6 13 0,25 AH.SD  S . A AD  AH    a 2 2 SA  AD  a2  a2 13 3 2 Vậy d B  SCD 6 13 ;   a  13 0,25 HẾT