SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KÌ II
THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2019-2020 TRƯỜNG TH, THCS VÀ THPT QUỐC TẾ Á CHÂU ĐỀ CHÍNH THỨC MÔN: TOÁN - KHỐI 11
(Thời gian: 90 phút, không tính thời gian giao đề)
_____________________________________________________________________
Họ tên học sinh: ----------------------------------------------Lớp: -------------- SBD: ---------
(Học sinh lưu ý làm bài trên giấy thi, không làm trên đề)
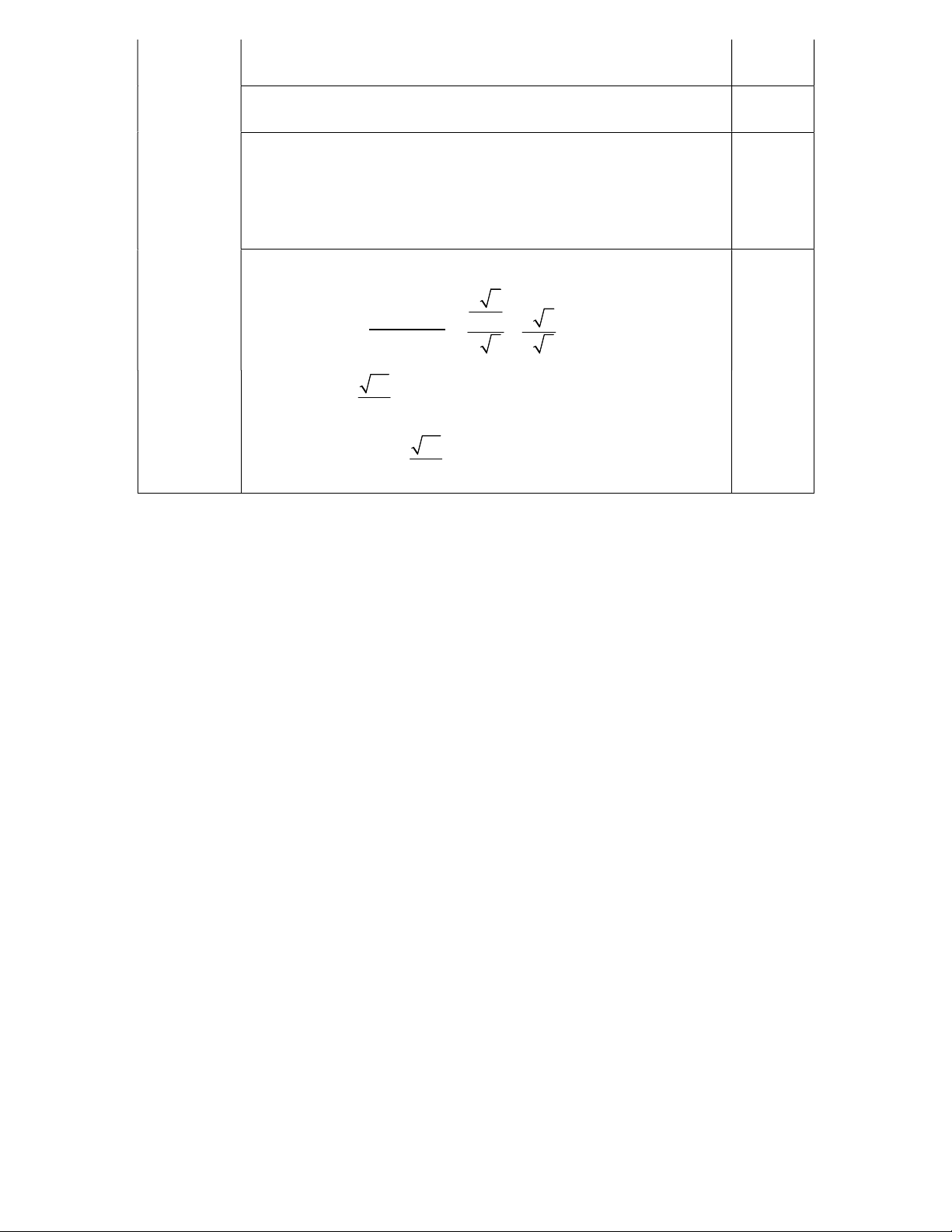
Câu 1: (2,5 điểm) Tìm các giới hạn sau 3 2 x  x  x 1 a) lim 2 x 1  x  3x  2 2  b) 3x 1 lim 4 2 x 6  x  x  2 c)      2 3 3 lim x 1 x 1 x 
Câu 2: (1,5 điểm) Xét tính liên tục của hàm số sau: 𝑥 − 5 ; 𝑛ế𝑢 𝑥 > 5
𝑓(𝑥) = √2𝑥 − 1 − 3 𝑡ạ𝑖 𝑥 = 5
(𝑥 − 5) + 3 ; 𝑛ế𝑢 𝑥 ≤ 5
Câu 3: (2,0 điểm) Tìm đạo hàm của các hàm số sau: a) 1 4 3 y  2x  x  2 x  5 3  b) 1 x y  1 x
Câu 4: (1,0 điểm) Viết phương trình tiếp tuyến của đường cong (C) có phương trình 3x  2 y 
, biết tiếp tuyến vuông góc với đường thẳng Δ: 4x – y + 10 = 0 x 1
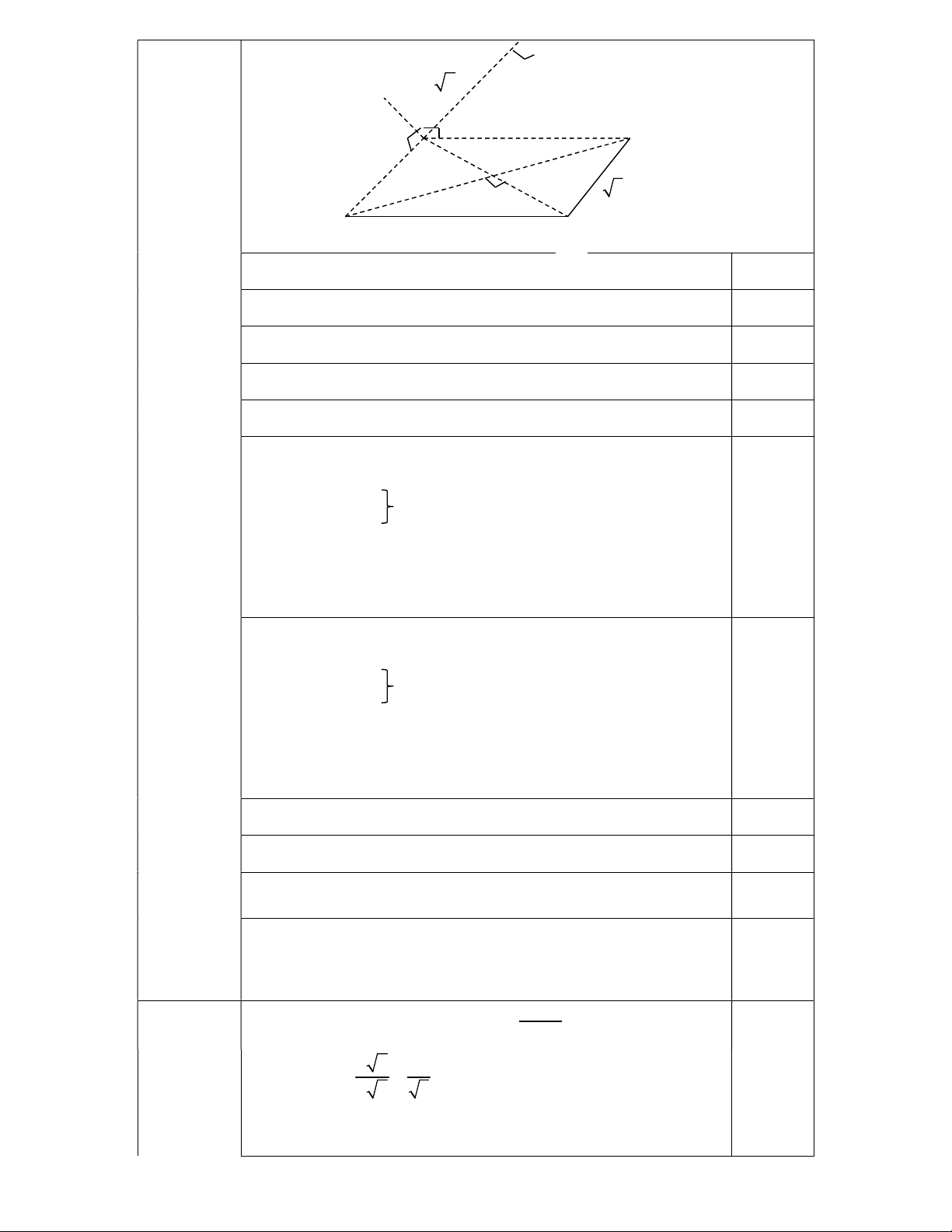
Câu 5: (3,0 điểm) Cho hình chóp S.ABCD; ABCD là hình vuông tâm O cạnh a 3 .
Cạnh bên SA vuông góc với mặt phẳng (ABCD) và SA = a 2 a) Chứng minh: BD ⊥ (SAC)
b) Gọi H, K lần lượt là hình chiếu của A lên SB và SD. Chứng minh: HK ⊥ SC
c) Tính góc giữa đường thẳng SC và mặt phẳng (ABCD)
d) Tính sin của góc giữa đường thẳng SB và mặt phẳng (SAC) ---HẾT---
Học sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2019-2020 MÔN: TOÁN 11 Câu Nội dung trả lời Điểm Câu 1 3 2 a) x  x  x 1 lim 2 (1.0) (2.5 điểm) x 1  x  3x  2 2 0.25 (x 1)(x 1)  lim x 1  (x  2)(x 1) 0.25 2 x 1  lim 0.25 x 1  x  2 = 0 0.25 2 b) 3x 1 lim (1.0đ) 4 2 x 6  x  x  2 2  1  0.25 x 3   2   x lim   x 4  1 2  x 6     2 4   x x  0.25 1 3  2  lim x 0.25 x 2  1 2  x 6     2 4   x x  = 0 0.25 c)    (0.5đ)   2 3 3 lim x 1 x 1 x          2 x x  3 3 lim 1 lim x x 1 x x   lim x   x   x  1 2 1  lim 0 x 2 x 1  x  lim x  x    x  1 3 3 1 lim 0 x 3 0.25 x  . x x 1   3 x 12 2 3 3  lim f (x)  0 0.25 x Câu 2 f (5) = (5 – 5)2 + 3 = 3 0.25 (1.5 điểm) lim f (x)  3 0.25 x 5  x  5 lim  lim x 5 x 5   2x 1  3 (x  5)( 2x 1  3)  lim x 5  2x 10 2x 1  3  lim 0.25 x 5  2 lim f (x)  3 0.25 x 5 
Vì lim f (x)  lim f (x)  f (5)  3 0.25 x 5 x 5  
⇒ Hàm số liên tục tại xo = 5 0.25 Câu 3 a) 1 4 3 y  2x  x  2 x  5 (1.0đ) 3 (2.0 điểm) 1 3 2 y '  8x  x   0 0.25 x 4 x b) 1 x y  (1.0đ) 1 x
1 x' 1 x  (1 x) 1 x' y '  0.25 1 x 1 x 1 x  2 1 x  0.5 1 x 3  x y '  0.25 2(1 x) 1 x Câu 4 1  f '(x)  x  2 0.25 (1.0 điểm) 1 Δ: y = 4x + 10 → kΔ = 4 τt ⊥ Δ ⇒ f '(x ).4  1  o  7 x  3; y  1  f x    x     o  o  0 o 2 2 '( ) 1 4 0.25 4 5 x  1  ; y  0 o  2
Pt τt của (C) tại  7  1 17 3; : y   x    0.25  2  4 4 Pt τt của (C) tại  5  1 9 1; : y   x    0.25  2  4 4 Câu 5 S (3.0 điểm) K H a 2 D A O a 3 B C a) CM: BD ⊥ (SAC) (1.0đ)
BD ⊥ AC (2 đường chéo hình vuông ABCD) (1) 0.25
BD ⊥ SA (do SA ⊥ (ABCD)) (2) 0.25 (1), (2) ⇒ BD ⊥ (SAC) 0.5 b) CM: HK ⊥ SC (1.0đ) (*) AH ⊥ SB (1) BC ⊥ BA (gt)
⇒BC ⊥ (SAB) ⇒ BC ⊥ AH (2) BC ⊥ SA (gt) 0.25 (1), (2) ⇒ AH ⊥ (SBC) ⇒ AH ⊥ SC (3) (*) AK ⊥ SD (4) CD ⊥ AD (gt)
⇒CD ⊥ (SAD) ⇒ CD ⊥ AK (5) CD ⊥ SA (gt) (4), (5) ⇒ AK ⊥ (SCD) ⇒ AK ⊥ SC (6) 0.25 (*) (3), (6) ⇒ SC ⊥ (AHK) 0.25 ⇒ SC ⊥ HK 0.25 c) Tính SC ABCD   ,( ) (0.5đ)
AC là hình chiếu vuông góc của SC trên (ABCD) SC ABCD    CA CS  ,( ) , 0.25 ΔSAC vuông tại A: tan đố 𝐴𝐶𝑆 = ề tan  a 2 1 ACS   a 6 3  30o SCA     ,( ) 30o SC ABCD  0.25 d) Tính SB SAC   ,( ) (0.5đ) O là tâm hình vuông ABCD
SO là hình chiếu vuông góc của SB trên (SAC) 0.25 SB SAC    SB SO  ,( ) , ΔSOB vuông tại O a 6 đố sin 𝐵𝑆𝑂 = a 6 2   ề a 5 2 5  30 BSO  arcsin 10 SB SAC   30 ,( )  arcsin 0.25 10 ---HẾT---