TRƯỜNG TRUNG HỌC THỰC HÀNH SÀI GÒN
ĐỀ KIỂM TRA HỌC KỲ II ĐỀ CHÍNH THỨC NĂM HỌC: 2019 – 2020 MÔN: TOÁN – LỚP: 11 (Đề thi có 01 trang)
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Họ và tên thí sinh: …………………………………………. Số báo danh: …………………………. ĐỀ BÀI
Câu 1 (1,0 điểm). Xét tính liên tục của hàm số y  f x  tại x0  2, biết: 1 2x  3  f x   khi x  2   2  x  2  x  3 khi x  2 
Câu 2 (3,0 điểm). Tính đạo hàm của các hàm số sau: 3 2x a) 2 y   x  3x  3 ; 3 b) y   x   2 5 9 x  4x  7 ; sinx  cosx c) y  . sinx  cosx
Câu 3 (1,0 điểm). Cho đường cong (C ) có phương trình 3
y  x  3x  1. Viết phương
trình tiếp tuyến của (C ) biết tiếp tuyến đó song song với đường thẳng d : y  9x  15.
Câu 4 (1,0 điểm). Quãng đường chuyển động của một chất điểm được biểu thị bởi công thức s t  3 2
 t  3t  9t  2, trong đó t  0, t tính bằng giây và s tính bằng mét.
a) Hãy xác định vận tốc tức thời và gia tốc tức thời của chất điểm tại thời điểm .t
b) Tính gia tốc của chất điểm tại thời điểm vận tốc triệt tiêu.
Câu 5 (4,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm , O SA vuông
góc với mặt phẳng (ABCD). Biết AB  a, SA  a 6.
a) Chứng minh rằng BD  (SAC ) và (SAB)  (SBC ).
b) Tính góc giữa đường thẳng SB và mặt phẳng (SAC ).
c) Tính theo a khoảng cách từ điểm A đến mặt phẳng (SBD).
d) Tính góc giữa hai mặt phẳng (SBC ) và (SCD). ____HẾT____
TRƯỜNG TRUNG HỌC THỰC HÀNH SÀI GÒN
ĐỀ KIỂM TRA HỌC KỲ II ĐÁP ÁN ĐỀ CHÍNH THỨC NĂM HỌC: 2019 - 2020 MÔN: TOÁN - LỚP: 11 (Đáp án có 04 trang)
Thời gian làm bài: 90 phút
(không kể thời gian phát đề) Câu Đáp án Điểm Câu 1 (1,0 điểm).
Xét tính liên tục của hàm số y  f  x tại x  2, biết: 0 1 1   2x  3   f  x khi x 2   2  x  2 x  3 khi x  2    f      x 1 2x 3 22 x 2 lim lim lim lim 1 0,5 x 2 x 2 x 2 2  x
 2  x1 2x 3 x 2     1 2x  3 lim f  x  lim  2 x  3  1; f  0,25   2 1 x2 x2
Vậy lim f  x  lim f  x  f
nên hàm số đã cho liên tục tại x  2 0,25   2 0 x2 x2
Câu 2 (3,0 điểm). Tính đạo hàm của các hàm số sau: 2 3 2x a) 2 y   x  3x  3 3 3 2x a) 2 y   x  3x  3 0,5 3 +0,25x2 2 y '  2x  2x  3 b) y   x   2 5 9 x  4x  7 y   x   2 5 9 x  4x  7  y  5x  9 2
x  4x  7  5x  9 2x  4x  7 0,25 + x  2 0,25x2 2
y  5 x  4x  7  5x  9  2 x  4x  7 + 0,25 2 10x  21x 17 y  2 x  4x  7 sin x  cos x c) y  sin x  cos x sin x  cos x y  0,25x4 sin x  cos x
sin x cos xsin x cos x sin x cos xsin x cos x      y  sin x  cos x2
sin x  cos x2  sin x  cos x2 y   sin x  cos x2 2 2 2 sin x  cos x 2 y   sin x  cos x2 sin x  cos x2 Câu 3 (1,0 điểm). 3
Cho đường cong C  y  f  x 3 :
 x  3x 1. Viết phương trình tiếp tuyến của C
biết tiếp tuyến đó song song với đường thẳng d  : y  9x 15. 3 y  x  3x 1 TXĐ: D  R 0,25 y  f  x 2  3x  3
Đường thẳng d  : y  9x 15 có hệ số góc là 9.
Gọi x là hoành độ tiếp điểm, ta có: 0 0,25 f  x  2
 9  3x  3  9  x  2 0 0 0
Phương trình tiếp tuyến tại x  2 : y  3  9 x  2  y  9x 15 (loại) 0   0,25
Phương trình tiếp tuyến tại x  2
 : y 1  9 x  2  y  9x 17 (nhận) 0   0,25 Câu 4 (1,0 điểm).
Quãng đường chuyển động của một chất điểm được biểu thị bởi công thức 4 s t 3 2
 t  3t  9t  2, trong đó t  0, t tính bằng giây và s tính bằng mét.
a) Hãy xác định vận tốc tức thời và gia tốc tức thời của chất điểm tại thời điểm t.
Vận tốc tức thời của chất điểm tại thời điểm t v t  st 2 :  3t  6t  9m/s 0,25x2
Gia tốc tức thời của chất điểm tại thời điểm t a t   s t  t   2 : 6 6 m/s 
b) Tính gia tốc của chất điểm tại thời điểm vận tốc triệt tiêu.   v t t 3 2
 0  3t  6t  9  0   t  3  t  1  0 0,25x2
Khi đó gia tốc của chất điểm là a     2 3 12 m/s  Câu 5 (4,0 điểm). 5
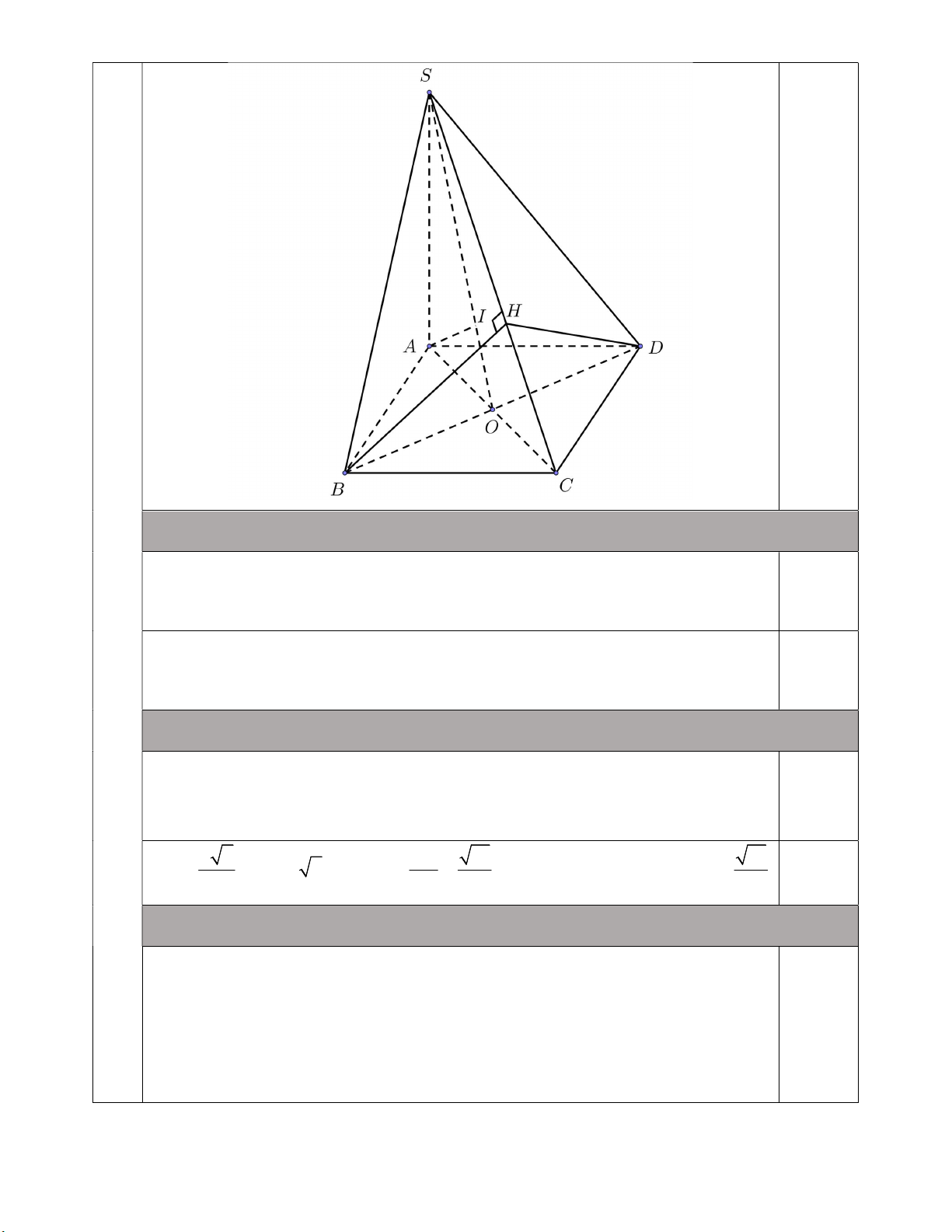
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA vuông góc với mặt
phẳng  ABCD. Biết AB  a, SA  a 6.
a) Chứng minh rằng BD  SAC và SAB  SBC. BD  AC  hv ABCD    0,5 BD  SA  SA   ABCD BD SAC BC  AB  hv ABCD      0,5 BC  SA  SA  
ABCD BC SAB SBC SAB
b) Tính góc giữa đường thẳng SB và mặt phẳng SAC .
BD  SAC tại O  SO là hình chiếu của SB lên mặt phẳng SAC. 0,25 Do đó SB,SAC   SB,SO   BSO a 2 BO  SB  a  BO 14 BSO    SB SAC    14 ; 7;sin , BSO  arcsin 0,25x3 2 SB 14 14
c) Tính khoảng cách từ điểm A đến mặt phẳng SBD.
Trong SAC, dựng AI  SO tại I. AI  SO     tại I. 0,5 AI  BD  BD   SAC AI SBD
Vậy độ dài AI là khoảng cách từ điểm A đến mặt phẳng SBD. a 2 a 26 a 6  S . A AO a 78 SO  ; 2 AI    0,25x2 2 SO a 26 13 2
d) Tính góc giữa hai mặt phẳng SBC và SCD.
Trong SBC , dựng BH  SC tại H   1 SC  BH   tại H 2      
  SC  BDH   SC  BH SC BD BD SAC 0,25
SBCSCD  SC3  
1 ,2,3  SBC,SCD   BH,DH  a 14 HB  HD  ; BD  a 2 14 2 14a 2 2.  2a 0,25x2  2 2 2 HB  HD  BD 1 16  cos BHD    2.H . B HD 7 2 7 a 4 SBC SCD  1 ,     arccos 0,25 7
Ghi chú: Học sinh giải cách khác đúng cho đủ điểm theo từng phần. ____HẾT____