SỞ GIÁO DỤC & ĐÀO TẠO TPHCM KIỂM TRA HỌC KÌ
TRƯỜNG THCS & THPT TRÍ ĐỨC
HỌC KÌ 2 - NĂM HỌC 2019-2020 MÔN: TOÁN - KHỐI 11
Thời gian làm bài: 90 phút;
(Học sinh không được sử dụng tài liệu)
Họ và tên học sinh: .......................................................................... Lớp: .............................
Bài 1(1,5 điểm). Tính giới hạn của các hàm số sau: 2 x  9 x  2 x  3  2 a) lim . b) lim . c) lim . x3 x  3 x x  3 x 1  x 1 2x  a khi x  1 
Bài 2 (1,0 điểm). Tìm tham số a để hàm số f  x 3 2   x  x  2x  2 liên tục tại x  1. khi x  1  x 1
Bài 3 (1,5 điểm). Tính đạo hàm các hàm số sau: 2 x  x a) 4 2 y  x  x 9 . b) y  . c) 3 y (x  4x  5)sin 4x . x 1 Bài 4 (1,5 điểm). a) Cho hàm số 3 2
y  x 2x 3 có đồ thị C. Viết phương trình tiếp tuyến của đồ thị C tại
điểm có hoành độ x  2 . 0 2x 1
b) Viết phương trình tiếp tuyến của đồ thị hàm số y 
biết tiếp tuyến song song với đường x 1
thẳng  :3x  y 11  0 . Bài 5 (3,5 điểm).
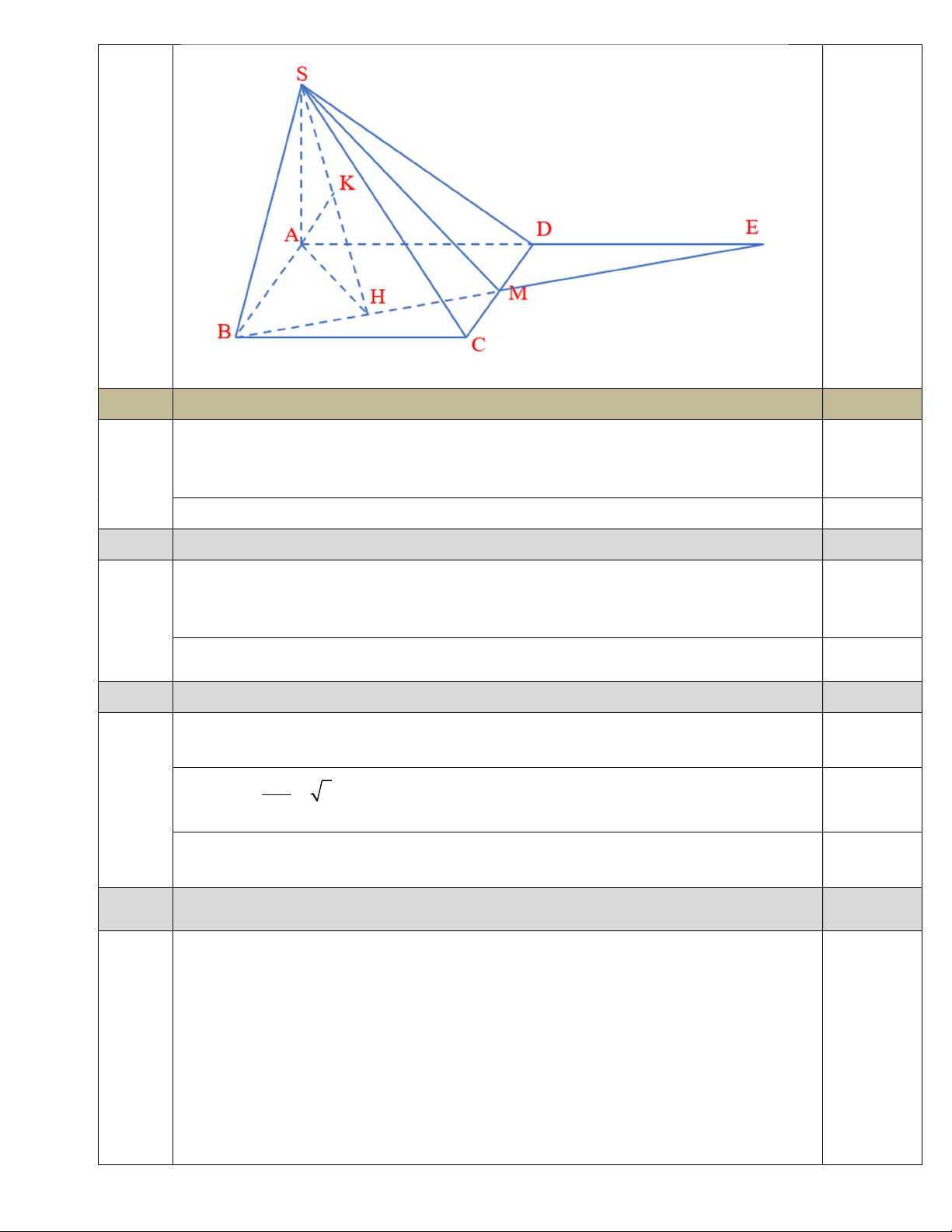
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, cạnh SA  2a 6 và SA   ABCD .
a) Chứng minh đường thẳng BC vuông góc mặt phẳng SAB .
b) Chứng minh mặt phẳng SAD vuông góc với mặt phẳng SCD .
c) Tính góc giữa đường thẳng SC và mặt phẳng  ABCD .
d) Gọi M là trung điểm CD . Tính khoảng cách từ D đến mặt phẳng SBM  . Bài 6. (1,0 điểm) 1 a) Cho hàm số f  x 3  x  m   2 2 3
1 x  m x  m 1. Tìm tất cả giá trị tham số m để 3 f  x  0, x   . 
b) Cho hàm số y  f  x có đạo hàm y  f  x liên tục trên  và hàm số y  g  x  f  3
4  x . Biết rằng tập tất cả các giá trị của x để f x  0 là  4  ;  3 . Tìm tập các
giá trị của x để g x  0 . ----------- HẾT ----------
SỞ GIÁO DỤC & ĐÀO TẠO TPHCM KIỂM TRA HỌC KÌ
TRƯỜNG THCS & THPT TRÍ ĐỨC
HỌC KÌ 2 - NĂM HỌC 2019-2020 MÔN: TOÁN - KHỐI 11
(Hướng dẫn chấm có 5 trang) HƯỚNG DẪN CHẤM CÂU NỘI DUNG ĐÁP ÁN ĐỀ 1 ĐIỂM 2 x  9 1.a lim 0,5 đ x3 x  3 2 x  9 x 3x  3 lim  lim  lim  x  3 0,25 x3 x  3 x3 x  3 x3 6. 0,25 x  2 1.b lim 0,5đ x x  3  2  2 x 1 x  2   1 0,25 lim  x lim    lim x x x  3 x  3 x  3 x 1 1    x  x  1 . 0,25 x  3  2 1.c lim 0,5 đ x 1  x 1 x  3  2
 x3 2 x32 x  3  4 0,25 Ta có lim  lim  lim x 1  x 1 x 1  x   1  x  3  2 x 1   x   1  x  3  2 1 1 1  lim   . 0,25 x 1   x  3  2 1 3  2 4 2x  a khi x  1  2
Tìm tham số a để hàm số f  x 3 2   x  x  2x  2 liên tục tại x  1. 0,5 đ khi x  1  x 1 * f   1  2  a . 0,25
* lim f x  lim 2x  a  2  a . 0,25 x 1 x 1   x  x  2x  2 x  1 2 3 2 x  2 * lim f  x  lim  lim  lim   . 0,25      2 x 2 3 x 1  x 1   x 1   x 1 x 1 x 1 
Hàm số f  x liên tục tại x 1  a  2  3  a 1. 0,25 3a 4 2 y  x  x 9 0,5đ 3 y  4 x  2 x 0,25*2 2 x  x 3b y  0,5 đ x 1 2 2 2
(x  x ) '(x 1)  (x  x )(x 1) '
(1 2x)(x 1)  (x  x ).1 0,25 y '   2 2 (x 1) (x 1) 2 x  2x 1  . 0,25 2 (x 1) 3c 3 y (x  4x  5)sin 4x 3 3
y ' (x  4x  5)'sin 4x  (x  4x  5)(sin 4x) 0,25 2 3
 (3x  4)sin 4x  4(x  4x  5)cos 4x 0,25 Cho hàm số 3 2
y  x 2x 3 có đồ thị C. Viết phương trình tiếp tuyến của đồ thị 4a 
C tai điểm có hoành độ x  2 . 0 + 2 y  3x  4x 0,25 Ta có: x  2 y  3 o o 0,25 y '(2)  4 0,25
Phương trình tiếp tuyến của đồ thị (C) tại M 2;3 :       y 4(x 2) 3 y 4x 5 0,25 2x  1
Viết phương trình tiếp tuyến của đồ thị hàm số y 
biết tiếp tuyến song song 4b x 1 0,5đ
với đường thẳng 3x  y  11  0 . D   \  1 3  y  x 2 1
Gọi M  x ; y là tiếp điểm của tiếp tuyến. 0 0  0,25 Theo giả thiết ta có    f  x  3 x 0  3   3  x 1  1  . 2  0 2 0 0   x   1 x  2  0 0 Với x  0  y  1
 : Phương trình tiếp tuyến: y  3x  0 1  y  3x 1 (N) 0 0 0,25
Với x  2  y  5: Phương trình tiếp tuyến: y  3 x  2  5  y  3x 11 (L) 0 0
Cho hình chóp S.ABCD có SA   ABCD , ABCD là hình vuông cạnh 2a, 5 SA  2a 6 . 5a
Chứng minh: BC  SAB 1đ
BC  AB (vì A B C D là hình vuông).
BC  SA (vì SA   ABCD ) 0,75  BC  SAB 0,25 b
Chứng minh: SCD  SAD 1đ
C D  A D (vì A B C D là hình vuông).
CD  SA (vì SA   ABCD ) 0,75
 CD  SAD  SCD  SAD 0,25
c) Tính góc giữa đường thẳng SC và mặt phẳng  ABCD . 1đ SC, ABCD      SC, AC    SCA 0,5 SA tan  SCA   3 AC 0,25  
SCA  60  SC, ABCD    0,25 5d
Gọi M là trung điểm CD. Tính khoảng cách từ D đến mặt phẳng SBM  0,5đ Gọi E  AD  BM
Dựng AH  BM H  BM  , AK  SH K  SH  . BM  SA  BM  AM 0,25  BM  SAH 
 BM  AK mà SH  AK  AK  SBM   d  , A SBM   AK 1 1 1 1 1 1 1 1 1 17          2 2 2 2 2 2 AK SA AH SA AB AE  2 2a2 4 2 6 a a 2 2 48a 4 51  AK  a 17 d D SBM  1  d  A SBM  1 2 51 , ,  AK  a 0,25 2 2 17 1 Cho hàm số f  x 3  x  m   2 2 3
1 x  m x  m 1. Tìm tất cả giá trị m để 6a 3 0,5đ
f  x  0, x  .  Ta có: f  x 2  x  m   2 2 1 x  m 0,25
f  x  0, x       0 f 0,25  m  2 1 2
1  m  0  2m 1  0  m  . 2
Cho hàm số y  f  x có đạo hàm y  f  x liên tục trên  và hàm số y  g x 6b với g  x  f  3
4  x . Biết rằng tập các giá trị của x để f x  0 là  4  ; 3. Tìm 0,5đ
tập các giá trị của x để g x  0 . g  x 2   x f  3 ' 3 . ' 4  x . 0,25 x  0  Ta có: g x  0 2   x f  3 3 . ' 4  x   0 2  x f  3 . ' 4  x   0   3 f '  4  x   0 0,25 x  0 x  0 x  0 x  0         1 x  2. 3 4  4  x  3 3 8  x  1 3 1   x  8 1   x  2 .
- Giám khảo vui lòng kiểm tra kỹ lại đáp án trước khi chấm.
- Học sinh giải các khác đúng vẫn cho đủ điểm. Chú ý: Câu 1:
- Ở 0,25đ đầu tiên các ý câu 1a, 1b, 1c nếu HS chỉ làm 1 trong 2 ý sau dấu bằng vẫn cho đủ 0,25đ.
- HS không làm mất dạng vô định (từ 1 đến 2 câu nhỏ) trước khi ra kết quả thì trừ 0,25đ trên toàn
bộ điểm bài 1, HS không làm mất dạng vô định cả 3 câu nhỏ trước khi ra kết quả thì trừ 0,5đ trên toàn bộ điểm bài 1. Câu 2:
- HS không làm mất dạng vô định trừ 0,25đ . Câu 3:
- Câu 3a, HS đúng được 1 trong 2 ý cho 0,25đ.
- Câu 3b, Ở 0,25đ đầu tiên HS chỉ làm 1 trong 2 ý sau dấu bằng vẫn cho đủ 0,25đ. Câu 5:
- Ở khung 0,75đ, mỗi ý vuông góc đúng là 0,25đ, HS có giải thích là 0,25đ.