SỞ GD&ĐT TP HỒ CHÍ MINH ĐỀ KIỂM TRA HỌC KÌ II
TRƯỜNG THPT AN DƯƠNG VƯƠNG Môn Toán - Khối 11- Năm học: 2019 -2020 Thời gian: 90 phút ĐỀ CHÍNH THỨC
Câu 1: (1,5đ) Tính các giới hạn sau: 3 3n  7 4x 1  3 a) (0,75đ) A  lim b) (0,75đ) B  lim 3 2n  4n  9 2 x2 x  4  x  3  2  , khi x  1 3  x 1 
Câu 2: (1đ) Cho hàm số: f x 1  
, khi x  1 . Xét tính liên tục của hàm số tại điểm x  1. 2 0 2x 10  1  , khi x  1 12  Câu 3: (1,5 đ)
a) (0,75đ) Tính đạo hàm của hàm số: sin 2x y  . 4 x 1 1 b)(0,75đ) Cho hàm số: 3 y  x  m   2
1 x  6m  22 x  5. Tìm tất cả giá trị của tham số m để 3 phương trình: /
y  0 có 2 nghiệm phân biệt. Câu 4: (1,5đ)
a) (0,75đ) Chứng minh rằng phương trình: 7 2
x  5x  2  0 có nghiệm. b) (0,75đ) Cho hàm số: 3 2
y  x  5x  4 có đồ thị (C). Lập phương trình tiếp tuyến d với đồ thị (C) tại
giao điểm của (C) với trục Oy.
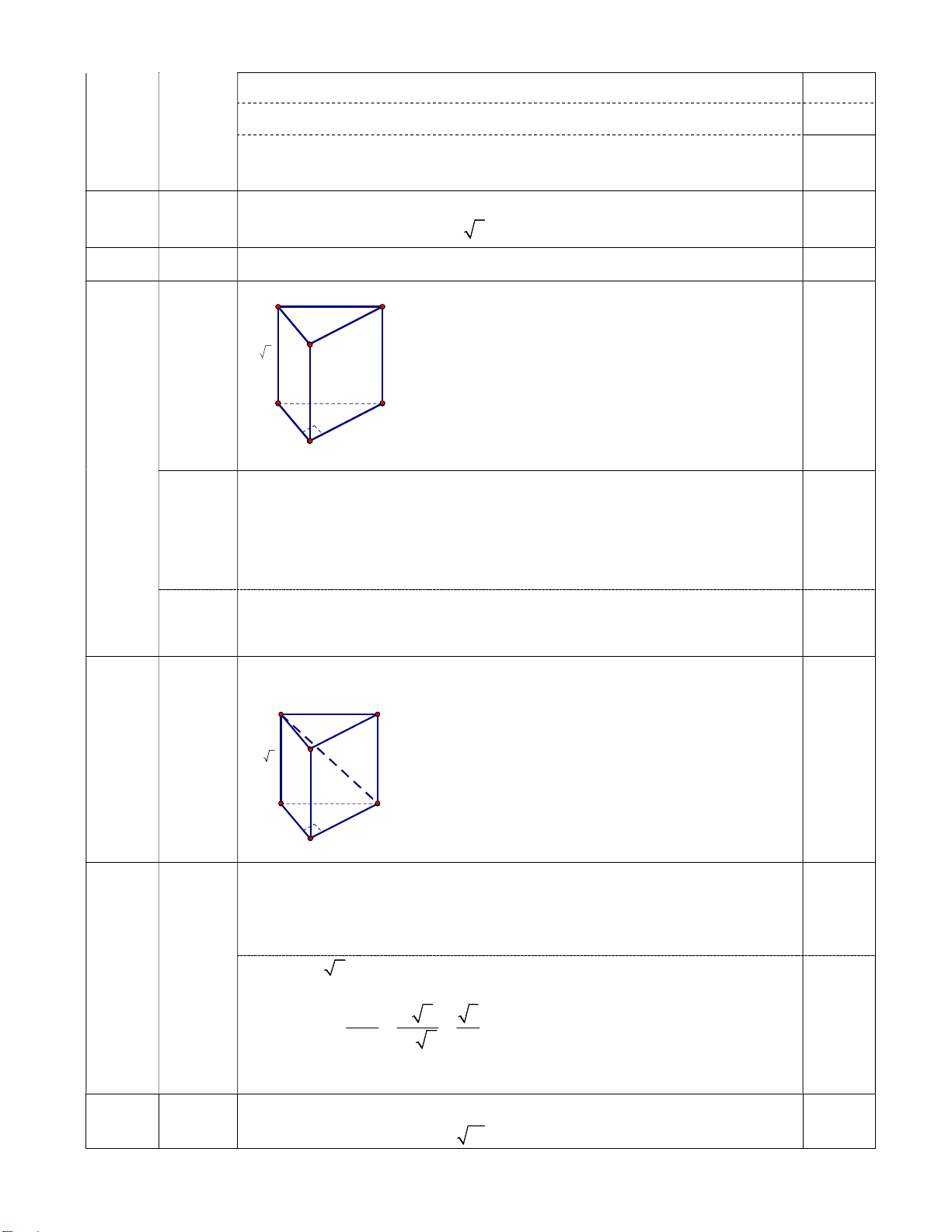
Câu 5: (1đ) Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC vuông cân tại B. Biết rằng AB  3a; AA'  a 6
a) (0,5đ) Chứng minh:  ABB ' A'  BCC ' B ' .
b) (0,5đ) Tính góc giữa đường thẳng A’C và mặt phẳng (ABC).
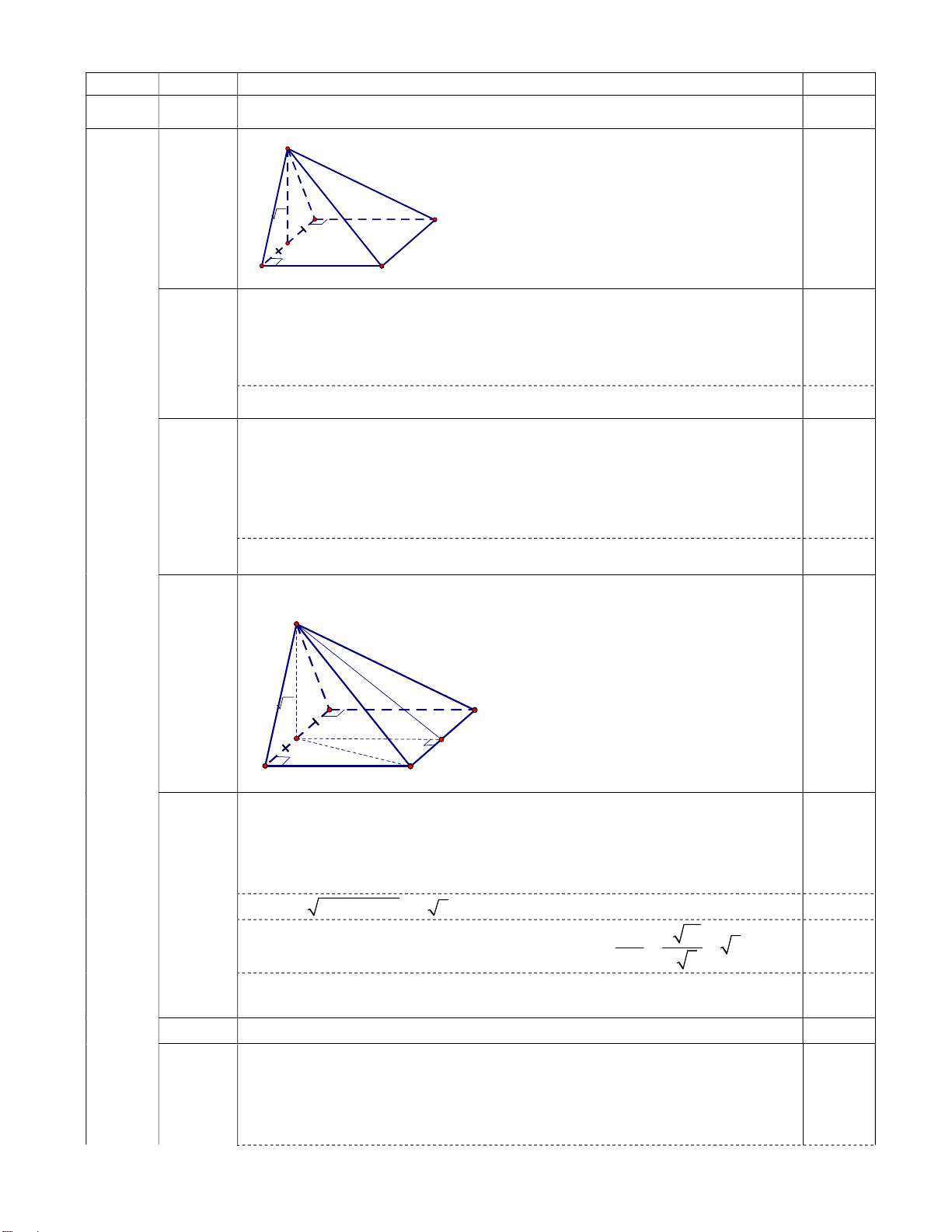
Câu 6: (3đ) Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh 2 . a H là trung điểm AB và
SH  a 15. Biết rằng hai mặt phẳng (SCH) và (SHD) cùng vuông góc với mặt phẳng (ABCD).
a) (1đ) Chứng minh: SH   ABCD và AD  SAB.
b) (1đ) Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
c) (0,5đ) Tính góc giữa mặt phẳng (SCD) và mặt phẳng (ABCD).
d) (0,5đ) Gọi I là trung điểm cạnh SD. Tính khoảng cách giữa IC và AD.
Câu 7: (0,5đ) Tính giới hạn của dãy số u biết: n  1 1 1 u    ... . n 2 1 1. 2 3 2  2 3 (n 1) n  n n 1 HẾT
SỞ GD&ĐT TP HỒ CHÍ MINH
TRƯỜNG THPT AN DƯƠNG VƯƠNG
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ II
MÔN TOÁN KHỐI 11 (NH: 2019 – 2020) Câu Ý Đáp Án Điểm 1 Tính các giới hạn sau: (1,5đ) a) 3 3n  7 (0,75 đ) A  lim 3 2n  4n  9 3  7  7 n 3  3  3  3 lim  n    lim n 0,25*2 3  4 9  4 9 n 2    2   2 3   2 3 n n  n n 3  0 3   . 0,25 2  0  0 2 b) 4x 1  3 (0,75 đ) B  lim 2 x2 x  4 4x 1  3   4x 8 lim  lim 0,25*2
x2  x  2  x  2
x2  x  2 x  2 4x 1  3 4 1  0,25 lim 
x2  x  2 4x 1  3 6 2  x  3  2 (1đ)  , khi x  1 3  x 1  Cho hàm số: f x 1   , khi x  1 . 2 2x 10  1  , khi x  1 12 
Xét tính liên tục của hàm số tại điểm x  1. 0 * f   1 1  ; 12  1  1 0,25 * lim f (x)  lim    .   2 x 1  x 1   2x 10  12 x  3  2 x 1 0,25 * lim f (x)  lim  lim   3 x x x 1 x      x   1  2 1 1 1 x  x   1  x  3  2 1 1 0,25  lim  x    . 2 1
x  x   x    12 1 3 2 1 0,25
Ta có: lim f (x)  lim f (x)  f (1) 
nên hàm số f(x)liên tục tại x 1 x 1   12 điểm x0 = 1. 3 (1,5 đ) a) sin 2x
Tính đạo hàm của hàm số: y  . (0,75 đ) 4 x 1
sin 2x/ . 4x  1sin 2x. 4x  / 1 0,25 Ta có: y '   x  2 4 1 2 4 x   3 1 cos2x  4x .sin 2x 0,25*2   x  2 4 1 b) 1 Cho hàm số: 3 y  x  m   2
1 x  6m  22 x  5. Tìm tất cả giá trị của (0,75đ) 3
tham số m để phương trình: /
y  0 có 2 nghiệm phân biệt. 2 y '  x  2m   1 x  6m  22. 0,25 a  0 Phương trình: /
y  0 có 2 nghiệm phân biệt   /   0  1   0 (Hien nhien) 0,25   2 m  4m  21  0  m  3  m  3 0,25   . Vậy 
thì thỏa yêu cầu bài toán. m  7 m  7 4 (1,5đ) a)
Chứng minh rằng phương trình: 7 2
x  5x  2  0 có nghiệm. (0,75 đ) Đặt f(x) = 7 2
x  5x  2 .Vì f(x) là hàm đa thức nên f(x) liên tục trên  0,25
=> f(x) liên tục trên đoạn [0; 2] (1)  f (0)  2 0,25 Ta có: 
 f (0). f (2)  212  0 (2)  f (2)  106
Từ (1) và (2), suy ra phương trình f x  0 có ít nhất 1 nghiệm trong 0,25
khoảng (0;2). Vậy phương trình f x  0 có nghiệm. b) Cho hàm số: 3 2
y  x  5x  4 có đồ thị (C). Lập phương trình tiếp tuyến
(0,75đ) d với đồ thị (C) tại giao điểm của (C) với trục Oy.
Gọi tiếp điểm là M (x , y ) . 0 0 0,25
Vì M Oy nên x  0 . Ta có: x  0  y  4 0 0 0 2
y'  3x 10x  y '(x )  y '(0)  0. 0,25 0
Vậy tiếp tuyến d tại điểm M (0; 4) có phương trình: 0,25
y  4  0.(x  0)  y  4. 5
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC vuông cân tại (1 đ)
B. Biết rằng AB  3a; AA'  a 6
a) 0,5 đ Chứng minh:  ABB ' A'  BCC ' B ' . Hình vẽ A' C' a 6 B' A C 3a 3a B
BC  AB (Do  ABC vuong tai B)  
BC  AA' (Do AA'   ABC   BC) Ta có:  BC  ABB' ' A . AB; AA'  ABB ' A' 0,25  AB AA' A     BC   ABB' A'  0,25 Vì:
   ABB' A'  BCC ' B' BC  BCC B  . ' ' 
b) 0,5 đ Tính góc giữa đường thẳng A’C và mặt phẳng (ABC). A' C' a 6 B' A C 3a 3a B
Ta có: A'C  (ABC)  C và A' A   ABCtại A
 CA là hình chiếu vuông góc của A’C lên mặt phẳng (ABC). 0,25  A'C; ABC        A'C;CA   A'C . A + AC  3a 2 . 0,25
Xét tam giác A’CA vuông tại A ta có: +  A' A a 6 3 tan A'CA      0 A'CA  30 . AC 3a 2 3 Vậy: A C  ABC  0 ' ;   30   . 6
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh 2 . a H là (3 đ)
trung điểm AB và SH  a 15. Biết rằng hai mặt phẳng (SCH) và
(SHD) cùng vuông góc với mặt phẳng (ABCD). a) 1đ
Chứng minh: SH   ABCD và AD  SAB. Hình vẽ S a 15 A D H 2a B 2a C SCH  ABCD  
Ta có: SHD   ABCD  0,25  
SCH  SHD  SH   SH   ABCD. 0,25 AD  AB (gt)  0,25 
AD  SH (Do SH   ABCD  AD) Ta có:  A ; B SH  SAB  AB SH H      ADSA  B . 0,25
b) 1 đ Tính góc giữa đường thẳng SC và mặt phẳng (ABCD). S a 15 A D H M 2a B 2a C
Ta có: SC  (ABCD)  C và SH   ABCDtại H
 CH là hình chiếu vuông góc của SC lên mặt phẳng (ABCD). SC;ABCD       SC;CH    SCH. 0,25 + 2 2 H C  H B  B C  a 5 . 0,25 0,25
Xét tam giác SCH vuông tại H ta có:  SH a 15 tan SCH    3. CH a 5   0
SCH  60 . Vậy: SC  ABCD  ;  0    60 . 0,25
c) 0,5 đ Tính góc giữa mặt phẳng (SCD) và mặt phẳng (ABCD). Gọi M là trung điểm CD. Ta có: SCDABCD  CD   Trong  ABCD / \
co HM  CD tai M (Do BCMH la hcn)   Trong SCD /
co SM  CD tai M (Do CD  SH,CD  MH  SCD; ABCD       SM;MH    SMH. 0,25
Xét tam giác SMH vuông tại H ta có: SH a +  15 15 tan SMH    . MH 2a 2 0,25   0
SMH  62 41'. Vậy: SCD  ABCD  ;  0    62 41'.
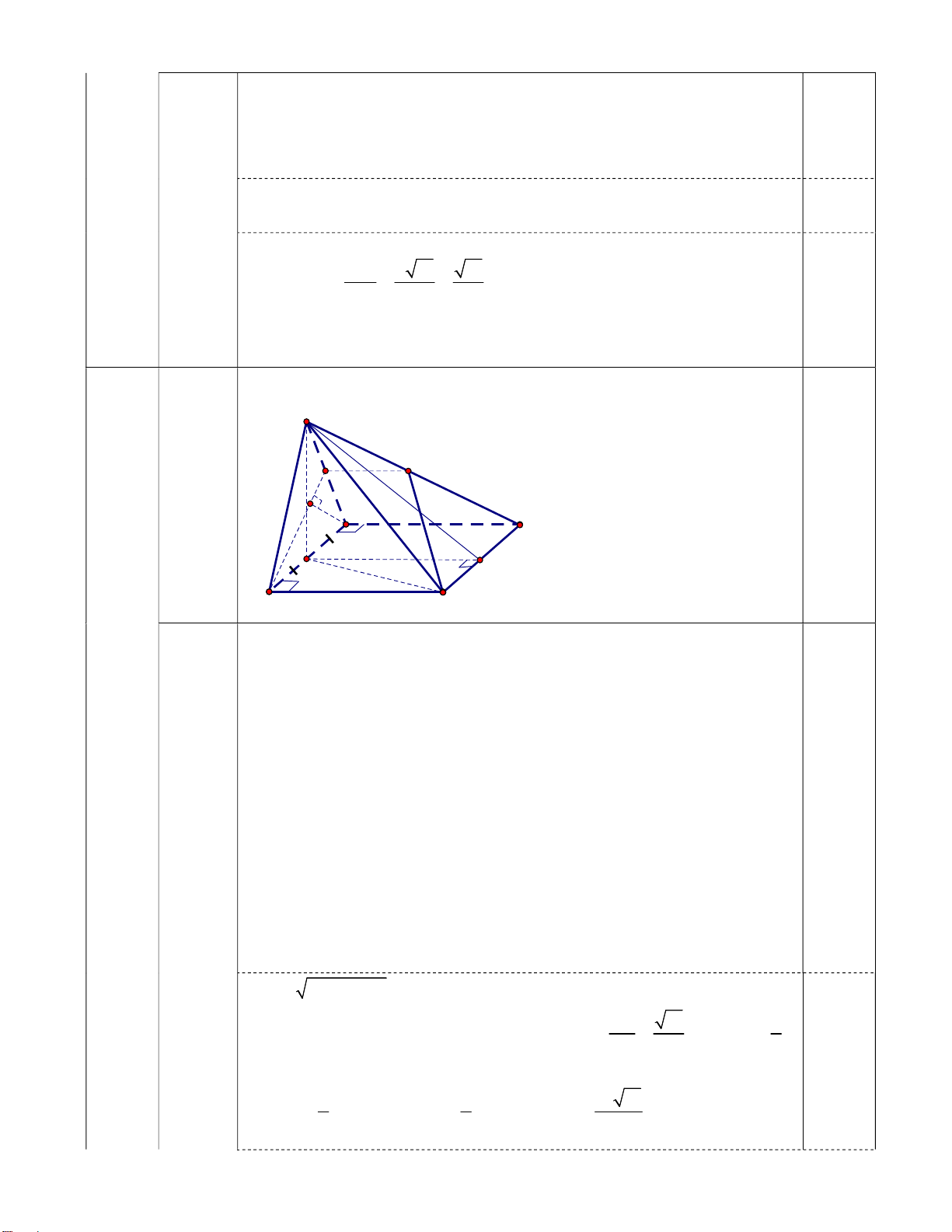
d) 0,5 đ Gọi I là trung điểm cạnh SD. Tính khoảng cách giữa IC và AD. S I E A K D H M 2a B 2a C AD / /BC  
Ta có: AD  (IBC)  AD / /(IBC) BC (IBC)    d(A ;
D IC)  d (AD;(IBC))  d ( ; A (IBC)).
Gọi E là trung điểm SA. Ta có: IE / /BC (Cùng // với AD)  IE  IBC Kẻ AK  BE tại K. AK  BE  
AK  BC (Do BC / / AD  BC  SAB  AK ) 0,25 Ta có:  BE; BC  IBC   BE BC B    
 AK IBC tại K d( ; A (IB ) C )  AK. + 2 2 SA  SH  HA  4 . a
Xét tam giác SHA vuông tại H, ta có:  SH 15 SAH    1 sin ;cos SAH  . SA 4 4 Xét tam giác ABE, ta có: + S  AB AE  EAB  a a  2 1 1 a 15 . .sin 2 .2 .sin SAH  . A  BE 2 2 2 + 2 2 2 BE  AB  AE  ABAE  2 2 EAB  a  a  a a  2 2 .cos 4 4 2.2 .2 .cos SAH  6a .  BE  a 6. 0,25 1 2S a 10 Mặt khác: S  AK. A  BE BE  AK   . A  BE 2 BE 2 a 10 Vậy: d(AD; IC)  . 2 7
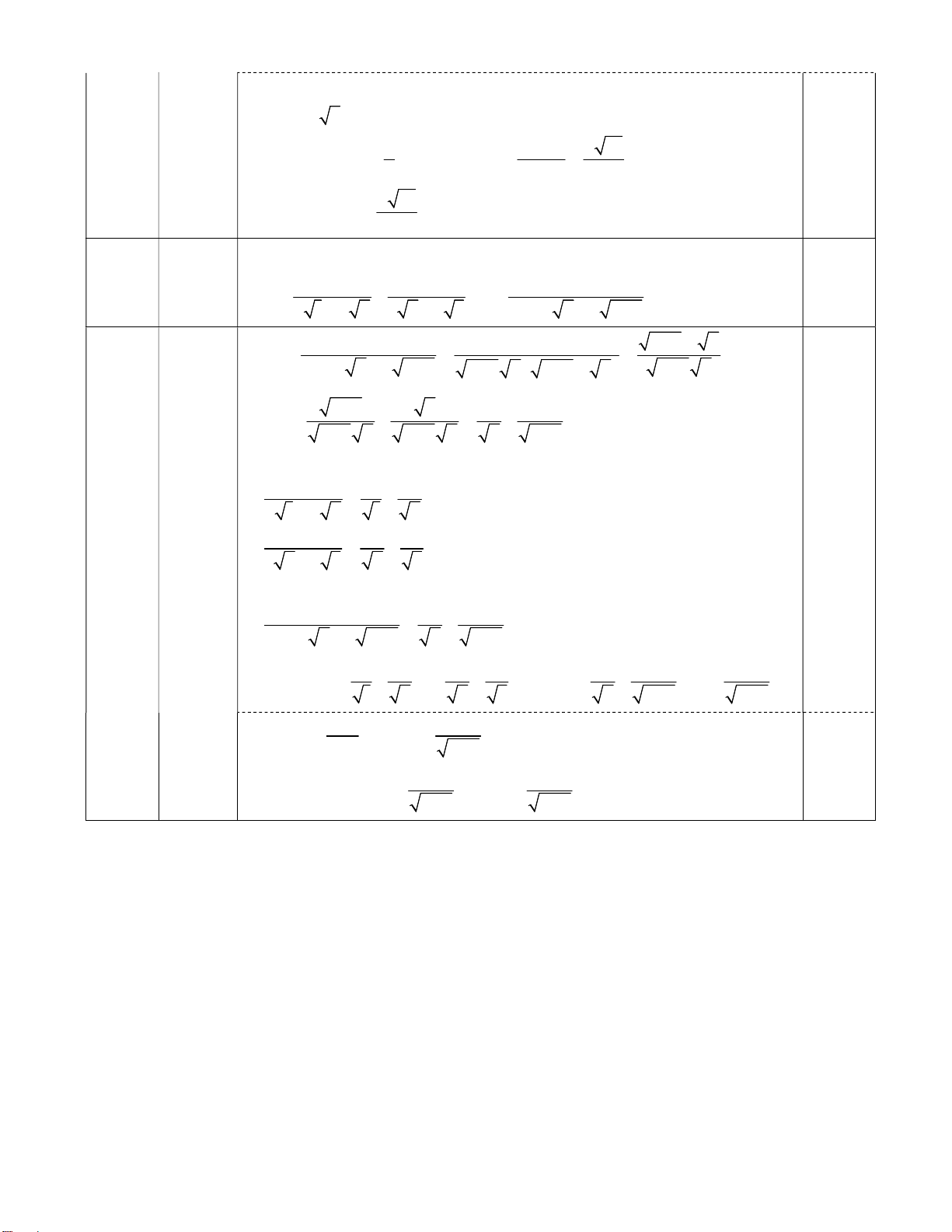
Tính giới hạn của dãy số u biết: n  (0,5đ) 1 1 1 u    ... . n 2 1 1. 2 3 2  2 3 (n 1) n  n n 1   Ta có: 1 1 n 1 n   (n 1) n  n n 1 n 1 n  n 1  n  n 1 n n 1 n 1 1     n 1 n n 1 n n n 1 Tức là: 1 1 1     2 1 1. 2 1 2    1 1 1      3 2  2 3 2 3  0,25
.....................................   1 1 1     (n 1) n n n 1 n n 1             Suy ra: u  1 1 1 1 1 1 1     ........   1 n        1 2   2 3   n n 1  n 1 1 1 Ta có: lim  0  lim  0 n 1 n 1  1  1 0,25 Vậy: lim u  lim 1  1 lim 1. n    n 1  n 1