SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ II THÀNH PHỐ HỒ CHÍ MINH
MÔN TOÁN HỌC – LỚP 11 - (20.06.2020) TRƯỜNG THPT BÀ ĐIỂM
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ tên học sinh: ………………..…………….…………, Lớp: ………, Số báo danh: …………….......
Câu 1 (2 điểm): Tính giới hạn hàm số 3 x  27 2 4x  5  2x 1 a) lim b) lim  2 x 3 x  5x  6 x x  2 x  3x  1 Câu 2 (1 điểm): 2  x  3x  2  khi x  1 Cho hàm số f (x)   x 1
. Tìm tất cả các giá trị m để hàm số liên tục tại x0 =1 2mx 5 khi x  1  
Câu 3 (1 điểm): Tính đạo hàm của các hàm số sau 2 x a) 6 y  x  4 x   2 2 2 b) 2 y  tan(x  2)  sin x x
Câu 4 (1 điểm): Viết phương trình tiếp tuyến của đồ thị (C) : y 
biết tiếp tuyến song song 2x  3
đường thẳng  : y  3x  2 .
Câu 5 (1điểm): Cho hàm số 3
y  x  3x 1 có đồ thị (C). Viết phương trình tiếp tuyến của C tại giao
điểm của (C) và trục Oy
Câu 6 (2 điểm): Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a ,  BAD  60, SA  4a và SA  (ABCD)
a) Chứng minh BD  SAC .
b) Xác định và tính góc giữa (SCD) và (ABCD)
Câu 7 (2 điểm): Cho hình lập phương ABC . D A B  C  D   có cạnh bằng 1.
a) Chứng minh: AD '   A' B ' D
b) Khoảng cách từ điểm A đến mặt phẳng  ABD HẾT
ĐÁP ÁN VÀ THANG ĐIỂM MÔN TOÁN 11 CÂU ĐÁP ÁN ĐIỂM 1
Câu 1 (2 điểm): Tính giới hạn hàm số 3 (2.0đ) x  27 a) lim  2 x 3 x  5x  6 x3 2x 3x9  lim 0.5 x3 x3x2 2 x  3x  9  lim 0.25 x3 x  2  27 0.25 2 4x  5  2x 1 b) lim x x  2 x  3x  1 4x 5 2x 2 2     2 1 x x 3x 1          lim 0.5 x  2 x  2 x  3x 1 2 4x  5  2x  1  4    3 1
4x  4x 2x 3x  4  1 1     1    2   x x x lim x =   lim 0.25 x 3x 1 2 4x  5  2x  1 x  1   3  5 1   4   2      x  x x  2 0.25 =  3 2 2  x  3x  2  khi x  1
(1.0đ) Câu 2: Cho hàm số f (x)   x 1 . 2mx 5 khi x  1  
Tìm tất cả các giá trị m để hàm số liên tục tại x0 = –1 f(–1) = – 2m  5 0.25
lim f (x)  lim 2mx  5       2m 5 x 1  x1 0.25 2 x  3x  2 x  1x  2 lim f (x)  lim  lim  lim x  2 = 1 0.25 x 1  x 1  x 1 x 1  x 1 x 1   
Hàm số f(x) liên tục tại x0 = –1  lim f (x)  lim f (x)  f(–1)  2m  5 = 1  m = 2 0.25 x 1  x 1  3.
Câu 3: Tình đạo hàm của các hàm số sau (1.0đ) 2 x a) 6 y  x  4 x   2 2 2 5 2 1  0.5 y '  3 2x   x 2 b) 2 y  tan(x  2)  sin x  y  x   2 ' (
2) ' 1 tan (x  2)  2sin x(sin x)' 0.25 2
 1 tan (x  2)  2sin x cos x 0.25 4. x
Câu 4: Viết PT tiếp tuyến của đồ thị (C) : y 
biết tiếp tuyến song song đường thẳng (1.0đ) 2x  3  : y  3x  2 .
Gọi M (x ; y ) là tiếp điểm 0 0 0 3 0.25 y '  2 (2x  3) y '(x )  3 0.25 0 3 x  1   y  1 0.25 0 0   3  2x  3  1   2 0  (2x  3) x  2   y  2 0  0 0
Vậy PT tiếp tuyến cần tìm là 0.25  y  3(x 1) 1  y  3x  2 (L)    y 3(x 2) 2      y  3x  8 (N) 5. Câu 5: Cho hàm số 3
y  x  3x 1 có đồ thị (C). Viết PT tiếp tuyến của C  tại giao điểm của (C) và (1.0đ) trục Oy
Gọi M  x , y là tiếp điểm 0 0  0.25 3
x  0  y  x  3x 1  1  0 0 0 0 / 2 y  3x  3 0.25 /  y x  3  0.25 0 
phương trình tiếp tuyến của (C) tại M 0 ;   1 là : / y  y  x x  x  y  3x 1 0.25 0   0  0 6
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a ,  BAD  60, SA  4a và (2.0đ) SA  (ABCD)
a) Chứng minh BD  SAC . Ta có
BD  AC (do ABCD là hình thoi) 0.75
 BD  SA SAABCD  S , A AC   SAC,SA AC  A  BD  SAC 0.25
b) Xác định và tính góc giữa (SCD) và (ABCD) Kẻ AH  CD tại H ,.  CD  SA 0.25 
 CD  SAH   CD  SH C  D  AH  (SCD)  (ABCD)  CD 0.25 
 Trong (SCD) :CD  SH   ((SCD),(ABCD))   (SH; AH ) T  rong (ABCD):CD  AH  0.25
Xét AHD vuông tại H , 
ADH  60 ta có AH  A . D sin 60 3  2a  a 3 2 Vậy  0 ((SCD),(ABCD))  66,6 0.25  SA 4a 3 tan SHA     0 SHA 66,6 AH 3     7
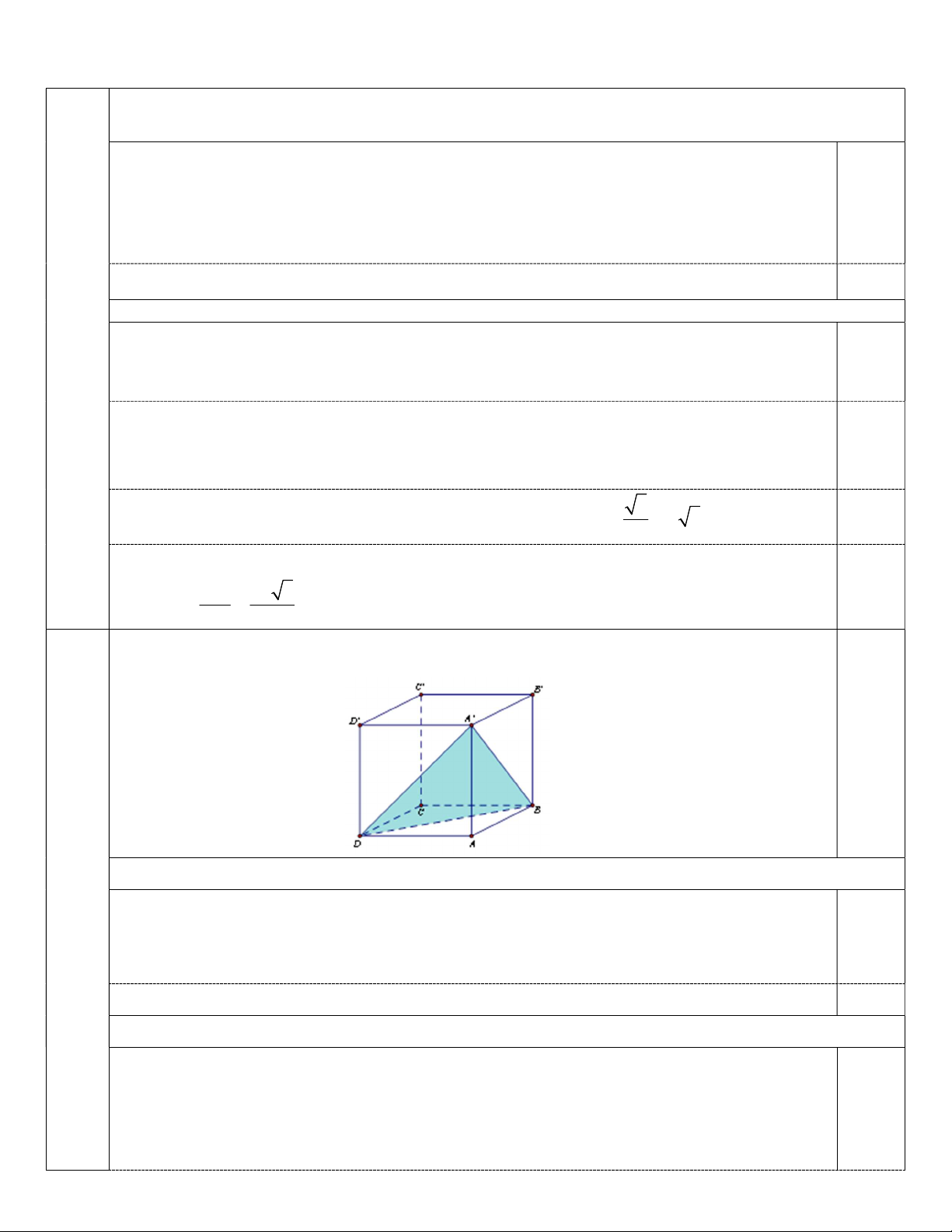
Câu 7. Cho hình lập phương ABC .
D A B C D có cạnh bằng 1. (2.0đ)
a/ Chứng minh: AD '   A' B ' D AD '  A' D  AD ’ D ’ A là hình vuông  0.75 
AD '  A' B ' (A' B '  (ADD ' A'))
Trong  ’A ’BD: ’AD ’A ’ B ’    A  AD '   A' B ' D 0.25
b) Khoảng cách từ điểm A đến mặt phẳng  ABD
Gọi O là tâm của hình vuông ABCD 0.5 Ta có: BD  AC   BD  (AA'C'C) BD  AA'
Từ A kẻ AK  A’O tại K
AK  BD ( BD(AA’C’C),)
Trong (A’BD): A’O  BD = K
 AK   A' BD tại K  d( ; A  A' B ' D)  AK 1 1 1    3 2 2 2 AK A' A AO . 3  AK  3 0.5 Vậy d A  A B D 3 ( ; ' ' )  AK  3