SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KỲ II THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2019- 2020 TRƯỜNG THPT BÁCH VIỆT Môn thi: Toán Khối 11 _________
Thời gian làm bài: 90 phút Đề thi chính thức
(không kể thời gian giao đề) Đề thi có 01 trang Ngày thi: 27 / 6 /2020
Câu 1: (2 điểm) Tìm các giới hạn sau. 3 2 6x  2x  3 2x  3x 1 4.5n  2 a. lim b. lim c. lim 3 x x  3x  2 x 1  x 1 3.2n  2.5n x  2 n 1 x.m 1  x 1 d. lim e. lim x 1  x 1 x0 x 2 3x  7x  2  , khi x  2 
Câu 2: ( 1 điểm) Cho hàm số f (x)   x  2  2  mx 1, khi x  2 
Tìm m để hàm số liên tục tại x  2
Câu 3: (2 điểm) Tính đạo hàm của các hàm số sau. 1000  a.  1 3 x 2 4  y  x  4 x   51   b. 2 5 y  cos( ) c. 4 3 y  5x  2x  cos 2x d. 10 y  sin  4 x  x 1 2 x
Câu 4: (1 điểm ) Cho hàm số 3 2
y  f (x)  x  6x  9x cos đồ thị (C)
a. Viết phương trình tiếp tuyến của (C) biết tiếp điểm có hoành độ bằng -2 b. Giải phương trình ' f (c osx)=0 
Câu 5: ( 0,5 điểm ) Cho hàm số 2x 2 y  có đồ thị (C) x 1
Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến vuông góc với đường thẳng y  x 1
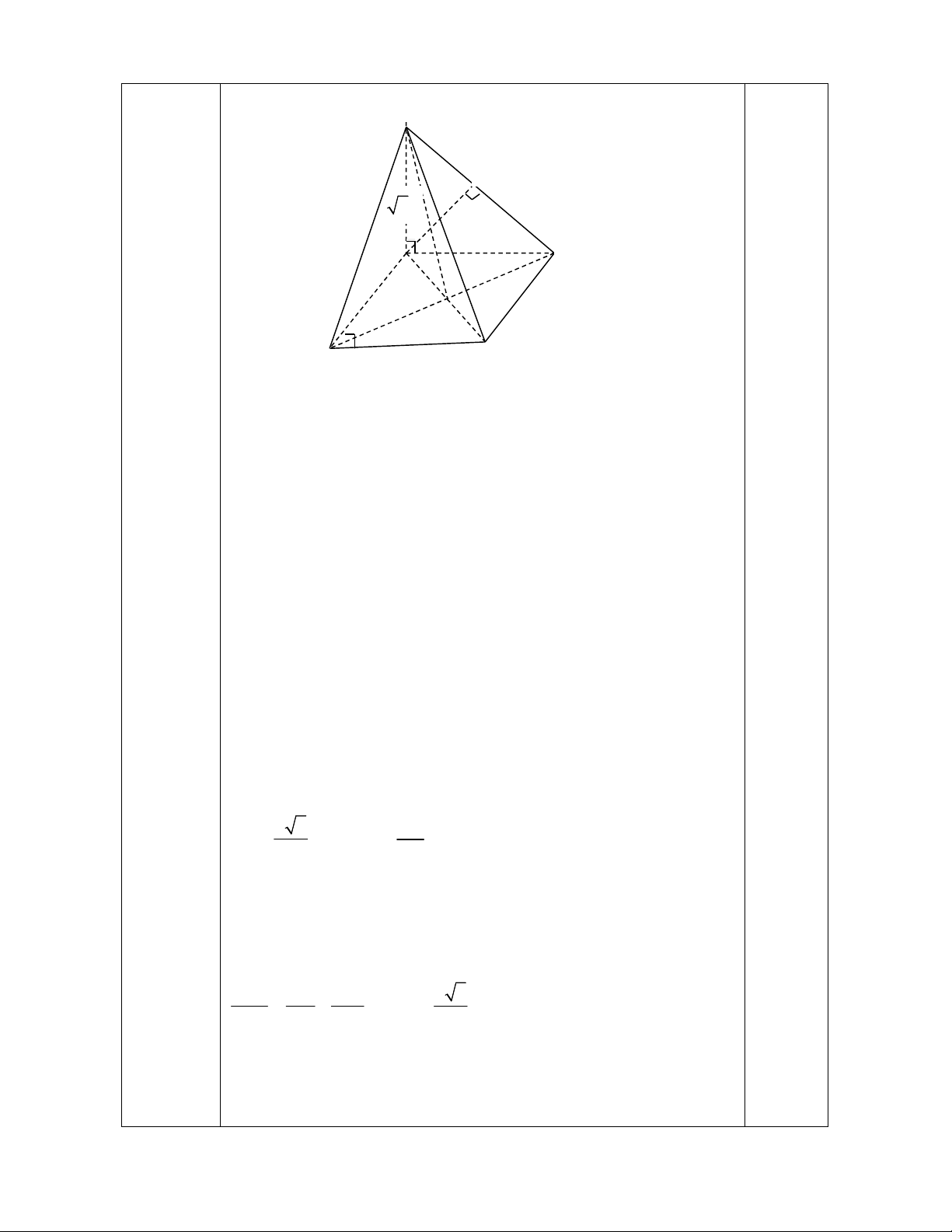
Câu 6: (2,5 điểm ) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA  (ABCD), SA= a 2
a.Chứng minh : BD  (SAC),(SAB)  (SAD)
b.Gọi H là hình chiếu vuông góc của A trên SB . Chứng minh BC  AH
c.Gọi O là giao điểm của hai đường chéo hình vuông. Tính góc giữa SO và (ABCD)
d.Tính khoảng cách giữa hai đường thẳng SB và AD
e. Tính khoảng cách từ O đến mặt phẳng ( SBD )
Câu 7.(0,5 điểm ) Chứng minh rằng phương trình 5 4
x  3x  5x  2  0 có ít nhất hai nghiệm thuộc khoảng (0;2). -----------HẾT------------- 
Thí sinh không được sử dụng tài liệu 
Giám thị không giải thích gì thêm
Họ và tên học sinh: ................................................ Số báo danh: ..................... ...................
Chữ ký của giám thị 1: .......................................... Chữ ký của giám thị 2 ..........................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM THI MÔN TOÁN THÀNH PHỐ HỒ CHÍ MINH
KIỂM TRA CUỐI HỌC KỲ II KHỐI 11 TRƯỜNG THPT BÁCH VIỆT NĂM HỌC 2019 – 2020 _________ ĐỀ THI CHÍNH THỨC
(Bản Hướng dẫn chấm thi gồm 04 trang) Câu Nội dung Điểm Câu 1: 3 2 3 x (6   ) 2,5 điểm 3 2 3 6x  2x  3 a. lim  lim x x  6 0,5 3 x x  3x  2 x 3 3 2 x (1  ) 2 3 x x KL: 2x  3x 1
(2x  3x 1).(2x  3x 1) . b lim  lim x 1  x 1 x 1     (x 1).(2x 3x 1) 0,5 (x 1)(4x 1) 5  lim  x 1  (x 1).(2x  3x 1) 4 KL: 5 n 2 n 4.( )  4.5  2 n c. 5 5 lim  lim  2  3.2n  2.5n 2 n 5 3.( )  2.( )n 5 5 0,5 KL: lim(x  2)  1  0 x 1   x  2 d. Ta có : 0,5  lim(x1)  0  lim   x 1   x 1  x 1  x 1  0, x   1  n 1 x. m 1  x 1
m 1  x.(n 1  x 1) m 1  x 1 e. lim  lim(  ) x0 x0 x x x n 1  n2
m 1  x.(n 1  x 1)).( n 1 n  x  1 x  .. n  1 x 1)  lim( n 1  n2 x0 . x (n 1 n  x  1 x  .. n  1 x 1) 0,5 n 1 
(m 1  x 1).(m 1  x ...1)    )   n 1  .(m 1  ...1) n m x x KL: Câu 2: 2 3x  7x  2 (3x1)(x 2) 1 điểm Ta có: lim  lim  5  x2 x 2 x  2  x  2 0,5 Mặt khác : f ( 2  )  4  m 1 3
Hàm số liên tục thì : 4m 1  5  m  0,5 2 KL: Câu 3: '  1 3 4 1000  2 điểm .
a y '  ( x  4 x   51)  4 x    0,5 1 3 2 3 4 999 3
 1000( x  4 x   51) .(x   ) 2 4 x x x KL: '     b. 2x 5 7 2x 5 y '  cos( )  sin( ) 0,5   2  x 1  (x 1) x 1 KL: 3 ' 10x  3x  sin 2x c. 4 3
y '  5x  2x  cos2x  4 3 5x  2x  o c s2x 0,5 KL: 2 2 2 10 9 d.y '  (sin ) '  10.sin (sin ) ' 2 2 2 x x x 4  0 2 4 9  .sin .sin 0,5 3 2 2 x x x KL Câu 4:
a. Gọi PTTT có dạng : y  y '(x ).(x x )  y(x ) 0 0 0 1 điểm Ta có: 2 y '  3  x 12x  9
Hoành độ tiếp điểm bằng -2  x  2 0 y(2)  50 y '(2)  45 0,5 PTTT: y  4
 5(x  2)  50  45x  40 KL: b. f '(cosx)=0 2
 cos x 12cos x  9  0  cos x  3(PTVN )    cos x  1 0,5
cos x  1  x  k 2 , k   KL Câu 5:
Gọi PTTT có dạng : y  y '(x ).(x x )  y(x ) 0 0 0 0,5 điểm 2x  2 4 Ta có : y '  ( ) '  2 x 1 (x 1)
Vì PTTT vuông góc với y=-x+1 nên ta có: 4 y '(x ).(1)  1  1(x  1) 0 2 0 (x 1) 0  x  1 2 0 (x 1)  4  0,25 0 x  3  0
Tại x  1: y '(1)  1; y(1)  0 0 PTTT: y  x 1 Tại x  3  : y '( 3  )  1; y( 3  )  4 0 PTTT: y  x  7 KL: 0,25 Câu 6: 2,5 điểm S H a 2 A B O C D a a.+) Cm: BD  (SAC) BD  AC 0,25 Ta có : 
( ABCD là hình vuông, SA là đường cao )  BD  SA  BD  (SAC)
+) cm : (SAB)  (SAD)  cm : AD  (SAB) 0,25  AD  SA Ta có: 
( ABCD là hình vuông, SA là đường cao ) AD  AB
 AD  (SAB) mà AD  (SAD)  (SAD)  (SAB)
b.cm : BC  AH  cm : BC  (SAB) 0,5  BC  SA Ta có:  BC  AB
 BC  (SAB) mà AH  (SAB)  BC  AH c. Góc giữa SO và (ABCD)
SA  (ABCD)  A là hình chiếu của S lên (ABCD) 0,5
 AO là hình chiếu của SO lên (ABCD)
Góc giữa SO và (ABCD) chính là góc giữa SO và AO ˆ  SOA a 2 SA AO  0 ˆ ˆ tan SOA   2  SOA  63 2 AO d.d(SB,AD) 0,5
Ta có: AD  BC  AD  (SBC)
 d(SB, AD)  d(AD, SBC)  d ( , A SBC)  AH Cm: AH  (SBC)(cmb)
Xét tam giác vuông SAB ta có: 1 1 1 a 6    AH  2 2 2 AH SA AB 3 e.d(O,SBD) O  BD BD  (SBD) 0,5  d(O,SBD)  O  0a Câu 7: Đặt 5 4
f (x)  x  3x  5x  2 thì f(x) liên tục trên R 0,5 điểm f (0)  2 Ta có: f (1)  1 0,5 f (2)  8  f (0). f (1)  2
  0 do đó có ít nhất một nghiệm thuộc (0;1)
f (1). f (2)  8  0 do đó có ít nhất một nghiệm thuộc (1,2)
Mà (0;1) và (1;2) là hai khoảng riêng biệt do đó phương trình đã
cho có ít nhất hai nghiệm thuộc (0,2) --- HẾT ---