SỞ GD - ĐT TP. HỒ CHÍ MINH ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2019 – 2020
Trường THPT Bình Hưng Hòa Môn: TOÁN; Lớp 11
Thời gian làm bài: 90 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC
(Đề kiểm tra có 01 trang) 2 3n  2n 1
Câu 1 (1,0 điểm). Tính giới hạn lim . 2 2n  n  4 x  x  2
Câu 2 (1,0 điểm). Tính giới hạn lim . 2 x2 x  4 3 2 2x  4x  x  2  khi x  2
Câu 3 (1,0 điểm). Cho hàm số 2 f (x)   x  x  2 . 2x1 khi x  2
Xét tính liên tục của hàm số tại điểm x  2. 0
Câu 4 (2,0 điểm). Tìm đạo hàm của các hàm số sau : 2 2x  x  3 a) 4 y  x  m   2 2
2 x  3m  7 (m là tham số). b) y  . x 1    c) 2 y  5x  3x 1. d) 2 y  cos 3x  .    4 
Câu 5 (1,0 điểm). Viết phương trình tiếp tuyến của đồ thị hàm số C y  f  x 3 2 :  x  3x  7x  3
biết hệ số góc của tiếp tuyến bằng 10 .
Câu 6 (2,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA
vuông góc với mặt đáy  ABCD và SD  a 5 . Gọi M là trung điểm của cạnh S . A
a) Chứng minh rằng mặt phẳng SCD vuông góc với mặt phẳng SAD.
b) Tính tang của góc giữa hai mặt phẳng MCD và  ABCD .
Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm O với AD  2AB  2 . a
Mặt bên SAD vuông góc với mặt đáy và SA  a 3, SD  .
a Gọi M là trung điểm của DO. Tính
khoảng cách từ điểm M đến mặt phẳng SBC. v
Câu 8 (1,0 điểm). Một vật chuyển động trong 2 giờ theo quy luật 3 2
s  at  bt với t (h) là khoảng thời gian tính từ lúc vật bắt đầu chuyển 4
động và s (km) là quãng đường vật đi được trong khoảng thời gian đó.
Biết rằng kể từ lúc bắt đầu chuyển động, sau 1,5 giờ vận tốc của vật có
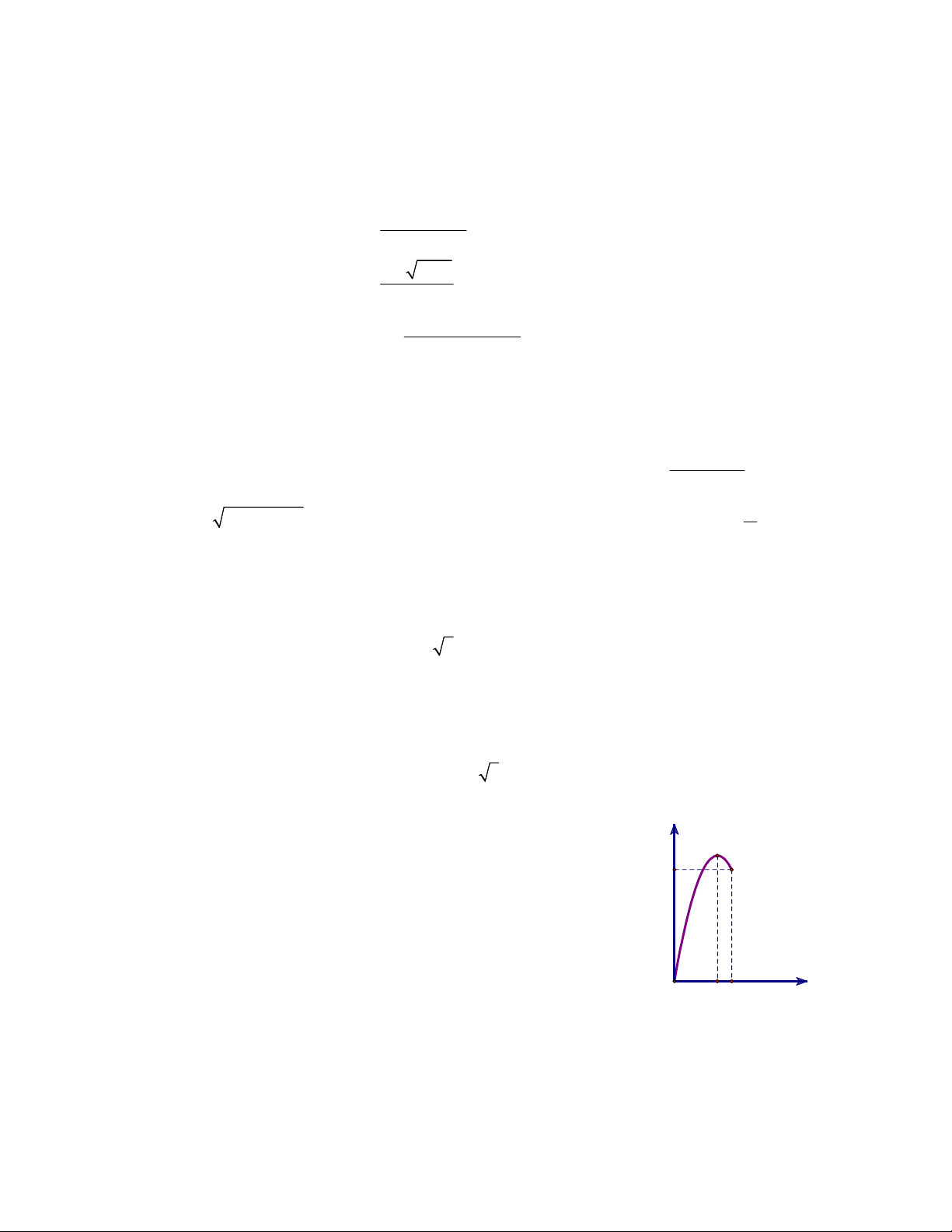
giá trị lớn nhất và sau 2 giờ vật có vận tốc bằng 4 (km/h). Đồ thị vận tốc
của vật được minh họa như hình vẽ bên. Tính quãng đường s mà vật di t
chuyển được trong 2 giờ đó. O 1,5 2 ………..HẾT……….
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:…………………………; Số báo danh:.………….;Lớp:……..
SỞ GD-ĐT TP. HỒ CHÍ MINH
ĐÁP ÁN KIỂM TRA HỌC KÌ II NĂM HỌC 2019-2020
Trường THPT Bình Hưng Hòa Môn: TOÁN; Lớp 11 Lưu ý Câu Đáp án Điểm khi chấm 2 3n  2n 1 Tính giới hạn: lim . 1 2 2n  n  4 2  2 1  n 3    2   n n lim    1 4 2  n 2    2  0,5 Câu 1  n n  (1,0 điểm) 2 1 3   2  lim n n 0,25 1 4 2   2 n n 3   . 0,25 2 x  x  2 Tính giới hạn: lim . 1 2 x2 x  4 2 x  x  2  lim 0,25 x2  2 x  4x  x  2 Câu 2 x  2x   1 (1,0  lim 0,25 x2 điểm)
x  2x  2x  x  2 x 1  lim x2  0,25 x  2x  x  2 3  . 0,25 16 3 2 2x  4x  x  2  khi x  2 Cho hàm số 2 f (x)   x  x  2 .  1 2x 1 khi x  2
Xét tính liên tục của hàm số tại điểm x  2. 0 Câu 3 f (2)  2.2 1  3. (1,0 0,25 điểm)    x  2 2 3 2 2x x x x   2 1 2 4 2 2x 1 lim f (x)  lim  lim  lim  3 0,25 2 x2 x2 x2 x  x  2 x  2x   x2 1 x 1 lim f (x)  f (2) 0,25 x2
Vậy hàm số f  x liên tục tại x  2. 0 0,25
Tính đạo hàm của các hàm số sau: a) 4 y  x  m   2 2
2 x  3m  7 (m là tham số). 1 3 Câu 4
y  4x  2m  2 . x 0,5 (2,0 2 2x  x  3 điểm) b) y  0,5 x 1  2 2x x 3 x  1  2 2x x 3x  1         y  0,25 x  2 1 2 2x  4x  2 y '  0,25 2 (x 1) c) 2 y  5x  3x 1. 0,5  2 5x 3x 1   y  0,25 2 2 5x  3x 1 10x  3 y  0,25 2 2 5x  3x 1    d) 2 y  cos 3x    0,5  4          y  2cos 3x  cos 3x      0,25  4   4           y  2cos 3x  sin 3x  3x        4   4  4  0,25       y  6  cos 3x  sin 3x  .      4   4 
Viết phương trình tiếp tuyến của đồ thị hàm số C  y  f  x 3 2 :
 x  3x  7x  3 biết hệ 1
số góc của tiếp tuyến bằng 10 . Câu 5 f  x 2
 3x  6x  7 , f (x )  10 . 0 0,25 (1,0 2  điểm)
f (x )  10  3x  6x  7  1  0  x  1  0 0 0 0 0,25 y  6 0 0,25
Phương trình tiếp tuyến  : y  10x  4 0,25
Cho hình chóp S.ABCD có đáy ABCD là hình vuông
cạnh a . Cạnh bên SA vuông góc với mặt đáy  ABCD
và SD  a 5 . Gọi M là trung điểm của cạnh S . A 2
a) Chứng minh rằng mặt phẳng SCD vuông góc với mặt phẳng SAD. 1
CD  AD (ABCD là hình vuông) 0,25
CD  SASA   ABCD 0,25 Câu 6  CD  SAD 0,25 (2,0 điểm)  SCD  SAD. 0,25
b) Tính tang của góc giữa hai mặt phẳng MCD và  ABCD . 1
MCD   ABCD  CD 
MD  CD, MD  MCD  0,25 AD  CD, AD    ABCD
 MCD, ABCD  MD, AD   MDA 2 2 SA  SD  AD  2a 0,25 MA  a 0,25 MA 0,25 tan  MDA   1 AD  
Câu 7 Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm O với AD 2AB 2 . a Mặt bên SAD (1,0
vuông góc với mặt đáy và SA  a 3, SD  .
a Gọi M là trung điểm của DO. Tính khoảng 1
điểm) cách từ điểm M đến mặt phẳng SBC.
Gọi H là hình chiếu của S trên cạnh AD. SAD   ABCD 
SAD   ABCD  AD  SH  AD, SH   SAD  SH   ABCD.
Gọi N là hình chiếu của H trên cạnh BC. BC  HN BC   SH  BC  SHN  0,25  SBC  SHN 
Gọi K là hình chiếu của H trên cạnh SN. SBC  SHN  
SBC  SHN   SN HK  SN,HK   SHN   HK  SBC tại K
Vậy d H,SBC  HK. 1 1 1   a 3  SH  . 0,25 2 2 2 SH SA SD 2 1 1 1   a 21  a HK  . Vậy d H SBC 21 ,  . 0,25 2 2 2 HK SH HN 7 7 BM 3
Vì DM  SBC   B nên d M ,SBC 
d D,SBC  d D,SBC BD 4
Mà DH / / SBC  nên d D,SBC  d H,SBC. 0,25 3 3 a 21 3 21
Vậy d M ,SBC  d D,SBC  d H,SBC  .  . a 4 4 7 28
Một vật chuyển động trong 2 giờ theo quy luật 3 2
s  at  bt với t (h) là khoảng thời gian
tính từ lúc vật bắt đầu chuyển động và s (km) là quãng đường vật đi được trong khoảng thời
gian đó. Biết rằng kể từ lúc bắt đầu chuyển động, sau 1,5 giờ vận tốc của vật có giá trị lớn 1
nhất và sau 2 giờ vật có vận tốc bằng 4 (km/h). Đồ thị vận tốc của vật được minh họa như
hình vẽ bên. Tính quãng đường s mà vật di chuyển được trong 2 giờ đó. 2 v  3at  2bt 0,25  2b Câu 8   1,5  2.3a 0,25 (1,0  điểm) 12a   4b  4  2 a    3 0,25  b   3 2 3 2
s   t  3t , s   20 2  km 3 3 0,25 20
Vậy quãng đường s mà vật di chuyển được trong 2 giờ là km. 3