SỞ GIÁO DỤC VÀ ĐÀO TẠO KIỂM TRA HỌC KỲ II THÀNH PHỐ HỒ CHÍ MINH Năm học: 20192020 TRƯỜNG THPT BÌNH TÂN Môn: TOÁN 11 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút
(không kể thời gian phát đề) Câu 1. (1,5 điểm) Tính các giới hạn sau: 2 x  6x  8 a. lim . b. x x x . x  2 lim 9  3  5  3   2 x2 x  2x  8 c.  2 2 lim x  2x  3  x  x . x  Câu 2. (1,5 điểm) 2  x  5  3  khi x  2 
Cho hàm số f  x   x  2
. Xét liên tục của hàm số tại x  2 . 0  2  x  3 khi x  2  Câu 3. (2 điểm)
Tính đạo hàm của các hàm số sau: 1 a. 4 3
y  2x  x  2 x  4 . b. y  . x sin x  cos x . 3    c. 2 y  5 4x  6x 10 . d. 2 y  tan 2x    .  4  Câu 4. (1 điểm) Cho hàm số 3 2
y  x  3x  7x  2 có đồ thị (C) . Viết phương trình tiếp tuyến của đồ thị (C), biết
tiếp tuyến song song với đường thẳng  : y  4x  2020 . Câu 5. (4 điểm)
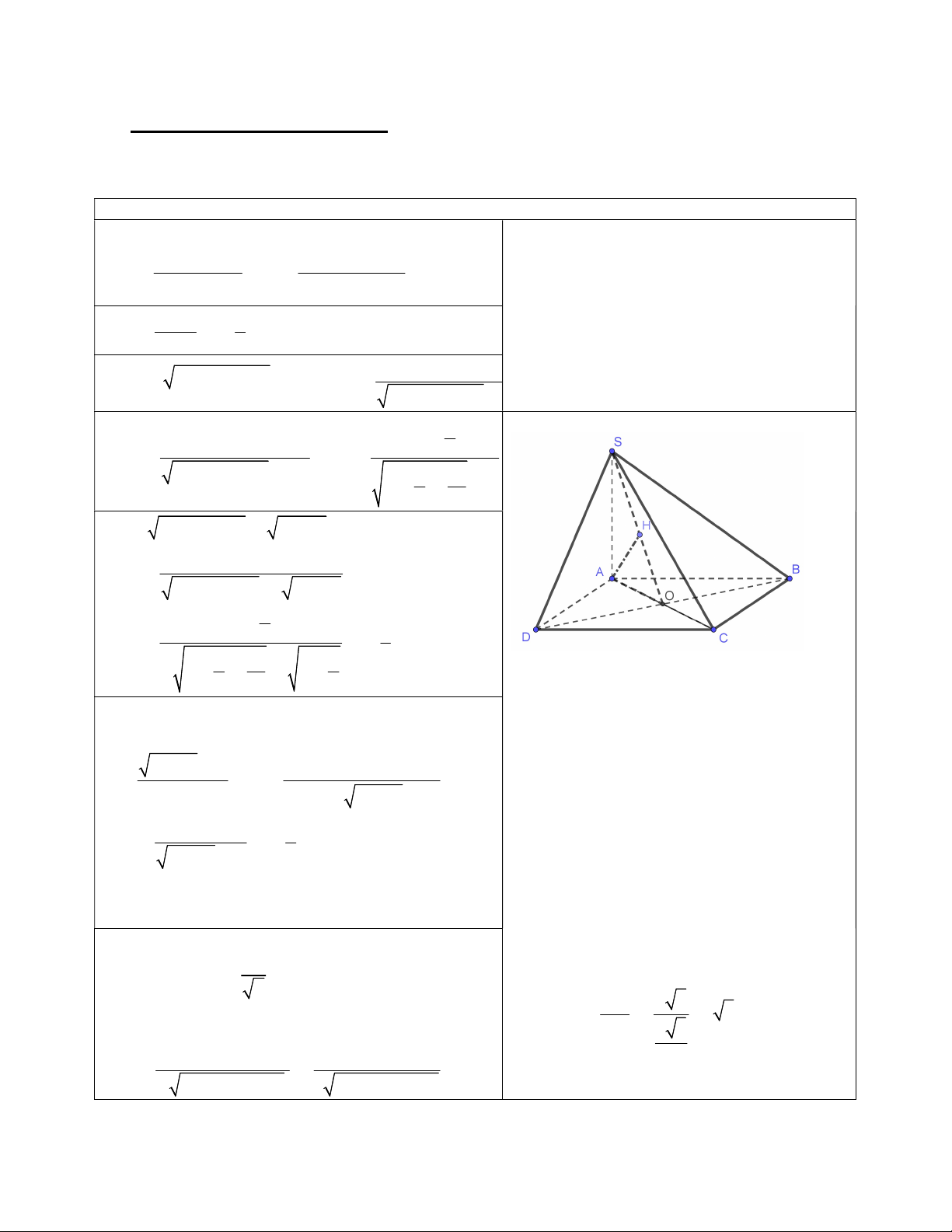
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a , SA  a 3 và SA  (ABCD) .
a. Chứng minh BC  (SAB) .
b. Chứng minh (SCD)  (SAD) .
c. Tính góc giữa đường thẳng SO và mặt phẳng (ABCD) .
d. Tính khoảng cách từ điểm A đến mặt phẳng (SBD) . -HẾT-
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐÁP ÁN THÀNH PHỐ HỒ CHÍ MINH
ĐỀ KIỂM TRA HỌC KỲ II TRƯỜNG THPT BÌNH TÂN Năm học: 2019−2020 Môn: TOÁN 11 Đề chính thức (Đáp án có 2 trang)
ĐÁP ÁN CHI TIẾT ĐỀ TOÁN 11 – HƯỚNG DẪN CHẤM Câu 1
Gọi M x ;y là tiếp điểm 0 0  2 x  6x  8 x 2x 4 a) lim  lim
Vì tiếp tuyến song song với đường thẳng 2 x 2  x 2 x  2x  8  x  2x  4
yx  4  3x 6x  7  4 0  2 nên 0 0 2 x  4 1
 x  2x  1  0  x  1 0 0 0  lim   x 2  x  4 3  y  7 0 2 3x  5 Pttt: y  4x  3 b) lim x  x   x  x  9 3 5 3  lim x 2 9x  3x  5  3x 5 Câu 5. 3 3x 5   x 1  lim  lim  x 2 9x  3x  5  3 x x  3 5 9    3 2 x x lim x  x   x  x x  2 2 2 3  x  3  lim x 2 2 x  2x  3  x  x 1 1  x 1  lim   x 2 3 1 2 B  C  S ; A BC  AB  1    1  2 x x x a) B
 C AB  ;A AB,SA   Câu 2.  SAB BC  f 2  1 SAB. 2 2 C  D  S ; A CD  AD x  5  3 x  4 b) lim  lim x2 x2 x  2 2 C
 D AD  D; A ,DSA   x  2 x  5  3  SAD    CD  x  2 2
SADmaCD SADSAD SAD  lim   x2 2 x  5  3 3 c)Taco :SA  Vì
nên hàm số không liên tục tại
ABCD AO là hình chiếu lim f x  f 2 x2     của SO lên mặt phẳng ABCD x  2 Câu 3
 SO ABCD  SO AO  ; ;  SOA 3 2 1 a)y  8x  x  Xét tam giác SAO : x  SA a 3 b)y  cosx  sinx tanSOA    6 AO a 2 5 2 4x 6x 1 0   58x  6 2 c)y   2 2 2 4x  6x  10 2 4x  6x  10       SO ABCD 0 ;  arctan 6  67 47 ' d)y  2 tan 2  x   .tan 2     x     4      4  
d)Gọi H là chiếu của SO            A  H  SO;AH  BD       2 2 tan 2x . 2  
  x   1  tan 2         x    4  4      4   b) S  O  BD  O  AH  SBD          S  , O BD   SBD 2  2 tan 2
 x  .2. 1  tan 2     x     4      4   Xét tam giác Câu 4. 2 y  3x  3x  7 S . AAO a 21 SAO :AH   2 2 SA  AO 7 a Vậy d A   SBD 21 ;   AH    7