SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2019 – 2020 THÀNH PHỐ HỒ CHÍ MINH Môn thi: TOÁN – KHỐI 11
TRƯỜNG THPT BÙI THỊ XUÂN Ngày thi: 17 / 06 / 2020
Thời gian làm bài: 90 phút, không kể thời gian phát đề
PHẦN ĐẠI SỐ (6 điểm) x 2 4x  x 1  3x
Bài 1: Tính giới hạn: lim . 2 x x  2 3 2  x  5x 12  x  2
Bài 2: Cho hàm số f  x     2x  4
. Định a để hàm số liên tục tại điểm x  2 .  2 3a  7  x  2
Bài 3: Tính đạo hàm các hàm số sau: a) 2 y  x  3x 1 .
b) y  2x  5.sin 3x . 3 2t 1
Bài 4: Một vật chuyển động có phương trình S t 
  6 , trong đó t (tính bằng giây) là thời 3 t
gian vật chuyển động kể từ lúc bắt đầu chuyển động t  0 và S (tính bằng mét) là quãng đường
vật đi được trong khoảng thời gian t . Tính vận tốc và gia tốc của vật tại thời điểm t  5s . Bài 5: Cho hàm số 3 2
y  x  3x 1 có đồ thị C  . Viết phương trình tiếp tuyến  của đồ thị C  ,
biết tiếp tuyến  song song đường thẳng d : y  9x  6 .
Bài 6: Chứng minh phương trình  2 m  m   4 2
6 x  x  2  0 luôn có nghiệm với mọi giá trị thực của tham số m .
PHẦN HÌNH HỌC (4 điểm)
Bài 7: Cho tứ diện SABC có SA , AB , AC đôi một vuông góc, biết SA  AB  AC  a . Gọi I là
trung điểm của đoạn BC .
a) Chứng minh đường thẳng SA vuông góc với mặt phẳng  ABC . Chứng minh mặt phẳng
SAB vuông góc với mặt phẳng SAC .
b) Chứng minh mặt phẳng SAI  vuông góc với mặt phẳng SBC .
c) Tính góc giữa hai mặt phẳng SAB và SAI  .
d) Trên tia đối của tia IA lấy điểm D sao cho ID  2IA và gọi E là trung điểm của đoạn SD .
Tính khoảng cách từ điểm E đến mặt phẳng SBC theo a .
------------ HẾT ------------
Thí sinh không sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm.
Họ tên thí sinh: ...................................................... SBD: .....................
KIỂM TRA HỌC KỲ II NĂM HỌC 2019 – 2020 ĐÁP ÁN TOÁN – KHỐI 11 ĐIỂM NỘI DUNG Bài 1 x  2 4x  x 1  3x (1đ) Tính giới hạn: lim . 2 x x  2  1 1  x  x 4    3x  2 x x   0.5đ  lim x 2  2  x 1  2   x 
(Học sinh làm đúng tử: cho 0,25đ; đúng mẫu: cho 0,25đ)   2 1 1 x  4    3 2 x x   0.25đ  lim x 2  2  x 1  2   x 
(Học sinh không ghi bước 1, mà bước 2 đúng: không trừ điểm) 1 1 4    3 2 0.25đ  lim x x  5 x 2 1 2 x 3 2  x  5x 12 Bài 2  x  2 Cho hàm số f  x     2x  4
. Định a để hàm số liên tục tại điểm x  2 . (1đ)  2 3a  7  x  2 0.25đ f   2 2  3a  7 x  5x 12 x  2 2 3 2 x  3x  6 0.25đ lim f  x  lim  lim x2 x2 x2 2x  4 2 x  2 2 x  3x  6 0.25đ  lim  4 x2 2 0.25đ
Hàm số liên tục tại điểm x  2  lim f  x  f 2 2
 3a  7  4  a  1 a  1  x2 Bài 3
Tính đạo hàm các hàm số sau: (1đ) a) 2 y  x  3x 1  2x 3x 1' 0.25đ y '  2 2 x  3x 1 2x  3 y '  0.25đ 2 2 x  3x 1
(Học sinh không ghi bước 1, mà kết quả đúng: không trừ điểm) b) y  2x 5.sin 3x . 0.25đ
y '  2x  5'.sin 3x  2x  5.sin 3x'
y '  2sin 3x  3.2x  5.cos3x 0.25đ
(Học sinh không ghi bước 1, mà kết quả đúng: không trừ điểm) 3 2t 1
Một vật chuyển động có phương trình S t 
  6 , trong đó t (tính bằng giây) là thời 3 t Bài 4
gian vật chuyển động kể từ lúc bắt đầu chuyển động t  0 và S (tính bằng mét) là quãng (1đ)
đường vật đi được trong khoảng thời gian t . Tính vận tốc và gia tốc của vật tại thời điểm t  5s . 1 0.25đ v t  S 't 2  2t  2 t 2 0.25đ
a t  v 't  4t  3 t 1251 0.25đ
Vận tốc của vật tại thời điểm t  5s : v5 
m / s (hoặc v5  50,04m / s ) 25 2498
Gia tốc của vật tại thời điểm t  5s : a 5   2 m / s  (hoặc a    2 5 19,984 m / s  ) 0.25đ 125
(HS không ghi đơn vị : không trừ điểm) Bài 5 Cho hàm số 3 2
y  x  3x 1 có đồ thị C  . Viết phương trình tiếp tuyến  của đồ thị C  , (1đ)
biết tiếp tuyến  song song đường thẳng d : y  9x  6 . 0.25đ 2 y '  3x  6x 0.25đ
Gọi M  x ; y là tiếp điểm. Do  / /d nên k  k  9 0 0   d 0.25đ Suy ra: 2
3x  6x  9  x  1 x  3  0 0 0 0
+ Với x  1  y  3. Phương trình tiếp tuyến: y  9 x  
1  3  y  9x  6 (loại) 0 0 0.25đ + Với x  3
  y  1. Phương trình tiếp tuyến: y  9x  3 1  y  9x  26 (nhận) 0 0
( – HS không loại một tiếp tuyến: trừ 0,25đ
– HS chỉ tìm 1 nghiệm x0 và viết đúng 1 phương trình tiếp tuyến: trừ 0,25đ) Bài 6
Chứng minh phương trình  2 m  m   4 2
6 x  x  2  0 luôn có nghiệm với mọi giá trị thực (1đ) của tham số m . 0.25đ Đặt f x   2 m  m   4 ( ) 2
6 x  x  2 ; f  x là hàm số xác định, liên tục trên  (1) 0.25đ f 0  2 0.25đ f   2
2  m  2m  6  0,m   Suy ra: f (0). f (2)  0, m    (2) 0.25đ
(1), (2)  phương trình f (x)  0 luôn có nghiệm, m    Bài 7
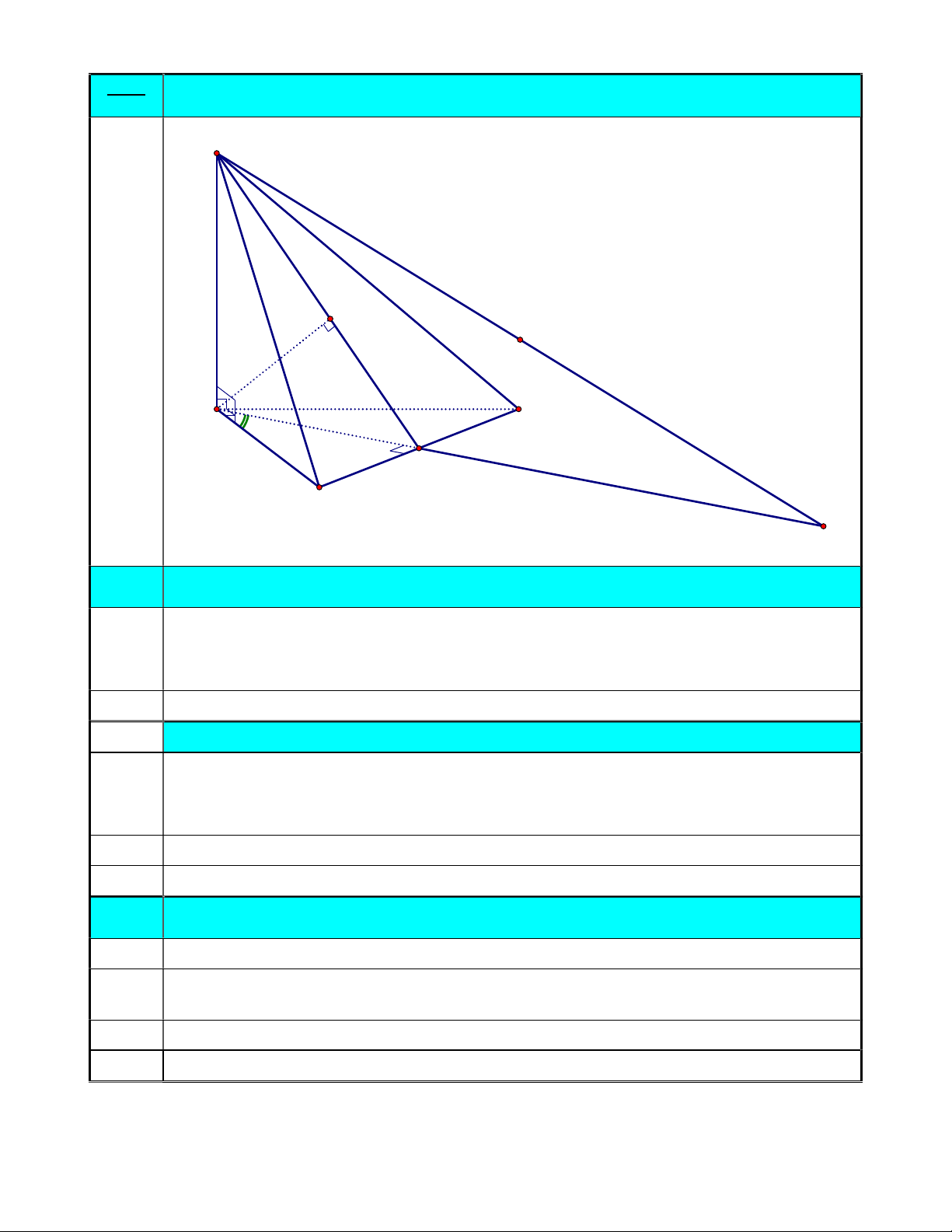
Cho tứ diện SABC có SA , AB , AC đôi một vuông góc, biết SA  AB  AC  a . Gọi I là (4đ)
trung điểm của đoạn BC . S a H E a A C a I B D a)
Chứng minh đường thẳng SA vuông góc với mặt phẳng  ABC . (1.5đ) SA  AB  gt  0.5đ SA  AC  gt
(Học sinh không giải thích lý do “gt”: không trừ điểm) 0.25đ  SA   ABC
Chứng minh mặt phẳng SAB vuông góc với mặt phẳng SAC  . AB  AC  gt  0.25đ AB  SA  gt
(Học sinh không giải thích lý do “gt”: không trừ điểm) 0.25đ  AB  SAC 0.25đ  SAB  SAC b)
Chứng minh mặt phẳng SAI  vuông góc với mặt phẳng SBC  . (1đ) 0.25đ AB  AC  gt  A
 BC cân tại A  trung tuyến AI cũng là đường cao  BC  AI BC  SA SA  ABCcmt 0.25đ
(Học sinh ghi được BC  AI và BC  SA , mà không giải thích lý do 1 trong 2 ý: trừ 0.25đ) 0.25đ Nên: BC  SAI  0.25đ  SBC  SAI  c)
Tính góc giữa hai mặt phẳng SAB và SAI  . (1đ) 
 SAB SAI   SA SA AB gt 0.25đ SA  AI  SA  ABCcmt
(Học sinh không giải thích lý do: không trừ điểm) 0.25đ  SAB,SAI    AB, AI    BAI 0.25đ
ABC vuông cân tại A nên trung tuyến AI cũng là phân giác trong 0.25đ   0
BAI  45 . Vậy SAB SAI   0 ,  45 d)
Trên tia đối của tia IA lấy điểm D sao cho ID  2IA và gọi E là trung điểm của đoạn SD .
(0.5đ) Tính khoảng cách từ điểm E đến mặt phẳng SBC  theo a .  d E SBC 1 ,  d D,SBC 0.25đ Lý luận: 2
  d E,SBC  d  , A SBC
d D,SBC  2d  , A SBC  
Trong SAI  kẻ AH  SI tại H Lý luận: d  , A SBC  AH 1 a 2 ABC : AI  BC  0.25đ 2 2 1 1 1 a 3 SAI :    AH  2 2 2 AH SA AI 3 a Vậy d E SBC 3 ,  3
Lưu ý: Học sinh giải cách khác đáp án, nếu đúng: cho trọn điểm