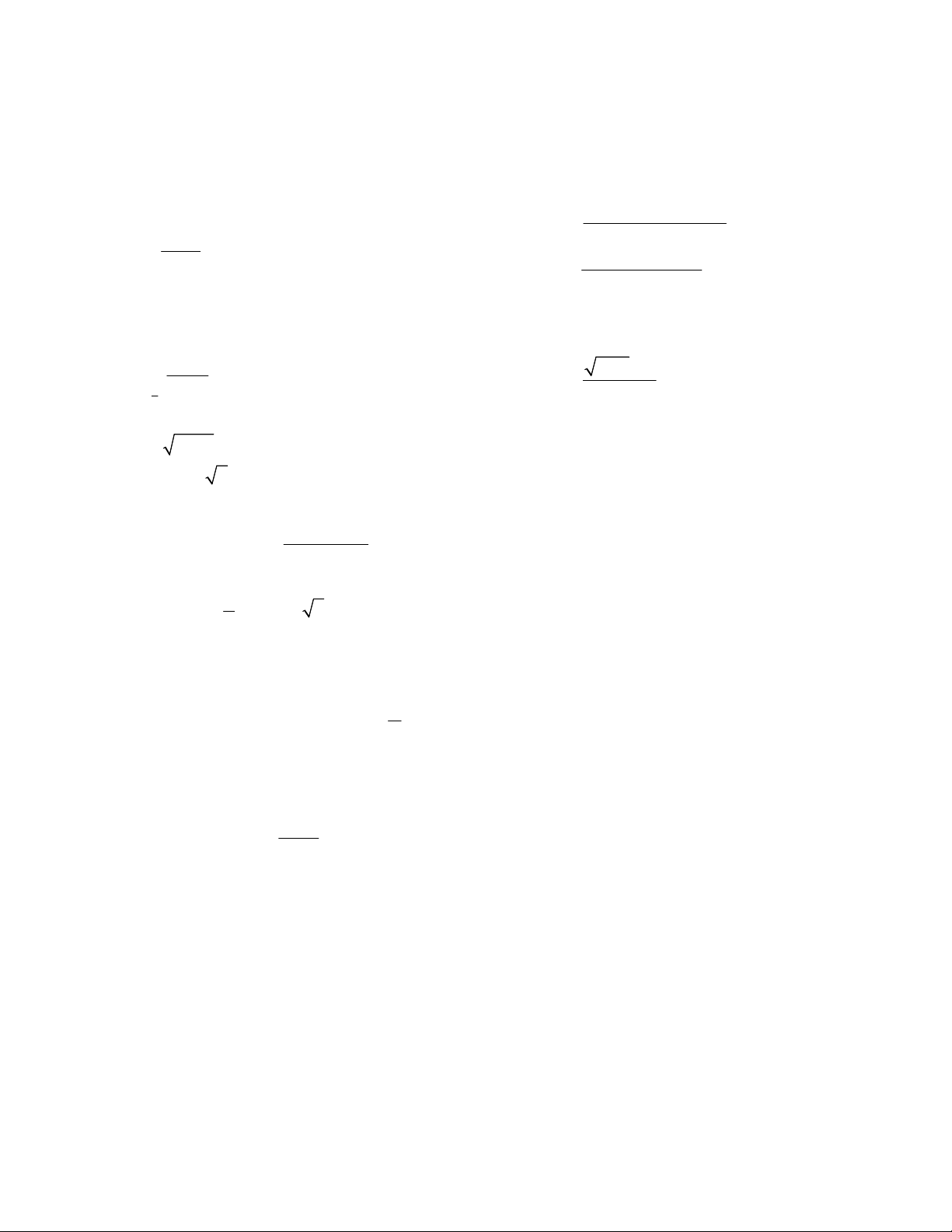


Preview text:
SỞ GD & ĐT TP HỒ CHÍ MINH
KIỂM TRA HỌC KÌ II- NĂM HỌC: 2019 - 2020
TRƯỜNG THPT ĐÔNG DƯƠNG MÔN: TOÁN – KHỐI 11 --------
Thời gian làm bài: 90 phút (Đề thi gồm 01 trang) ĐỀ BÀI
Bài 1: (1.0 điểm) Tìm giới hạn của dãy số: a) lim2n 3 3 2 4 n 3n 2n 1 c) lim 1 3n 3 2n n b) lim n 1 3 2 4 6 ... 2n d) lim n 6n 1
Bài 2: (1.0 điểm) Tính giới hạn của hàm số: a) 2 lim(x 2x 3) c) 3 2 lim x 2x x 1 ; x 1 x x 2 b) lim x 1 2 d) lim . 1 1 2x x x3 x 3 2
Bài 3: (1.0 điểm) Tìm đạo hàm của hàm số : a) 2 y x 1
c) y sin 2x 2cos x b) y x x 2 2 x 4 d) 2 y sin 5x Bài 4: (1.0 điểm) 2 3x 2x 5 a) Cho hàm số khi x 1 f (x) x 1
. Tìm giá trị của tham số a để hàm số liên tục tại x 1. 0 a khi x 1 b) Cho f x 1
; g(x) 2 x . Tính A f ' 1 2g ' 1 x Bài 5: (1.5 điểm)
a) Cho chuyển động xác định bởi phương trình 3 2
s t 3t 9t 2 (t được tính bằng giây, s được tính
bằng mét). Tìm gia tốc khi t 2s .
b) Cho hàm số y cot x . Tìm // y 4 Bài 6: (1.5 điểm)
a) Cho đường cong Ccó phương trình 3 2
y x 2x 3x 1. Gọi A là giao điểm của C với trục tung.
Tìm hệ số góc k của tiếp tuyến với (C) tại A. 3x 1 b) Cho hàm số y
có đồ thị (C). Viết phương trình tiếp tuyến với (C), biết tiếp tuyến song song x 2
với đường thẳng d: y 7x 3 Bài 7: (3.0 điểm)
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), SA = a.
a) (0.5đ) Chứng minh đường thẳng BC vuông góc mp (SAB).
b) (0.5đ) Chứng minh hai mặt phẳng (SBD) và (SAC) vuông góc.
c) (1.0đ)Tính tang của góc tạo bởi đường thẳng SC và mặt phẳng (ABCD)
d) (1.0đ) Gọi M là trung điểm SB, N là trung điểm SD, số đo góc giữa hai mặt phẳng (AMN) và
( ABCD) là . Tính cos .
---------------Hết---------------
Học sinh không được sử dụng tài liệu.
Giám thị coi thi không giải thích gì thêm. ĐÁP ÁN VÀ BIỂU ĐIỂM Câu Nội dung Điểm 1a 0.25 n 3 n n 3 lim 2 3 lim 2 lim .lim 2 n n 1b 1 n 0.25 1 1 3n 3 1 lim lim n 1 3 3 3 1c 3 2 1 0.25 3 2 4 2 3 4 n 3n 2n 1 lim lim n n n 2 3 2n n 1 2 2 n 1d n 0.25 2 2n 1 2 1 2 4 6 ... 2n n n 1 2 lim n n 6n lim lim lim 2 2 1 6n n 6n n 1 6 6 n 2a 2 lim(x 2x 3) 4 x 1 2b 0.25 x 5 lim 2 0 1 2 x 2 x 2 lim 1 2x 0; ; suy ra lim 1 1 1 2x x x 2 2 1 1 2x 0 khi x 2 2c 0.25 3 2 x x x 3 2 1 1 lim 2 1 l im x 1 ... 2 3 x x x x 2d 0.25 x x12 x12 1 2 1 1 lim lim lim x3 x3 x 3
x 3 x 1 2 x3 x 1 2 4 3a x 0.25 y ' x 1/ 2 2 x 1 3b 0.25 y x
x / x x x x / 2 2 1 ' 2 4 2 4 1 2
x 4 x 2 x .2x x 2 4 3x 5x x 4 x 3c / y 2 o c s2x 2sin x 0.25 3d / y 2sin 5 . x sin 5x' 2.sin 5 . x 5cos 5x 5sin10x 0.25 4a 2 3x 2x 5 Cho hàm số khi x 1 f (x) x 1
. Tìm giá trị của tham số a để hàm số a khi x 1 liên tục tại x 1. 0 3x 5 x 1 0.25 Tính lim f x lim lim3x 5 8 x 1 x 1 x 1 x 1 f 1 a
Hàm số liên tục tại x = 1 lim f (x) f (1) a 8 0.25 x 1 4b Cho f x 1
; g(x) 2 x . Tính A f ' 1 2g ' 1 x 0.25 f x 1 ' f ' 1 1 2 x g x 1 ' g ' 1 1 x A 1 2.1 1 0.25 5a
Cho chuyển động xác định bởi phương trình 3 2
s t 3t 9t 2 (t được tính bằng
giây, s được tính bằng mét). Tìm gia tốc khi t 2s . / s t 2 3t 6t 9 0.25 a t // s (t) 6t 6 0.25 a 2 6 0.25 5b
Cho hàm số y cot x . Tìm // y 4 y 2 ' 1 cot x 0.25 / / y x 2 2 cot 1 cot x 0.25 0.25 / / y 2.1 1 1 4 4 6a
Cho đường cong C có phương trình 3 2
y x 2x 3x 1. Gọi A là giao điểm của
C với trục tung. Tìm hệ số góc k của tiếp tuyến với (C) tại A. Ta có x 0 ; / 2 y 3x 4x 3 0.25 A
Hệ số góc k f '0 3 0.25 6b 3x 1 Cho hàm số y
có đồ thị (C). Viết phương trình tiếp tuyến với (C), biết tiếp x 2
tuyến song song với đường thẳng d: y 7x 3 7 0.25
Gọi M x ; y là tiếp điểm ; y '
, tiếp tuyến song song với đt d nên tiếp 0 0 x 22
tuyến có hệ số góc bằng 7 7 x 1 0.25 Ta có 0 7 x 22 x 3 0 0 Với x 1
y 4 . Suy ra pt tiếp tuyến: y 7x 3 (loại) 0.25 0 0
Với x 3 y 10 . Suy ra pt tiếp tuyến: y 7x 31 0.25 0 0 7 7a
Chứng minh đường thẳng BC vuông góc mp (SAB) SA ABCD 0.25 Ta có: SA BC BC ABCD BC AB(gt) 0.25 BC SAB BC S ( A cmt) 7b
Chứng minh hai mặt phẳng (SBD) và (SAC) vuông góc. SA ABCD BD AC(tchv) 0.25 ; BD SAC SA BD BD ABCD BD S ( A cmt) BD SAC 0.25 SBD SAC BD SBD 7c
Tính tang của góc tạo bởi đường thẳng SC và mặt phẳng (ABCD)
Hình chiếu của SC lên mp (ABCD) là AC nên: SC, ABCD SC, AC ACS 0.25
Tính được AC = a AC a 2 0.25 SA ABCD 0.25 SA AC AC ABCD SA 0.25
Trong tam giác SAC vuông tại A, 1 tan C AC 2 KL 7d
Gọi M là trung điểm SB, N là trung điểm SD, số đo góc giữa hai mặt phẳng
( AMN ) và ( ABCD) là . Tính cos .
Tam giác SAB và SAD là tam giác vuông cân tại A nên AM SB, AN SD BC SAB AM BC AM SAB AM SB AM SC , 0.25 AM BC
Chứng minh tương tự: AN SC . Suy ra: AMN SC 0.25 AMN SC 0.25
AMN , ABCD SC,SA= ABCD CSA SA 2 2 SC SA AC a 3 SA 1 cos 0.25 SC 3




