SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM
ĐỀ KIỂM TRA HỌC KỲ 2
TRƯỜNG THPT HOÀNG HOA THÁM Năm học: 2019 – 2020 Môn: TOÁN – Lớp 11
Thời gian làm bài: 90 phút, không kể thời gian phát đề. 2 Câu 1 (1,0 điểm). Tính x  x  1  2x  1 lim . x x  10  ax  2 3 a (x  1)
Câu 2 (1,0 điểm). Cho hàm số  f(x)   x  1 . (x   1)  x  3  2
Xác định a để hàm số f x  liên tục tại x  1. 0
Câu 3 (3,0 điểm). Tính đạo hàm các hàm số sau: a) 2x  1 y  x  4 b) y  x  x  2 2 5 x   x  c) y  2020 sin   .  8 2 
Câu 4 (1,0 điểm). Cho hàm số y  x.cosx. Chứng minh rằng: x.y  2(y ' cosx)  x.y '  0.
Câu 5 (1,0 điểm). Viết phương trình tiếp tuyến  với đồ thị   :  x C y biết tiếp 2x  3
tuyến song song với đường thẳng d : y  3x  4 .
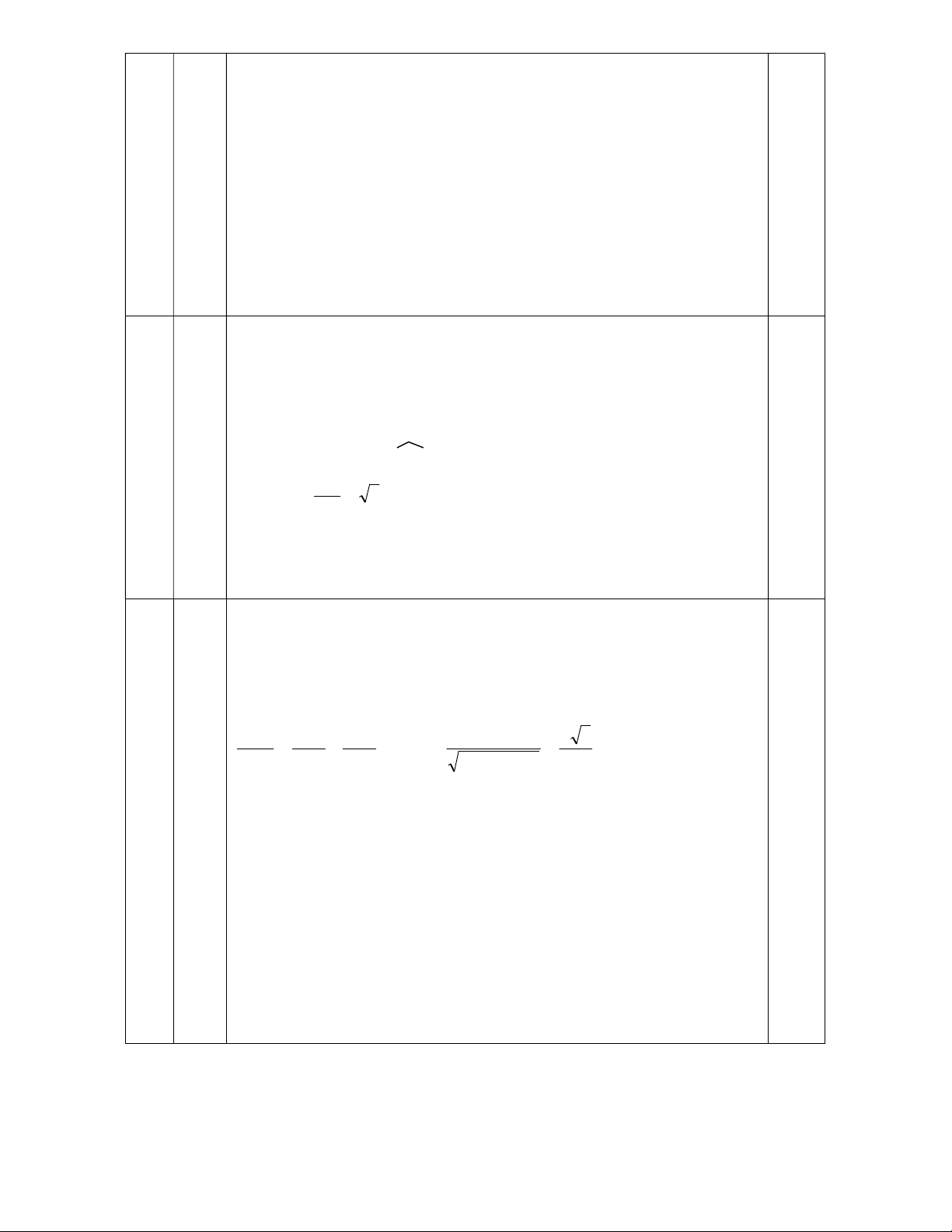
Câu 6 (3,0 điểm). Cho hình chóp S.ABCD với ABCD là hình vuông có cạnh bằng 2a , H là
trung điểm của AB , SH  ABCD và SH  a 3 .
a) Chứng minh SBC   SAB .
b) Xác định và tính góc giữa SAD và ABCD.
c) Tính theo a khoảng cách từ điểm H đến mặt phẳng SAD . -----HẾT-----
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ, tên thí sinh:. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh:. . . . . . . . . . . . . . . . . . . THPT HOÀNG HOA THÁM NHÓM TOÁN 11
ĐÁP ÁN KIỂM TRA HỌC KÌ II – NĂM HỌC 2019 – 2020 MÔN TOÁN LỚP 11 CÂ Ý NỘI DUNG ĐIỂ U M 1 2 x  x  1  2x 1 (1đ) lim x x 10 1 1  x 1   2x 1 2  lim x x 0.25 x x  10 1 1 1  1   2  2  lim x x x x 10 1 0.25x x 2  3  0.25 2 3ax  2 a (x  ) 1 (1đ)  f (x)   x 1  (x  ) 1  x  3  2 f ) 1 ( 3 2 a a 0.25 limf ( ) x  3 2 aa x 1  x 1  0.25 lim f ( ) x  lim  li ( m x3  ) 2  4 x 1  x 1  x3 2 x 1 
do f(x) liên tục tại x0=1 0.25  f ) 1 (  lim f (x)  lim f (x) x 1  x 1   3 2
a  a  4  a  1 , a  4 0.25 3 a) 2 x  1 (3đ) (1đ) y   x  4 (2 x  ) 1 ' ( x  4)  (2 x  ) 1 ( x  4)' y '  0.25x 2 ( x  4) 2 9  2 ( x  4)
.......... .......... .......... .......... .......... .......... .......... ....... b) 0.25x (1đ) 2 y  x 2  5 x  x 2 2 2
y '  ( x)' 2  5 x  x  x( 2  5 x  x )' …….  5  2 x 2  2  5 x  x  x 2 2 2  5 x  x c) 0.25x (1đ)  x 2 y  sin2020(  ) 8 2  x  x 0.25x
 y' 2020sin2019(  ) (sin(  ))/ 8 2 8 2 2  x  x  x
 2020sin2019(  ) (  )/ cos(  ) 8 2 8 2 8 2  x  x  1
 010sin2019(  )cos(  ) 8 2 8 2 0.25x 2 0.25 0.25 4
y  x.cos x  y'  ( x)' cos x  x(cos x)' 0.25 (1đ)  cos x  x.sin x 0.25x
y' cos x  x sin x  cos x  x.sin x  cos x  x sin x  0 (đpcm) 2 0.25 5
Gọi (x0;y0) là tiếp điểm,(t) là tiếp tuyến (1đ)  x y  y  3 ' 2x  3 (2x  3)2 0.25
(t) // d : y  3x  4  f ' (x )  3 0 0.25 3 x  1  y  1   3  2  0 0 (2x  3) x y 0   2   2 0 0 0.25  y  3x  2 pttt :   y  3x  8 0.25 6 S (3đ) K D A I H B 2a C a) Chứng minh: (SBC)  (SAB) (1đ) BC  AB(ABCD . h vuông) 0.25
BC  SH (vì SH  ( ABCD), BC  ( ABCD)) 0.25  BC  (SAB) BC  (SBC) 0.25  (SBC)  (SAB) 0.25 b) (SAD)  (ABCD)  AD (1đ) AH  AD SH  AD  AD  (SAH )  SA  AD  0.25 [(SAD),(ABCD)]  SAH SH 0 tan SAH   3  SAH  60 0.25 HA 0.25x 2 c). Ve HK  SA,mà HK  AD (1đ)  HK  (SAD) 0.25  d[H ,(SAD)]  HK 0.25  SHA có HK đường cao 1 1 1 HS.HA a 3    HK   2 2 2 2 2 HK HS HA HS  HA 2 0.25x 2