MA TRẬN ĐỀ KIỂM TRA HỌC KÌ 2
MÔN TOÁN LỚP 11 NĂM HỌC 2019 – 2020 CHỦ ĐỀ NB TH VD VDC TỔNG Giới hạn Giới hạn dãy số . 1 1 (3 điểm) Giới hạn hàm số . 1 1 2 Hàm số Xét tính liên tục của 0.75 0.75 liên tục
hàm số tại một điểm. (1,5 điểm) Ứng dụng của tính 0.75 0.75 liên tục. Tính đạo hàm của hàm 1 1 Đạo hàm số. ( 2 điểm) Viết phương trình tiếp
tuyến của đồ thị hàm 1 1 sô. Quan hệ Mặt phẳng vuông góc vuông góc mặt phẳng. 1 1 ( 1 điểm) Góc giữa đường thẳng Góc với mặt phẳng 1 1 ( 2 điểm) Góc giữa hai mặt 1 1 phẳng. Khoảng Khoảng cách từ một cách 0.5 0.5
( 0.5 điểm) điểm đến mặt phẳng.
SỞ GIÁO DỤC VÀ ĐÀO TẠO TPHCM
Trường THPT Mạc Đĩnh Chi
ĐỀ KIỂM TRA HỌC KỲ II – NĂM HỌC 2019 – 2020
MÔN TOÁN – Khối 11 (Từ 11A02 đến 11A24) Thời gian: 90 phút
Bài 1: (3 điểm) Tính các giới hạn sau: n n a) 2  3.5 lim . 5n  3n b) x  2 2 lim . 3 x 2  x  3x  2 c) 2 lim ( x  2x  7  x). x Bài 2: (1,5 điểm) 2 x 4x  3  , khi x  1 a) Cho hàm số 3 f(x)   x 1  4  , khi x  1  3
Xét tính liên tục của hàm số f (x) tại điểm x  1. 0
b) Chứng minh phương trình 5 3
2x  4x  x  6  0 có ít nhất một nghiệm dương. Bài 3: (2 điểm) a)  x
Tính đạo hàm của hàm số 1 y  . 1x b) Cho hàm số 3 2
y  x  3x có đồ thị C. Viết phương trình tiếp tuyến của đồ thị
C tại điểm có hoành độ x  1  . 0 Bài 4: (3,5 điểm)
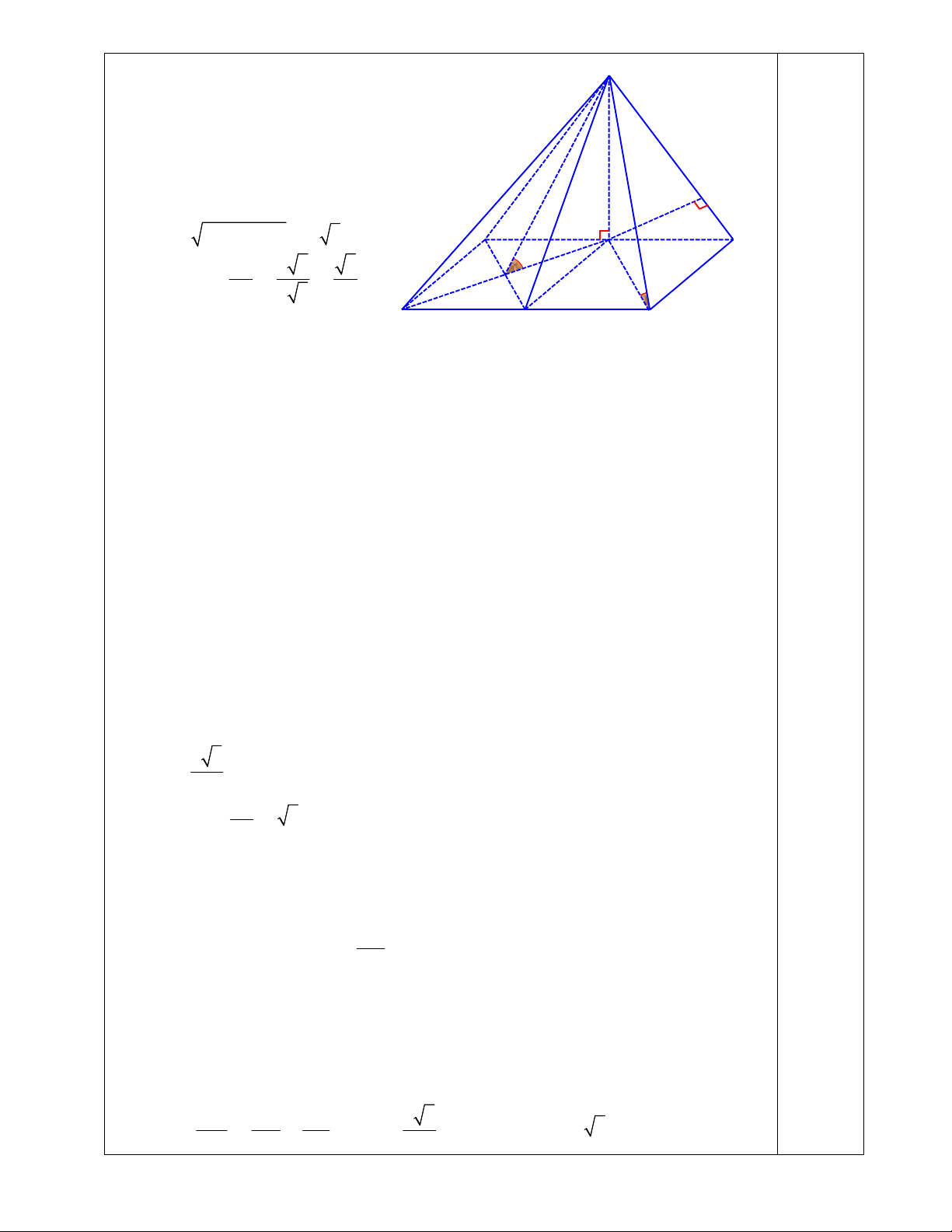
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Gọi I,J lần lượt là
trung điểm của AB và CD , SI vuông góc với mặt phẳng (ABCD). Biết AB  2a , BC  a , SI  a 3 .
a) Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
b) Chứng minh SCD  SIJ.
c) Tính góc giữa hai mặt phẳng SAJ và (ABCD).
d) Tính khoảng cách từ điểm D đến mặt phẳng SBC.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . HẾT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ĐÁP ÁN Bài 1: (3 điểm)   n   n 2n 5 .  3 2      3 n n 5n     0.5 a) 2  3.5 lim lim   5 lim    3 5n  3n   n 0,25 n  3n 5 . 1     3    5n  1    5 0.25 b) x  2  2 x  2  4 lim  lim 3 x 2  x 2 x  3x  2
  3x 3x  2 x 2 2 0,25 0,25 x  2  lim 1 1  lim  0,25
x2 x 2 2x  2x  1 x 2 2 x2  2x  x   x    36 2 1 2 2 0,25 7 2  c) 2
lim ( x  2x  7  x)  2x  7 lim ( )  lim ( x )  1 0.5 x x 2 x  2x  7  x x 2 7  1   1 0.25 2 x x 0.25 Bài 2: (1,5 điểm) 2 a) x  4x  3 x  3 2 lim f(x)  lim  lim   (1) 0.25 3 2 x 1  x 1  x 1 x 1  x  x  1 3 4 f (1)  (2) 0.25 3
(1), (2)  lim f(x)  f(1)  Hàm số f (x) không liên tục tại x  1. 0.25 x 1  0 b) Đặt 5 3
f(x)  2x  4x  x  6
Hàm số f (x) xác định và liên tục trên   f (x) liên tục trên đoạn 0;2   0.25
Ta có f(0)  6; f(2)  28  f(0).f(2)  168  0
 tồn tại số x  0;2 sao cho f(x )  0 0.25 0   0  pt 5 3
2x  4x  x  6  0 có ít nhất một nghiệm dương. 0.25 Bài 3: (2 điểm)
(1  x)'. 1  x (1  x). 1x ' a) 1  x y   y '  0.5 1 x 1  x 1 0.25 0.25 1  x  (1  x) 2(1 x)  (1  x) 2 1  x  2 1  x 3  x   1  x 1 x 2(1 x) 1 x
b) Ta có x  1  y  4  0.25 0 0 2 y '  3x  6x  y '( 1  )  9 0.25+0.25
Phương trình tiếp tuyến tại M(1;4) là : y  9(x  1) 4  y  9x  5 0.25 Bài 4: (3,5 điểm) S a)  SC;(ABCD)  ?   Vì SI  ABCD
 IC là hình chiếu của SC lên ABCD 0,25   SC ABCD   H   SC IC    ;( ) ;  SCI 0,25 2 2 IC  IB  BC  a 2 A B 0,25 I  SI a 3 6 tanSCI    IC O a 2 2  0  SCI  50 46' D J C 0.25
b) Chứng minh SCD  SIJ.
Ta có IJ là đường trung bình của hình chữ nhật ABCD
 IJ // BC , mà BC  CD  IJ  CD 0.25
Mặt khác SI  CD SI  (ABCD ) 0.25 CD  SIJ 0.25
Mà CD  SCD  SCD  SIJ 0.25 c) SAJ   ABDC  ;   ?  (SAJ)  (ABCD)  AJ
Ta có AIJD là hình vuông  AJ  ID 0.25
Mặt khác AJ  SI SI  (ABCD )  AJ  SDI  AJ  SO   SAJ ABCD     0.25   SO IO   ( );( ) ;  SOI a 2 OI  0.25 2  tan SI SOI   6  0  SOI  67 47 ' 0.25 IO d) d D;  SBC   ? 
Ta có AD //BC  AD // SBC d D;  SBC  d  ; A   SBC       
Vì AI cắt SBC tại B và AB  2 d  ; A  SBC 2.d I;   SBC    IB  0.25 Kẻ IH  SB tại H B  C  AB Ta có 
 BC  SAB  BC  IH B  C  SI  Mà IH  SB IH
SBC d I;SBC     IH  Ta có 1 1 1 a 3    IH  d D; 02.5  SBC    a 3 2 2 2 IH IB IS 2 