SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2019 -2020 TP HỒ CHÍ MINH MÔN TOÁN - Khối 11
TRƯỜNG THPT NGUYỄN CHÍ THANH
Thời gian làm bài 90 phút
(Không tính thời gian phát đề ) ĐỀ CHÍNH THỨC
Bài 1 : (2,0 điểm) Tính các giới hạn sau: 3 2 x 3x  2 a. lim 2 x 1
 x  4x  3 b.  2 lim
x  x 1  x   x  2
 3x  x  2  ; x 1  
Bài 2: (1,0 điểm) Tìm m để hàm số x 1 f (x)  
liên tục tại x  1 . 0  5 m  x  ; x 1  4
Bài 3: (1,0 điểm) Tính đạo hàm của các hàm số sau: 2 x  2x 1 a. y  x 1 b. 2
y  (3x 2) 1 x x 
Bài 4: (1,0 điểm) Cho hàm số y  f x 3 1 
có đồ thị (C). Viết phương trình tiếp tuyến x 1
của (C) biết tiếp tuyến song song với đường thẳng: d : x  4 y  21 0 .
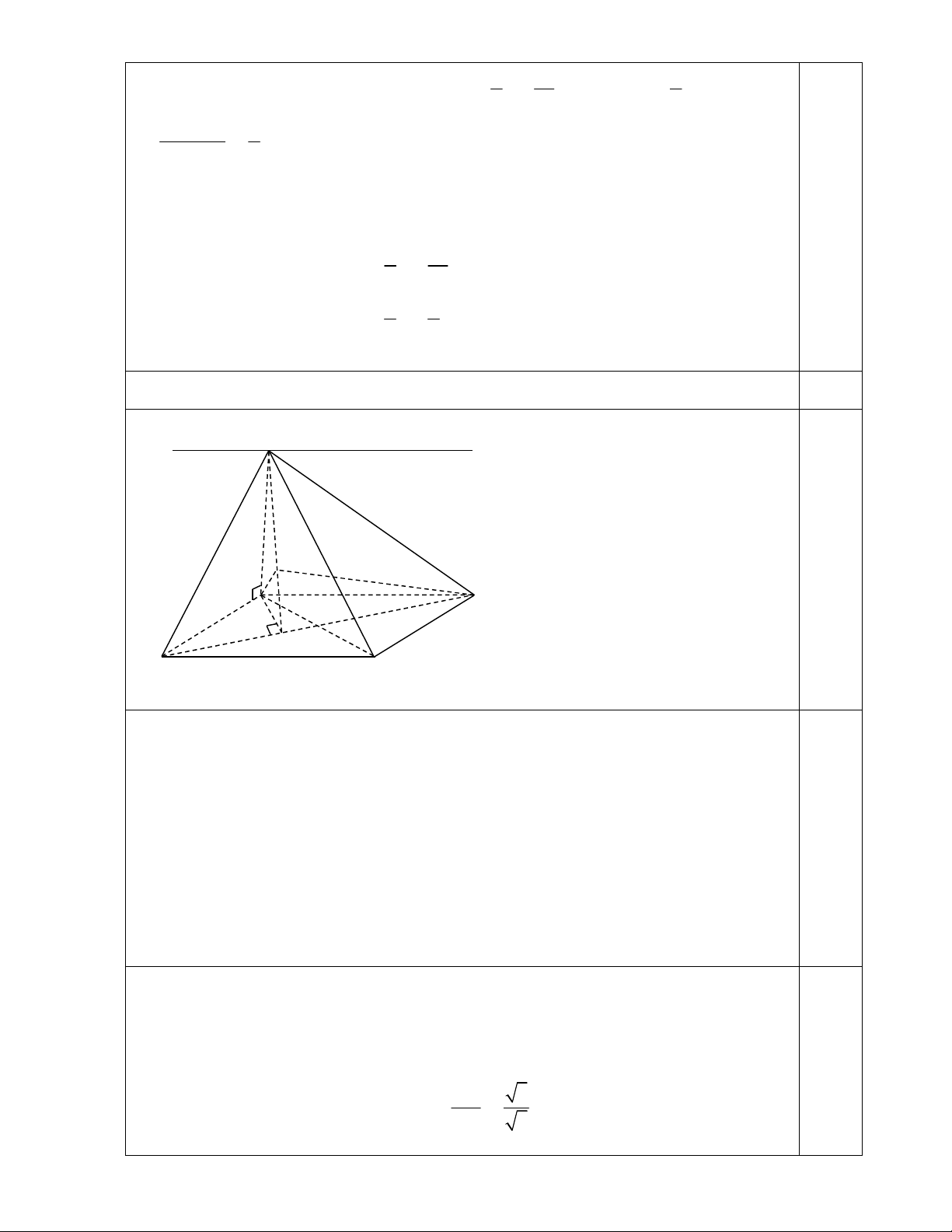
Bài 5 : (4,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, biết AB  2a ,
AD  a , SA  (ABCD) và SA = a 3 .
a) Chứng minh: BC  (SAB) , DC  (SAD)
b) Tính góc giữa SC và mặt phẳng (ABCD).
c) Gọi H là hình chiếu của A trên BD, K là hình chiếu của A trên SH.
Chứng minh:  ABK   SBD .
d) Tính góc giữa hai mặt phẳng (SAB) và (SCD).
Bài 6: (1,0 điểm) Tính giới hạn sau: x 2 2 lim
x  2x  2 x  x  x   x HẾT
ĐÁP ÁN MÔN TOÁN K11 – HỌC KỲ 2 – 2019-2020 Bài 1: 2 điểm Điểm   x  1 0.25+ x x  2 3 2 x  2x  2 3 2  a. lim  lim 0.25 2 x 1    x 1 x 4x 3  x  1 x   3 2 x  2x  2 3  lim  0.25+ x 1  x  3 2 0.25 x 1 b. lim     0.5  2 x x 1 x lim x x 2
x  x 1  x 1 1 1  lim x  0.25+ x 1 1 2 0.25 1  1 2 x x Bài 2: 1 điểm 11 0.25
f (1)  lim f (x)  m   x 1  4 2 2 3x  x  2 3x  x  4
lim f (x)  lim  lim    0.25 x 1  x 1  x 1 x 1  x  1  2
3x  x  2 3x  4 7  0.25 lim    2 x 1   4 3x x 2 5 7 0.25
Hàm số liên tục tại x  1  lim f x  lim f x  f 1  m    m  3 0         x 1  x 1  4 4 Bài 3: 1điểm 2 2 x  2x 1 x  2x  3 0.5 a. y   y  2 x 1 (x 1) 0.25 b. 2 y  
 x  y   x   2
 x  x    2 (3 x 2) 1 3 2 '. 1 3 2 . 1 x ' 2   2 x 6x 2x 3
 3 1 x  (3x  2).  2 2 1 x 1 x 0.25 Bài 4: 1 điểm 4
TXĐ: D   \  
1 , f x   1 x2
Gọi M (x ; y ) là tiếp điểm của (C) và tiếp tuyến 0 0 0 1 21 1 0.25
Tiếp tuyến song song với đường thẳng d : y  x 
nên f x   4 4 0 4 4 1    1 x 2 4 0 x  5 0.25 0   x  3  0 1 21
x  5  y  4 
 pttt : y  x  (loại) 0.25 0 0 4 4 1 5 x  3
  y  2 pttt : y  x  (nhận) 0.25 0 0 4 4
Hs quên loại thì trừ 0,25 Bài 5: 4 điểm x' S x K A B H D C
a. Chứng minh: BC  (SAB), DC  (SAD)
 BC  AB (do ABCD là hình chữ nhật) 0.25
 BC  SA (do SA  (ABCD)
 BC  (SAB) 0.25
 DC  AD (do ABCD là hình chữ nhật) 0.25
 DC  SA (do SA  (ABCD)
 DC  (SAD) 0.25
b. Tính góc giữa SC và mặt phẳng (ABCD).
 SA  ( ABCD) tại A  AC là hình chiếu của SC lên (ABCD) 0.25    0.25
(SC, ( ABCD))  (SC, AC)  SA 3
 SAC vuông tại A nên tan SCA   0.25 AC 5 15   0  SCA  arctan
 37,8 . Vậy SC ABCD    15 ,  arctan 5 5 0.25
c. Chứng minh:  ABK   SBD AH  BD   0.25
SA  BD SA  ABCD BD SAH  
AK  BD BD  SAH , AK SAH  0.25
AK  SH , SH  SBD, SH  BD  H
 AK  SBD 0.25   0.25
ABK   SBD
d. Góc giữa (SAB) và (SCD)
(SAB)  (SCD)  x Sx  , (Sx/ / AB/ / CD) 0.25 C
 D  SD (do CD  (SAD))  Trong (SCD) có   SD  Sx  Sx / /CD  SA  AB  Trong (SAB) có   SA  Sx 0.25 A  B/ /Sx  Vậy   SAB SCD   ( ), ( )  ( , SA SD) 0.25  AD 1  0 tan ASD  
 ASD  30 . Vậy   SAB SCD  0 ( ), ( )  30 0.25 SA 3 Bài 6: 1điểm 2 2 x
x  x  x  lim x      0.25   2 2 1 2 2 x 2x x 2 x x    lim x x  2 2
x  2x  x  2 x  x  2 2x   1  lim x  2 2
x  2x  x  2 x  x  2
x  2x  x   1 2 1 0.25  lim   x   2 1   2 1 4 
 1 1 2 1  1 1      x x   x x 0.25+ 0.25