SỞ GD&ĐT TP. HỒ CHÍ MINH ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2019 - 2020 TRƯỜNG THPT TÂN TÚC Môn: Toán; Lớp 11
Thời gian làm bài: 90 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC
(Đề kiểm tra có 01 trang)
Câu 1 (2,0 điểm). Tính giới hạn của các hàm số sau: 2 4x  5x 1 2 x  x  7  3 a) lim . b) lim . 2 x x  6x  3 x2 4x  8
Câu 2 (2,0 điểm).Tìm đạo hàm của các hàm số sau: 2x 1 a) y  . b) 4 y  x  5x  x. c) y  sin 2x   1 cos x   1 . x 1 Câu 3 (2,0 điểm). 3 x a) Cho hàm số 2 y 
 x 1. Giải bất phương trình y ' x  6  0. 3 1 b) Cho hàm số 3 2
y  f (x)  x  3x  8x  7 có đồ thị C. Viết phương trình tiếp tuyến với C, 3
biết tiếp tuyến có hệ số góc bằng 1  . 1
Câu 4 (1,0 điểm). Cho hàm số f  x 3   x  m  2 2 x   2
m 10 x  m 1, (m là tham số). Tìm tất cả 3
các giá trị của tham số m để f ' x  0, x    S
Câu 5 (2,5 điểm). Cho hình chóp đều tứ giác S.ABCD (hình vẽ bên), a AB  6 a, SA 
. Gọi O là giao điểm của AC và BD; gọi M là trung điểm 3 của cạnh BC. A D
a) Chứng minh BC  SMO và SAC  SBD.
b) Tính góc giữa cạnh bên và mặt đáy của hình chóp đã cho. O B
c) Tính khoảng cách từ điểm O đến mặt phẳng SBC, từ đó suy ra C
khoảng cách từ điểm A đến mặt phẳng SBC.
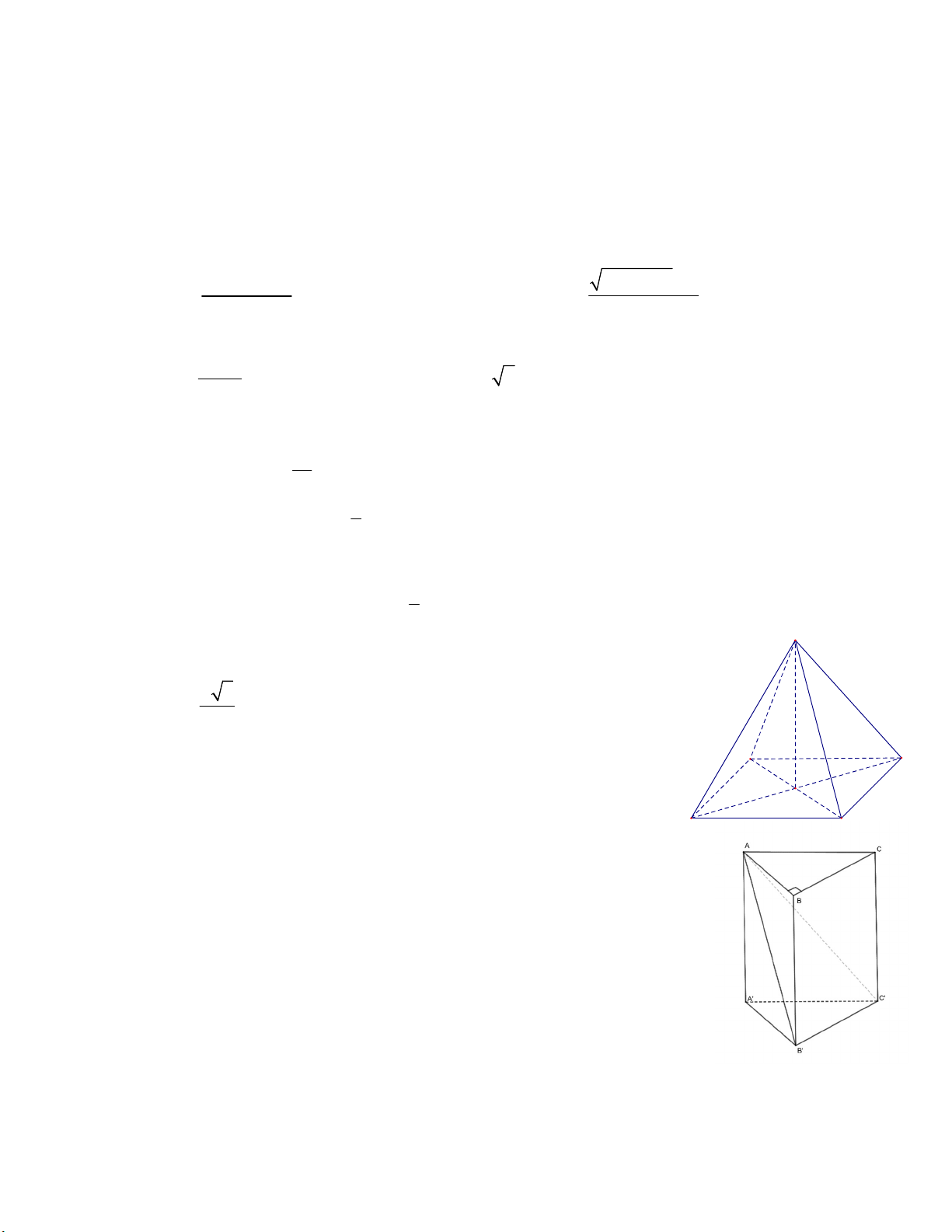
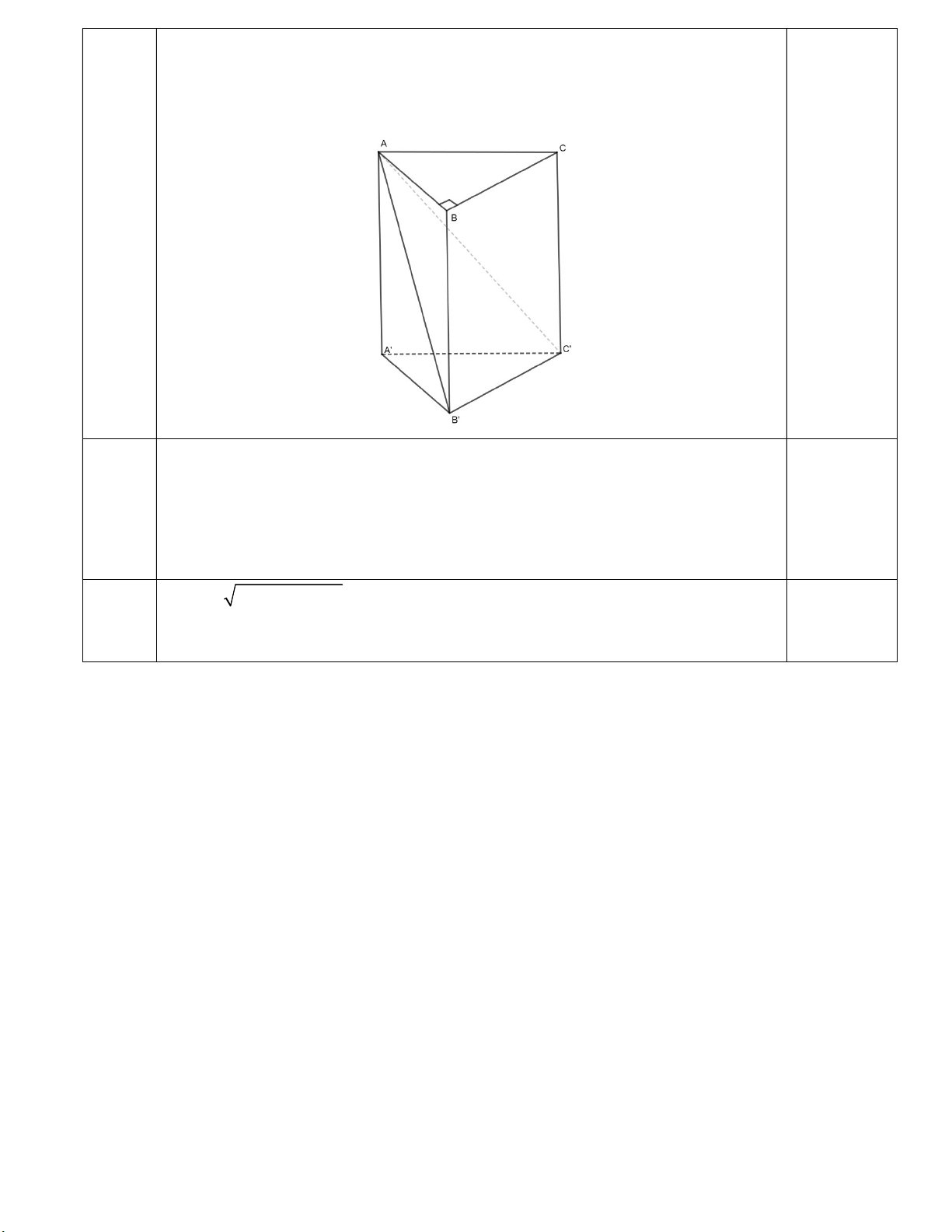
Câu 6 (0,5 điểm). Cho lăng trụ đứng ABC.A' B 'C ' (hình vẽ bên) có đáy là tam giác vuông tại , B AC  5 , a BC  3 ,
a góc giữa mặt phẳng  AB 'C ' và mặt đáy bằng 0
45 .Tính độ dài đường cao của lăng trụ đã cho.
-----------------HẾT-----------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:…………………………; Số báo danh:.………….;Lớp:……..
SỞ GIÁO DỤC VÀ ĐÀO TẠO TPHCM
ĐÁP ÁN ĐỀ THI HKII – NH: 2019 – 2020 TRƯỜNG THPT TÂN TÚC MÔN TOÁN KHỐI 11 THỜI GIAN: 90 PHÚT Câu Nội dung Điểm
Câu 1 Tính các giới hạn sau (2,0 điểm) a) 2 4x  5x 1 lim 2 x x  6x  3 0.25 2  5 1  x 4    2   x x lim   0.25 x 2  6 3  x 1     2   x x  5 1 0.25 4   2  lim x x x 6 3 1  2 x x  4  0.25 b) 2 x  x  7  3 lim x2 4x  8  x  x  7 2 2 2  3  lim 0.25
x2 4x 8 2x  x  7 3 x 2x  1 0.25  lim 0.25
x2 x  2.4. 2x  x 7 3 x 1 0.25  1 lim  .
x2 4. 2x  x 7 3 8 Câu 2
Tính đạo hàm của hàm số 2 điểm a) 2x 1 y  . . x 1 2 x   1  2x   1 3 0.25+0.25 y   x  2 1 x  2 1 b) 4 y  x  5x  x 1 0.25 3 y '  4x  5  2 x +0.25+0.25 c) y  sin 2x   1 cos x   1 y '  sin 2x   1 'cos x   1  cos x   1 'sin 2x   1 0.25
y '  2cos 2xcos x   1  sin xsin 2x   1 0.25+0.25 Câu 3 2 điểm a) 3 x 1 điểm Cho 2 y 
 x 1. Tìm tất cả các nghiệm của bất phương trình y' x  6  0. 3 2 y '  x  2 . x 0.25 y ' x  6  0   2 x  2x  x  6  0 0.25 2  x  x  6  0  2  x  3. 0.5
Kết luận: S  2;  3 . b) 1 1 điểm Cho hàm số 3 2
y  f (x)  x  3x  8x  7 có đồ thị C . Viết phương trình tiếp 3
tuyến với C biết tiếp tuyến có hệ số góc bằng 1  . y  f  x 2  x  6x  8. 0.25
Vì tiếp tuyến có hệ số góc bằng 1  .nên f 'x  1  . 0.25 0  Từ đó ta có 2
x  6x  9  0  x  3  0.25 0 0 0
Vậy phương trình tiếp tuyến cần tìm là: y  x 16. 0.25 Câu 4 1 (1 điểm). Cho hàm số f  x 3   x  m  2 2 x   2
m 10 x  m 1, (m là tham số). Tìm 3
tất cả các giá trị của tham số m để f ' x  0, x    Đkbt khi f  x 2  x  m   2 2
2 x  m 10  0  x   . 0.25 a  1  0 0.5   . 2
  2m  4m  6  0  3   m 1. 0.25 Câu 5 a 2.5 điểm
Cho hình chóp đều tứ giác S.ABCD (hình vẽ bên), AB  6 a, SA  . Gọi O là 3
giao điểm của AC và BD; gọi M là trung điểm của cạnh BC. Ta có:
O là tâm của hình vuông ABCD .
Mà S.ABCD là hình chóp đều. Suy ra SO   ABCD. a)
Chứng minh BC  SMO và SAC  SBD. 1.0 BC  OM 0.5 BC   SO  BC  SOM . AC  BD 0.25 AC   SO  AC  SBD. Mà AC  SAC . 0.25
Suy ra SAC  SBD. b)
Tính góc giữa cạnh bên và mặt đáy của hình chóp đã cho. 0.5
Hình chiếu vuông góc của SB lên mp  ABCD là OB.
Suy ra góc giữa SB và mp  ABCD là  SBO . 0.25 BD a 2 OB   2 2 0.25  OB 3 cos SBO   . SB 2   0 SBO  30 . c)
Tính khoảng cách từ điểm O đến mặt phẳng SBC, từ đó suy ra khoảng cách từ 1.0
điểm A đến mặt phẳng SBC. Kẻ OH  SM tại H . Ta có: O  H  SH  OH  BC 
vìBC  SOI   OH   OH  SBC 0.25  d O,  SBC   OH.  S . O OM a 10 OH   . 2 2 SO  OM 10 0.25 a Vậy d O  SBC 10 ,   .  10
Ta có: AC  2.OC  d  ,
A SBC   2.d O,SBC . 0.25 a  d  A SBC 10 ,  . 0.25 5 Câu 6
Cho lăng trụ đứng ABC.A' B 'C ' có đáy là tam giác vuông tại , B AC  5 , a (0,5 điểm) BC  3 ,
a góc giữa mặt phẳng  AB 'C ' mặt đáy bằng 0
45 .Tính độ dài đường cao của lăng trụ đã cho.
  AB 'C '  A' B 'C '  B 'C '.
 A' B '   A'B 'C ', A'B '  B 'C '.
AB '   AB 'C ', AB '  B 'C '  ì
v B 'C '   ABB ' A'  AB '  0.25  AB C   A B C       A B AB    0 ' ' , ' ' ' ' ', ' AB ' A'  45 . 2 2
A' B '  A'C '  B 'C '  4 . a 0 AA'  A ' B '.tan 45  4 . a 0.25
Vậy độ dài đường cao của lăng trụ đã cho bằng 4a.