SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ KIỂM TRA HỌC KỲ 2 THÀNH PHỐ HỒ CHÍ MINH (Năm học 2019 – 2020) TRƯỜNG THPT THĂNG LONG MÔN: TOÁN – KHỐI 11 (Đề chính thức)
Thời gian: 90 phút (không kể thời gian giao đề)
Họ tên học sinh: .................................................................................. Lớp: ............................ SBD: ............................
(Lưu ý: Học sinh làm bài trên giấy thi, không làm trên đề, không sử dụng tài liệu) Câu 1. (3.0 điểm) 2 4n  2n 2 x  5x  6 a) Tính giới hạn lim b) Tính giới hạn lim 2 1 3n x2 x  2 2  x  6x  8  khi x  4 
c) Xét tính liên tục của hàm số f  x   x  4 tại điểm x  4. 2x 6 khi x  4 
Câu 2. (3.0 điểm) Tính các đạo hàm sau a) y  x  x  3 4 2 3 1 b) 2 y  3x 2x . 2x 5
Câu 3. (1 điểm) Viết phương trình tiếp tuyến của đồ thị hàm số y  tại điểm M 1;  1 . x 4
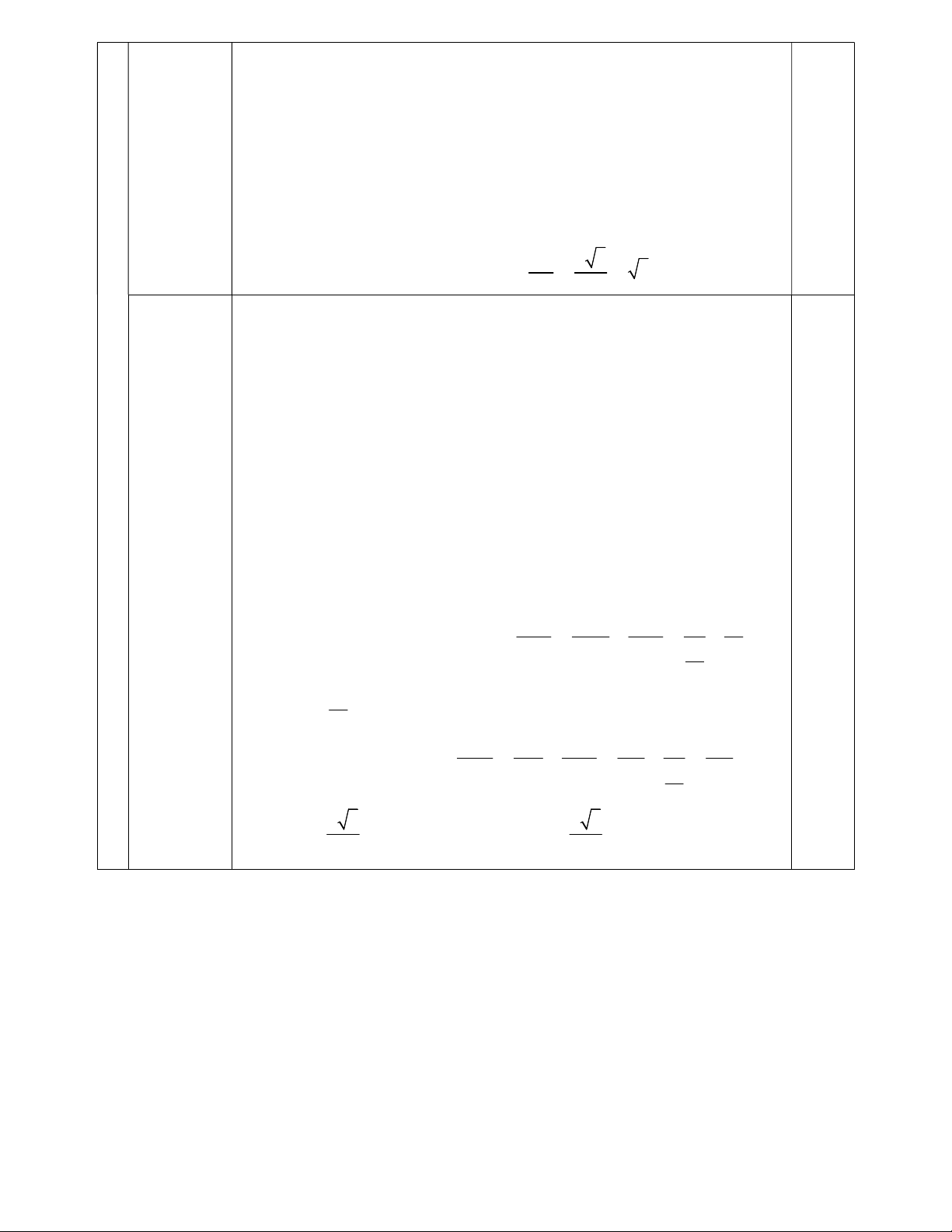
Câu 4. (3.0 điểm) Cho hình chóp S.ABCD 
có đáy ABCD là hình vuông cạnh a , SA a 3 và SA vuông góc
với mặt phẳng đáy  ABCD , M là trung điểm AB
a) Chứng minh BC  SAB
b) Tính góc hợp bởi đường thẳng SB và mặt phẳng SAD
c) Tính khoảng cách từ điểm A đến mặt phẳng SDM  . ------Hết------ TRƯỜNG THPT THĂNG LONG
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ II (NH 2019 – 2020) Môn: Toán – Khối 11 Câu Nội dung Điểm 1 a 2 4n 2n 2 1,0 (1 điểm) 2  4  2 2 4n  2n 4  lim  lim n n  lim n   2 2 1 3n 1 3n 1 3   3 2 2 2 n n n b 2 x  5x  6 x  2x 3 0,5x2 (1 điểm)  lim lim limx 3  1  x2 x2 x2 x  2 x  2 c  Khi x  4  thì 0,5 (1 điểm) 2  x  x   x  x  lim f  x 6 8  4 2  lim    lim
 lim x  2  2 x 4  x4 x4 x4  x  4  x  4  Khi x  4  thì f  4    2 4    6  2 
 Vì lim f  x  f 4  2 nên hàm số đã cho liên tục tại điểm x  4. x 4  0,5 2 a 2 4 2 4 2  2 4 2 3 (1,5 điểm)
 y  3x 3x  1 x 3x  1  3x 3x  1 4x 6x 1,5 b 2  (1,5 điểm) 3x 2x 6x 2 3x 1 1,5  y    2 2 2 2 3x 2x 2 3x 2x 3x 2x 3 (1 điểm) 3  y   y 1  1  2    0,5 x   4
 Phương trình tiếp tuyến tại M 1;  1 : y  
1 x  11 y x1 0,5 4 Vẽ hình S 0,25 H M A B K D C a
BC  AB Vì ABCD laø hình vuoâng (1 điểm)  BC  SA Vì SA   ABCD a.  Ta có:   BC  SAB. 1,0 S , A AB  SAB SA AB     A b
AB  AD Vì ABCD laø hình vuoâng (1 điểm)  AB  SA Vì SA  0,5  ABCD  Ta có:   AB  SAD tại A AD,SA  SAD  AD  SA     A
 Từ đó suy ra SA là hình chiếu vuông góc của SB lên mặt phẳng SAD 0,5
 Vậy SB SAD SB S   , , A  BSA SA a 3  Xét S  AB vuông tại A có   tan BSA    3  BSA  60 AB a c
 Từ A dựng AK  DM , dựng AH  SK , từ đó ta có: (0,75 điểm)
DM  AK Döïng hình  DM  SA Vì SA   ABCD   DM  SAK (1) AK,SA  SAK  0,25  AK  SA     A
AH  SK Döïng hình  AH  DM  chöùng minh (1)   Mặt khác   AH  SDM tại H SK,DM  SDM  SK DM   K  Từ đó suy ra d ; A SDM  AH 1 1 1 1 1 0,25
 Xét tam giác ADM vuông tại A có     2 2 2 2 2 AK AM AD a a 4 2 a 2  AK  5 1 1 1 1 1 16  Xét S  AK vuông tại A có      2 2 2 2 2 2 AH SA AK 3a a 3a 5 a 3 a  AH  . Vậy A SDM 3 d ;  AH  4 4 0,25
(Lưu ý: Học sinh làm cách khác và có bài làm đúng vẫn được điểm tối đa)