SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ II THÀNH PHỐ HỒ CHÍ MINH
LỚP 11- NĂM HỌC 2019-2020 TRƯỜNG THPT THANH ĐA Môn thi: TOÁN
Thời gian làm bài: 90 phút ĐỀ CHÍNH THỨC (Đề thi có 01 trang)
Câu 1 (2,0 điểm). Tính các giới hạn sau: 7x  5 2 2x  3x 1 2 a) lim b) lim c) lim x  x  3  x x   2 x 3x  2 x1 x 1  2 x  3x  4  khi x  4
Câu 2 (1,0 điểm). Cho hàm số f (x)   x  4
. Xét tính liên tục của  5 khi x  4 hàm số tại x  4 . 0
Câu 3 (3,0 điểm). Tính đạo hàm của các hàm số sau: 2 2x 1 a) y   3 x  2 6x  3 b) y  3 x 1 c) y  x   1 cosx d) y  2 tan 3x
Câu 4 (1,0 điểm). Cho hàm số y  f x   3 x  2 ( )
3x  4x  2 có đồ thị C . Viết phương
trình tiếp tuyến của C tại điểm có hoành độ bằng 2 .
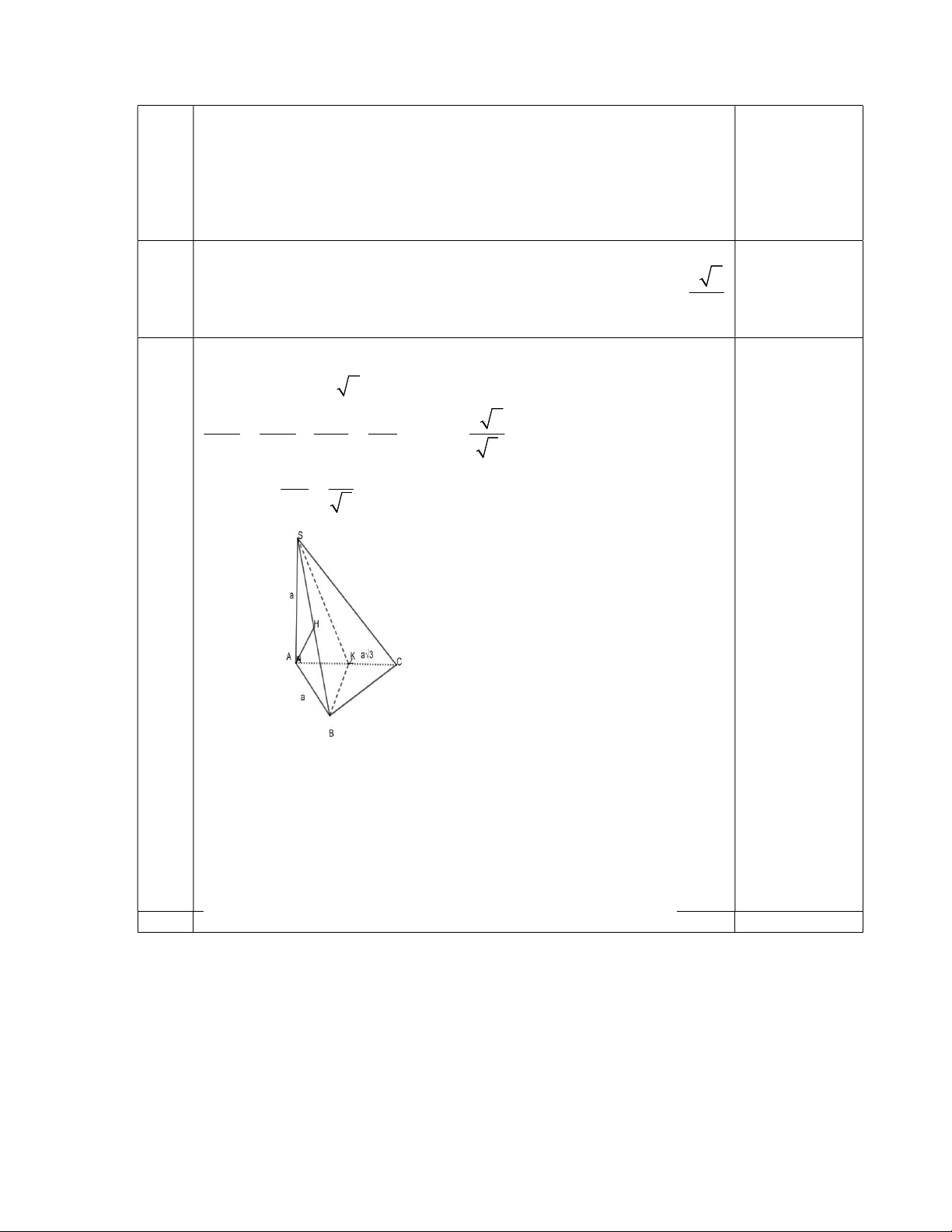
Câu 5 (3,0 điểm). Cho hình chóp S .ABC có đáy ABC là tam giác vuông tại B . Biết rằng
SA  (ABC), SA  a , AB  a , AC  a 3 . Dựng BK là đường cao của tam giác ABC .
a) Chứng minh BC  (SAB) , BK  SC .
b) Tính khoảng cách từ điểm A tới mặt phẳng (SBC) .
c) Xác định và tính góc tạo bởi SB và mặt phẳng (SAC). ----- Hết -------
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên thí sinh: …………………………………Số báo danh: ………………..........
Họ và tên giám thị: ….…………………………… .Chữ ký: ………………………….. ĐÁP ÁN Câu Đáp án Điểm Câu1  5  5 2đ x 7    7 7x  5   x  7 0,25+0,25 a) lim  lim  lim x  . x  3x  2 x   2  x  2 3 x 3  3   x    x 0,25+0,25+0,25 2 2x  3x 1 x  12x  1 2x 1 1 b) lim  lim   x  1  2  x  1 x 1  x  x   lim . 1 1 x  1  x 1 2 2 2  2 
( x  x  3  x )( x  x  3  x ) 0,25
lim  x  x  3  x  lim x   x  2   x  x  3  x c) 3 1   0,25+0,25 x  3 1  lim  lim x  . x  2 x  x  3 x  x  1 3 2  1   1 2 x x Câu2 f (4)  5 0,25 1đ x  1x  4 lim  x   0,25+0,25 x  x  4 lim  1 5 4 x 4
lim f (x )  f (4) nên hàm số liên tục tại x=4 0,25 x 4 Câu3 2 3 2 0.25+0,25+0,25 3đ a) 2
y   x  6x  3  y '  2x 12x 3 '  2x 1 0,25+0,5 2x 1   x   1  3 b) y   y '   . x 1 2x 1 2x 1 2 2 2(x 1) x 1 x 1 c) 0,25 y  x  
1 cosx  y '  x   1 'cosx  x   1 (cosx )' 0,5  cosx  x   1 sin x . y  2
tan 3x  y'  2 tan3x tan3x'  23x'tan3x 1 2 tan 3x 0,25+0,25+0,25 d) .  6 tan3x 1 2 tan 3x
Câu4 Pttt có dạng y  y '(x )(x  x )  y 1đ 0 0 0 0,25 2 y '  3  x  6x  4 0,25+0,25 y  2  ,y'(2)  4  0,25 0 Pttt y  4  x  6 Câu5 BC  AB (....) 0,25+0,25+0,25 3đ a)   BC  SAB BC  SA (....) 0,25+0,25+0,25 BK  AB (...)   BK  SC BK  SA (...) b) 0,25+025+0,25 a 2
vÏ AH  SB t¹i H .Cm ®­îc AH  (SBC)  d(A,(SBC))=AH= 2
c) SK lµ hcvg cña SB trªn SAC nªn SB,(SAC)   BSK 0,25 2 2 BC  2a ,SB  a 2, 0,25 1 1 1 3 a 2     BK  0,25 2 2 2 2 BK AB BC 2a 3  BK 1 sin BSC     0 BSC  35 ,26 SB 3