TRƯỜNG THPT THỦ ĐỨC
ĐỀ KIỂM TRA HỌC KỲ II - KHỐI 11 NĂM HỌC: 2019 - 2020
Môn: TOÁN - Thời gian: 90 phút. -------- ----------------- ĐỀ CHÍNH THỨC Câu 1. (2,0 điểm) Tính các giới hạn sau 2 2  x  x  6 2 2x  x  2x x  5 a) lim b) lim c) lim 2 x2 x  4 x x 1 x 2  2  x Câu 2. (1,0 điểm)  3  x  khi x  3
Xét tính liên tục của hàm số f  x   x 1  2 tại x  3. 0  4  khi x  3 Câu 3. (1,5 điểm)
Tính đạo hàm của các hàm số sau: 1 a) 4 y  mx  3m   2
1 x  2m 1 ( m là tham số) 4  π  b) 2 y  7x  5x  3 c) y  cos  3x  tan 2x    4  Câu 4. (1,5 điểm)
a) Viết phương trình tiếp tuyến của đồ thị hàm số y  f  x 3
 x  3x  2020 biết tiếp tuyến có hệ số góc k  9 .
b) Một vật chuyển động thẳng xác định bởi phương trình s t  1 3 2
  t  3t  2 trong đó t được tính bằng giây s và st 3
được tính bằng mét m . Tính vận tốc tức thời của vật khi gia tốc
của vật bị triệt tiêu. Câu 5. (1,0 điểm)
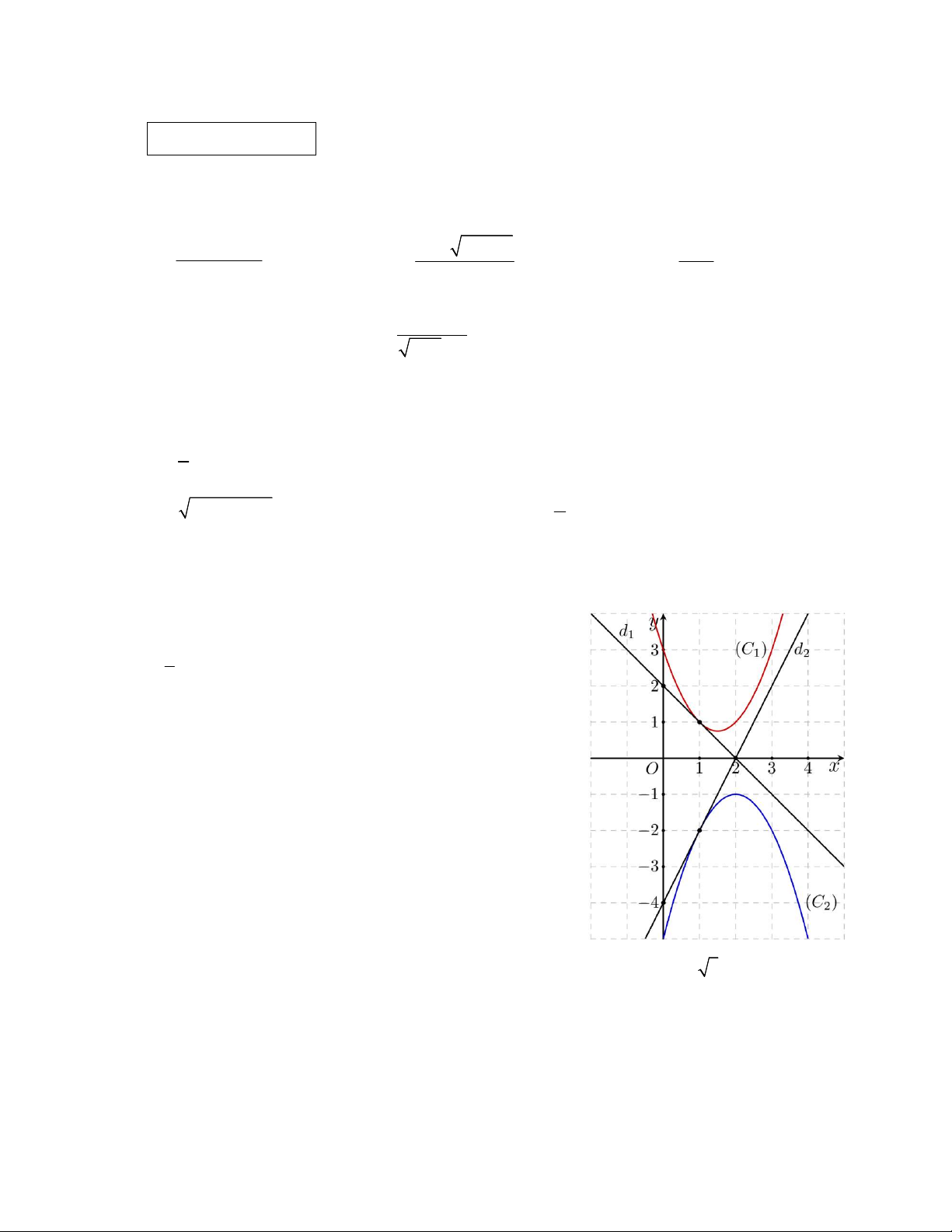
Cho hai hàm số y  f  x và g  x có đồ thị C và C như 2  1 
hình vẽ bên. Biết đường thẳng d , d lần lượt là tiếp tuyến của đồ 1 2
thị C và C tại điểm x  1. 2  1  0
a) Dựa vào đồ thị xác định f   1 và g  1 .
b) Gọi hàm số h  x  f  x.g  x . Tính h  1 . Câu 6. (3,0 điểm)
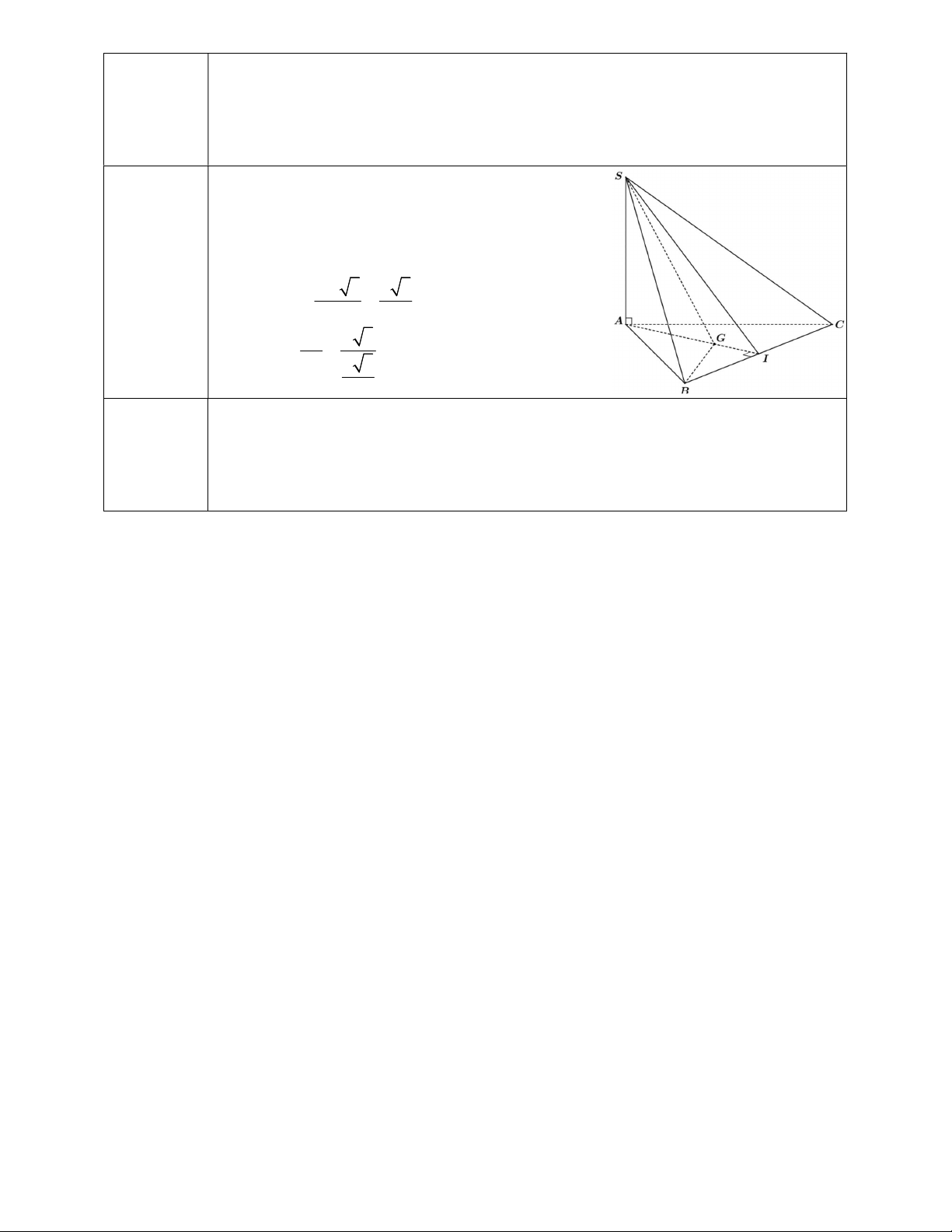
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bẳng a , cạnh SA  a 3 và SA   ABC .
Gọi I là trung điểm cạnh BC .
a) Chứng minh BC  SAI  .
b) Gọi  là góc giữa đường thẳng SI và mặt phẳng  ABC . Tính tan .
c) Gọi G là trọng tâm tam giác ABC . Chứng minh SBG  SAC. ------Hết------
ĐÁP ÁN ĐỀ KIỂM TRA MÔN TOÁN KHỐI 11 HỌC KỲ II – NĂM HỌC 2019 – 2020 Câu Nội dung 1a 2 2  x  x  6 x 2 2  x   3 2  x  3 7 lim  lim  lim   . 0,25đx3 (0,75 điểm) 2 x2 x  4 x2
x 2x  2 x2 x  2 4 2 2 2x  x 1 2  1 1b 2 2x  x  2x x  x   (0,75 điểm) lim lim lim 3 . 0,25đx3 x x 1 x x 1 x 1 1 x x  5  lim  x  5  3   0   x2  1c lim  x 2  2  x
vì lim 2  x  0 . 0,25đx2 (0,5 điểm) x2  x  2  2  x  0.   3  x  khi x  3
Xét tính liên tục của hàm số f  x   x 1  2 tại x  3. 0 4 khi x  3 2 + Ta có f 3  4  . 0,25đ (1,0 điểm) 3  x 3 x x1 2 + lim f  x  lim  lim  lim     . 0,25đx2   x 1 2 4 x 3  x 3  x 1  2 x3 x  3 x 3
+ Do lim f  x  f 3  4
 nên hàm số f  x liên tục tại x  3. 0,25đ x 3  0 3a 1 4 y  mx  3m   2 1 x  2m 1. 3 y  mx  23m   1 x . 0,5đ (0,5 điểm) 4  2 7x  5x  3 3b 14x  5 2
y  7x  5x  3 . y   . 0,25đx2 (0,5 điểm) 2 2 2 7x  5x  3 2 7x  5x  3 3c  π   π  2 y  cos 3x  tan 2x   . y  3  sin  3x    . 0,5đ (0,5 điểm)  4  2  4  cos 2x
Viết phương trình tiếp tuyến của đồ thị hàm số y  f  x 3
 x  3x  2020 biết tiếp
tuyến có hệ số góc k  9 .
+ Gọi M x ; y là tiếp điểm. Phương trình tiếp tuyến tại M có dạng 0 0  4a
 : y  yx x  x  y . 0   0  (0,75 điểm) 0
+ Ta có k  9  y x  2
 9  3x  3  9  x  2  . 0,25đ 0 0 0
 Với x  2  y  2022   : y  9(x  2)  2022  9x  2004 . 0,25đ 0 0
 Với x  2  y  2018   : y  9(x  2)  2018  9x  2036 . 0,25đ 0 0 1 + s t  3 2
  t  3t  2 , vt  st 2  t   6t . 0,25đ 4b 3
(0,75 điểm) + a t   vt   2  t  6 . 0,25đ + a  0  2
 t  6  0  t  3  v3  9 (m/s) 0,25đ a) f   1  1  , g  1  2 . 0,25đx2 5 (1,0 điểm) b) h  1  f   1 g   1  g  1 f   1  1  . 2
   2.1 4 . 0,25đx2
Chứng minh BC  SAI  . 6a BC  AI Ta có  0,25đx2 (1,0 điểm) BC  SA  BC  SAI  . 0,5đ
Tính góc giữa đường thẳng SI và mặt phẳng  ABC.
+ Ta có AI là hình chiếu vuông góc của SI trên mp
ABC SI,ABC    SIA . 0,25đ 6b (1,0 điểm) AB 3 a 3 + Ta có AI   . 0,25đ 2 2 SA a +  3 tan SIA    2 . 0,25đx2 AI a 3 2
Gọi G là trọng tâm tam giác ABC . Chứng minh SBG  SAC . 6c BG  AC Ta có   BG  SAC 0,25đx3 (1,0 điểm) BG  SA
 SBG  SAC . 0,25đ