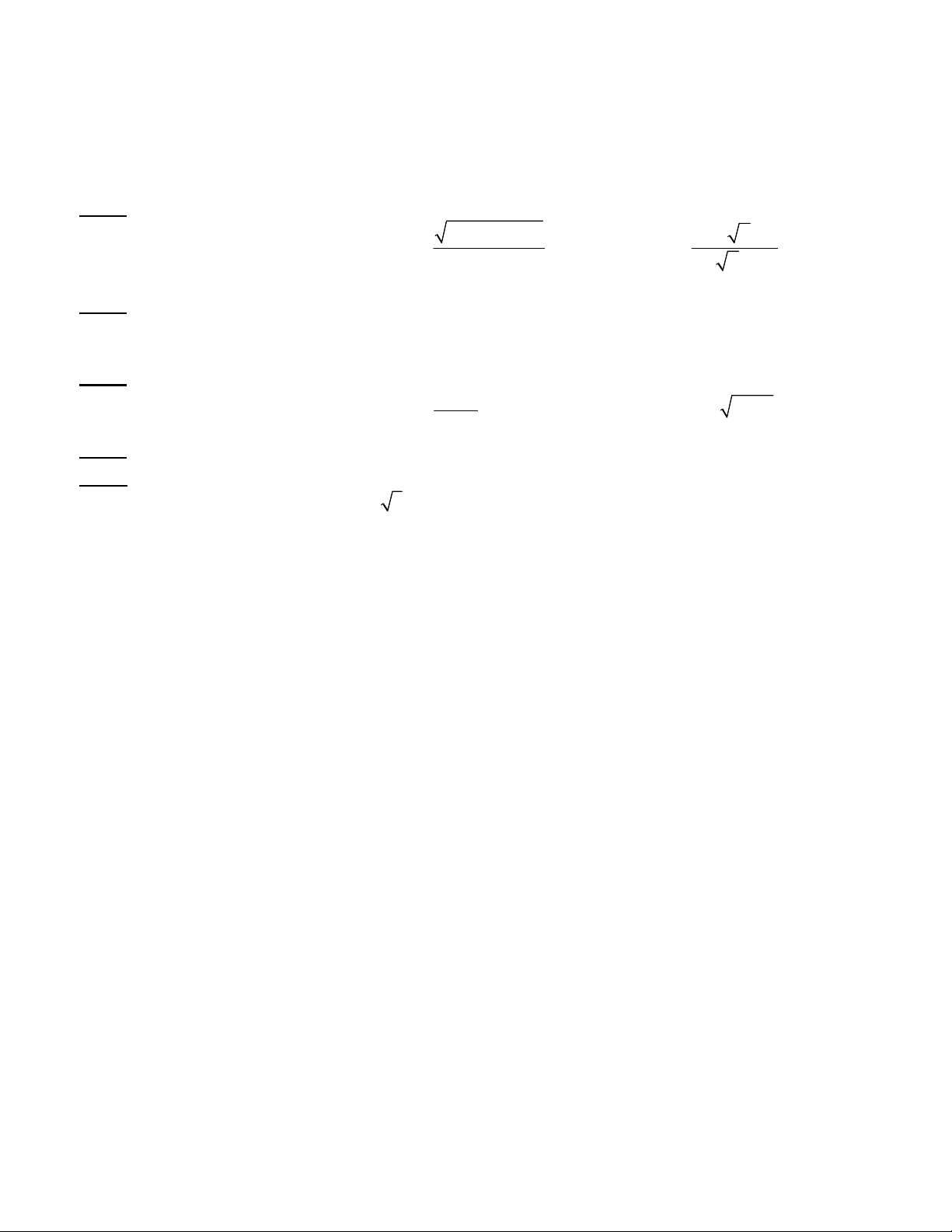
Preview text:
TRƯỜNG THPT TRƯNG VƯƠNG KIỂM TRA HỌC KÌ II NĂM HỌC 2019 - 2020 Môn: Toán - Khối 11 -----o0o-----
Thời gian làm bài: 90 phút
Họ tên học sinh : .......................................................... ..... Số báo danh :………………
Câu 1: (2,0 điểm) Tính các giới hạn sau: 2 2x 3x 10 x 3 x 2 a/ lim 3 2 x 3x 5 b/ lim c/ lim x 1 x 5x 2 x4 x x 8 2
x 5x 6 khi x 2
Câu 2: (1,0 điểm) Cho hàm số f (x) 2 m x 8 khi x 2
Tìm tất cả các giá trị của m để hàm số liên tục tại điểm x 2 . 0
Câu 3: (2,0 điểm) Tìm các đạo hàm của các hàm số sau: 2x 1 a/ 3 y x sin x 2 b/ y c/ 2 y tan x 1 x 3
Câu 4: (1,0 điểm) Viết phương trình tiếp tuyến với đồ thị (C) của hàm số 3
y x x 3 tại điểm A1; 1 .
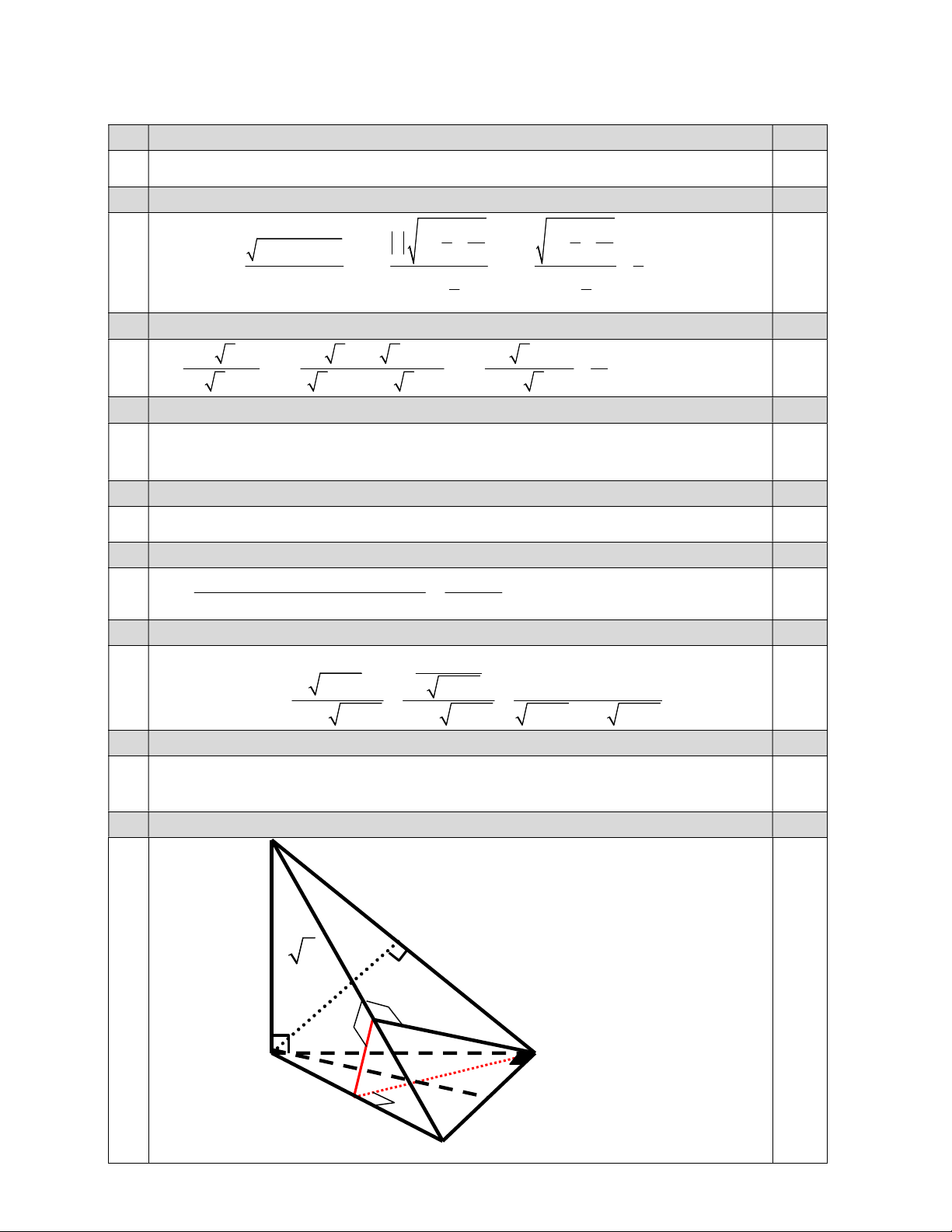
Câu 5: (4,0 điểm) Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B và BC a ; SA vuông
góc mặt phẳng ABC và SA a 3 .
a/ Chứng minh: BC SAB .
b/ Gọi M là trung điểm của đoạn AC. Chứng minh rằng SBM SAC .
c/ Tính góc giữa hai mặt phẳng SBC và SAC .
d/ Gọi G là trọng tâm tam giác ABC. Tính khoảng cách từ G đến mặt phẳng SBC . --- Hết --- TRƯỜNG THPT TRƯNG VƯƠNG
ĐÁP ÁN - KIỂM TRA HỌC KÌ II NĂM HỌC 2019 - 2020 Môn: Toán - Khối 11 -----o0o----- 1a 1 đ 3 2 3 2
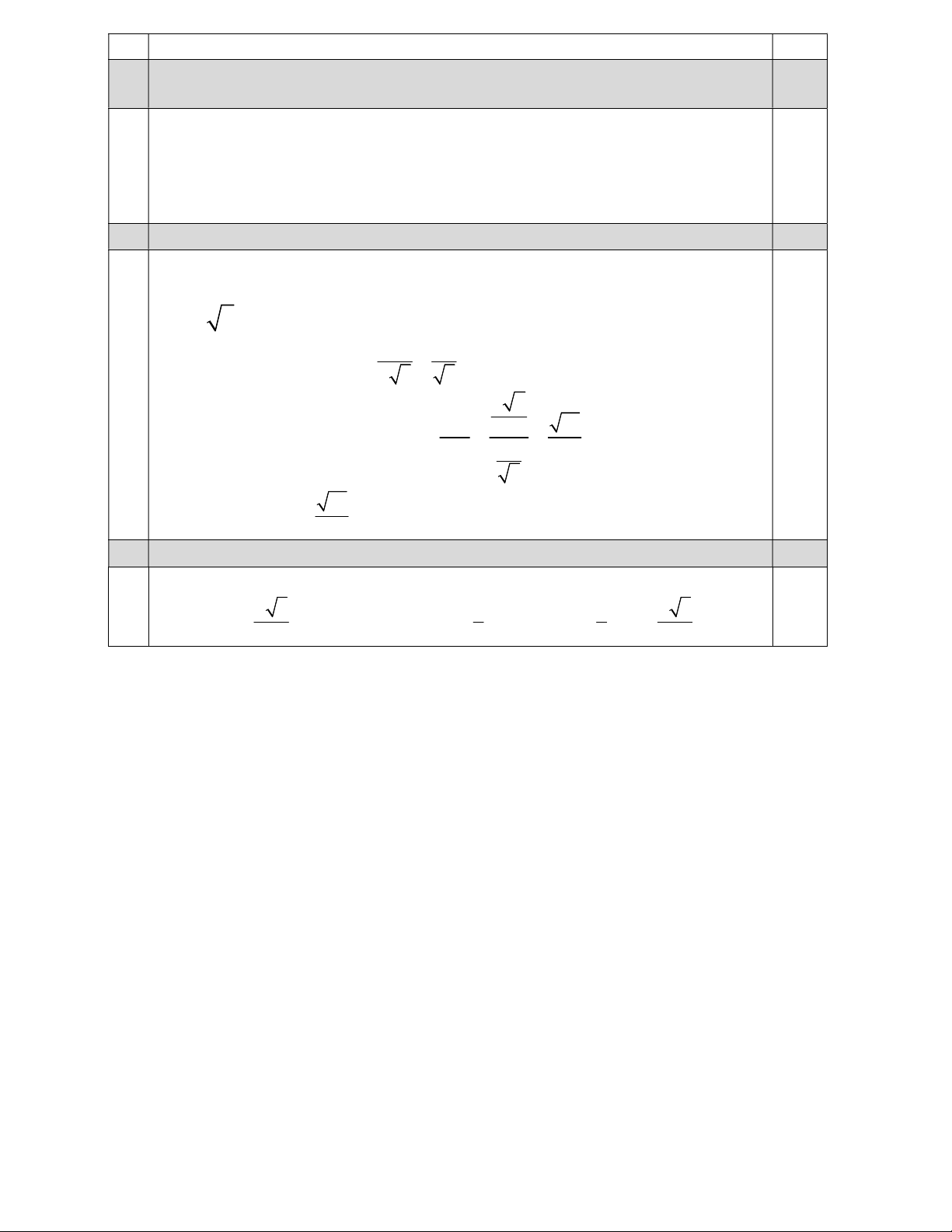
lim(x 3x 5) 1 3.1 5 3 x 1 1b 0.5 3 10 3 10 2 x 2 2 2 2 2x 3x10 x x x x 2 lim lim lim x 5x2 x 2 x 2 5 ( x 5 ) (5 ) x x 1c 0.5 x3 x 2 ( x 2)( x 1 ) ( x 1 ) 1 lim lim lim x 4 x 4 x 4 x x 8 ( x 2)(x2 x 4) (x2 x 4) 12 2 1 đ f (2) 0 và 2 2 lim(m x 8) 2m 8 . x2
Hàm số lt tại x=2 khi 2m28=0 m=2 3a 1 đ 2 y ' 3x cos x 3b 0.5
(2x 1) '(x 3) (x 3) '(2x 1) 7 y ' 2 2 (x 3) (x 3) 3c 0.5 2 (x 1) ' 2 2 ( x 1) ' 2 x 1 x y ' 2 2 2 2 2 2 2 cos x 1 cos x 1 x 1 cos x 1 4 1đ 2 y ' 3x 1 và y’(1)=4
suy ra pttt tại A là: y y '(1)(x 1) 1 4x 5 5a 1 đ S Chứng minh: BC (SAB). Ta có: 0.5 B C A B H B C (SA B ) 0.5 B C SA a 3 I a A B G a M A’ C
5b Chứng minh: (SBM) (SAC) 1đ Ta có: B C A C 0.5 B M (SA C ) B M SA 0.5
Mà BM(SBM) nên (SBM) (SAC)
5c Tính góc giữa mặt phẳng (SBC) và (SAC) 1đ
Trong mp(SAC) kẻ MI SA AC BI.
Nên góc của (SBC) và (SAC) là góc MIB . SC= a 5 0.5 2 . a a 2a Ta có: BI.SC=SB.BC BI= a 5 5 a 2 MB 10 Trong MBI vuông tại M. 2 sin MIB BI 2a 4 5 0.5 suy ra: 10 MIB arcsin 4
5d Tính khoảng cách từ trọng tâm G của ABC đến mặt phẳng (SBC). 1đ CM được d(A,(SBC))=AH. 0.5 Tính a 3 a AH Suy ra: 1 1 3 d (G,(SBC)) d ( , A (SBC)) AH (0.5) 2 3 3 6 0.5




