

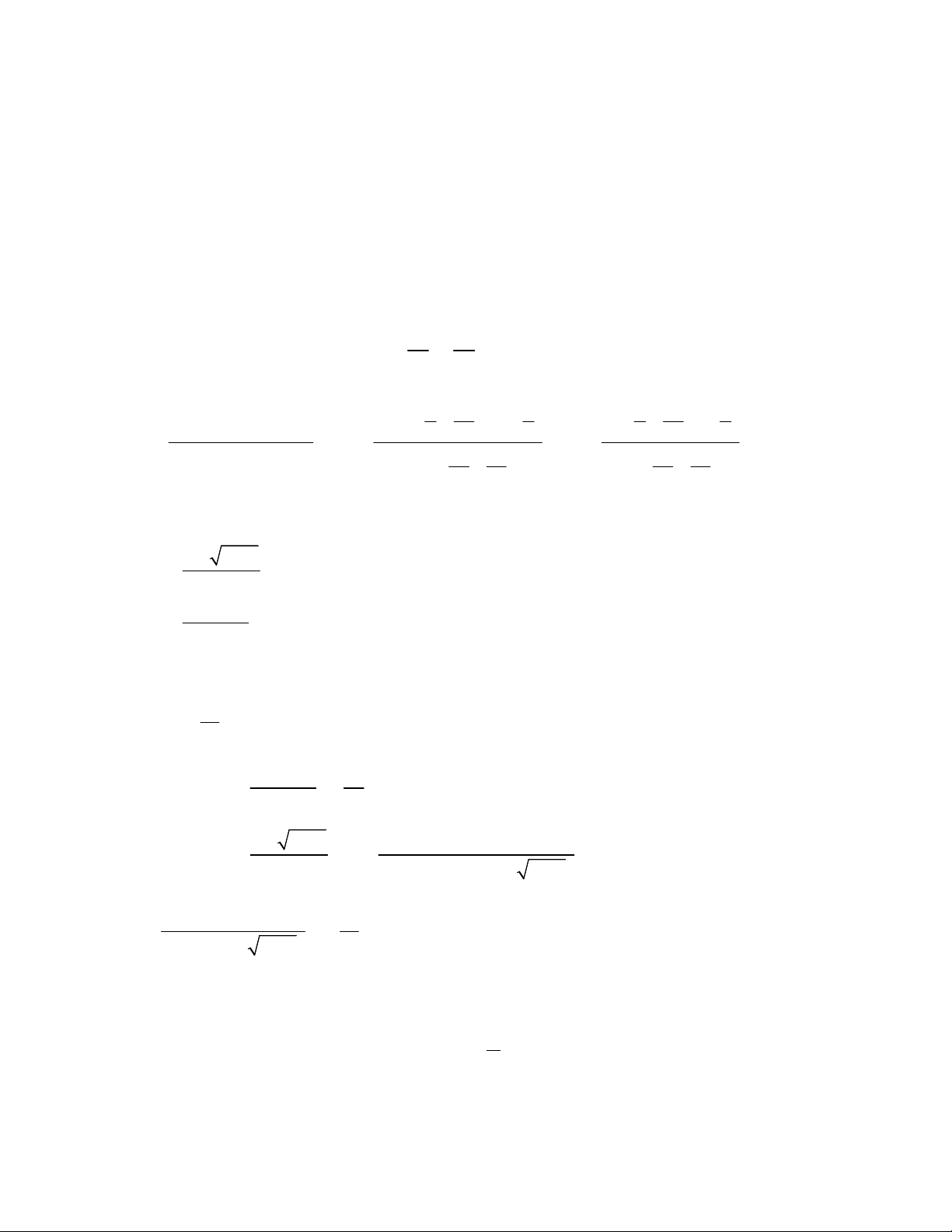


Preview text:
Sở Giáo dục – Đào tạo TP.HCM
ĐỀ KIỂM TRA HỌC KỲ II
Trường THPT Trường Chinh Năm học : 2019-2020 ( Đề có 02 trang ) Môn : Toán - Khối : 11 Thời gian : 90 phút Đề chính thức
Họ tên thí sinh ……………………………………….. SBD ……………………
Bài 1 (1,5đ) : Tính giới hạn sau: 2 (3x 7x 1)(x 2) a) lim 3 x 2x b) lim 1 x 3 x x 2x 1
Bài 2 (1đ) : Xét tính liên tục của hàm số sau tại điểm x = 2. 2 x 2 khi x 2 f x 2 x 4 2 x 2x khi x 2 128
Bài 3 (1đ) : Cho y 2 sin x cos 3x . Tính y ' 2
Bài 4 (1đ) : Cho hàm số y f x 3 2 x 3x 4
Tính f x và giải phương trình f x 0.
Bài 5 (1đ) : Viết phương trình tiếp tuyến với đồ thị y =
tại điểm có hoành độ bằng 1.
Bài 6 (1đ) : Viết phương trình tiếp tuyến của đồ thị H 1
: y biết tiếp tuyến song song với x đường thẳng d : y 4 x 7 .
Bài 7 (3đ) : Cho hình chóp SABCD, đáy ABCD là hình vuông tâm O. SB (ABCD) và
SD a 3, AB a , BM vuông góc SC tại M.
1) Chứng minh rằng (SAD) SAB và tam giác SCD là tam giác vuông.
2) Chứng minh rằng AM là đường cao của tam giác SAC.
3) Tính góc giữa hai mặt phẳng (SAD) và (ABCD) 1
Bài 8 (0,5đ) : Gọi k ,k lần lượt là hệ số góc của các tiếp tuyến với đồ thị 1 2 x 1 (C) : y
tại các điểm có hoành độ bằng x và x . Tìm m để k k đạt giá 2x 1 1 2 1 2
trị lớn nhất biết rằng x ,x là hai nghiệm của phương trình 2 2x 2mx m 1 0 1 2 Hết 2
Sở Giáo dục – Đào tạo TP.HCM
ĐÁP ÁN KIỂM TRA HỌC KỲ II
Trường THPT Trường Chinh Năm học : 2019-2020 Môn : Toán - Khối : 11 Thời gian : 90 phút Đề chính thức
Bài 1 ( 1,5 đ ) : Tìm các giới hạn sau: 2 1 a) lim 3 x 2x = 3 lim [x 1
] = –. 1 x 2 3 x x x 2 1 1 2 1 1 2 2 (3x 7x 1)(x 2) x (3 ) x(1 ) (3 )(1 ) 2 2 b) lim = x x lim x = x x lim x = 3. 3 x x 2x 1 x 3 2 1 x 2 1 x (1 ) 1 2 3 x x 2 3 x x
Bài 2 (1đ): Xét tính liên tục của hàm số sau tại điểm x = 2. 2 x 2 khi x 2 f x 2 x 4 2 x 2x khi x 2 128 Giải: + f 1 2 16 2 x 2x 1 + lim f x lim x 2 x 2 128 16 2 x 2 2 x + lim f x lim x x lim 2 2 2 x 4 x 2
x 2x 22 x 2 1 1 = lim = x 2
x 22 x 2 16
+ Kết luận: Hàm số liên tục tại x = 2.
Bài 3 (1đ) : Cho y 2 sin x cos 3x . Tính y ' 2 3 y ' 2 cosx 3 sin 3x y ' 3 2 Bài 4 (1đ) : 3 2 y x 3x 4 2 y 3x 6x y 2 0
3x 6x 0 0 x 2 Bài 5 (1đ) : y’ = , pttt y=-x+3 1 1 Bài 6 (1đ) : y ' . y '(x ) 4 x 2 x o o 2 1
x y 2 . Pttt: y = −4x + 4. 1 x y 2 . Pttt: y = −4x − 4. o 2 o o 2 o
Bài 7 (3đ): Cho hình chóp SABCD, đáy ABCD là hình vuông tâm O. SB (ABCD) và
SD a 3, AB a , BM vuông góc SC tại M.
a) Chứng minh rằng (SAD) SAB và tam giác SCD là tam giác vuông.
b) Chứng minh rằng AM là đường cao của tam giác SAC.
Tính góc giữa hai mặt phẳng (SAD) và (ABCD) a) AD AB(hv) AD SB(SB (ABCD)) AB,SB cat trong (SAB) AD (SAB) (SAD) (SAB) CD CB(hv) CD SB(SB (ABCD)) CB,SB cat trong (SAB) CD (SBC) CD SD SCD vuong b) 4 BA CB(hv) AB SB(SB (ABCD)) BC,SB cat trong (SBC) AB (SBC) AB SC ma BM SC SC (MAB) SA AM
AM la duong cao tam giac SAC c) AD AB(hv) AD SB(SB (ABCD)) AD (SAB) AD SA
(SAD);(ABCD) (S ; A AB) SAB BD a 2 SB a SB tan SAB 1 SAB 45 AB Bài 8 (0.5 đ): 1 1 2 2 k k
4m 8m 6 4(m 1) 2 1 2 2 2 (2x 1) (2x 1) 1 2
k k đạt GTLN khi m 1 1 2 5




