SỞ GIÁO DỤC VÀ ĐÀO TẠO KIỂM TRA HỌC KỲ 2 THÀNH PHỐ HỒ CHÍ MINH MÔN :TOÁN - KHỐI : 11
TRƯỜNG THPT VÕ VĂN KIỆT
Thời gian làm bài : 90 phút ĐỀ CHÍNH THỨC
Ngày kiểm tra : 23 /06 /2020
Câu 1: (2,0 điểm) Tính các giới hạn sau : 3 7n  2n 1 3 2x  x 1 a / lim b / lim 3 n  2n 2 x 1  2x  3x  5 2x  5  5x 1 c / lim d     2 / lim 4x x 2x x  x2 x  2 Câu 2: (2,0 điểm) 2  x  7x 12   a/ Cho hàm số khi x 3 f (x)   x  3
. Tìm m để hàm số liên tục tại x  3. 0 2 m khi x  3
b/ Chứng minh rằng phương trình:  2 m  m   7 5
5 x  x 1  0 luôn có nghiệm với mọi m  R . Câu 3: (2,5 điểm)
1/ Tính đạo hàm của các hàm số sau:  1 3 2 2x 3
a / y  x  3x  2x 1 b / y  c y   2 / 3x   1 2 x   1 d / y  x  x x  5x  4 2 x
2/ Cho hàm số y  f  x 3 2
 x  3x  2 có đồ thị là C .
Viết phương trình tiếp tuyến của C , biết tiếp tuyến này song song với đường thẳng (d) : y  3  x  7.
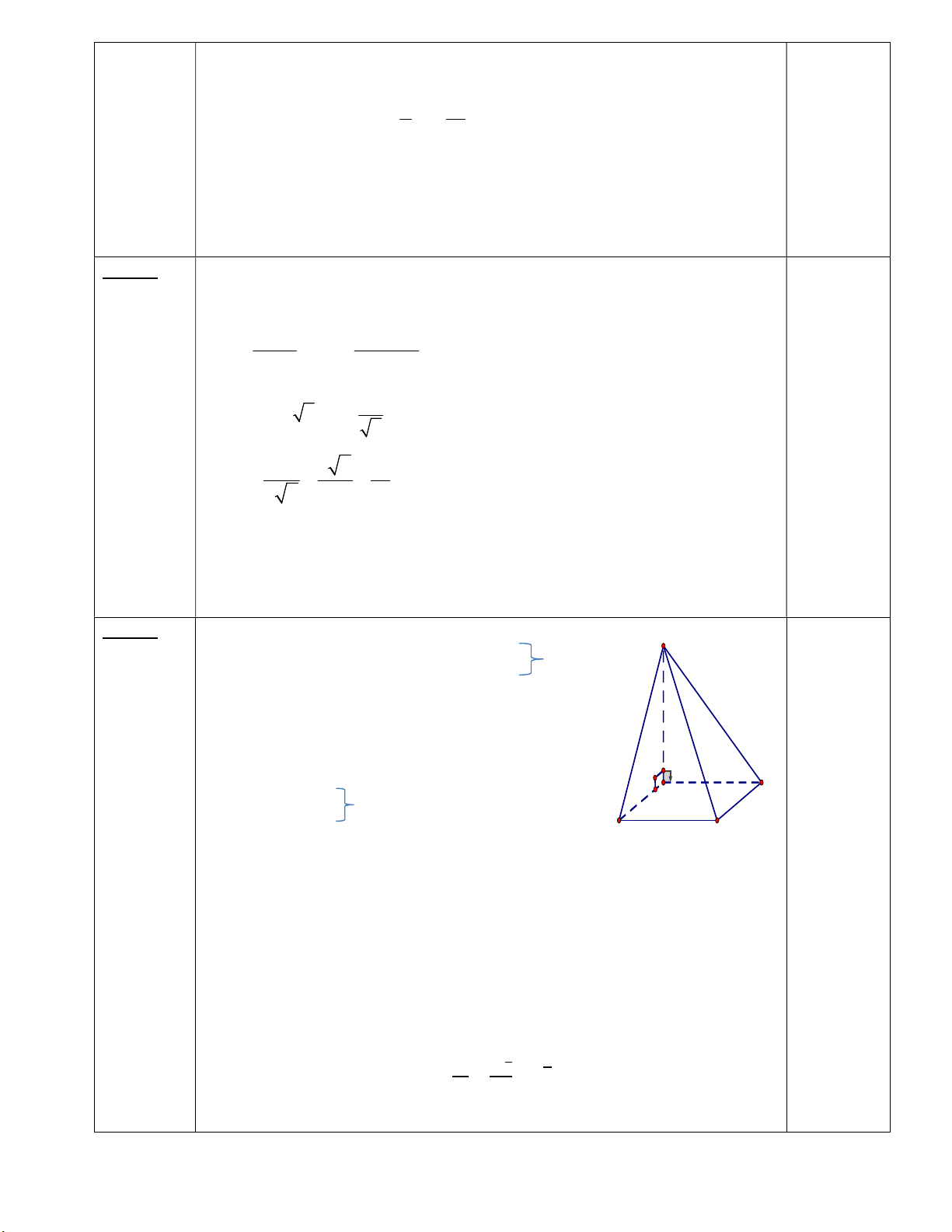
Câu 4: (2,5 điểm) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , 𝑆𝐴 ⊥ (𝐴𝐵𝐶𝐷) và 𝑆𝐴 = 𝑎√3
a/ Chứng minh: 𝑆𝐴 ⊥ 𝐶𝐷, 𝐵𝐶 ⊥ (𝑆𝐴𝐵)
b/ Chứng minh (𝑆𝐴𝐷) ⊥ (𝑆𝐷𝐶)
c/ Tính góc giữa SB và (ABCD)
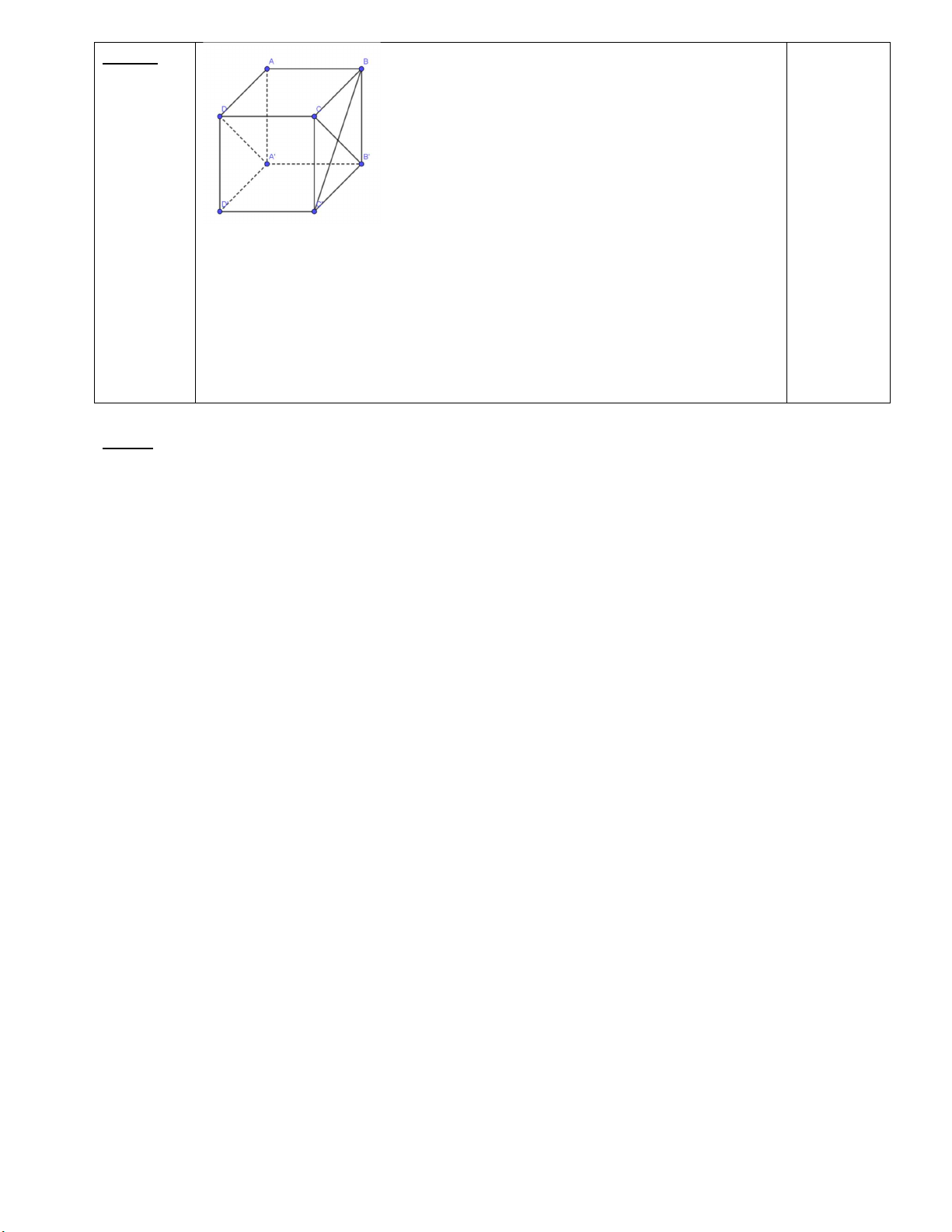
Câu 5: (1,0 điểm) Cho hình lập phương ABCD.A’B’C’D’. Chứng minh BC '   A' B'CD .
---------------------------------------------------------HẾT ----------------------------------------------------------
Lưu ý: 1/ Thí sinh được sử dụng máy tính có chức năng tương đương máy tính fx- 570VN-PLUS, fx- 580VNX,..
2/ Họ và tên thí sinh: Số báo danh: Lớp:
3/ Các em nhớ ghi lớp vào giấy làm bài.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ 2 – NĂM HỌC 2019 - 2020 THÀNH PHỐ HỒ CHÍ MINH MÔN: TOÁN - KHỐI: 11
TRƯỜNG THPT VÕ VĂN KIỆT
Thời gian làm bài: 90 phút
ĐÁP ÁN CỦA ĐỀ CHÍNH THỨC Ngày kiểm tra: 23/06/2020 NỘI DUNG ĐIỂM CÂU 1 2 1 3 7   (2,0 điểm) 2 3 7n  2n 1 / lim  lim n n a  7 0.25x2 3 n  2n 2 1 2 n 3 2 2x  x 1 2x  2x 1 5 b / lim  lim  0.25x2 2 x 1  x 1 2x  3x  5  2x  5 7 2x  5  5x 1 2x  5  5x 1 c / lim  lim 0.25x2 x2 x2 x  2
x  2 2x 5  5x 1 3 1  lim   x2 2x  5  5x 1 2 x  x  x x d x  x  x   0.25x2 x   2 2 2 4 4 / lim 4 2 lim lim x 2 4x  x  2 x x  1 x 4   2x x 1 1  lim  . x 1 4 4   2 x CÂU 2 a/ f (3)  2  m (2,0 điểm) 0.25x4 2 x  7x 12 x  4x 3 lim f (x)  lim  lim  lim(x  4)  1 x3 x3 x3 x3 x  3 x  3
Hàm số f (x) liên tục tại x  3 khi 2  m  1  m  3 . 0 b/ Xét f  x   2 m  m   7 5 5 x  x 1
Tập xác định: D = R  Hàm số liên tục trên R
 Hàm số liên tục trên 0;  1 0.25x4 Ta có: f 0  1 2   f   1 19 2 1  m  m  5  m    0 m   R    2  4  f 0. f   1  0
 Phương trình f x  0 có ít nhất một nghiệm 0;  1 CÂU 3 1/ (2,5 điểm) 2 a / y  3x  6x  2 0.25x2 2x  3 23 b / y   y '  0.25x2 5x  4 5x  42 c y  x  x   1 / ' 6 2 1   2 3x   1 0.25x2 x 1 3 x 2 d / y '    0.25x2 3 2 x 2 x
2/Gọi  là tiếp tuyến của (C) tại M (x , y ) . 0 0   d : y  3  x  7  f '(x )  3  2  3x  6x  3   x 1 y  0 . 0 0 0 0 0 0.25x2
Phương trình tiếp tuyến cần tìm là: y  3  (x 1)  0  y  3  x  3 (nhận). CÂU 4
a/ 𝑆𝐴 ⊥ (𝐴𝐵𝐶𝐷), 𝐶𝐷 ⊂ (𝐴𝐵𝐶𝐷) ⇒ 𝑆𝐴 ⊥ 𝐶𝐷 S (2,5 điểm) 0.25x4
𝑆𝐴 ⊥ (𝐴𝐵𝐶𝐷), 𝐵𝐶 ⊂ (𝐴𝐵𝐶𝐷) ⇒ 𝑆𝐴 ⊥ 𝐶𝐵
Mà 𝐶𝐵 ⊥ 𝐴𝐵 ( do ABCD là hình vuông )
⟹ 𝐶𝐵 ⊥ (𝑆𝐴𝐵)
b/ Có 𝐶𝐷 ⊥ 𝐴𝐷 ( do ABCD là hình vuông ) , 𝐶𝐷 ⊥ 𝑆𝐴 A B
⟹ 𝐶𝐷 ⊥ (𝑆𝐴𝐷) 0.25x4 D C
Mà 𝐶𝐷 ⊂ (𝑆𝐶𝐷) Vậy (SAD)  (SDC) c/ (SB,(ABCD))
Hình chiếu của SB trên (ABCD) là AB . 0.25x2
Nên (SB,(ABCD)) = (SB,AB) = 𝑆𝐵𝐴
Có 𝑆𝐴 ⊥ (𝐴𝐵𝐶𝐷), 𝐴𝐵 ⊂ (𝐴𝐵𝐶𝐷) ⇒ 𝑆𝐴 ⊥ 𝐴𝐵
Xét tam giác vuông SAB : 𝑡𝑎𝑛𝑆𝐵𝐴 =
= √ = √3 ⟹ 𝑆𝐵𝐴 = 60 CÂU 5 (1,0điểm) 0.5 Ta có
CD  BC (Do ABCD la hinh vuong)   CD  (BCC 'B ')
CD  CC ' (Do CDD 'C ' la hinh vuong)
BC '  B 'C (BCC 'B' la hinh vuong) 0.25x2 
BC '  CD' (Do CD '  (BCC 'B'), BC '  (BCC 'B'))  BC '  (A'B 'CD)
Lưu ý: Mọi cách làm khác nếu đúng giám khảo cho thang điểm tương ứng