4 trang 27 lượt tải

Đề thi học kì 2 Toán 11 năm 2019 – 2020 trường Trần Cao Vân – TP HCM

54

Giới thiệu đến quý thầy, cô giáo cùng các em học sinh lớp 11 đề thi học kì 2 Toán 11 năm học 2019 – 2020 trường THCS – THPT Trần Cao Vân, thành phố Hồ Chí Minh; đề thi có đáp án / lời giải chi tiết.

Chủ đề: Đề HK2 Toán 11 391 tài liệu

Môn: Toán 11 3.3 K tài liệu

Tác giả:

Profile

Kim Oanh

1 năm trước
Danh sách Quiz
/4
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THCS - THPT TRẦN CAO VÂN
(Đề thi gồm 01 trang)
ĐỀ THI KIỂM TRA HỌC KÌ II
NĂM HỌC 2019 - 2020
MÔN TOÁN - LỚP 11
Thời gian làm bài: 90 phút; không kể thời gian phát đ
ề
Họ, tên thí sinh: ......................................................Lớp: ...............SBD: ...............
Câu 1. (1,0 điểm) Cho cấp số cộng (u
n
) thỏa mãn
2 5
3 4
56
5 100
u u
u u
. Tìm số hạng đầu, công sai d
của (u
n
).
Câu 2. (1,0 điểm) Tìm số hạng đầu tiên, công bội của cấp số nhân biết
u u
u u
1 5
51
102
Câu 3. (1,0 điểm) Tìm giới hạn của dãy số:
2
2
4 2 3
lim
2 1
n n
n
Câu 4. (1,0 điểm) Tính
2
3
2
2
lim
6
x
x x
x x
Câu 5. (1,0 điểm) Tính đạo hàm hàm số sau:
3 2
1 1 3
8
3 2 2
y x x
x
Câu 6. (1,0 điểm) Tính đạo hàm hàm số sau:
cos 3sin 2 tan 7
y x x x
Câu 7. (1,0 điểm) Tính đạo hàm hàm số sau:
tan 2
y x x
Câu 8. (3,0 điểm) Cho hình chóp S.ABCD có đáy là hình vuông tâm O và SA vuông góc với
đáy. Biết
2 , 6
AB a SA a
a) Chứng minh CD vuông góc với mặt phẳng (SAD)
b) Tính góc giữa SO và mp(ABCD)
c) Tính khoảng cách từ O đến (SCD)
================== HẾT ==================
(Học sinh không được sử dụng tài liệu)
ĐÁP ÁN – THANG ĐIỂM (ĐỀ KIỂM TRA HỌC KÌ 2 – KHỐI 11)
CÂU ĐÁP ÁN ĐIỂM
1
Cho cấp số cộng (u
n
) thỏa mãn
2 5
3 4
56
5 100
u u
u u
. Tìm số hạng đầu, công sai d của (u
n
)
1
2 5
1
3 4 1
56
2 5 56
5 100 4 7 100
u u
u d
u u u d
0,25x2
1
18
4
u
d
0,25x2
2
Tìm số hạng đầu tiên, công bội của cấp số nhân biết
1 5
2 6
51
102
u u
u u
1
4
1 5 1 1
5
2 6
1 1
51 51
102
102
u u u u q
u u
u q u q
0,25
4
1
4
1
1 51 1
1 102 2
u q
u q q
0,25
Lấy (2) chia (1)
2
q
.
0,25
2
q
thế vào (1) suy ra
1
3
u
0,25
3
Tìm giới hạn của dãy số:
2
2
4 2 3
lim
2 1
n n
n
1
2
2
2
2
2
2
2 3
4 )
4 2 3
lim lim
1
2 1
n (2 )
n
n n
n n
n
n
0,25x2
2
2
2 3
4
4
lim 2
1
2
2
n n
n
0,25x2
4
Tính
2
3
2
2
lim
6
x
x x
x x
1
2
3 2
2 2
2 ( 2)( 1)
lim lim
6 ( 2)( 2 3)
x x
x x x x
x x x x x
0,25x2
2
2
1 3
lim
2 3 11
x
x
x x
0,25x2
5
Tính đạo hàm hàm số sau:
3 2
1 1 3
y x x 8
3 2 2x
1
'
' 3 2 2
2
1 1 3 1 1 3
y x x 8 .3x .2.x
3 2 2x 3 2 2x
(mỗi ý đúng được 0,25đ)
0,25x3
2
2
3
x x
2x
0,25
6
Tính đạo hàm hàm số sau:
cos 3sin 2 tan 7
y x x x
1
/ / / /
/
cos 3sin 2tan 7
y x x x
0,25
2
2
sin 3cos
cos
x x
x
(mỗi ý đúng được 0,25đ)
0,25x3
7 Tính đạo hàm hàm số sau:
y x tan 2x
1
' '
y (x tan 2x) (x)'.tan 2x x.(tan 2x)'
0,25x2
2
2x
tan 2x
cos 2x
0,25x2
8
Cho hình chóp S.ABCD có đáy là hình vuông tâm O và SA vuông góc với đáy. Biết
2 , 6
AB a SA a
a. Chứng minh CD vuông góc với mp(SAD)
b. Tính góc giữa SO và mp(ABCD)
c. Tính khoảng cách từ O đến (SCD)
3
a
Vẽ đúng dáng hình chóp theo đề bài được 0,25 (các đường phụ trong quá trình làm bài thì
không tính)
0,25
a. Chứng minh CD vuông góc với mp(SAD)
là hình vuông
CD AD ABCD
CD SA SA ABCD
CD SAD
0,25
0,25
0,25
b. Tính góc giữa SO và mp(ABCD)
Ta có :
SA ABCD
SO ABCD O
Suy ra OA là hình chiếu của SO lên mặt phẳng (ABCD)
0,25
0,25
O
I
H
C
D
B
A
S
,
SO ABCD SOA
Xét ABC vuông tại B ta có:
2 2
2 2
2 2 2 2 2
AC AB BC a a a OA a
Xét SAO vuông tại A ta có:
6
tan 3, 60
2
SA a
SOA SOA
OA
a
, 60
SO ABCD
0,25
0,25
c. Tính khoảng cách từ O đến (SCD)
Từ A kẻ AH vuông góc SD ta có:
AH SD gt
AH CD CD SAD AH
AH SCD
d( A,( SCD )) AH
Xét SAD vuông tại A ta có:
2 2 2 2
1 1 1 5 2 15 2 15
(A,(SCD))
12 5 5
a a
AH d
AH SA AD a
Ta có : O là trung điểm AC mà
2
d A, SCD
AH AC
AC SCD C
OI OCd O, SCD
1 15
2 5
a
d O, SCD d A, SCD
0,25
0,25
0,25
0,25
LƯU Ý: Học sinh làm cách khác mà đúng vẫn đạt điểm tối đa.
Kính nhờ quý thầy cô vui lòng chấm chi tiết và theo đúng thang điểm của đáp án.

Tài liệu khác của Toán 11

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI KIỂM TRA HỌC KÌ II THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2019 - 2020
TRƯỜNG THCS - THPT TRẦN CAO VÂN MÔN TOÁN - LỚP 11
Thời gian làm bài: 90 phút; không kể thời gian phát đề (Đề thi gồm 01 trang)
Họ, tên thí sinh: ......................................................Lớp: ...............SBD: ............... u   u  56
Câu 1. (1,0 điểm) Cho cấp số cộng (un) thỏa mãn 2 5 
. Tìm số hạng đầu, công sai d 5  3 u  u4 100 của (un). u1  u5  51
Câu 2. (1,0 điểm) Tìm số hạng đầu tiên, công bội của cấp số nhân biết    u2  u6   102 2 4n  2n  3
Câu 3. (1,0 điểm) Tìm giới hạn của dãy số: lim 2 2n 1 2 x  x  2
Câu 4. (1,0 điểm) Tính lim 3 x2 x  x  6 1 1 3
Câu 5. (1,0 điểm) Tính đạo hàm hàm số sau: 3 2 y  x  x   8 3 2 2x
Câu 6. (1,0 điểm) Tính đạo hàm hàm số sau: y  cos x  3sin x  2 tan x  7
Câu 7. (1,0 điểm) Tính đạo hàm hàm số sau: y  x tan 2x
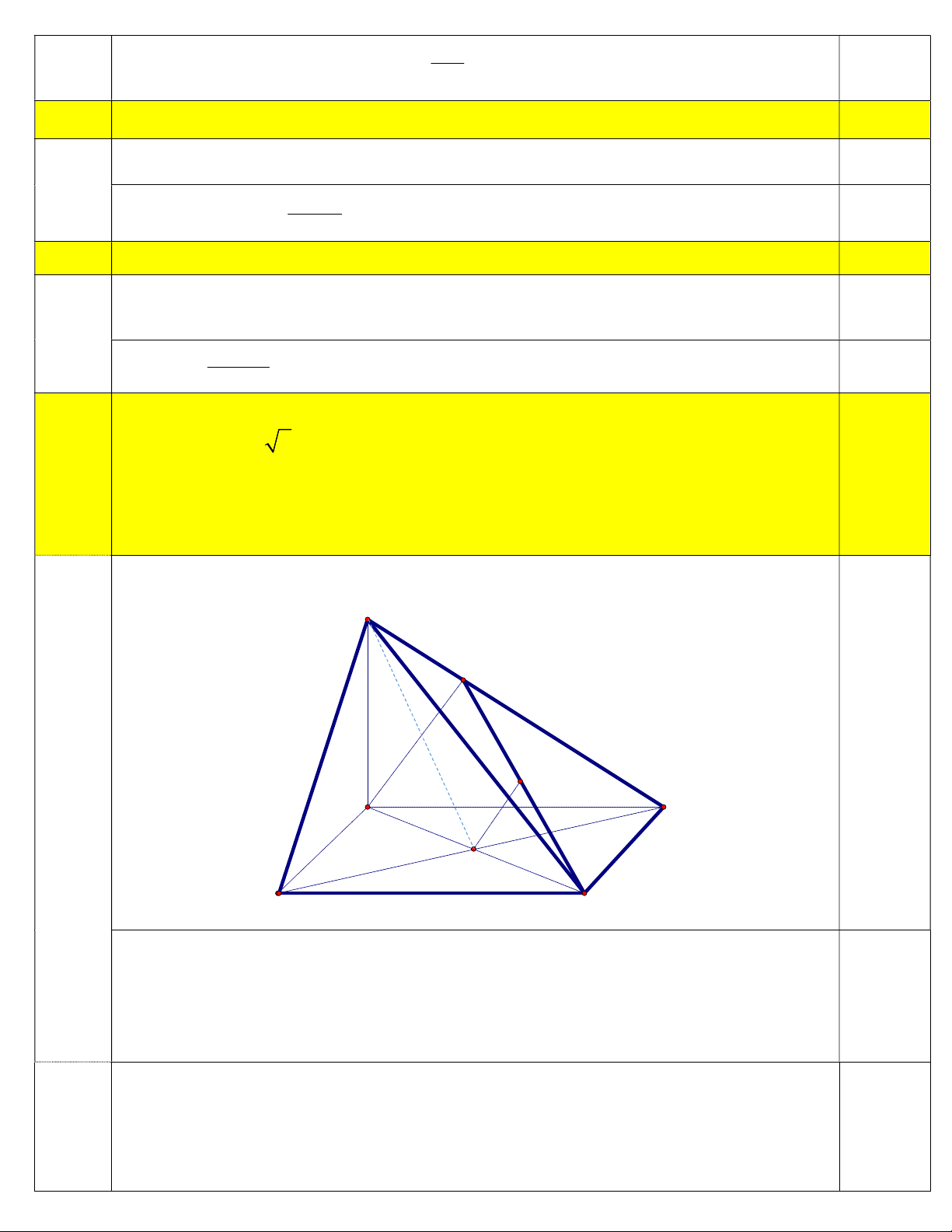
Câu 8. (3,0 điểm) Cho hình chóp S.ABCD có đáy là hình vuông tâm O và SA vuông góc với
đáy. Biết AB  2a, SA  a 6 a)
Chứng minh CD vuông góc với mặt phẳng (SAD) b)
Tính góc giữa SO và mp(ABCD) c)
Tính khoảng cách từ O đến (SCD)
================== HẾT ==================
(Học sinh không được sử dụng tài liệu)
ĐÁP ÁN – THANG ĐIỂM (ĐỀ KIỂM TRA HỌC KÌ 2 – KHỐI 11) CÂU ĐÁP ÁN ĐIỂM u   u  56 1
Cho cấp số cộng (un) thỏa mãn 2 5 
. Tìm số hạng đầu, công sai d của (un) 1 5u  3  u4  100 u  2  5 u  56 2 1 u  5d  56    0,25x2 5u  u  100 4u 7d  100  3 4  1 u   1 18   0,25x2 d  4 u   u  51 2
Tìm số hạng đầu tiên, công bội của cấp số nhân biết  1 5 u  u  102 1  2 6  4 u   u  51 u  u q  51  1 5  1 1    0,25 5 u   u  102   2 6 u q  u q  102   1 1  u   4 1 q  51 1 1      0,25 u  q   4 1 q  102 2 1   
Lấy (2) chia (1)  q  2 . 0,25
 q  2 thế vào (1) suy ra 1 u  3 0,25 2 3 4n  2n  3
Tìm giới hạn của dãy số: lim 1 2 2n 1 2 2 3 2 n 4   ) 2 4n  2n  3 lim  lim n n 0,25x2 2 2n 1 2 1 n (2  ) 2 n 2 3 4   2 4  lim n n   2 1 0,25x2 2 2  2 n 2 4 x  x  2 Tính lim 1 3 x2 x  x  6 2 x  x  2 (x  2)(x 1) lim  lim 0,25x2 3 2 x2 x2 x  x  6 (x  2)(x  2x  3) x 1 3  lim  0,25x2 2  x 2 x  2x  3 11 5 1 1 3
Tính đạo hàm hàm số sau: 3 2 y  x  x   8 1 3 2 2x ' '  1 3 1 2 3  1 2 1 3 y  x  x   8  .3x  .2.x   
(mỗi ý đúng được 0,25đ) 0,25x3 2  3 2 2x  3 2 2x 3 2  x  x  0,25 2 2x 6
Tính đạo hàm hàm số sau: y  cos x  3sin x  2 tan x  7 1 y   x/   x/   x/   / / cos 3sin 2tan 7 0,25 2  sin x  3cos x 
(mỗi ý đúng được 0,25đ) 0,25x3 2 cos x 7
Tính đạo hàm hàm số sau: y  x tan 2x 1 ' '
y  (x tan 2x)  (x) '.tan 2x  x.(tan 2x) ' 0,25x2 2x  tan 2x  0,25x2 2 cos 2x
Cho hình chóp S.ABCD có đáy là hình vuông tâm O và SA vuông góc với đáy. Biết AB  2a, SA  a 6 8 3
a. Chứng minh CD vuông góc với mp(SAD)
b. Tính góc giữa SO và mp(ABCD)
c. Tính khoảng cách từ O đến (SCD)
Vẽ đúng dáng hình chóp theo đề bài được 0,25 (các đường phụ trong quá trình làm bài thì không tính) S H 0,25 I a A D O B C
a. Chứng minh CD vuông góc với mp(SAD)
CD  AD  ABCD là hình vuông 0,25 
CD  SA SA   ABCD  0,25  CD  SAD 0,25
b. Tính góc giữa SO và mp(ABCD) 0,25 SA    ABCD
Ta có : SOABCD     O 0,25
Suy ra OA là hình chiếu của SO lên mặt phẳng (ABCD)
 SO, ABCD  S  OA 0,25
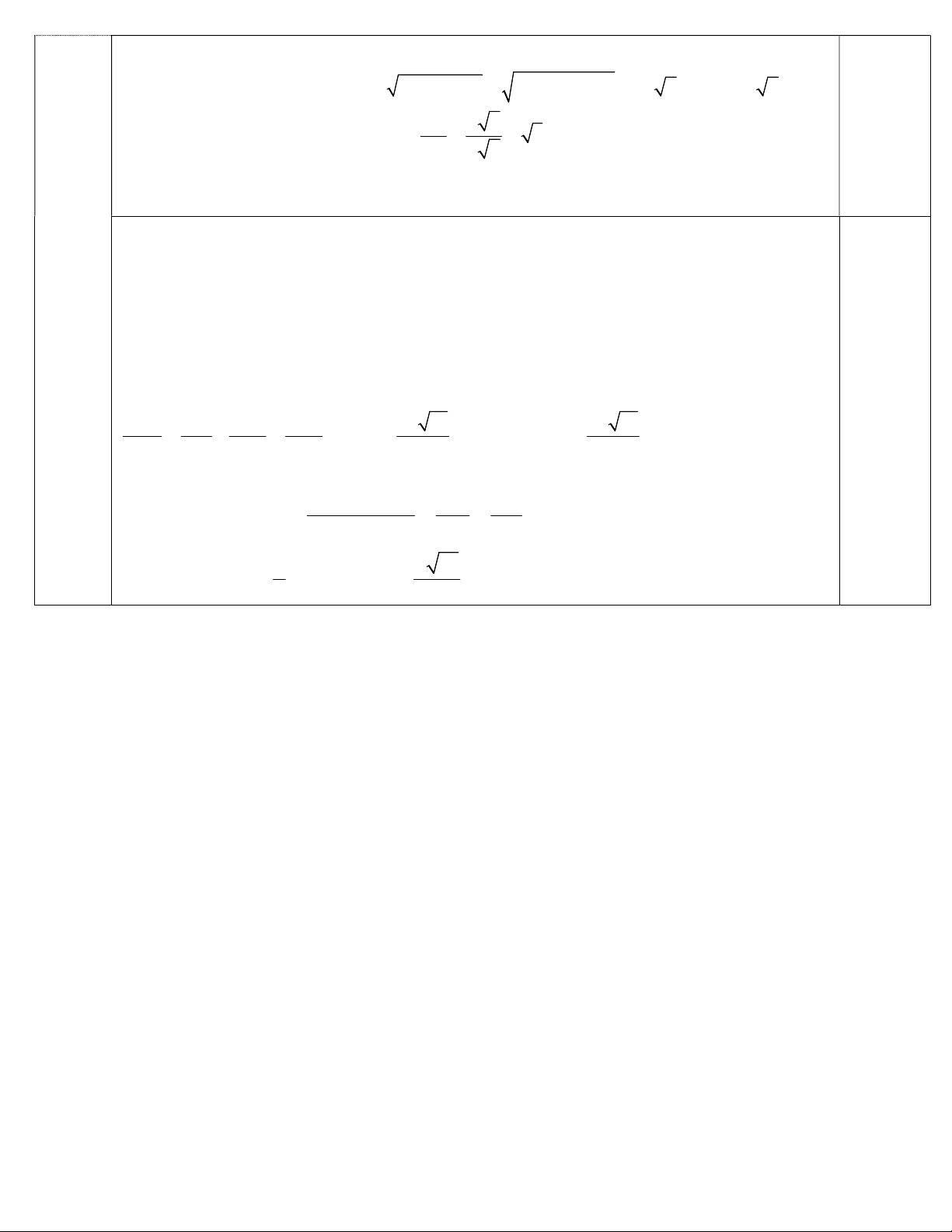
Xét ABC vuông tại B ta có: AC  AB  BC   a2   a2 2 2 2 2  2a 2  OA  a 2 0,25 SA a 6
Xét SAO vuông tại A ta có: tan SOA    3, S  OA  60 OA a 2
 SO, ABCD  60
c. Tính khoảng cách từ O đến (SCD)
Từ A kẻ AH vuông góc SD ta có: AH  SDgt
AH  CD CD  SAD AH 0,25  AH  SCD d( A,( SCD ))  AH 0,25
Xét SAD vuông tại A ta có: 1 1 1 5 2a 15 2a 15     AH   d(A,(SCD))  2 2 2 2 0,25 AH SA AD 12a 5 5
Ta có : O là trung điểm AC mà d  A, SCD          AH AC 0,25 AC SCD C     d O,SCD 2 OI OC  d O ,SCD 1  d  A,SCD a 15  2 5 LƯU Ý:
Học sinh làm cách khác mà đúng vẫn đạt điểm tối đa.
Kính nhờ quý thầy cô vui lòng chấm chi tiết và theo đúng thang điểm của đáp án.

Tài liệu liên quan: