SỞ GD & ĐT TP. HỒ CHÍ MINH Trường TH, THCS và THPT
ĐỀ KIỂM TRA HỌC KỲ II ( 2019 – 2020 ) TRƯƠNG VĨNH KÝ Môn: TOÁN – Khối: 11
Thời gian làm bài: 90 phút (Đề gồm 01 trang)
(Học sinh không được sử dụng tài liệu) Mã đề: A
Họ và tên học sinh: ............................................................................................................... Lớp: .........................
Số báo danh: .................................. Chữ ký học sinh: .......................................................... Ngày: 16/ 06/ 2020
Bài 1: (2 điểm). Tính đạo hàm các hàm số: 2x 1 a.) 3 2
y  2x  5x  4x  3 b.) y  x  3 c.) 2
y  3x  4x 1 d.) y  sin 3x  3cos(3  x) 2 3x  5x  2  (khi x  2)
Bài 2: (1 điểm). Xét tính liên tục của hàm số: y  f (x)   x  2 tại điểm x  2 . 0 4x 1 (khi x  2) Bài 3: (2 điểm).
a.) Viết phương trình tiếp tuyến của đồ thị (C) hàm số: 4 2
y  x  3x  2 tại điểm thuộc đồ thị có hoành độ x  2 . 0 x 1
b.) Viết phương trình tiếp tuyến của đồ thị (C) hàm số: y  f (x) 
. Biết rằng tiếp tuyến song song x 1
với đường thẳng (d): y  2x  4 .
Bài 4 : (1 điểm). Cho hàm số f (x)  2x x 1 . Giải phương trình : 2. f  (  x)  3x  2 .
Bài 5: (1 điểm). Cho hàm số 3 2 2
y  f (x)  x  3mx  (2m 1)x  2m  3 có đồ thị là (C ) . Gọi k là hệ số góc m 1
của tiếp tuyến của đồ thị tại điểm có hoành độ bằng –1, gọi k là hệ số góc của tiếp tuyến của đồ thị tại 2
điểm có hoành độ bằng 0. Tìm m để tổng k  k đạt giá trị nhỏ nhất. 1 2
Bài 6: (3 điểm). Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh 2a và có tâm O. Cạnh bên
SA  a 2 và vuông góc mặt đáy (ABCD) .
a.) Chứng minh: CD  (SAD) .
b.) Chứng minh hai mặt phẳng (SAC) và (SBD) vuông góc với nhau.
c.) Tính số đo của góc hợp bởi đường thẳng SO và mặt đáy (ABCD).
d.) Tính khoảng cách giữa hai đường thẳng SO và BM , với M là trung điểm SC.
----------------------- HẾT -----------------------
ĐÁP ÁN TOÁN 11 – KIỂM TRA HỌC KÌ 2 – 2019-2020 – ĐỀ A 1 a Tính đạo hàm a) 3 2 y  2x  5x  4x  3 / 2
y  6x 10x  4 ( đúng 2 số 0.25 ) 0.5 1 b 2x 1 Tính đạo hàm : y  x  3 2x  /
1 x  3   x  3/ 2x 1 0.25 /   y  x  32 0.25
2 x  3 12x   1 7 = 
(HS tính nhanh kq cho đủ điểm ) x 32 x 32 1 c Tính đạo hàm 2 y  3x  4x 1 3x 4x  / 2 1 3x  2 / y   0.25x 2 2 2 3x  4x 1 3x  4x 1 2 1 d
Tính đạo hàm y  sin 3x  3cos 3 x y   x/ x    x/ / 3 cos3 3 3
sin 3 x  3cos3x  3sin 3 x 0.25x 2 2 3x 5x  2 2  khi x  2
Xét tính liên tục y  f  x     x  2 tại điểm x  2 0 4x 1  khi x  2 * f(2) = 7 (1) 0.25
* lim f  x  lim 4x   1  7 (2) 0.25 x 2 x 2   2 3x  5x  2 * lim f  x  lim  lim 3x   1  7 (3) 0.25 x 2 x 2  x 2 x 2     0.25
Từ (1) , (2) , (3) suy ra hàm số liên tục tại x  2 0 3 a
Viết phương trình tiếp tuyến của đồ thị ( C) hàm số : 4 2
y  x  3x  2 tại điểm thuộc đồ thị có hoành độ x  2 0 * / 3 y  4x  6x 0.25 * Hệ số góc k = 20 0.25 * Tiếp điểm 2;6 0.25 0.25
PT Tiếp tuyến : y  6  20 x  2  y  20x  34 3 b x 
Viết phương trình tiếp tuyến của đồ thị ( C) hàm số : y  f  x 1 
.Biết rằng tiếp tuyến x 1
song song với đường thẳng (d) : y  2x  4 2 0.25 * y  x  2 1 2 x  2
*Hệ số góc tiếp tuyến k 0 0.25 tt = kd = - 2   2     x  2 1 x  0  0 0 0.25
*Tiếp điểm (2;3)  PT Tiếp tuyến : y = -2x +7 0.25
*Tiếp điểm ( 0 ;-1)  PT Tiếp tuyến : y = - 2x -1 4
Cho hàm số f  x  2x x 1 . Giải phương trình : // 2. f  x  3x  2     x  0.25 f x
2x x 1   x 1/ / 3 2 / 2x  x 1  0.25 3x  2 x 1  x 1 3x  2 3x  2 //  / /   f  x   x 1 2 x 13 0.25 3  x 2  0 3x  2 // 2.f x  3x 2  2.      ,điều kiện x > -1   3x 2  x x   3 3 1 1 2 1 0.25  2 x   (nh)   3  x  0 (nh) 5
Gọi k là hệ số góc của tiếp tuyến của đồ thị tai điểm có hoành độ bằng -1, k là hệ số góc 1 2
của tiếp tuyến của đồ thị tại điểm có hoành độ bằng 0.Tìm m để tổng k  k đạt giá trị nhỏ 1 2 nhất ? / 2 2
y  3x  6mx  2m 1 0.25 Ta có: 2 k  f '( 1  )  2m  6m  4 0.25 1 2 k  f '(0)  2m 1 2 2  3  29 29 0.25 Ta có 2
k  k  4m  6m  5  4 m     1 2    4  4 4 0,25 29 3
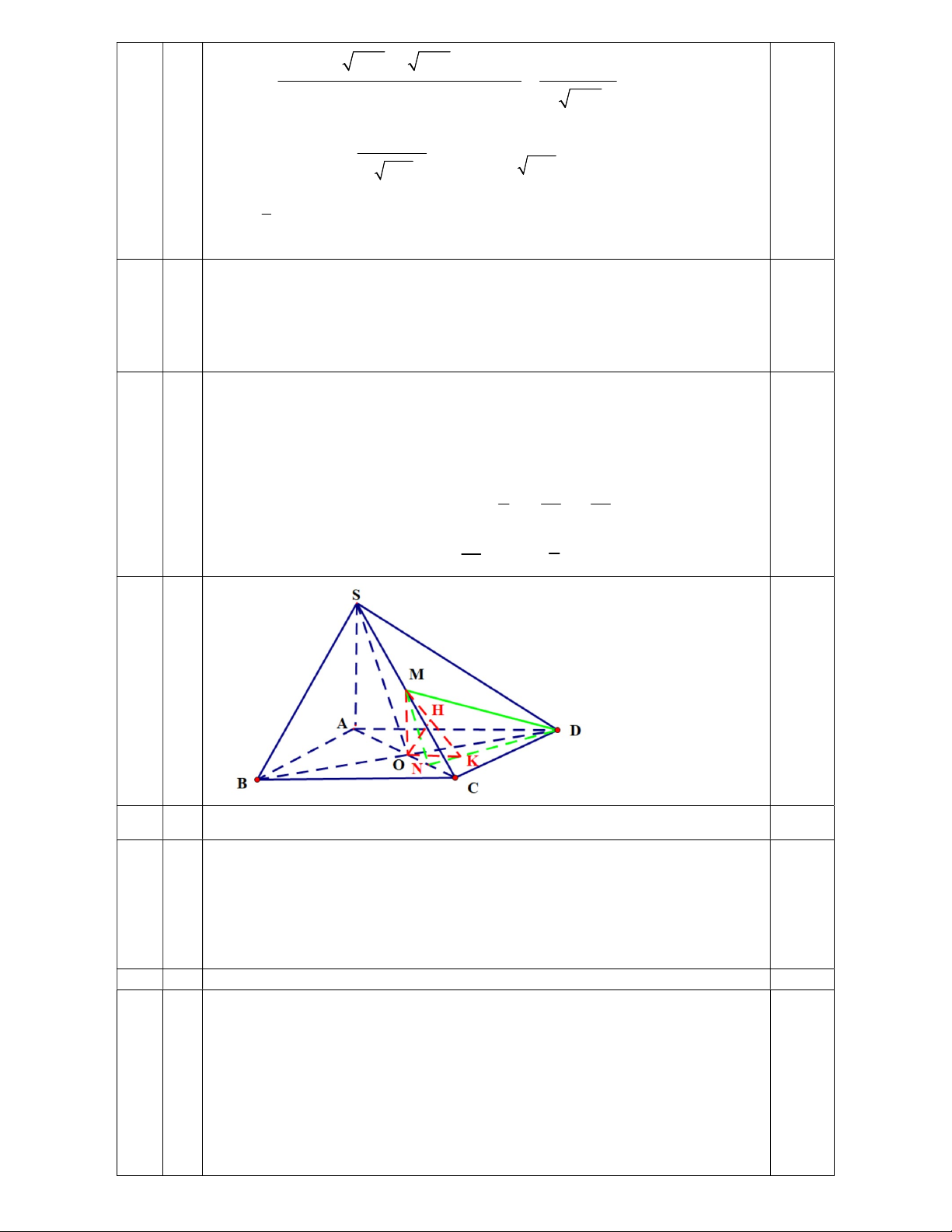
Vậy tổng hệ số góc nhỏ nhất bằng  khi m  4 4 6 a
Chứng minh : CD  SAD 0.75đ Ta có : 0.25 C  D  AD 0.25  C  D  SA  0.25 AD, SA   SAD, AD  SA  A  CD  SAD b
Chứng minh hai mặt phẳng (SAC) và (SBD) vuông góc với nhau Ta có : BD  AC 0.25  BD  SA  0.25 AH , SA   SAH , AH SA  A 0.25  BD  SAC  SBD  SAC c
Tính số đo của góc hợp bởi đường thẳng SO và mặt đáy (ABCD).
Hình chiếu của SO lên (ABCD) là AO 0.25  SO, 0.25   ABCD   SOA 
AC  AB 2  2a 2  AO  a 2 0.25  SA SOA    SO ABCD  0 tan 1 ,( )  45 AO d
Tính khoảng cách giữa hai đường thẳng SO và BM .
Kẻ MN // SO  SO / / BMN   d SO, BM   d O,BMN    0.25
Kẻ OK  BN,mà BN  MO ,  BN  (MNK)  (BMN)  (MOK) Mà (BMN )  (ONK )  MK
Kẻ OH  MK  OH  (BMN)   BM   d O BMN  M . O OK d SO, ,( )  OH  0.25 2 2 MO  OK ON.OB 2 SA a 2 Ta có OK   a; MO   2 2 ON  OB 10 2 2 0.25  d SO BM  2a 2 ,  3
SỞ GD & ĐT TP. HỒ CHÍ MINH Trường TH, THCS và THPT
ĐỀ KIỂM TRA HỌC KỲ II ( 2019 – 2020 ) TRƯƠNG VĨNH KÝ Môn: TOÁN – Khối: 11
Thời gian làm bài: 90 phút (Đề gồm 01 trang)
(Học sinh không được sử dụng tài liệu) Mã đề: B
Họ và tên học sinh: ............................................................................................................... Lớp: .........................
Số báo danh: .................................. Chữ ký học sinh: .......................................................... Ngày: 16/ 06/ 2020
Bài 1: (2 điểm). Tính đạo hàm các hàm số: 3x 1 a.) 3 2
y  3x  4x  2x 1 b.) y  x  2 c.) 2
y  5x  2x 1 d.) y  sin 4x  4 cos(4  x) 2 2x  5x  3  (khi x  3)
Bài 2: (1 điểm). Xét tính liên tục của hàm số: y  f (x)   x  3 tại điểm x  3. 0 3  x  2 (khi x  3) Bài 3: (2 điểm).
a.) Viết phương trình tiếp tuyến của đồ thị (C) hàm số: 4 2
y  x  3x  2 tại điểm thuộc đồ thị có hoành độ x  2  . 0 x  2
b.) Viết phương trình tiếp tuyến của đồ thị (C) hàm số: y  f (x) 
. Biết rằng tiếp tuyến song song x 1
với đường thẳng (d): y  3x  4 .
Bài 4 : (1 điểm). Cho hàm số f (x)  2x x 1 . Giải phương trình : 2. f  (  x)  3x  4 .
Bài 5: (1 điểm). Cho hàm số 3 2 2
y  f (x)  x  3mx  (2m 1)x  4m  3 có đồ thị là (C ) . Gọi k là hệ số góc m 1
của tiếp tuyến của đồ thị tại điểm có hoành độ bằng 0, gọi k là hệ số góc của tiếp tuyến của đồ thị tại 2
điểm có hoành độ bằng 1. Tìm m để tổng k  k đạt giá trị lớn nhất. 1 2
Bài 6: (3 điểm). Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh 4a và có tâm O. Cạnh bên
SA  2a 2 và vuông góc mặt đáy (ABCD) .
a.) Chứng minh: CB  (SAB) .
b.) Chứng minh hai mặt phẳng (SAC) và (SBD) vuông góc với nhau.
c.) Tính số đo của góc hợp bởi đường thẳng SO và mặt đáy (ABCD).
d.) Tính khoảng cách giữa hai đường thẳng SO và DM , với M là trung điểm SC.
----------------------- HẾT -----------------------
ĐÁP ÁN TOÁN 11 – KIỂM TRA HỌC KÌ 2 – 2019-2020 – ĐỀ B 1 a Tính đạo hàm a) 3 2 y  3x  4x  2x 1 / 2
y  6x  8x  2 ( đúng 2 số 0.25 ) 0.5 1 b 3x 1 Tính đạo hàm : y  x  2 3x  /
1  x  2   x  2/ 3x 1 0.25 /   y  x  22 0.25
3 x  2 13x   1 = 7 
(HS tính nhanh kq cho đủ điểm ) x  22 x  22 1 c) Tính đạo hàm 2 y  5x  2x 1 5x 2x  / 2 1 5x 1 / y   0.25x2 2 2 2 5x  2x 1 5x  2x 1 1 d)
Tính đạo hàm y  sin 4x  4cos 4  x y   x/ x    x/ / 4 cos 4 4 4
sin 4  x  4cos 4x  4sin 4  x 0.25x2 2 2x  5x  3 2  khi x  3
Xét tính liên tục y  f  x     x  3 tại điểm x  3 0 3  x  2  khi x  3 * f(3) = 7 (1) 0.25
* lim f  x  lim 3x  2  7 (2) 0.25 x 3 x 3   2 2x  5x  3 * lim f  x  lim  lim 2x   1  7 (3) 0.25 x 3 x 3  x 3 x 3     0.25
Từ (1) , (2) , (3) suy ra hàm số liên tục tại x  3 0 3 a
Viết phương trình tiếp tuyến của đồ thị ( C) hàm số : 4 2
y  x  3x  2 tại điểm
thuộc đồ thị có hoành độ x  2 0 * / 3 y  4x  6x 0.25 * Hệ số góc k = - 20 0.25 * Tiếp điểm  2  ;6 0.25 0.25
PT Tiếp tuyến : y  6  2  0x  2  y  2  0x 34 3 b x 
Viết phương trình tiếp tuyến của đồ thị ( C) hàm số : y  f  x 2  .Biết x 1
rằng tiếp tuyến song song với đường thẳng (d) : y  3x  4 3  0.25 * / y  x  2 1 3  x  0
*Hệ số góc tiếp tuyến k 0 0.25 tt = kd = - 3   3     x  2 1 x  2  0 0 0.25
*Tiếp điểm (0;-2)  PT Tiếp tuyến :y = -3x -2 0.25
*Tiếp điểm ( 2 ;4)  PT Tiếp tuyến :y = - 3x + 10 4
Cho f  x  2x x 1 . Giải phương trình : // 2. f  x  3x  4     x  0.25 f x
2x x 1   x 1/ / 3 2 / 2x  x 1  0.25 3x  2 x 1  x 1 3x  2 3x  4 //  / /   f  x   x 1 2 x 13 3  x4  0 3x 4 0.25 // 2.f x  3x4  2.      ,điều kiện x > 1   3x 4  x x   3 3 1 1 2 1  4 x  (nh)   0,25 3  x  2 (nh) 5 Cho hàm số y  f  x 3 2  x  mx   2 3 2m  
1 x  4m  3 có đồ thị là C . m 
Gọi k là hệ số góc của tiếp tuyến của đồ thị tại điểm có hoành độ bằng 0,gọi 1
k là hệ số góc của tiếp tuyến của đồ thị tại điểm có hoành độ bằng 1.Tìm m 2
để tổng k  k đạt giá trị lớn nhất ? 1 2 / 2 2
y  3x  6mx  2m 1 0.25 Ta có: 2 k  f '(0)  2  m 1 0.25 1 2 k  f '(1)  2  m  6m  4 2 2  3  29 29 0.25x2 Ta có: 2
k  k  4m  6m  5  4  m     1 2    4  4 4 29 3
Vậy tổng hệ số góc lớn nhất bằng  khi m  4 4 6 a
Chứng minh : CB  SAB . Ta có : CB  AB 0.25  0.25   CB SA  AB, SA   SAB, AB  SA  A 0.25  CB  SAB b
Chứng minh hai mặt phẳng (SAC) và (SBD) vuông góc với nhau . Ta có : BD  AC 0.25  BD  SA  AH , SA   SAH , AH SA  A 0.25  BD  SAC 0.25  SBD  SAC c
Tính số đo của góc hợp bởi đường thẳng SO và mặt đáy (ABCD).
Hình chiếu của SO lên (ABCD) là AO 0.25  SO,   ABCD   SOA c  0.25
AC  AB 2  2a 2  AO  a 2 0.25  SA SOA    SO ABCD  0 tan 1 ,( )  45 AC d
Tính khoảng cách giữa hai đường thẳng SO và DM .
Kẻ MN // SO  SO / / DMN   d SO, DM   d O,DMN    0.25
Kẻ OK  BN,mà BN  MO ,  DN  (MNK)  (DMN)  (MOK) Mà (DMN )  (ONK)  MK d
Kẻ OH  MK  OH  (DMN)   DM   d O DMN  M . O OK d SO, ,( )  OH  2 2 MO  OK 0.25 ON.OB 4 SA Ta có OK   a; MO   a 2 2 2 ON  OB 10 2 0.25  d SO BM  4a 2 ,  3