UBND HUYỆN BÌNH CHÁNH
ĐỀ KIỂM TRA HỌC KỲ II TRƯỜNG THCS ĐỒNG ĐEN NĂM HỌC 2019 - 2020 MÔN: TOÁN 9 Đ Ề C H Í N H T HỨ C
Ngày kiểm tra: ngày 17 tháng 6 năm 2020
Thời gian làm bài bài: 90 phút (không kể thời gian phát đề)
(Đề kiểm tra có 02 trang)
Bài 1. (2,0 điểm) Giải các phương trình sau. a) 2 x  4x  5  0 b)  2 5 x   1  3  7x Bài 2. (1,5 điểm) 1 Cho Parabol (P): 2
y   x và đường thẳng (D): y  x  4 2
a) Vẽ (P) và (D) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép tính. Bài 3. (1,0 điểm) Cho phương trình: 2
x 8x  3  0 có 2 nghiệm là x ; x . Không giải phương trình, hãy 1 2
tính giá trị của biểu thức A  4x  4x 11x x 1 2 1 2 Bài 4. (1,0 điểm)
Ở nước ta và nhiều nước khác, nhiệt độ được tính theo độ C ( C là chữ cái đầu tên của nhà
thiên văn học người Thụy sĩ Celsius ). Còn ở Anh và Mỹ nhiệt độ được tính theo độ F ( F là chữ
cái đầu tên của nhà vật lý học người Đức Fahrenheit). Công thức chuyển đổi từ độ F sang độ C như sau: F  aC  32
a) Tính a biết khi nhiệt độ phòng là 250C thì trên điều khiển của máy điều hòa là 770F
b) Nhiệt độ của bạn An là 1020F. Bạn An có sốt không? Biết nhiệt độ cơ thể người trên 370C là sốt. Bài 5. (1,0 điểm)
Đầu năm học, một trường THCS tuyển được 75 học sinh vào 2 lớp chuyên toán và chuyên 8
văn. Nếu chuyển 15 học sinh từ lớp Toán sang lớp Văn thì số học sinh lớp Văn bằng số học 7
sinh lớp Toán. Hãy tìm số học sinh của mỗi lớp Bài 6. (1,0 điểm)
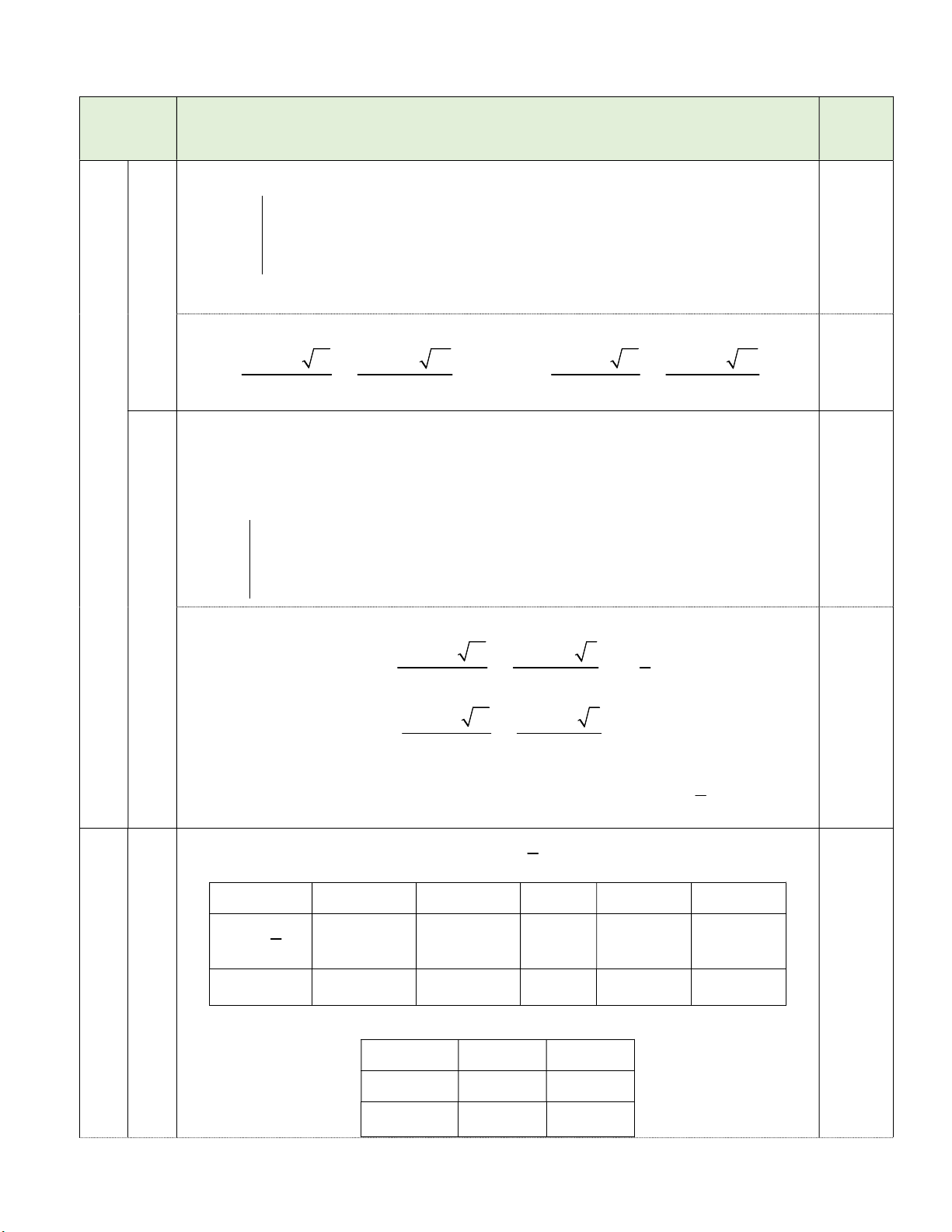
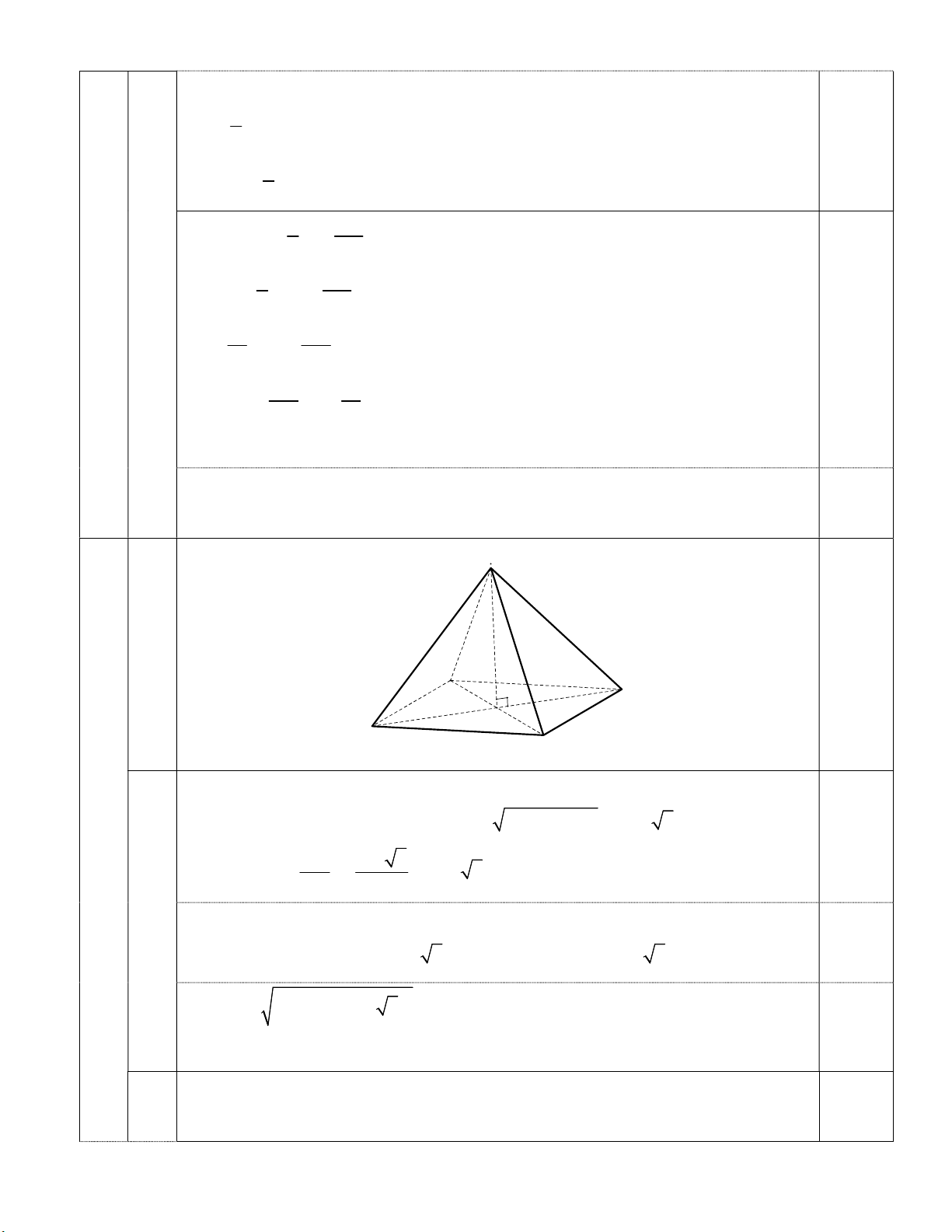
Kim tự tháp Kheops – Ai Cập có dạng hình chóp đều, đáy là hình vuông, các mặt bên là các
tam giác cân chung đỉnh (hình vẽ). Mỗi cạnh bên của kim tự tháp dài 214m, cạnh đáy của nó dài 230m.
a) Tính theo mét chiều cao h của kim tự tháp (làm tròn đến chữ số thập phân thứ nhất). 1
b) Cho biết thể tích của hình chóp được tính theo công thức V  S.h , trong đó S là diện 3
tích đáy, h là chiều cao của hình chóp. Tính theo m3 thể tích của kim tự tháp này
(làm tròn đến hàng nghìn). S 214 m h A D O B 230 m C Bài 7. (2,5 điểm)
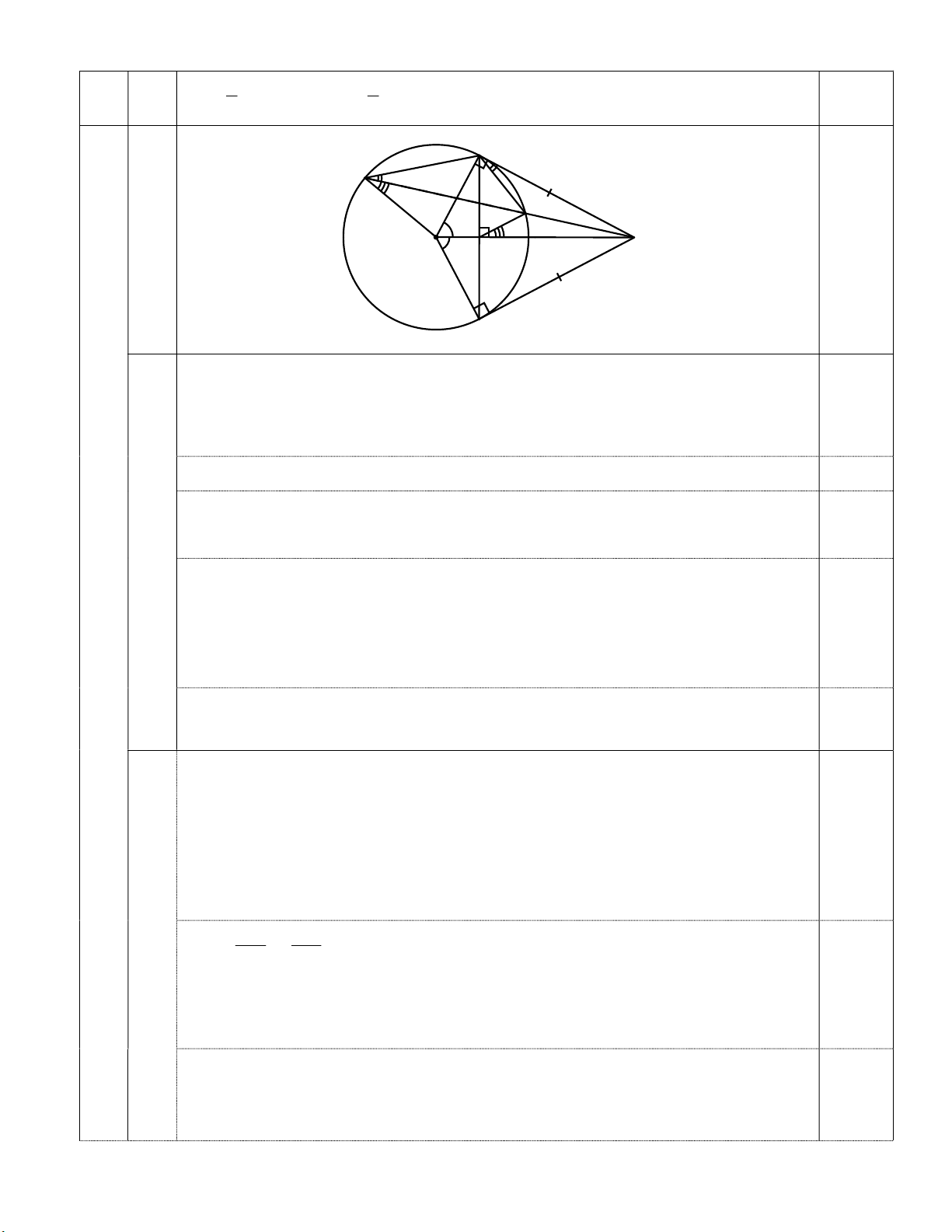
Cho đường tròn ( O, R ) và điểm A nằm ngoài ( O ). Từ A vẽ 2 tiếp tuyến AB; AC và cát
tuyến AED với ( O ) ( B; C là 2 tiếp điểm, E nằm giữa A và D).
a) Chứng minh tứ giác ABOC nội tiếp và OA  BC tại H. b) Chứng minh 2
AC  AE.AD . Từ đó suy ra tứ giác OHED nội tiếp
…………………… HẾT……………………
(Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh: ………………………………………… Số báo danh: …………..
ĐÁP ÁN ĐỀ THI HỌC KÌ 2 MÔN TOÁN 9, NĂM HỌC 2019 – 2020 Biểu Bài Nội dung điểm 2 x  4x  5  0  a  1 0,25 +  b  4     2
b  4ac   2 4  4.  1 .  5  36  0 0,25  c  5 a
Vậy phương trình có hai nghiệm phân biệt: 0,25 +   b     4  36   b     4  36 x    1;    x    5  1 0,25 2.a 2.  1 2 2.a 2.  1  2 5 x   1  3 7x ) m 2
 5x  5 3  7x  0 iể 2
 5x  7x  2  0   1 0,25 + 1(2 đ  a  5 0,25  b  7     2
b  4ac   2 7  4.  5 .  2  9  0  c  2 b
Vậy phương trình (1) có hai nghiệm phân biệt:   b     7  9 2  x     1 2.a 2.  5 5 0,25 +   b     7  9  x    1  0,25 2 2.a 2.  5 Kết luận: V  
ậy tập nghiệm của phương trình đã cho là 2 S  1;       .  5   1
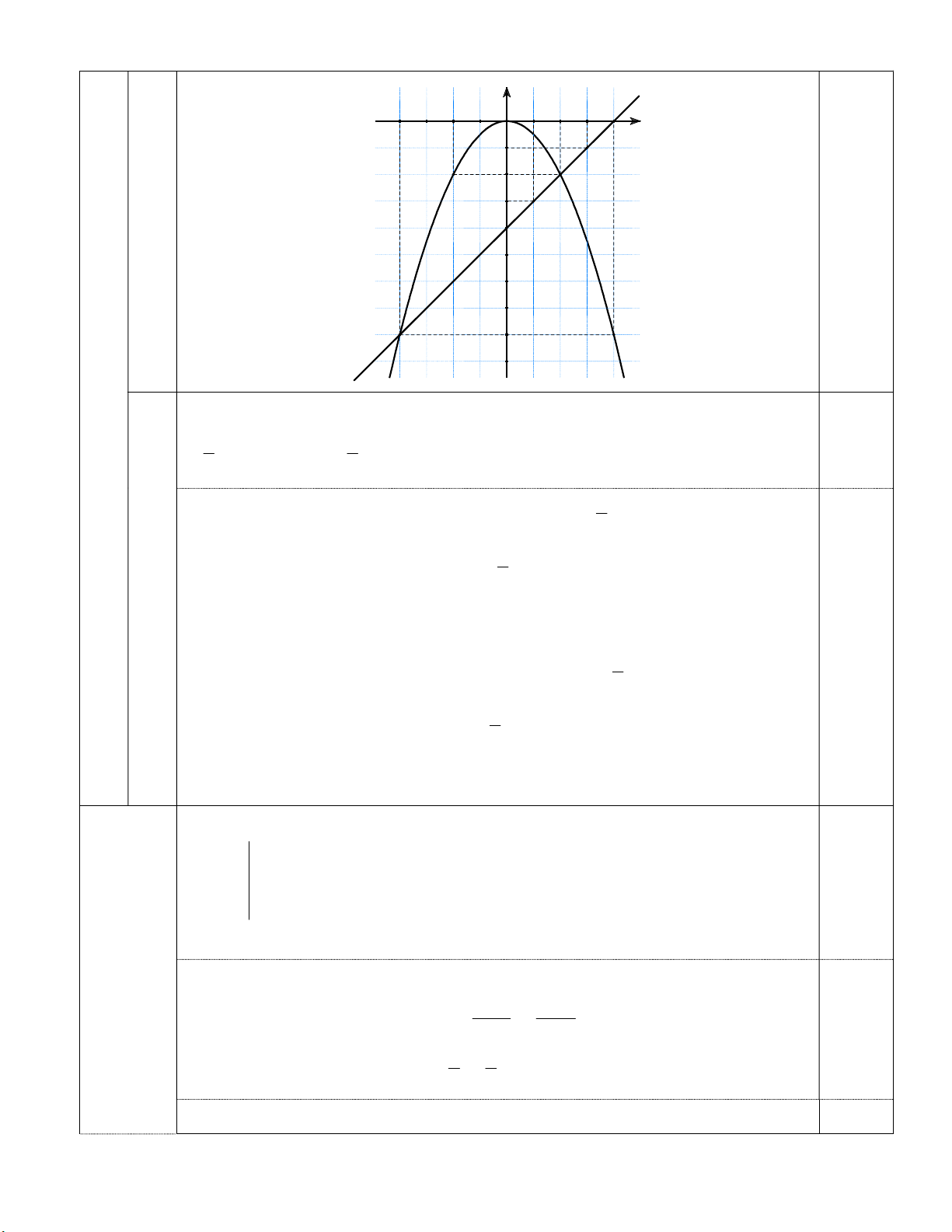
 Lập bảng giá trị cho hàm số P 2 : y   x 2 x 4  2  0 2 4 ) 1 2 m y   x 8  2  0 2  8  iể 2 0,25 + a Tọa độ A 4;  8 B 2;  2 O 0;  0 B 2;  2 A4;  8 0,25 2 (1,5 đ
 Lập bảng giá trị cho hàm số D : y  x  4 x 3 1 y  x  4 1 3  Tọa độ C 3;  1 D 1;  3 y -4 -2 O 1 2 3 4 x -1 C B -2 B' -3 D 0,5 A A' (D) -8 (P)
 Phương trình hoành độ giao điểm của P và D là: 1 1  x  2 2  x  x  4 2
  x  x  4  0   1 1    0,25 2 2  x  4 2  1
 Với x  x  2, thay vào công thức P 2 : y   x ta được: 1 2 1 y    2 2  2  2 b
Vậy tọa độ giao điểm thứ nhất là B2;  2 0,25 1
 Với x  x  4 , thay vào công thức P 2 : y   x ta được: 2 2 1 y    2 4  8  2
Vậy tọa độ giao điểm thứ nhất là A 4;  8 Xét phương trình 2 x  8x  3  0, ta có:  a  1
 b  8     2
b  ac   2 4 8  4.  1 .  3  52  0 0,25  c  3 3
Vậy phương trình luôn có hai nghiệm phân biệt. (1,0
Theo hệ thức của định lý Vi-ét, ta có: điểm)    b   8  x   x    8  1 2  a 1 0,25   c 3  x x    3 1 2  a 1
Từ hệ thức của đề bài A  4x  4x 11x x 0,25 1 2 1 2
 A  4x  x 11 x x 1 2   1 2  A  4.  8 11.  3 0,25  A  6  5
Theo đề bài ta có: C  25 và F  77 .
Thay C  25 và F  77 vào công thức F  . aC  32, ta được: 0,25 77  . a 2  5  32  77  25a  32   25a  32 77 a  2  5a  4  5 45  a  25 9  a  5
Khi đó công thức chuyển đổi từ độ F sang độ C là: 9 F  C  32 0,25 ) 5 m iể
Thay F  102 vào công thức 9 F  C  32, ta được: 5 0,25 9 4 (1,0 đ 102  C  32 5 9   C  32102 5 9   C  7  0 5 b 70  C  9  5 70  C  9  5  C  38,8
Như vậy bạn An bị sốt vì 38, 8 C   37 C  . 0,25
Gọi x HS là số học sinh của đội tuyển chuyên Toán lúc đầu. Điều kiện: x nguyên ) m dương, x  75. iể
Số học sinh chuyên Văn lúc đầu là: 75 xHS 0,25 5 (1,0 đ
Số học sinh chuyên Toán lúc sau là: x 1  5 HS
Số học sinh chuyên Văn lúc sau là: 75 x  15  90 xHS
Vì sau khi chuyển 15 học sinh từ lớp Toán sang lớp Văn thì số học sinh lớp Văn
bằng 8 số học sinh lớp Toán, ta có phương trình: 7 0,25 8 90  x  x 1  5 7 8 120  90 x  x  7 7 8 120  x   x    90 7 7 15 750   x   7 7 0,25  750  15  x    :          7   7   x  50nhËn
Kết luận: Vậy số học sinh ở lớp chuyên Toán lúc đầu là 50HS, chuyên Văn là 0,25 75  50  25HS S 214m ình h H A D O B 230m C ) Xét C  BD vuông tại C , có: 2 2 2
BD  CB CD (định lí Py-ta-go) m iể Thay số: 2 2 2 BD  230  230 2 2
 BD  230  230  230 2m 0,25 BD 230 2 6 (1,0 đ Suy ra: OD    115 2m 2 2 a Xét S  OD vuông tại C , có: 2 2 2
SD  SO OD (định lí Py-ta-go) 0,25
Thay số:    SO   2 2 2 214 115 2  SO     2 2 2 214 115 2  SO     2 2 214 115 2  139,  1  m 0,25
Kết luận: Vậy h  SO  139,  1  m
 Diện tích mặt đáy ABCD của Kim tự tháp là: b S  BC   2 2   2 230
52 900 m (ABCD là hình vuông) 0,25 ABCD  1 V  S h     m ABCD 
1 52 900 139,1 2 453 000 3 3 3 B D E ình A H O H C Ta có:
AB  OB tại B (AB là tiếp tuyến của O tại B (gt)) 0,25
AC  OC tại C (AC là tiếp tuyến của O tại C (gt)) Suy ra:  ABO   ACO  90 0,25 Xét tứ giác ABOC có:  ABO 
 ACO  90  90  180 . 0,25 0,25
a Vậy tứ giác ABOC nội tiếp được đường tròn.(Dấu hiệu 2).
 Chứng minh: OA  BC tại H . ) m Ta có: iể
AB  AC (AB, AC là hai tiếp tuyến của O cắt nhau tại A (gt)). 0,25 7 (2,5 đ
OB  OC  R (cùng bằng bán kính của O(gt))
Suy ra: OA là đường trung trực của BC . 0,25
Do đó: OA  BC tại H và H là trung điểm của BC .
Nối E với C và D với C . Xét A  BE và A  DB có:   ABE 
 ADB (cùng chắn cung BE của O)   A chung 0,25
Suy ra: ABE ∽ ADB g.g b Do đó: AB AE  tslg 2  AB  AE.AD AD AB
Ta lại có: AB  AC cmt 0,25 Do đó: 2 AC  AE.AD đpc  m
 Chứng minh: Tứ giác OHED nội tiếp.
Ta có: BH  OA tại H (OA  BC tại H (cmt).
Do đó BH là đường cao của A  BO . Ta lại có: A  BO vuông tại B (  ABO  90cmt) Suy ra: 2
AB  AH.AO (hệ thức lượng) Mặt khác: 2 AB  AE.AD cmt Do đó: AH.AO  AH AE AE.AD   AD AO 0,25 Xét A  HE và A  DO có:   A chung    AHE ∽ ADO AH AE c.g.c   cmt AD AO  Do đó:  AHE 
 ADO (hai góc tương ứng)
Vậy tứ giác OHED nội tiếp được đường tròn.(Dấu hiệu 4). 0,25