Đề thi học kì 2 Toán 9 năm 2023 – 2024 phòng GD&ĐT Thạch Thất – Hà Nội
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề kiểm tra cuối học kì 2 môn Toán 9 năm học 2023 – 2024 phòng Giáo dục và Đào tạo huyện Thạch Thất, thành phố Hà Nội; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!
Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
BÀI KIỂM TRA HỌC KÌ II THẠCH THẤT
Năm học: 2023 – 2024 MÔN: TOÁN LỚP 9
Họ và tên:……………………………..
(Thời gian: 90 phút không kể thời gian giao đề)
Lớp:……Trường:……………………..
(Bài kiểm tra gồm 04 trang) Điểm
Lời phê của thầy, cô giáo
(Học sinh làm trực tiếp vào bài kiểm tra này) Bài I. + −
(2,5 điểm): Cho hai biểu thức: x 3 x 1 A = + và x 5 B =
với x ≥ 0;x ≠ 25 . x − 25 x + 5 x + 2
1) Tính giá trị của biểu thức B khi x = 9;
2) Rút gọn biểu thức P = . A ; B
3) Tìm các giá trị của x để 1 P > . 3
Bài II. (2,0 điểm): Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Một cơ sở dệt theo kế hoạch phải dệt 600 tấm thảm trong một thời gian quy định. Khi
thực hiện mỗi ngày cơ sở dệt đã dệt được nhiều hơn dự định 6 tấm thảm, vì vậy 1 ngày trước
khi hết thời gian quy định cơ sở dệt không những hoàn thành kế hoạch mà còn dệt thêm được
44 tấm thảm. Hỏi theo kế hoạch mỗi ngày cơ sở đó dệt bao nhiêu tấm thảm?
Bài III. (2,0 điểm): 3 x − y = 7
1. Giải hệ phương trình sau: x + 3y = 9 2. Cho phương trình 2
x − 2(m + )
1 x + 2m +1= 0 (1) với x là ẩn số, m là tham số.
a) Giải phương trình khi m = 2.
b) Tìm các giá trị của m để phương trình (1) có 2 nghiệm phân biệt x 1 1 1, x2 thoả mãn + = 3. x x 1 2
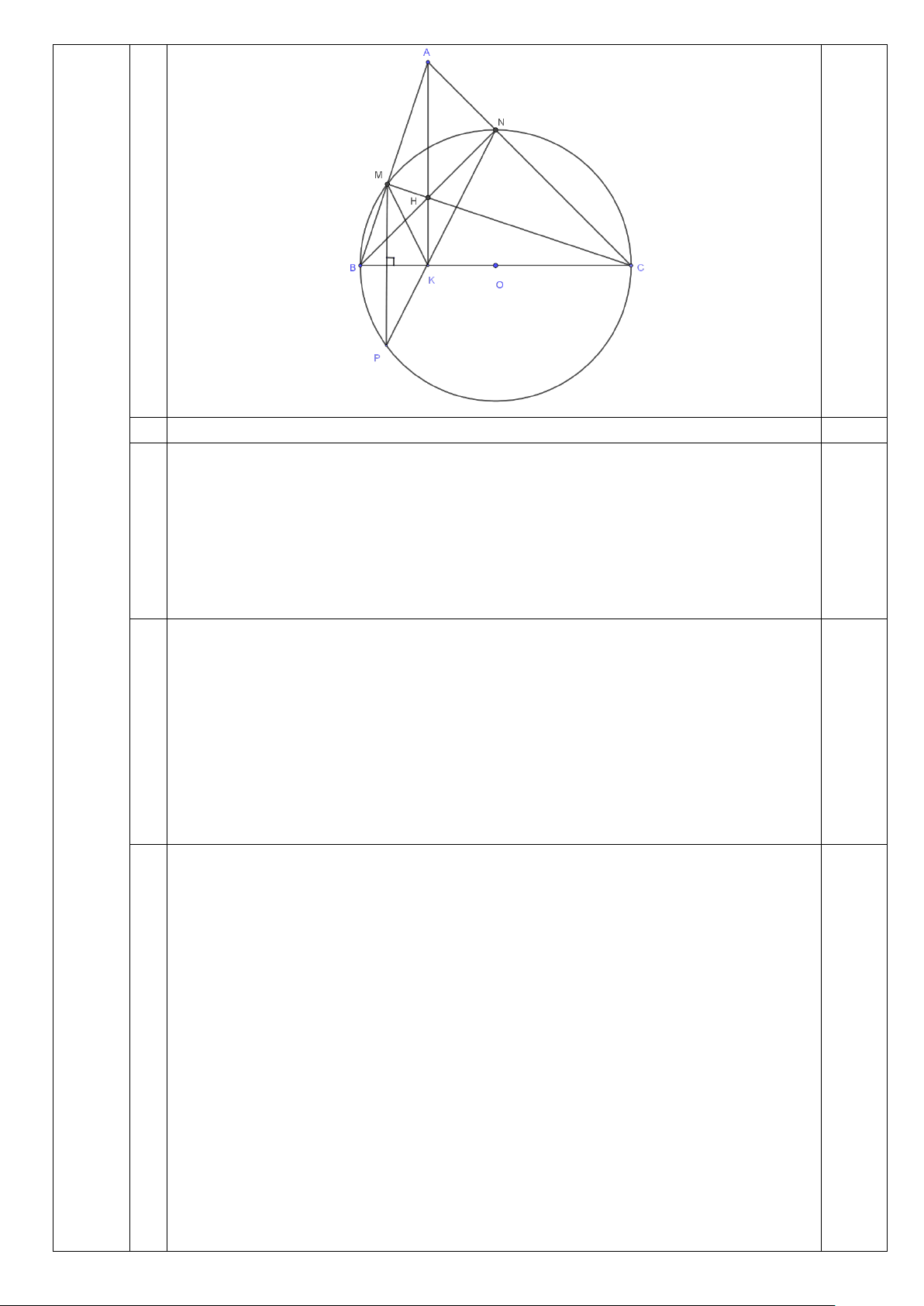
Bàì IV. (3,0 điểm): Cho tam giác nhọn ABC vẽ đường tròn đường kính BC cắt các cạnh AB,
AC lần lượt tại M và N. Gọi H là giao điểm của BN và CM
a) Chứng minh tứ giác AMHN nội tiếp được trong một đường tròn.
b) Gọi K là giao điểm của BC với AH. Chứng minh ∆BHK đồng dạng với ∆ACK.
c) Chứng minh: KM + KN ≤ BC. Dấu " = " xảy ra khi nào?
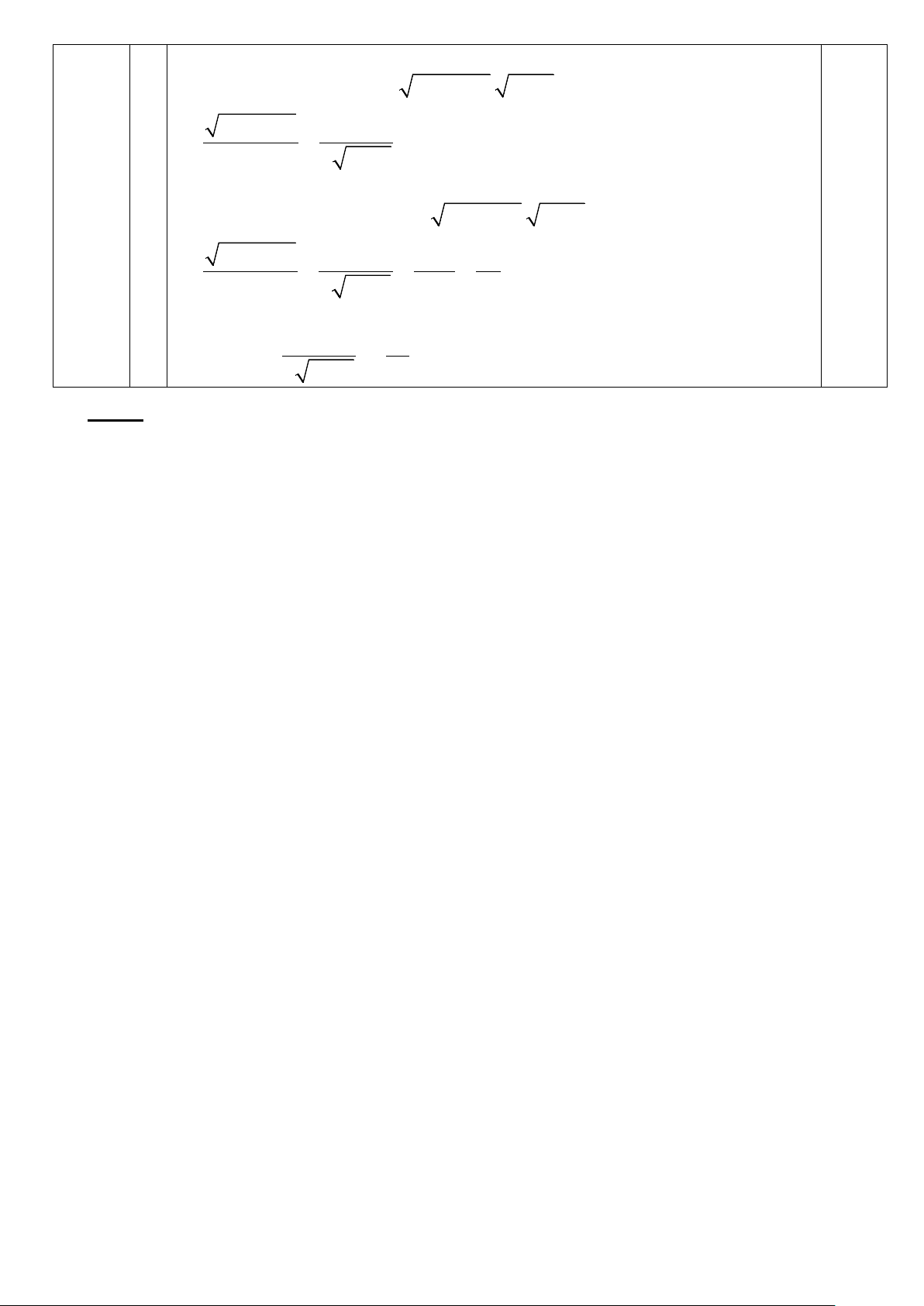
Bài V. (0,5 điểm): Tìm giá trị lớn nhất của biểu thức: x − 2023 x − 2024 A = + với x > 2024. x + 2 x Bài làm 1 2 3 4
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN, BIỂU ĐIỂM CHẤM THẠCH THẤT
BÀI KIỂM TRA HỌC KÌ II
Năm học: 2023 - 2024
(Hướng dẫn chấm gồm 04 trang) MÔN: TOÁN - LỚP 9 Bài Ý Đáp án Điểm x + x x − Cho hai biểu thức: 3 1 A = + và 5 B = x − 25 x + 5 x + 2
với x ≥ 0;x ≠ 25
Thay x = 9 (TMĐK) vào biểu thức B ta được: 1 9 5 3 5 2 0,5 B − − = = = − 9 + 2 3 + 2 5 + Rút gọn x 3 x 1 x −5 P = . A B = + .
với x ≥ 0;x ≠ 25 x − 25 x + 5 x + 2 0,5 x + x x − x − = 3 5 5 + .
( x − 5)( x + 5) ( x −5)( x + 5) x + 2 = x + 4 x −5 x −5 . 0,25 2
( x −5)( x +5) x + 2 I x − x + x − (2,5 đ) = ( 1)( 5) 5 .
( x −5)( x +5) x + 2 0,5 = ( x −1) ( x + 2) 0,25 Ta có 1 P > x −1 1 ⇔ > x −1 1 ⇔ − > 0 3 x + 2 3 x + 2 3
3 x −3− x − 2 ⇔ > 0 3( x + 2) 0,25 2 x −5 ⇔ > 0 3 3( x + 2)
Vì x ≥ 0 nên x + 2 > 0 ⇒ 3( x + 2) > 0. Do đó 5
2 x −5 > 0 ⇔ x > 2 0,25 Suy ra 25 x > P > ⇔ > 4 . Vậy 1 25 x và x ≠ 25. 3 4
Gọi số tấm thảm cơ sở dệt phải dệt trong 1 ngày theo kế hoạch là x (tấm) 0,25 Điều kiện *
x∈ N , x < 600. 0,25
Thời gian dệt theo kế hoạch là: 600 (ngày) x 0,25
Số tấm thảm dệt trong 1 ngày trên thực tế là: x+6 (tấm) 1
Thời gian dệt theo thực tế là: 644 (ngày) 0,25 x + 6
Vì một ngày trước khi hết thời gian dự định cơ sở dệt không những hoàn
thành kế hoạch mà còn dệt thêm được 44 tấm thảm nên ta có phương II 0,25 − =
(2,0đ) 1 trình: 600 644 1 x x + 6 x = 40(TM )
Giải phương trình ta được: 1 0,5 x = 90 − (KTM ) 2 0,25
Vậy theo kế hoạch mỗi ngày cơ sở dệt phải dệt được 40 tấm thảm. 3 x − y = 7
Giải hệ phương trình sau: x + 3y = 9 = − = − = − = y 3x 7 y 3x 7 y 3x 7 x 3 ⇔ ⇔ ⇔ ⇔ x 3(3x 7) 9 x 9x 21 9 10 x 30 + − = + − = = y = 2 1
KL: Vậy hệ phương trình có nghiệm duy nhất là: ( ; x y) = (3;2)
Cách 2: Giải bằng phương pháp cộng đại số tìm x, y … Cho phương trình 2
x − 2(m + ) 1 x + 2m +1= 0
a) Giải phương trình khi m = 2
Khi m = 2 phương trình có dạng 2
x − 6x + 5 = 0 0,5
2 Giải PT tìm được nghiệm x =1; x = 5 1 2
b) Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt x ;x 1 2 thoả mãn 1 1 + = 3 III x x 1 2 (2,0đ) Tính được: 2 ∆ = m
Lập luận: Để phương trình có 2 nghiệm phân biệt ⇔ ∆ > 0 ⇔ m ≠ 0
x + x = 2(m +1) 0,25 Theo Viet ta có 1 2 x x = 2m + 1 1 2 Theo đề bài ta có: 1 1 + = 3 x x 1 2 1 1
x + x − 3x x 1 2 1 2 + = 3 ⇔ = 0 x x x x 1 2 1 2
2(m +1) − 3(2m +1) 1 0 (m − ⇔ = ≠ ) 0,25 2m +1 2 1 4m 1 0 m − ⇒ − − = ⇔ = (thỏa mãn) 4 Vậy 1 m − = là giá trị cần tìm. 4 2
Vẽ hình đúng đến câu a 0,25
a) Theo giả thiết ta có = 0
BMC BNC = 90 (góc nội tiếp chắn nửa đường tròn) ⇒ = = 90o AMH ANH 0,5
1 Xét tứ giác AMHN có ⇒ AMH + o 0 0 ANH = 90 + 90 =180
Mà 2 góc này ở vị trí đối nhau
⇒Tứ giác AMHN nội tiếp đường tròn. 0,5 IV
Vì BN ⊥ AC , CM ⊥ AB ⇒ H là trực tâm A ∆ BC . (3,0 đ)
⇒ AK ⊥ BC ⇒ AKB = 0 ANB = 90 .
Suy ra tứ giác ABKN nội tiếp đường tròn. 0,5 2 ⇒ =
KAC NBC (cùng chắn KN ) Xét B ∆ HK và A ∆ CK có: =
HBK KAC (c/m trên) ; = 0 HKB AKC = 90 0,5 B
∆ HK đồng dạng A ∆ CK (g-g)
Từ M kẻ đường thẳng vuông góc với BC cắt đường tròn tâm O tại P
⇒ BC là trung trực của MP (tính chất đối xứng của đường tròn) ⇒ KM = KP
Ta có tứ giác ABKN nội tiếp (c/m câu b) ⇒ = ABN AKN
c/m tứ giác BMHK nội tiếp⇒ = ABN HKM 0,25 Suy ra = AKN HKM 3 ⇒ MKB =
NKC (cùng phụ với hai góc bằng nhau)
Mặt khác BC là trung trực của MP nên = ⇒ = MKB BKP BKP NKC
⇒ 3 điểm P, N,K thẳng hàng 0,25
suy ra KM + KN = KP + KN = PN ≤ BC (do PN là dây còn BC là đường kính).
Dấu “=” xảy ra khi K trùng với tâm O của đường tròn đường kính BC , 0,25 khi đó A
∆ BC cân tại A. 3 Vận dụng BĐT Cô-si
x = (x − 2024) + 2024 ≥ 2 x − 2024. 2024 x − 2024 1 ⇒ ≤ x 2 2024
Dấu “=” xảy ra khi x − 2024 = 2024 ⇔ x = 4048 (TMĐK) V 0,25
(0,5đ) x + 2 = (x − 2023) + 2025 ≥ 2 x − 2023. 2025 x − 2023 1 1 1 ⇒ ≤ = = x + 2 2 2025 2.45 90
Dấu “=” xảy ra khi x − 2023 = 2025 ⇔ x = 4048(TMĐK) 0,25 Vậy Amax = 1
+ 1 tại x = 4048 2 2024 90
Lưu ý: - Học sinh làm cách khác đúng vẫn cho điểm tối đa;
- Điểm toàn bài làm tròn đến 0,5 điểm./.
--------------------- Hết ----------------------- 4
Document Outline
- BÀI KIỂM TRA HK II TOÁN 9
- Hướng dẫn chấm Toán 9 HKII (2023-2024)